Hostname: page-component-784d4fb959-57n77 Total loading time: 0 Render date: 2025-07-17T03:47:29.877Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Insolubility of a Class of Diophantine Equations and the Nontriviality of the Class Numbers of Related Real Quadratic Fields of Richaud-Degert Type

Published online by Cambridge University Press:  22 January 2016

R. A. Mollin
R. A. Mollin*
Affiliation:
Mathematics Department University of Calgary, Calgary, Alberta T2N 1N4, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Many authors have studied the relationship between nontrivial class numbers h(n) of real quadratic fields 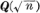and the lack of integer solutions for certain diophantine equations. Most such results have pertained to positive square-free integers of the form n = l2 + r with integer >0, integer r dividing 4l and — l<r<l. For n of this form, 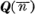is said to be of Richaud-Degert (R-D) type (see [3] and [8]; as well as [2], [6], [7], [12] and [13] for extensions and generalizations of R-D types.)

Information

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 105 , March 1987 , pp. 39 - 47
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1987

References

[ 1 ] Ankeny, N. C. Chowla, S. and Hasse, H., On the class number of the real subfield of a cyclotomic field, J. reine angew. Math., 217 (1965), 217–220.CrossRefGoogle Scholar
[ 2 ] Azuhata, T., On the fundamental units and the class numbers of real quadratic fields, Nagoya Math. J., 95 (1984), 125–135.Google Scholar
[ 3 ] Degert, G., Uber die Bestimmung der Grundeinheit gewisser reell-quadratischer Zahlkorper, Abh. Math. Sem. Univ. Hamburg, 22 (1958), 92–97.Google Scholar
[ 4 ] Hasse, H., Uber mehrklassige aber eingeschlechtige reell-quadratische Zahlkörper, Elem. Math., 20 (1965), 49–59.Google Scholar
[ 5 ] Lang, S. D., Note on the class-number of the maximal real subfield of a cyclotomic field, J. reine angew Math., 290 (1977), 70–72.Google Scholar
[ 6 ] Mollin, R. A., Lower Bounds for class Numbers of Real Quadratic Fields, Proc. Amer. Math. Soc, 96 (1986), 545–550.Google Scholar
[7] Mollin, R. A., Diophantine equations and class numbers, J. Number Theory, 24 (1986), 7–19.CrossRefGoogle Scholar
[ 8 ] Richaud, C., Sur la résolution des équationsx2 — Ay2 — ± 1, Atti Accad. pontif. Nuovi Lincei (1866), 177–182.Google Scholar
[ 9 ] Takeuchi, H., On the class-number of the maximal real subfield of a cyclotomic field, Canad. J. Math., 33(1) (1981), 55–58.Google Scholar
[10] Wada, H., A Table of Ideal Class Numbers of Real Quadratic Fields, Kôkyûroku in Math., 10 (1981), Sophia University, Tokyo.Google Scholar
[11] Yokoi, H., On the diophantine equation x2 — py2 = ± 4q and the class number of real subfields of a cyclotomic field, Nagoya Math. J., 91 (1983), 151–161.Google Scholar
[12] Yokoi, H., On real quadratic fields containing units with norm — 1, Nagoya Math. J., 33 (1968), 139–152.Google Scholar
[13] Yokoi, H., On the fundamental unit of real quadratic fields with norm 1, J. Number Theory, 2 (1970), 106–115.Google Scholar