Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
MITOMA, Itaru
1981.
MARTINGALES OF RANDOM DISTRIBUTIONS.
Memoirs of the Faculty of Science, Kyushu University. Series A, Mathematics,
Vol. 35,
Issue. 1,
p.
185.
Gorostiza, Luis G.
1982.
Advances in Filtering and Optimal Stochastic Control.
Vol. 42,
Issue. ,
p.
142.
Mitoma, Itaru
1983.
Probability Theory and Mathematical Statistics.
Vol. 1021,
Issue. ,
p.
446.
Mitoma, Itaru
1983.
Continuity of stochastic processes with values in the dual of a nuclear space.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 63,
Issue. 2,
p.
271.
Dawson, Donald A.
and
Gorostiza, Luis G.
1984.
Limit Theorems for Supercritical Branching Random Fields.
Mathematische Nachrichten,
Vol. 118,
Issue. 1,
p.
19.
Gorostiza, Luis G.
1984.
Stochastic Differential Systems Filtering and Control.
Vol. 69,
Issue. ,
p.
91.
Mitoma, Itaru
1985.
An ∞-dimensional inhomogeneous Langevin's equation.
Journal of Functional Analysis,
Vol. 61,
Issue. 3,
p.
342.
Mitoma, Itaru
1987.
Generalized ornstein-uhlenbeck process having a characteristic operator with polynomial coefficients.
Probability Theory and Related Fields,
Vol. 76,
Issue. 4,
p.
533.
Kallianpur, G.
and
Perez-Abreu, V.
1988.
Stochastic evolution equations driven by nuclear-space-valued martingales.
Applied Mathematics & Optimization,
Vol. 17,
Issue. 1,
p.
237.
Gorostiza, Luis G
1988.
The demographic variation process of branching random fields.
Journal of Multivariate Analysis,
Vol. 25,
Issue. 2,
p.
174.
Gorostiza, Luis G.
1988.
Limit theorems for supercritical branching random fields with immigration.
Advances in Applied Mathematics,
Vol. 9,
Issue. 1,
p.
56.
Swindle, Glen
1990.
A mean field limit of the contact process with large range.
Probability Theory and Related Fields,
Vol. 85,
Issue. 2,
p.
261.
Fernández, Begoña
1990.
Markov properties of the fluctuation limit of a particle system.
Journal of Mathematical Analysis and Applications,
Vol. 149,
Issue. 1,
p.
160.
Dawson, Donald A.
and
Gorostiza, Luis G.
1990.
Generalized solutions of a class of nuclear-space-valued stochastic evolution equations.
Applied Mathematics & Optimization,
Vol. 22,
Issue. 1,
p.
241.
Fernández, Begoña
1991.
Markov properties of the fluctuation limit of a particle system with death.
Journal of Mathematical Analysis and Applications,
Vol. 155,
Issue. 1,
p.
66.
López-Mimbela, J.Alfredo
1992.
Fluctuation limits of multitype branching random fields.
Journal of Multivariate Analysis,
Vol. 40,
Issue. 1,
p.
56.
Bojdecki, Tomasz
and
Gorostiza, Luis G.
1995.
Self-intersection local time for Gaussian G′(Rd)-processes: Existence, path continuity and examples.
Stochastic Processes and their Applications,
Vol. 60,
Issue. 2,
p.
191.
Talarczyk, Anna
2001.
Self-intersection local time of order k for Gaussian processes in S′(Rd).
Stochastic Processes and their Applications,
Vol. 96,
Issue. 1,
p.
17.

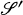 -valued Gaussian processes
-valued Gaussian processes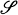 be the Schwartz space of all rapidly decreasing functions on
be the Schwartz space of all rapidly decreasing functions on 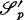 be the space of all elements of
be the space of all elements of 