Hostname: page-component-76c49bb84f-sz5hq Total loading time: 0 Render date: 2025-07-08T01:21:53.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Peterson-type dimension formulas for graded Lie superalgebras

Published online by Cambridge University Press:  22 January 2016

Seok-Jin Kang ,
Jae-Hoon Kwon  and
Young-Tak Oh
Seok-Jin Kang
Affiliation:
Korea Institute for Advanced Study, 207-43 Cheongryangri-dong, Dongdaemun-gu, Seoul 130-012, Korea, sjkang@kias.re.kr
Jae-Hoon Kwon
Affiliation:
Korea Institute for Advanced Study, 207-43 Cheongryangri-dong, Dongdaemun-gu, Seoul 130-012, Korea, jhkwon@math.snu.ac.kr
Young-Tak Oh
Affiliation:
Department of Mathematics, Seoul National University, Seoul 151-742, Korea, ohyt@math.snu.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 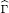be a free abelian group of finite rank, let Γ be a sub-semigroup of 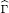satisfying certain finiteness conditions, and let 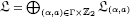be a (Γ × Z2)-graded Lie superalgebra. In this paper, by applying formal differential operators and the Laplacian to the denominator identity of 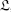, we derive a new recursive formula for the dimensions of homogeneous subspaces of 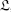. When applied to generalized Kac-Moody superalgebras, our formula yields a generalization of Peterson’s root multiplicity formula. We also obtain a Freudenthal-type weight multiplicity formula for highest weight modules over generalized Kac-Moody superalgebras.

Keywords

17A7017B0117B6517B7011F0311F22

Information

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 163 , September 2001 , pp. 107 - 144
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2000

References

[1] Borcherds, R. E., Generalized Kac-Moody algebras, J. Algebra, 115 (1988), 501–512.Google Scholar
[2] Borcherds, R. E., Monstrous moonshine and monstrous Lie super algebras, Invent. Math., 109 (1992), 405–444.Google Scholar
[3] Borcherds, R. E., Automorphic forms onOs+2,2(R) and infinite products, Invent. Math., 120 (1995), 161–213.Google Scholar
[4] Cartan, H. and Eilenberg, S., Homological algebra, Princeton Mathematics Series, Princeton University, 1956.Google Scholar
[5] Conway, J. H. and Norton, S., Monstrous moonshine, Bull. Lond. Math. Soc, 11 (1979), 308–339.Google Scholar
[6] Fuks, D. B., Cohomology of infinite dimensional Lie algebras, Consultant Bureau, New York, 1986.Google Scholar
[7] Im, Y.-J., Defining relations of generalized Kac-Moody superalgebras, M. S. thesis, Seoul National University (1998).Google Scholar
[8] Kac, V. G., Infinite-dimensional Lie algebras and Dedekind’s η-function, Funct. Anal. Appl., 8 (1974), 68–70.Google Scholar
[9] Kac, V. G., Lie superalgebras, Adv. in Math., 26 (1977), 8–96.Google Scholar
[10] Kac, V. G., Infinite dimensional algebras, Dedekind’s η-function, classical Möbius function and the very strange formula, Adv. in Math., 30 (1978), 85–136.Google Scholar
[11] Kac, V. G., Infinite Dimensional Lie Algebras, Cambridge Univ. Press, 3rd ed., 1990.Google Scholar
[12] Kang, S.-J., Generalized Kac-Moody algebras and the modular function j, Math. Ann., 298 (1994), 373–384.Google Scholar
[13] Kang, S.-J., Graded Lie superalgebras and the superdimension formula, J. Algebra, 204 (1998), 597–655.CrossRefGoogle Scholar
[14] Kang, S.-J. and Kim, M.-H., Dimension formula for graded Lie algebras and its applications, Trans. Amer. Math. Soc., 351 (1999), 4281–4336.Google Scholar
[15] Kang, S.-J. and Kwon, J.-H., Graded Lie superalgebras, supertrace formula, and orbit Lie superalgebra, Proc. London Math. Soc, 81 (1998), 675–724.Google Scholar
[16] Kang, S.-J. and Oh, Y.-T., Peterson-type supertrace formula for graded Lie superalgebras and super-replicable functions, in preparation.Google Scholar
[17] Koo, J.-K. and Oh, Y.-T, Freudenthal-type multiplicity formulas for generalized Kac-Moody superalgebras, Comm. Algebra, 29(1) (2001), 225–244.Google Scholar
[18] Liu, L.-S., Kostant’s formula for Kac-Moody Lie algebras, J. Algebra, 149 (1992), 155–178.CrossRefGoogle Scholar
[19] Macdonald, I. G., Affine root systems and Dedekind’s η-function, Invent. Math., 15 (1972), 91–143.Google Scholar
[20] Macdonald, I. G., Symmetric Functions and Hall Polynomials, Oxford Univ. Press, England, 2nd ed., 1995.Google Scholar
[21] Miyamoto, M., A generalization of Borcherds algebra and denominator formula, J. Algebra, 180 (1996), 631–651.Google Scholar
[22] Peterson, D. H., Freudenthal-type formulas for root and weight multiplicities, Preprint (1983), unpublished.Google Scholar
[23] Ray, U., A character formula for generalized Kac-Moody superalgebras, J. Algebra, 177 (1995), 154–163.Google Scholar