Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-24T04:24:06.773Z Has data issue: false hasContentIssue false
  • English
  • Français

PL DENSITY INVARIANT FOR TYPE II DEGENERATING K3 SURFACES, MODULI COMPACTIFICATION AND HYPER-KÄHLER METRIC

Part of: Global differential geometry Surfaces and higher-dimensional varieties Families, fibrations

Published online by Cambridge University Press:  03 November 2021

YUJI ODAKA Open the ORCID record for YUJI ODAKA [Opens in a new window]
YUJI ODAKA*
Affiliation:
Department of Mathematics Kyoto University Kyoto, Japan yodaka@math.kyoto-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

A protagonist here is a new-type invariant for type II degenerations of K3 surfaces, which is explicit piecewise linear convex function from the interval with at most 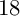$18$ nonlinear points. Forgetting its actual function behavior, it also classifies the type II degenerations into several combinatorial types, depending on the type of root lattices as appeared in classical examples.

From differential geometric viewpoint, the function is obtained as the density function of the limit measure on the collapsing hyper-Kähler metrics to conjectural segments, as in [HSZ19]. On the way, we also reconstruct a moduli compactification of elliptic K3 surfaces by [AB19], [ABE20], [Brun15] in a more elementary manner, and analyze the cusps more explicitly.

We also interpret the glued hyper-Kähler fibration of [HSVZ18] as a special case from our viewpoint, and discuss other cases, and possible relations with Landau–Ginzburg models in the mirror symmetry context.

MSC classification

Primary: 14J28: $K3$ surfaces and Enriques surfaces
Secondary: 14D20: Algebraic moduli problems, moduli of vector bundles 53C26: Hyper-Kähler and quaternionic Kähler geometry, “special” geometry
Type
Article
Information
Nagoya Mathematical Journal , Volume 247 , September 2022 , pp. 574 - 614
Check for updates
Copyright
© (2021) The Authors. The publishing rights in this article are licenced to Foundation Nagoya Mathematical Journal under an exclusive license

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is partially supported by KAKENHI 18K13389 (Grant-in-Aid for Early-Career Scientists), KAKENHI 16H06335 (Grant-in-Aid for Scientific Research (S)), and KAKENHI 20H00112 (Grant-in-Aid for Scientific Research (A)) during this research.

References

Abramovich, D. and Vistoli, A., Compactifying the space of stable maps , J. Amer. Math. Soc. 15 (2002), 27–75.CrossRefGoogle Scholar
Alexeev, V., Brunyate, A., and Engel, P., Compactifications of moduli of elliptic K3 surfaces: Stable pairs and toroidal, to appear in Geometry and Topology, arXiv:2002.07127v3 Google Scholar
Alexeev, V., Engel, P., and Thompson, A., Stable pair compactification of moduli of K3 surfaces of degree 2, preprint, arXiv:1903.09742 Google Scholar
Alexeev, V. and Nakamura, I., On Mumford’s construction of degenerating abelian varieties , Tohoku Math. J. 51 (1999), 399–420.CrossRefGoogle Scholar
Ambro, F., The moduli b-divisor of an lc-trivial fibration , Compos. Math. 141 (2005), 385–403.CrossRefGoogle Scholar
Arezzo, C. and Pacard, F., Blowing up and desingularizing Kähler orbifolds with constant scalar curvature , Acta Math. 196 (2006), 179–228.CrossRefGoogle Scholar
Artin, M. and Swinnerton-Dyer, H. P. F., The Shafarevich–Tate conjecture for pencils of elliptic curves on K3 surfaces , Invent. Math. 20 (1973), 249–266.CrossRefGoogle Scholar
Ascher, K. and Bejleri, D., Compact moduli spaces of elliptic K3 surfaces, preprint, arXiv:1902.10686v3 Google Scholar
Ash, A., Mumford, D., Rapoport, M., and Tai, Y.-S., Smooth Compactifications of Locally Symmetric Varieties, 2nd ed., Cambridge Math. Libr., Cambridge Univ. Press, Cambridge, 2010.CrossRefGoogle Scholar
Auroux, D., Katzarkov, L., and Orlov, D., Mirror symmetry for Del Pezzo surfaces: Vanishing cycles and coherent sheaves , Invent. Math. 166 (2006), 537–582.CrossRefGoogle Scholar
Bernstein, I. N. and Shvartsman, O. V., Chevalley’s theorem for complex crystallographic Coxeter groups (in Russian), Funct. Anal. Appl. 12 (1978), 308–310.Google Scholar
Boucksom, S. and Jonsson, M., Tropical and non-archimedean limits of degenerating families of volume forms , J. Éc. polytech. Math. 4 (2017), 87–139.CrossRefGoogle Scholar
Brunyate, A., A modular compactification of the space of elliptic K3 surfaces, Ph.D. dissertation, University of Georgia, 2015.Google Scholar
Bryan, J. and Leung, N. C., The enumerative geometry of K3 surfaces and modular forms , J. Amer. Math. Soc. 13 (2000), 371–410.CrossRefGoogle Scholar
Carl, M., Pumperla, M., and Siebert, B., A tropical view on Landau–Ginzburg models, preprint.Google Scholar
Cheeger, J., Fukaya, K., and Gromov, M., Nilpotent structures and invariant metrics on collapsed manifolds , J. Amer. Math. Soc. 5 (1992), 327–372.Google Scholar
Chen, G. and Chen, X.-X., Gravitational instantons with faster than quadratic curvature decay (III) , Math. Ann. 380 (2021), 687–717.CrossRefGoogle Scholar
Clingher, A. and Doran, C., Modular invariants for lattice polarized K3 surfaces , Michigan Math. J. 55 (2007), 355–393.CrossRefGoogle Scholar
Clingher, A. and Morgan, J., Mathematics underlying the F-theory/heterotic string duality in eight dimensions , Comm. Math. Phys. 254 (2005), 513–563.CrossRefGoogle Scholar
Collins, T., Jacob, A., and Lin, Y.-S., Special Lagrangian submanifolds of log Calabi–Yau manifolds , Duke Math. J. 170 (2021), 1291–1375.Google Scholar
Cox, D., The homogenous coordinate ring of a toric variety , J. Algebraic Geom. 4 (1995), 17–50.Google Scholar
Davenport, H., On f 3(t) − g 2(t), Norske Vid. Slesk. Forh. (Trondheim) 38 (1965), 86–87.Google Scholar
Dolgachev, I., Mirror symmetry for lattice polarised K3 surfaces , J. Math. Sci. 81 (1996), 2599–2630.CrossRefGoogle Scholar
Donaldson, S., Scalar curvature and stability of toric varieties , J. Differential. Geom. 62 (2002), 289–349.CrossRefGoogle Scholar
Doran, C. F., Harder, A., and Thompson, A., Mirror symmetry, Tyurin degenerations and fibrations on Calabi–Yau manifolds , Proc. Conf. String Math. 2015 (2017), 93–131.Google Scholar
Drézet, J.-M., “ Luna’s slice theorem and applications ” in Algebraic Group Actions and Quotients, Hindawi, Cairo, 2004, 39–89.Google Scholar
Eguchi, T., Hori, K., and Xiong, C.-S., Gravitational quantum cohomology , Internat. J. Modern Phys. A 12 (1997), 1743–1782.CrossRefGoogle Scholar
Engel, P. and Friedman, R., Smoothings and rational double point adjacencies for cusp singularities , J. Differential. Geom. 118(1): (2021), 23–100.Google Scholar
Friedman, R., On the geometry of anticanonical pairs, preprint, arXiv:1502.02560.Google Scholar
Friedman, R., A new proof of the global Torelli theorem for K3 surfaces , Ann. of Math. 120 (1984), 237–269.CrossRefGoogle Scholar
Friedman, R. and Morgan, J., Smooth Four-Manifolds and Complex Surfaces, Ergeb. Math. Grenzgeb. (3) 27. Springer, Berlin, 1994.CrossRefGoogle Scholar
Friedman, R., Morgan, J., and Witten, E., Vector bundles and F-theory , Comm. Math. Phys. 187 (1997), 679–743.CrossRefGoogle Scholar
Friedman, R. and Scattone, F., Type III degenerations of K3 surfaces , Invent. Math. 83 (1986), 1–39.CrossRefGoogle Scholar
Fujino, O., Semipositivity theorems for moduli problems , Ann. of Math. 187 (2018), 639–665.CrossRefGoogle Scholar
Fukaya, K., Collapsing of Riemannian manifolds and eigenvalues of Laplace operator , Invent. Math. 87 (1987), 517–547.CrossRefGoogle Scholar
Fukaya, K., Collapsing Riemannian manifolds to ones of lower dimensions , J. Differential. Geom. 25 (1987), 139–156.CrossRefGoogle Scholar
Fukaya, K., Collapsing Riemannian manifolds to ones of lower dimensions, II , J. Math. Soc. Japan 41 (1989), 333–356.CrossRefGoogle Scholar
Gross, M., Hacking, P., and Keel, S., Moduli of surfaces with an anti-canonical cycle , Comp. Math 151 (2015), 265–291.Google Scholar
Hein, H.-J., Gravitational instantons from rational elliptic surfaces , J. Amer. Math. Soc. 25 (2012), 355–393.CrossRefGoogle Scholar
Hein, H.-J., Sun, S., Viaclovsky, J., and Zhang, R., Nilpotent structures and collapsing Ricci-flat metrics on K3 surfaces, preprint, arXiv:1807.09367.Google Scholar
Honda, S., Sun, S., and Zhang, R., A note on the collapsing geometry of hyper-Kähler four manifolds , Sci. China Math. 62 (2019), 2195–2210.CrossRefGoogle Scholar
Iitaka, S., Algebraic Geometry – An Introduction to Birational Geometry of Algebraic Varieties, Grad. Texts in Math. 76, Springer, Berlin, 1982.Google Scholar
Kas, A., Weierstrass normal forms and invariants of elliptic surfaces , Trans. Amer. Math. Soc. 225 (1977), 259–266.CrossRefGoogle Scholar
Keel, S. and Mori, S., Quotients by groupoids , Ann. of Math. (2) 145 (1997), 193–213.CrossRefGoogle Scholar
Kobayashi, R., “Ricci-flat Kähler metrics on affine algebraic manifolds and degenerations of Kähler–Einstein K3 surfaces” in Kähler Metrics and Moduli Spaces (ed. Ochiai, T.), Adv. Stud. Pure Math. 18-II, Academic Press, Cambridge, 1990, 257–311.Google Scholar
Kodaira, K., On compact analytic surfaces: II , Ann. of Math. 77 (1963), 563–626.CrossRefGoogle Scholar
Kondo, S., Type II degeneration of K3 surfaces, Nagoya J. Math 99 (1985), 11–30.CrossRefGoogle Scholar
Kontsevich, M. and Soibelman, Y., “Affine structures and non-archimedean analytic spaces” in The Unity of Mathematics, Progr. Math. 244, Birkhäuser, 2006, 321–385.Google Scholar
Kovács, S. and Patakfalvi, Z., Projectivity of the moduli space of stable log-varieties and subadditivity of log-Kodaira dimension , J. Amer. Math. Soc. 30 (2017), 959–1021.CrossRefGoogle Scholar
Laumon, G. and Moret-Bailly, L., Champs Algebriques, Ergeb. Math. 39, Springer, Berlin, 2000.Google Scholar
Laza, R. and O’Grady, K., Birational geometry of the moduli space of quartic K3 surfaces , Compos. Math. 155 (2019), 1655–1710.CrossRefGoogle Scholar
Liu, S.-C., Lee, T.-J., and Lee, Y.-S., On the complex affine structures of SYZ fibration of Del Pezzo surfaces, preprint, arXiv:2005.04825.Google Scholar
Looijenga, E., Root systems and elliptic curves , Invent. Math. 38 (1976), 17–32.Google Scholar
Luna, D., Slices étales, sur les groupes algébriques , Bull. Soc. Math. France 33 (1973), 81–105.Google Scholar
Manin, Y., Cubic Forms: Algebra, Geometry, Arithmetic, Elsevier, Amsterdam, 1986.Google Scholar
Miranda, R., The moduli of Weierstrass fibrations over ℙ1 , Math. Ann. 255 (1981), 379–394.CrossRefGoogle Scholar
Mumford, D., An analytic construction of degenerating abelian varieties over complete local rings , Compos. Math. 24 (1972), 239–272.Google Scholar
Mumford, D., Hirzebruch’s proportionality theorem in the noncompact case , Invent. Math. 42 (1977), 239–272.CrossRefGoogle Scholar
Odaka, Y., Polystable log Calabi–Yau varieties and gravitational instantons, preprint, arXiv:2009.13876.Google Scholar
Odaka, Y., Degenerated Calabi–Yau varieties with infinite components, moduli compactifications, and limit toroidal structures, preprint, arXiv:2011.12748.Google Scholar
Odaka, Y., Tropical geometric compactification of moduli, II: Ag case and holomorphic limits , Int. Math. Res. Not. IMRN 2019 (2018), no. 21, 6614–6660.CrossRefGoogle Scholar
Odaka, Y., On the K-stability and the moduli problem of varieties (in Japanese), Suugaku 72 2020 337–364.Google Scholar
Odaka, Y. and Oshima, Y., Collapsing K3 surfaces and moduli compactification , Proc. Japan Acad. Ser. A Math. Sci. 94 (2018), 81–86.CrossRefGoogle Scholar
Odaka, Y. and Oshima, Y., Collapsing K3 Surfaces, Tropical Geometry and Moduli Compactifications of Satake, Morgan–Shalen Type, MSJ Mem. 40, Math. Soc. Japan, Japan, 2021.CrossRefGoogle Scholar
Ohno, K., Minimizing CM degree and slope stability of projective varieties , Math. Proc. Cambridge Philos. Soc. (2021), 1–13.Google Scholar
Oshima, Y., Collapsing Ricci-flat metrics for type II degeneration of K3 surfaces, in preparation.Google Scholar
Park, J.-Y. and Schmitt, J., Arithmetic geometry of the moduli stack of Weierstrass fibrations over ℙ1, preprint, arXiv:2107.12231.Google Scholar
Pinkham, H. C., “Simple elliptic singularities, Del Pezzo surfaces and Cremona transformations” in Several Complex Variables, Proc. Sympos. Pure Math. XXX, Part 1, Williams Coll., 1975, Amer. Math. Soc., Providence, RI, 1977, 69–71.CrossRefGoogle Scholar
Satake, I., On representations and compactifications of symmetric Riemannian spaces , Ann. of Math. (2) 71 (1960), 77–110.Google Scholar
Satake, I., On compactifications of the quotient spaces for arithmetically defined discontinuous groups , Ann. of Math. (2) 72 (1960), 555–580.CrossRefGoogle Scholar
Seidel, P., “More about vanishing cycles and mutation, symplectic geometry and mirror symmetry” in Proceedings of the 4th KIAS Annual International Conference (Seoul, 2000) (eds. Fukaya, K., Oh, Y.-G., Ono, K., and Tian, G.), World Sci., Singapore, 2001, 429–465.Google Scholar
Shah, J., A complete moduli space for K3 surfaces of degree 2 , Ann. Math. 112 (1980), 485–510.CrossRefGoogle Scholar
Shepherd-Barron, N. I., “Degenerations with numerically effective canonical divisor” in R. Friedman and D. Morrison (eds.), The Birational Geometry of Degenerations (Cambridge, MA, 1981), Progr. Math. 29, Birkhäuser, Boston, 1983, 33–84.Google Scholar
Shioda, T., Elliptic surfaces and Davenport–Stothers triples , Comment. Math. Univ. St. Pauli 54 (2005), 49–68.Google Scholar
Silverman, J. H., The Arithmetic of Elliptic Curves, Grad. Texts in Math. 106, Springer, Berlin, 1985.Google Scholar
Stothers, W. W., Polynomial identities and hauptmoduln , Q. J. Math. 32 (1981), 349–370.CrossRefGoogle Scholar
Takeuchi, K., Some birational maps of Fano 3-folds , Compos. Math. 71 (1989), 265–283.Google Scholar
Tian, G. and Yau, S.-T., Complete Kähler manifolds with zero Ricci curvature I , J. Amer. Math. Sci. 3 (1990), 579–610.Google Scholar
Yau, S. T. and Zaslow, E., BPS states, string duality, and nodal curves on K3 , Nuclear Phys. B 471 (1996), 503–512.CrossRefGoogle Scholar
Zannier, U., On Davenport’s bound for the degree of f3 − g2 and Riemann’s existence theorem , Acta Arith. 71 (1995), 107–137.CrossRefGoogle Scholar