No CrossRef data available.
Published online by Cambridge University Press: 14 June 2019
Let 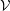 ${\mathcal{V}}$ be a complete discrete valuation ring of unequal characteristic with perfect residue field,
${\mathcal{V}}$ be a complete discrete valuation ring of unequal characteristic with perfect residue field, 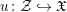 $u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ be a closed immersion of smooth, quasi-compact, separated formal schemes over
$u:{\mathcal{Z}}{\hookrightarrow}\mathfrak{X}$ be a closed immersion of smooth, quasi-compact, separated formal schemes over 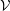 ${\mathcal{V}}$,
${\mathcal{V}}$,  $T$ be a divisor of
$T$ be a divisor of 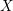 $X$ such that
$X$ such that 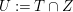 $U:=T\cap Z$ is a divisor of
$U:=T\cap Z$ is a divisor of 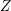 $Z$, and
$Z$, and 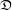 $\mathfrak{D}$ a strict normal crossing divisor of
$\mathfrak{D}$ a strict normal crossing divisor of 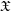 $\mathfrak{X}$ such that
$\mathfrak{X}$ such that 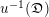 $u^{-1}(\mathfrak{D})$ is a strict normal crossing divisor of
$u^{-1}(\mathfrak{D})$ is a strict normal crossing divisor of 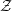 ${\mathcal{Z}}$. We pose
${\mathcal{Z}}$. We pose 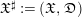 $\mathfrak{X}^{\sharp }:=(\mathfrak{X},\mathfrak{D})$,
$\mathfrak{X}^{\sharp }:=(\mathfrak{X},\mathfrak{D})$, 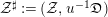 ${\mathcal{Z}}^{\sharp }:=({\mathcal{Z}},u^{-1}\mathfrak{D})$ and
${\mathcal{Z}}^{\sharp }:=({\mathcal{Z}},u^{-1}\mathfrak{D})$ and 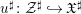 $u^{\sharp }:{\mathcal{Z}}^{\sharp }{\hookrightarrow}\mathfrak{X}^{\sharp }$ the exact closed immersion of smooth logarithmic formal schemes over
$u^{\sharp }:{\mathcal{Z}}^{\sharp }{\hookrightarrow}\mathfrak{X}^{\sharp }$ the exact closed immersion of smooth logarithmic formal schemes over 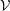 ${\mathcal{V}}$. In Berthelot’s theory of arithmetic
${\mathcal{V}}$. In Berthelot’s theory of arithmetic 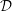 ${\mathcal{D}}$-modules, we work with the inductive system of sheaves of rings
${\mathcal{D}}$-modules, we work with the inductive system of sheaves of rings 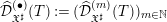 $\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T):=(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}(T))_{m\in \mathbb{N}}$, where
$\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T):=(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}(T))_{m\in \mathbb{N}}$, where 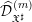 $\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}$ is the
$\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}$ is the 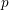 $p$-adic completion of the ring of differential operators of level
$p$-adic completion of the ring of differential operators of level  $m$ over
$m$ over 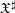 $\mathfrak{X}^{\sharp }$ and where
$\mathfrak{X}^{\sharp }$ and where 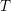 $T$ means that we add overconvergent singularities along the divisor
$T$ means that we add overconvergent singularities along the divisor 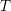 $T$. Moreover, Berthelot introduced the sheaf
$T$. Moreover, Berthelot introduced the sheaf 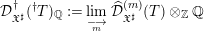 ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}:=\underset{\underset{m}{\longrightarrow }}{\lim }\,\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}(T)\otimes _{\mathbb{Z}}\mathbb{Q}$ of differential operators over
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}:=\underset{\underset{m}{\longrightarrow }}{\lim }\,\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(m)}(T)\otimes _{\mathbb{Z}}\mathbb{Q}$ of differential operators over 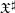 $\mathfrak{X}^{\sharp }$ of finite level with overconvergent singularities along
$\mathfrak{X}^{\sharp }$ of finite level with overconvergent singularities along 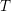 $T$. Let
$T$. Let 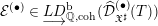 ${\mathcal{E}}^{(\bullet )}\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$ and
${\mathcal{E}}^{(\bullet )}\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{\mathfrak{X}^{\sharp }}^{(\bullet )}(T))$ and 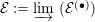 ${\mathcal{E}}:=\varinjlim ~({\mathcal{E}}^{(\bullet )})$ be the corresponding object of
${\mathcal{E}}:=\varinjlim ~({\mathcal{E}}^{(\bullet )})$ be the corresponding object of 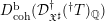 $D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$. In this paper, we study sufficient conditions on
$D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}})$. In this paper, we study sufficient conditions on 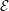 ${\mathcal{E}}$ so that if
${\mathcal{E}}$ so that if 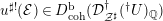 $u^{\sharp !}({\mathcal{E}})\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}})$ then
$u^{\sharp !}({\mathcal{E}})\in D_{\text{coh}}^{\text{b}}({\mathcal{D}}_{{\mathcal{Z}}^{\sharp }}^{\dagger }(\text{}^{\dagger }U)_{\mathbb{Q}})$ then 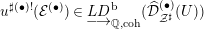 $u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )}(U))$. For instance, we check that this is the case when
$u^{\sharp (\bullet )!}({\mathcal{E}}^{(\bullet )})\in \underset{\displaystyle \longrightarrow }{LD}\text{}_{\mathbb{Q},\text{coh}}^{\text{b}}(\widehat{{\mathcal{D}}}_{{\mathcal{Z}}^{\sharp }}^{(\bullet )}(U))$. For instance, we check that this is the case when 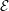 ${\mathcal{E}}$ is a coherent
${\mathcal{E}}$ is a coherent 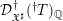 ${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module such that the cohomological spaces of
${\mathcal{D}}_{\mathfrak{X}^{\sharp }}^{\dagger }(\text{}^{\dagger }T)_{\mathbb{Q}}$-module such that the cohomological spaces of 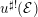 $u^{\sharp !}({\mathcal{E}})$ are isocrystals on
$u^{\sharp !}({\mathcal{E}})$ are isocrystals on 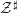 ${\mathcal{Z}}^{\sharp }$ overconvergent along
${\mathcal{Z}}^{\sharp }$ overconvergent along 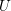 $U$.
$U$.