Article contents
Tensor Product Structure of Affine Demazure Modules and Limit Constructions
Published online by Cambridge University Press: 11 January 2016
Abstract
Let g be a simple complex Lie algebra, we denote by ĝ the affine Kac-Moody algebra associated to the extended Dynkin diagram of g. Let Λ0 be the fundamental weight of ĝ corresponding to the additional node of the extended Dynkin diagram. For a dominant integral g-coweight λ∨, the Demazure submodule V_λ∨ (mΛ0) is a g-module. We provide a description of the g-module structure as a tensor product of “smaller” Demazure modules. More precisely, for any partition of λ∨ = λ∑j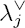 as a sum of dominant integral g-coweights, the Demazure module is (as g-module) isomorphic to ⊗jV_
as a sum of dominant integral g-coweights, the Demazure module is (as g-module) isomorphic to ⊗jV_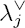 (mΛ0). For the “smallest” case, λ∨ = ω∨ a fundamental coweight, we provide for g of classical type a decomposition of V_ω∨(mΛ0) into irreducible g-modules, so this can be viewed as a natural generalization of the decomposition formulas in [13] and [16]. A comparison with the Uq (g)-characters of certain finite dimensional
(mΛ0). For the “smallest” case, λ∨ = ω∨ a fundamental coweight, we provide for g of classical type a decomposition of V_ω∨(mΛ0) into irreducible g-modules, so this can be viewed as a natural generalization of the decomposition formulas in [13] and [16]. A comparison with the Uq (g)-characters of certain finite dimensional 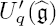 -modules (Kirillov-Reshetikhin-modules) suggests furthermore that all quantized Demazure modules V_λ∨,q(mΛ0) can be naturally endowed with the structure of a
-modules (Kirillov-Reshetikhin-modules) suggests furthermore that all quantized Demazure modules V_λ∨,q(mΛ0) can be naturally endowed with the structure of a 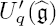 -module. We prove, in the classical case (and for a lot of non-classical cases), a conjecture by Kashiwara [10], that the “smallest” Demazure modules are, when viewed as g-modules, isomorphic to some KR-modules. For an integral dominant ĝ-weight Λ let V(Λ) be the corresponding irreducible ĝ-representation. Using the tensor product decomposition for Demazure modules, we give a description of the g-module structure of V(Λ) as a semi-infinite tensor product of finite dimensional g-modules. The case of twisted affine Kac-Moody algebras can be treated in the same way, some details are worked out in the last section.
-module. We prove, in the classical case (and for a lot of non-classical cases), a conjecture by Kashiwara [10], that the “smallest” Demazure modules are, when viewed as g-modules, isomorphic to some KR-modules. For an integral dominant ĝ-weight Λ let V(Λ) be the corresponding irreducible ĝ-representation. Using the tensor product decomposition for Demazure modules, we give a description of the g-module structure of V(Λ) as a semi-infinite tensor product of finite dimensional g-modules. The case of twisted affine Kac-Moody algebras can be treated in the same way, some details are worked out in the last section.
Information
- Type
- Research Article
- Information
- Nagoya Mathematical Journal , Volume 182: Special Issue Celebrating the 60th Birthday of George Lusztig , June 2006 , pp. 171 - 198
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 2006
References
- 42
- Cited by

