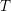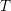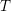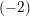Introduction
Tilting objects give rise to equivalences between derived categories but when restricted to the underlying abelian categories, they almost never induce equivalences. In this article, we are interested in equivalences of abelian categories. Therefore, we need to consider partial tilting objects. The aim of this paper is to find conditions when a partial tilting object induces an equivalence of abelian categories. This will be applied to surfaces with chains of negative curves. Before we start with our geometric application, we consider the problem abstractly.
Let
![]() $T$
be a partial tilting object in a
$T$
be a partial tilting object in a
![]() $\mathbf{k}$
-linear abelian category
$\mathbf{k}$
-linear abelian category
![]() ${\mathcal{A}}$
. Then there is a well-established equivalence of triangulated categories
${\mathcal{A}}$
. Then there is a well-established equivalence of triangulated categories
![]() $\operatorname{RHom}(T,-):\langle T\rangle \stackrel{{\sim}}{\longrightarrow }{\mathcal{D}}^{b}(\text{mod}\text{-}\unicode[STIX]{x1D6EC})$
, where we write
$\operatorname{RHom}(T,-):\langle T\rangle \stackrel{{\sim}}{\longrightarrow }{\mathcal{D}}^{b}(\text{mod}\text{-}\unicode[STIX]{x1D6EC})$
, where we write
![]() $\unicode[STIX]{x1D6EC}=\operatorname{End}(T)$
for the endomorphism algebra and
$\unicode[STIX]{x1D6EC}=\operatorname{End}(T)$
for the endomorphism algebra and
![]() $\langle T\rangle$
for the triangulated category generated by
$\langle T\rangle$
for the triangulated category generated by
![]() $T$
which is closed under summands. We say that
$T$
which is closed under summands. We say that
![]() $T$
is exact partial tilting if all surjective morphisms in
$T$
is exact partial tilting if all surjective morphisms in
![]() $\operatorname{add}(T)$
split, see Definition 1.1.
$\operatorname{add}(T)$
split, see Definition 1.1.
Theorem A. Let
![]() $T$
be an exact partial tilting object of
$T$
be an exact partial tilting object of
![]() ${\mathcal{A}}$
. Then there is an equivalence of abelian categories
${\mathcal{A}}$
. Then there is an equivalence of abelian categories
![]() $\operatorname{Hom}(T,-):\langle T\rangle \cap {\mathcal{A}}\stackrel{{\sim}}{\longrightarrow }\text{mod}\text{-}\unicode[STIX]{x1D6EC}$
.
$\operatorname{Hom}(T,-):\langle T\rangle \cap {\mathcal{A}}\stackrel{{\sim}}{\longrightarrow }\text{mod}\text{-}\unicode[STIX]{x1D6EC}$
.
Moreover,
![]() $\langle T\rangle \cap {\mathcal{A}}$
coincides with the full subcategory of
$\langle T\rangle \cap {\mathcal{A}}$
coincides with the full subcategory of
![]() ${\mathcal{A}}$
consisting of objects admitting a left resolution by objects of
${\mathcal{A}}$
consisting of objects admitting a left resolution by objects of
![]() $\operatorname{add}(T)$
.
$\operatorname{add}(T)$
.
See Proposition 1.3 for the proof. In Proposition 1.6, we show how exact partial tilting objects arise as universal extensions of exceptional sequences of objects from
![]() ${\mathcal{A}}$
with special properties. (See Section 1.2 for universal extensions of exceptional sequences with vanishing
${\mathcal{A}}$
with special properties. (See Section 1.2 for universal extensions of exceptional sequences with vanishing
![]() $\operatorname{Ext}^{{>}1}$
.)
$\operatorname{Ext}^{{>}1}$
.)
Later we are mainly interested in geometric applications. In fact, for any rational surface there always exists a tilting object [Reference Hille and Perling7]. Starting with a chain of curves, we consider an exceptional sequence adapted to this chain. One expects to understand sheaves in a certain neighborhood using the corresponding exact tilting objects. For further results on existence and further properties of exceptional sequences on rational surfaces, we refer to [Reference Hille and Perling6]. For exceptional sequences that are not strong, the algebras can be chosen to be quasi-hereditary. Essentially, this means that the category of filtered modules (with respect to the exceptional sequence) is well understood. We use this property at several places, however, never need the theory of quasi-hereditary algebras in more detail.
Our main exact partial tilting example concerns chains of rational curves of negative self-intersection (short: negative curves) on rational surfaces. More precisely, we study the abelian and triangulated categories generated by ideal sheaves of a chain of negative curves which form a special exceptional sequence. The universal extension of this sequence is an exact tilting bundle. For a more precise statement, see Theorem 2.5.
Theorem B. Let
![]() $X$
be a smooth, projective surface such that
$X$
be a smooth, projective surface such that
![]() ${\mathcal{O}}_{X}$
is exceptional, and let
${\mathcal{O}}_{X}$
is exceptional, and let
![]() $C_{1},C_{2},\ldots ,C_{t}$
be an
$C_{1},C_{2},\ldots ,C_{t}$
be an
![]() $A_{t}$
-chain of smooth, rational curves with all
$A_{t}$
-chain of smooth, rational curves with all
![]() $C_{i}^{2}\leqslant -2$
. Then
$C_{i}^{2}\leqslant -2$
. Then
![]() ${\mathcal{E}}:=({\mathcal{O}}(-C_{1}-\cdots -C_{t}),\ldots ,{\mathcal{O}}(-C_{1}),{\mathcal{O}})$
is an exceptional sequence such that its universal extension
${\mathcal{E}}:=({\mathcal{O}}(-C_{1}-\cdots -C_{t}),\ldots ,{\mathcal{O}}(-C_{1}),{\mathcal{O}})$
is an exceptional sequence such that its universal extension
![]() $T$
is an exact partial tilting bundle, that is the associated equivalence of triangulated categories restricts to an equivalence of abelian categories:
$T$
is an exact partial tilting bundle, that is the associated equivalence of triangulated categories restricts to an equivalence of abelian categories:

Above,
![]() ${\mathcal{E}}\subset {\mathcal{D}}^{b}(X)$
also denotes the triangulated category generated by the exceptional sequence. This result is one technical tool used in [Reference Kalck and Karmazyn10] for a Knörrer-type equivalence of singularity categories.
${\mathcal{E}}\subset {\mathcal{D}}^{b}(X)$
also denotes the triangulated category generated by the exceptional sequence. This result is one technical tool used in [Reference Kalck and Karmazyn10] for a Knörrer-type equivalence of singularity categories.
For an exact partial tilting sheaf, the connection between geometry and representation theory provided by tilting is even stronger than usual. On the negative side, such a strong connection can never work for the category of coherent sheaves itself, since it does not contain projective objects and any equivalence between abelian categories preserves projective objects. Thus we are forced to consider partial tilting sheaves to get an equivalence between abelian categories. On the other hand, this equivalence provides us with projective objects in
![]() $\text{Coh}_{{\mathcal{E}}}(X)$
. Thus, we essentially need to construct sufficiently many projective objects (a projective generator) to get the result.
$\text{Coh}_{{\mathcal{E}}}(X)$
. Thus, we essentially need to construct sufficiently many projective objects (a projective generator) to get the result.
To illustrate the theorem in a small example, we consider just one smooth, rational curve
![]() $C$
on a rational surface
$C$
on a rational surface
![]() $X$
. Put
$X$
. Put
![]() $r:=-(C^{2}+1)$
. For
$r:=-(C^{2}+1)$
. For
![]() $r\leqslant 0$
, that is
$r\leqslant 0$
, that is
![]() $C^{2}\geqslant -1$
, the bundle
$C^{2}\geqslant -1$
, the bundle
![]() ${\mathcal{O}}\oplus {\mathcal{O}}(-C)$
is a tilting bundle; it is exact only for
${\mathcal{O}}\oplus {\mathcal{O}}(-C)$
is a tilting bundle; it is exact only for
![]() $C^{2}=-1$
. On the other hand, if
$C^{2}=-1$
. On the other hand, if
![]() $r\geqslant 1$
, that is
$r\geqslant 1$
, that is
![]() $C^{2}\leqslant -2$
, then
$C^{2}\leqslant -2$
, then
![]() $r=\dim \operatorname{Ext}^{1}({\mathcal{O}}(-C),{\mathcal{O}})$
and we can consider the universal extension of
$r=\dim \operatorname{Ext}^{1}({\mathcal{O}}(-C),{\mathcal{O}})$
and we can consider the universal extension of
![]() ${\mathcal{O}}(-C)$
by
${\mathcal{O}}(-C)$
by
![]() ${\mathcal{O}}$
; it is
${\mathcal{O}}$
; it is
![]() $0\rightarrow {\mathcal{O}}^{r}\rightarrow \binom{{\mathcal{O}}(-C)}{{\mathcal{O}}^{r}}\rightarrow {\mathcal{O}}(-C)\rightarrow 0$
. Then the exceptional sequence
$0\rightarrow {\mathcal{O}}^{r}\rightarrow \binom{{\mathcal{O}}(-C)}{{\mathcal{O}}^{r}}\rightarrow {\mathcal{O}}(-C)\rightarrow 0$
. Then the exceptional sequence
![]() $({\mathcal{O}}(-C),{\mathcal{O}})$
has an exact partial tilting bundle: the direct sum
$({\mathcal{O}}(-C),{\mathcal{O}})$
has an exact partial tilting bundle: the direct sum
![]() ${\mathcal{O}}\oplus \binom{{\mathcal{O}}(-C)}{{\mathcal{O}}^{r}}$
. For details, see Example 2.4.
${\mathcal{O}}\oplus \binom{{\mathcal{O}}(-C)}{{\mathcal{O}}^{r}}$
. For details, see Example 2.4.
The case of a chain of
![]() $(-2)$
-curves is of particular interest, since there exist many spherical objects in the subcategory
$(-2)$
-curves is of particular interest, since there exist many spherical objects in the subcategory
![]() $\text{Coh}_{{\mathcal{E}}}(X)$
. Those spherical objects induce a braid group action by equivalences of the derived category. In this particular case, the algebra
$\text{Coh}_{{\mathcal{E}}}(X)$
. Those spherical objects induce a braid group action by equivalences of the derived category. In this particular case, the algebra
![]() $\unicode[STIX]{x1D6EC}$
of Theorem B is well-known in representation theory: it is the Auslander algebra of
$\unicode[STIX]{x1D6EC}$
of Theorem B is well-known in representation theory: it is the Auslander algebra of
![]() $\mathbf{k}[T]/T^{t+1}$
. The finite-dimensional algebra
$\mathbf{k}[T]/T^{t+1}$
. The finite-dimensional algebra
![]() $\unicode[STIX]{x1D6EC}$
has previously been studied by several authors, see [Reference Brüstle, Hille, Ringel and Röhrle4] for references.
$\unicode[STIX]{x1D6EC}$
has previously been studied by several authors, see [Reference Brüstle, Hille, Ringel and Röhrle4] for references.
Here, we study—from the geometric point of view—categories encompassing modules over the Auslander algebra of
![]() $\mathbf{k}[T]/T^{t+1}$
.
$\mathbf{k}[T]/T^{t+1}$
.
1 Exact tilting and adapted exceptional sequences
All varieties, algebras and categories are over a ground field
![]() $\mathbf{k}$
which is assumed to be algebraically closed.
$\mathbf{k}$
which is assumed to be algebraically closed.
1.1 Exact partial tilting objects
Let
![]() ${\mathcal{A}}$
be an abelian category, and
${\mathcal{A}}$
be an abelian category, and
![]() $T\in {\mathcal{A}}$
be a partial tilting object, that is
$T\in {\mathcal{A}}$
be a partial tilting object, that is
![]() $\operatorname{Ext}^{{>}0}(T,T)=0$
with endomorphism algebra
$\operatorname{Ext}^{{>}0}(T,T)=0$
with endomorphism algebra
![]() $\unicode[STIX]{x1D6EC}:=\operatorname{End}(T)$
. We write
$\unicode[STIX]{x1D6EC}:=\operatorname{End}(T)$
. We write
![]() $\langle T\rangle$
for the triangulated category generated by
$\langle T\rangle$
for the triangulated category generated by
![]() $T$
(closed under summands) inside
$T$
(closed under summands) inside
![]() ${\mathcal{D}}^{b}({\mathcal{A}})$
. The category
${\mathcal{D}}^{b}({\mathcal{A}})$
. The category
![]() $\langle T\rangle \cap {\mathcal{A}}$
is, in general, additive but not abelian.
$\langle T\rangle \cap {\mathcal{A}}$
is, in general, additive but not abelian.
Classical tilting theory gives an equivalence of triangulated categories
![]() $\operatorname{RHom}(T,-):\langle T\rangle \stackrel{{\sim}}{\longrightarrow }{\mathcal{D}}^{b}(\text{mod}\text{-}\unicode[STIX]{x1D6EC})$
. We introduce the following special property which, roughly saying, states that there are no nontrivial surjections in
$\operatorname{RHom}(T,-):\langle T\rangle \stackrel{{\sim}}{\longrightarrow }{\mathcal{D}}^{b}(\text{mod}\text{-}\unicode[STIX]{x1D6EC})$
. We introduce the following special property which, roughly saying, states that there are no nontrivial surjections in
![]() $T$
.
$T$
.
Definition 1.1. A partial tilting object
![]() $T\in {\mathcal{A}}$
is called exact partial tilting if every surjection between objects in
$T\in {\mathcal{A}}$
is called exact partial tilting if every surjection between objects in
![]() $\operatorname{add}(T)$
splits.
$\operatorname{add}(T)$
splits.
Recall that
![]() $\operatorname{add}(T)$
is the additive category generated by
$\operatorname{add}(T)$
is the additive category generated by
![]() $T$
, that is the subcategory of
$T$
, that is the subcategory of
![]() ${\mathcal{A}}$
consisting of finite direct sums of summands of
${\mathcal{A}}$
consisting of finite direct sums of summands of
![]() $T$
. For a concrete exact tilting object from geometry, see Section 2.
$T$
. For a concrete exact tilting object from geometry, see Section 2.
Lemma 1.2. A partial tilting object
![]() $T$
is exact partial tilting if and only if
$T$
is exact partial tilting if and only if
![]() $S{\twoheadrightarrow}S^{\prime }$
implies
$S{\twoheadrightarrow}S^{\prime }$
implies
![]() $\operatorname{Hom}(T_{i},S){\twoheadrightarrow}\operatorname{Hom}(T_{i},S^{\prime })$
for any indecomposable summand
$\operatorname{Hom}(T_{i},S){\twoheadrightarrow}\operatorname{Hom}(T_{i},S^{\prime })$
for any indecomposable summand
![]() $T_{i}$
of
$T_{i}$
of
![]() $T$
and
$T$
and
![]() $S,S^{\prime }\in \operatorname{add}(T)$
.
$S,S^{\prime }\in \operatorname{add}(T)$
.
Proof. If
![]() $T$
is exact partial tilting, then the surjection
$T$
is exact partial tilting, then the surjection
![]() $S{\twoheadrightarrow}S^{\prime }$
admits a section
$S{\twoheadrightarrow}S^{\prime }$
admits a section
![]() $\unicode[STIX]{x1D70E}:S^{\prime }\rightarrow S$
. Hence any morphism
$\unicode[STIX]{x1D70E}:S^{\prime }\rightarrow S$
. Hence any morphism
![]() $f:T_{i}\rightarrow S^{\prime }$
is induced by
$f:T_{i}\rightarrow S^{\prime }$
is induced by
![]() $\unicode[STIX]{x1D70E}f$
.
$\unicode[STIX]{x1D70E}f$
.
On the other hand, assume that
![]() $T$
satisfies the property of the lemma, and let
$T$
satisfies the property of the lemma, and let
![]() $S{\twoheadrightarrow}S^{\prime }$
be a surjection of sums of summands of
$S{\twoheadrightarrow}S^{\prime }$
be a surjection of sums of summands of
![]() $T$
. If
$T$
. If
![]() $S^{\prime }$
is indecomposable, then taking
$S^{\prime }$
is indecomposable, then taking
![]() $T_{i}=S^{\prime }$
in that property gives the desired splitting right away. If
$T_{i}=S^{\prime }$
in that property gives the desired splitting right away. If
![]() $S^{\prime }$
is decomposable, then the induced surjections onto direct summands of
$S^{\prime }$
is decomposable, then the induced surjections onto direct summands of
![]() $S^{\prime }$
, that is
$S^{\prime }$
, that is
![]() $S{\twoheadrightarrow}S^{\prime }{\twoheadrightarrow}S_{i}^{\prime }$
, split and can be combined to a section
$S{\twoheadrightarrow}S^{\prime }{\twoheadrightarrow}S_{i}^{\prime }$
, split and can be combined to a section
![]() $S^{\prime }\rightarrow S$
.◻
$S^{\prime }\rightarrow S$
.◻
Proposition 1.3. Let
![]() $T\in {\mathcal{A}}$
be an exact partial tilting object and
$T\in {\mathcal{A}}$
be an exact partial tilting object and
![]() $\unicode[STIX]{x1D6EC}=\operatorname{End}(T)$
. Then the equivalence
$\unicode[STIX]{x1D6EC}=\operatorname{End}(T)$
. Then the equivalence
![]() $\unicode[STIX]{x1D6F7}=\operatorname{RHom}(T,-):\langle T\rangle \stackrel{{\sim}}{\longrightarrow }{\mathcal{D}}^{b}(\text{mod}\text{-}\unicode[STIX]{x1D6EC})$
restricts to an equivalence of abelian categories
$\unicode[STIX]{x1D6F7}=\operatorname{RHom}(T,-):\langle T\rangle \stackrel{{\sim}}{\longrightarrow }{\mathcal{D}}^{b}(\text{mod}\text{-}\unicode[STIX]{x1D6EC})$
restricts to an equivalence of abelian categories
![]() $\langle T\rangle \cap {\mathcal{A}}\stackrel{{\sim}}{\longrightarrow }\text{mod}\text{-}\unicode[STIX]{x1D6EC}$
.
$\langle T\rangle \cap {\mathcal{A}}\stackrel{{\sim}}{\longrightarrow }\text{mod}\text{-}\unicode[STIX]{x1D6EC}$
.
Proof. The functor
![]() $\unicode[STIX]{x1D6F7}$
induces an equivalence between the abelian categories
$\unicode[STIX]{x1D6F7}$
induces an equivalence between the abelian categories
![]() $\text{mod}\text{-}\unicode[STIX]{x1D6EC}$
and
$\text{mod}\text{-}\unicode[STIX]{x1D6EC}$
and
![]() $\unicode[STIX]{x1D6F7}^{-1}(\text{mod}\text{-}\unicode[STIX]{x1D6EC})$
. Let
$\unicode[STIX]{x1D6F7}^{-1}(\text{mod}\text{-}\unicode[STIX]{x1D6EC})$
. Let
![]() $F\in \langle T\rangle \cap {\mathcal{A}}$
. We want to show that
$F\in \langle T\rangle \cap {\mathcal{A}}$
. We want to show that
![]() $\unicode[STIX]{x1D6F7}(F)\in \text{mod}\text{-}\unicode[STIX]{x1D6EC}$
. As
$\unicode[STIX]{x1D6F7}(F)\in \text{mod}\text{-}\unicode[STIX]{x1D6EC}$
. As
![]() $F\in \langle T\rangle$
and
$F\in \langle T\rangle$
and
![]() $\operatorname{Hom}^{i}(T,T)=0$
for all
$\operatorname{Hom}^{i}(T,T)=0$
for all
![]() $i\neq 0$
(
$i\neq 0$
(
![]() $T$
partial tilting), there is an isomorphism
$T$
partial tilting), there is an isomorphism
![]() $F\cong D^{\bullet }$
, where each component
$F\cong D^{\bullet }$
, where each component
![]() $D^{i}$
consists of summands from
$D^{i}$
consists of summands from
![]() $T$
.
$T$
.
By assumption,
![]() $D^{\bullet }$
has a single cohomology object
$D^{\bullet }$
has a single cohomology object
![]() $F$
in degree 0. We now show that
$F$
in degree 0. We now show that
![]() $D^{\bullet }$
can be truncated at 0; thus without loss of generality
$D^{\bullet }$
can be truncated at 0; thus without loss of generality
![]() $D^{\bullet }$
is a
$D^{\bullet }$
is a
![]() $T$
-resolution of
$T$
-resolution of
![]() $F$
. If
$F$
. If
![]() $D^{\bullet }=[\cdots \rightarrow D^{0}\rightarrow D^{1}\rightarrow \cdots D^{a}]$
has components in positive degree, then we look at the two rightmost nonzero terms: these form a surjection
$D^{\bullet }=[\cdots \rightarrow D^{0}\rightarrow D^{1}\rightarrow \cdots D^{a}]$
has components in positive degree, then we look at the two rightmost nonzero terms: these form a surjection
![]() $s:D^{a-1}{\twoheadrightarrow}D^{a}$
and because
$s:D^{a-1}{\twoheadrightarrow}D^{a}$
and because
![]() $T$
is exact partial tilting, the induced map
$T$
is exact partial tilting, the induced map
![]() $\operatorname{Hom}(D^{a},D^{a-1})\rightarrow \operatorname{Hom}(D^{a},D^{a})$
is also surjective. Hence we find a section of
$\operatorname{Hom}(D^{a},D^{a-1})\rightarrow \operatorname{Hom}(D^{a},D^{a})$
is also surjective. Hence we find a section of
![]() $s$
and can split off the subcomplex
$s$
and can split off the subcomplex
![]() $D^{a}\rightarrow D^{a}$
as a direct summand of
$D^{a}\rightarrow D^{a}$
as a direct summand of
![]() $D^{\bullet }$
. Iterating this process leaves us with a complex ending in degree 0, hence a resolution of
$D^{\bullet }$
. Iterating this process leaves us with a complex ending in degree 0, hence a resolution of
![]() $F$
.
$F$
.
Recall that
![]() $\unicode[STIX]{x1D6F7}(T_{i})=P_{i}$
are the indecomposable projective
$\unicode[STIX]{x1D6F7}(T_{i})=P_{i}$
are the indecomposable projective
![]() $\unicode[STIX]{x1D6EC}$
-modules. Applying
$\unicode[STIX]{x1D6EC}$
-modules. Applying
![]() $\unicode[STIX]{x1D6F7}$
to
$\unicode[STIX]{x1D6F7}$
to
![]() $D^{\bullet }$
, we thus get a
$D^{\bullet }$
, we thus get a
![]() $P$
-resolution of
$P$
-resolution of
![]() $\unicode[STIX]{x1D6F7}(F)$
, so that
$\unicode[STIX]{x1D6F7}(F)$
, so that
![]() $\unicode[STIX]{x1D6F7}(F)$
is a
$\unicode[STIX]{x1D6F7}(F)$
is a
![]() $\unicode[STIX]{x1D6EC}$
-module. The resulting functor
$\unicode[STIX]{x1D6EC}$
-module. The resulting functor
![]() $\unicode[STIX]{x1D6F7}:\langle T\rangle \cap {\mathcal{A}}\rightarrow \text{mod}\text{-}\unicode[STIX]{x1D6EC}$
is exact as a functor between abelian categories (i.e., no derivation necessary) due to
$\unicode[STIX]{x1D6F7}:\langle T\rangle \cap {\mathcal{A}}\rightarrow \text{mod}\text{-}\unicode[STIX]{x1D6EC}$
is exact as a functor between abelian categories (i.e., no derivation necessary) due to
![]() $T$
partial tilting:
$T$
partial tilting:
![]() $\operatorname{RHom}(T,D^{\bullet })=\operatorname{Hom}(T,D^{\bullet })$
. It is essentially surjective as all projective modules are in the image:
$\operatorname{RHom}(T,D^{\bullet })=\operatorname{Hom}(T,D^{\bullet })$
. It is essentially surjective as all projective modules are in the image:
![]() $\unicode[STIX]{x1D6F7}(T_{i})=P_{i}$
.◻
$\unicode[STIX]{x1D6F7}(T_{i})=P_{i}$
.◻
1.2 Universal extensions
Let
![]() ${\mathcal{A}}$
be a (
${\mathcal{A}}$
be a (
![]() $\mathbf{k}$
-linear) abelian category with finite-dimensional
$\mathbf{k}$
-linear) abelian category with finite-dimensional
![]() $\operatorname{Ext}$
groups and
$\operatorname{Ext}$
groups and
![]() $D^{b}({\mathcal{A}})$
its bounded derived category, and fix two objects
$D^{b}({\mathcal{A}})$
its bounded derived category, and fix two objects
![]() $A,B\in {\mathcal{A}}$
. Following [Reference Hille and Perling7], we define the universal (co)extension of
$A,B\in {\mathcal{A}}$
. Following [Reference Hille and Perling7], we define the universal (co)extension of
![]() $B$
by
$B$
by
![]() $A$
by the short exact sequences
$A$
by the short exact sequences
where
![]() $r:=\dim \operatorname{Ext}^{1}(A,B)$
. Both extensions are given by the identity in
$r:=\dim \operatorname{Ext}^{1}(A,B)$
. Both extensions are given by the identity in
![]() $\operatorname{End}(\operatorname{Ext}^{1}(A,B))=\operatorname{Ext}^{1}(A,B)\otimes \operatorname{Ext}^{1}(A,B)^{\ast }$
, using
$\operatorname{End}(\operatorname{Ext}^{1}(A,B))=\operatorname{Ext}^{1}(A,B)\otimes \operatorname{Ext}^{1}(A,B)^{\ast }$
, using
The notation for the extensions is unambiguous because of universality. The following observations are straightforward computations [Reference Hille and Perling7]:
Lemma 1.4. Let
![]() $A,B\in {\mathcal{A}}$
and
$A,B\in {\mathcal{A}}$
and
![]() $\binom{A}{B^{r}}$
be their universal extension. If
$\binom{A}{B^{r}}$
be their universal extension. If
![]() $\operatorname{Ext}^{1}(B,B)=0$
, then
$\operatorname{Ext}^{1}(B,B)=0$
, then
![]() $\operatorname{Ext}^{1}(\binom{A}{B^{r}},B)=0$
. If
$\operatorname{Ext}^{1}(\binom{A}{B^{r}},B)=0$
. If
![]() $\operatorname{Ext}^{1}(A,A)=\operatorname{Ext}^{1}(B,A)=\operatorname{Ext}^{1}(B,B)=0$
, then
$\operatorname{Ext}^{1}(A,A)=\operatorname{Ext}^{1}(B,A)=\operatorname{Ext}^{1}(B,B)=0$
, then
![]() $\operatorname{Ext}^{1}(\binom{A}{B^{r}},\binom{A}{B^{r}})=0$
.
$\operatorname{Ext}^{1}(\binom{A}{B^{r}},\binom{A}{B^{r}})=0$
.
If
![]() $(A,B)$
is an exceptional pair with
$(A,B)$
is an exceptional pair with
![]() $\operatorname{Ext}^{{\geqslant}2}(A,B)=0$
, then
$\operatorname{Ext}^{{\geqslant}2}(A,B)=0$
, then
![]() $B\oplus \binom{A}{B^{r}}$
is partial tilting.
$B\oplus \binom{A}{B^{r}}$
is partial tilting.
An analogous statement holds for the coextensions, which leads to a partial tilting object
![]() $A\oplus \binom{A^{r}}{B}$
if
$A\oplus \binom{A^{r}}{B}$
if
![]() $(A,B)$
is an exceptional pair with
$(A,B)$
is an exceptional pair with
![]() $\operatorname{Ext}^{{\geqslant}2}(A,B)=0$
.
$\operatorname{Ext}^{{\geqslant}2}(A,B)=0$
.
This process can be iterated to yield the following statement which combines [Reference Hille and Perling7, Theorems 4.1 and 5.1]. Note that this source provides a slightly more general statement: instead of considering an exceptional sequence of objects of the abelian category
![]() ${\mathcal{A}}$
, one can take them from the derived category
${\mathcal{A}}$
, one can take them from the derived category
![]() ${\mathcal{D}}^{b}({\mathcal{A}})$
, under the assumption that also negative extensions vanish. Since in our treatment all exceptional objects come from
${\mathcal{D}}^{b}({\mathcal{A}})$
, under the assumption that also negative extensions vanish. Since in our treatment all exceptional objects come from
![]() ${\mathcal{A}}$
, we restrict to
${\mathcal{A}}$
, we restrict to
![]() $E_{i}\in {\mathcal{A}}$
right away.
$E_{i}\in {\mathcal{A}}$
right away.
Proposition 1.5. [Reference Hille and Perling7]
Let
![]() $(E_{1},\ldots ,E_{t})$
be an exceptional sequence in
$(E_{1},\ldots ,E_{t})$
be an exceptional sequence in
![]() ${\mathcal{D}}^{b}({\mathcal{A}})$
such that
${\mathcal{D}}^{b}({\mathcal{A}})$
such that
![]() $E_{i}\in {\mathcal{A}}$
and
$E_{i}\in {\mathcal{A}}$
and
![]() $\operatorname{Ext}^{{\geqslant}2}(E_{i},E_{j})=0$
for all
$\operatorname{Ext}^{{\geqslant}2}(E_{i},E_{j})=0$
for all
![]() $i,j$
. Then the object obtained from the sequence via iterated universal (co)extension is partial tilting.
$i,j$
. Then the object obtained from the sequence via iterated universal (co)extension is partial tilting.
Any exceptional sequence
![]() $(E_{1},\ldots ,E_{t})$
gives rise to an equivalence between the triangulated subcategory it generates,
$(E_{1},\ldots ,E_{t})$
gives rise to an equivalence between the triangulated subcategory it generates,
![]() $\langle E_{1},\ldots ,E_{t}\rangle$
and the derived category of the endomorphism differential graded (dg) algebra of
$\langle E_{1},\ldots ,E_{t}\rangle$
and the derived category of the endomorphism differential graded (dg) algebra of
![]() $\bigoplus E_{i}$
; see [Reference Keller11, Theorem 8.5(c)]. However, under the assumptions of Proposition 1.5, via (co)extensions we can avoid the dg algebra and deal with a finite-dimensional algebra instead.
$\bigoplus E_{i}$
; see [Reference Keller11, Theorem 8.5(c)]. However, under the assumptions of Proposition 1.5, via (co)extensions we can avoid the dg algebra and deal with a finite-dimensional algebra instead.
1.3 Special exceptional sequences and exact tilting objects
Let
![]() ${\mathcal{A}}$
be an abelian category and
${\mathcal{A}}$
be an abelian category and
![]() ${\mathcal{E}}=(E_{1},\ldots ,E_{t})$
be an exceptional sequence in
${\mathcal{E}}=(E_{1},\ldots ,E_{t})$
be an exceptional sequence in
![]() ${\mathcal{D}}^{b}({\mathcal{A}})$
. By abuse of notation, we write
${\mathcal{D}}^{b}({\mathcal{A}})$
. By abuse of notation, we write
![]() ${\mathcal{E}}$
rather than
${\mathcal{E}}$
rather than
![]() $\langle {\mathcal{E}}\rangle$
for the triangulated category generated by the sequence.
$\langle {\mathcal{E}}\rangle$
for the triangulated category generated by the sequence.
We consider sequences with the following properties:
 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}E_{i}\in {\mathcal{A}}\quad \text{for}~i=1,\ldots ,t,\quad \\ \operatorname{Ext}^{{\geqslant}2}(E_{i},E_{j})=0\quad \text{for}~i,j=1,\ldots ,t,\quad \\ \dim \operatorname{Hom}(E_{i},E_{j})\leqslant 1\quad \text{for}~i\leqslant j,\quad \\ \text{all non}\text{-}\text{zero maps}~E_{i}\rightarrow E_{j}~\text{are injective.}\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}E_{i}\in {\mathcal{A}}\quad \text{for}~i=1,\ldots ,t,\quad \\ \operatorname{Ext}^{{\geqslant}2}(E_{i},E_{j})=0\quad \text{for}~i,j=1,\ldots ,t,\quad \\ \dim \operatorname{Hom}(E_{i},E_{j})\leqslant 1\quad \text{for}~i\leqslant j,\quad \\ \text{all non}\text{-}\text{zero maps}~E_{i}\rightarrow E_{j}~\text{are injective.}\quad \end{array}\right.\end{eqnarray}$$
Proposition 1.6. Let
![]() $(E_{1},\ldots ,E_{t})$
be an exceptional sequence in
$(E_{1},\ldots ,E_{t})$
be an exceptional sequence in
![]() ${\mathcal{D}}^{b}({\mathcal{A}})$
satisfying (†), and let
${\mathcal{D}}^{b}({\mathcal{A}})$
satisfying (†), and let
![]() $T$
be its universal extension. Then
$T$
be its universal extension. Then
![]() $T$
is an exact partial tilting object.
$T$
is an exact partial tilting object.
Proof. We have to show that there are no nonsplitting surjections in
![]() $T$
. If
$T$
. If
![]() $\hom (E_{i},E_{j})=1$
for all
$\hom (E_{i},E_{j})=1$
for all
![]() $i\leqslant j$
, then the objects
$i\leqslant j$
, then the objects
![]() $E_{i}$
form a chain of unique inclusions
$E_{i}$
form a chain of unique inclusions
![]() $E_{1}\subsetneq E_{2}\subsetneq \cdots \,$
, and all image objects inside
$E_{1}\subsetneq E_{2}\subsetneq \cdots \,$
, and all image objects inside
![]() $E_{t}$
are fixed. In general, they form blocks of trees of such chains, and images in each sink are fixed.
$E_{t}$
are fixed. In general, they form blocks of trees of such chains, and images in each sink are fixed.
Now we check what happens when going to universal extensions: let
![]() $(A,B)$
be an exceptional pair of objects of
$(A,B)$
be an exceptional pair of objects of
![]() ${\mathcal{A}}$
with
${\mathcal{A}}$
with
![]() $\hom (A,B)=1$
,
$\hom (A,B)=1$
,
![]() $\operatorname{ext}^{1}(A,B)=r$
and
$\operatorname{ext}^{1}(A,B)=r$
and
![]() $\operatorname{ext}^{{\geqslant}2}(A,B)=0$
. The universal extension of the pair is
$\operatorname{ext}^{{\geqslant}2}(A,B)=0$
. The universal extension of the pair is
![]() $B\oplus E$
with
$B\oplus E$
with
![]() $E:=\binom{A}{B^{r}}$
, and from general theory we know
$E:=\binom{A}{B^{r}}$
, and from general theory we know
 $$\begin{eqnarray}\displaystyle \operatorname{Hom}(E,B)=\operatorname{Hom}(A,B) & \quad \;\Longrightarrow \;\quad & \displaystyle \text{Im}(E\rightarrow B)=A\subsetneq B,\nonumber\\ \displaystyle \operatorname{Hom}(B,E)=\operatorname{Ext}^{1}(A,B)^{\ast } & \quad \;\Longrightarrow \;\quad & \displaystyle \text{Im}(B\rightarrow E)\subset \binom{0}{B^{r}}\subsetneq \binom{A}{B^{r}}=E.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Hom}(E,B)=\operatorname{Hom}(A,B) & \quad \;\Longrightarrow \;\quad & \displaystyle \text{Im}(E\rightarrow B)=A\subsetneq B,\nonumber\\ \displaystyle \operatorname{Hom}(B,E)=\operatorname{Ext}^{1}(A,B)^{\ast } & \quad \;\Longrightarrow \;\quad & \displaystyle \text{Im}(B\rightarrow E)\subset \binom{0}{B^{r}}\subsetneq \binom{A}{B^{r}}=E.\nonumber\end{eqnarray}$$
Therefore surjections in
![]() $T$
only come from identity maps, and hence induce surjections under
$T$
only come from identity maps, and hence induce surjections under
![]() $\operatorname{Hom}(T_{i},-)$
.◻
$\operatorname{Hom}(T_{i},-)$
.◻
Proposition 1.7. Let
![]() ${\mathcal{A}}$
be an abelian category and
${\mathcal{A}}$
be an abelian category and
![]() ${\mathcal{E}}=(E_{1},\ldots ,E_{t})$
be an exceptional sequence in
${\mathcal{E}}=(E_{1},\ldots ,E_{t})$
be an exceptional sequence in
![]() ${\mathcal{D}}^{b}({\mathcal{A}})$
satisfying (†). Let
${\mathcal{D}}^{b}({\mathcal{A}})$
satisfying (†). Let
![]() $T$
be the iterated universal extension of
$T$
be the iterated universal extension of
![]() ${\mathcal{E}}$
, and let
${\mathcal{E}}$
, and let
![]() $\unicode[STIX]{x1D6EC}=\operatorname{End}(T)$
. Then the following categories are equivalent:
$\unicode[STIX]{x1D6EC}=\operatorname{End}(T)$
. Then the following categories are equivalent:
(1) the additive category
 ${\mathcal{E}}\cap {\mathcal{A}}$
;
${\mathcal{E}}\cap {\mathcal{A}}$
;(2) the abelian subcategory of
 ${\mathcal{A}}$
generated by
${\mathcal{A}}$
generated by
 $E_{1},\ldots ,E_{t}$
;
$E_{1},\ldots ,E_{t}$
;(3) the additive subcategory of
 ${\mathcal{A}}$
of objects admitting a filtration with factors
${\mathcal{A}}$
of objects admitting a filtration with factors
 $E_{1},E_{1}/E_{2},\ldots ,E_{t}/E_{t-1}$
;
$E_{1},E_{1}/E_{2},\ldots ,E_{t}/E_{t-1}$
;(4)
 $\text{mod}\text{-}\unicode[STIX]{x1D6EC}$
.
$\text{mod}\text{-}\unicode[STIX]{x1D6EC}$
.
Moreover,
![]() ${\mathcal{E}}\cong D^{b}({\mathcal{E}}\cap {\mathcal{A}})$
as triangulated categories.
${\mathcal{E}}\cong D^{b}({\mathcal{E}}\cap {\mathcal{A}})$
as triangulated categories.
Corollary 1.8. In particular,
![]() ${\mathcal{E}}\cap {\mathcal{A}}$
is an abelian category and has the object
${\mathcal{E}}\cap {\mathcal{A}}$
is an abelian category and has the object
![]() $T$
as a projective generator.
$T$
as a projective generator.
Corollary 1.9. The global dimensions of
![]() ${\mathcal{A}}$
, its subcategory
${\mathcal{A}}$
, its subcategory
![]() ${\mathcal{E}}\cap {\mathcal{A}}$
and the algebra
${\mathcal{E}}\cap {\mathcal{A}}$
and the algebra
![]() $\unicode[STIX]{x1D6EC}=\operatorname{End}(T)$
satisfy
$\unicode[STIX]{x1D6EC}=\operatorname{End}(T)$
satisfy
Proof of Corollary 1.9.
Comparing Ext groups in the two categories,
shows
![]() $\text{gl.dim}({\mathcal{E}}\cap {\mathcal{A}})\leqslant \text{gl.dim}({\mathcal{A}})$
, where the first equality of the chain uses
$\text{gl.dim}({\mathcal{E}}\cap {\mathcal{A}})\leqslant \text{gl.dim}({\mathcal{A}})$
, where the first equality of the chain uses
![]() ${\mathcal{D}}^{b}({\mathcal{E}}\cap {\mathcal{A}})={\mathcal{E}}$
, and the second relies on
${\mathcal{D}}^{b}({\mathcal{E}}\cap {\mathcal{A}})={\mathcal{E}}$
, and the second relies on
![]() ${\mathcal{E}}\subseteq {\mathcal{D}}^{b}({\mathcal{A}})$
being a full, triangulated subcategory. The equality of the corollary follows from the equivalence
${\mathcal{E}}\subseteq {\mathcal{D}}^{b}({\mathcal{A}})$
being a full, triangulated subcategory. The equality of the corollary follows from the equivalence
![]() $\text{mod}\text{-}\unicode[STIX]{x1D6EC}\cong {\mathcal{E}}\cap {\mathcal{A}}$
of Proposition 1.7.◻
$\text{mod}\text{-}\unicode[STIX]{x1D6EC}\cong {\mathcal{E}}\cap {\mathcal{A}}$
of Proposition 1.7.◻
Proof. Write
![]() ${\mathcal{C}}_{(1)},{\mathcal{C}}_{(2)},{\mathcal{C}}_{(3)},{\mathcal{C}}_{(4)}$
for the four categories of the theorem. We know from Proposition 1.3 that
${\mathcal{C}}_{(1)},{\mathcal{C}}_{(2)},{\mathcal{C}}_{(3)},{\mathcal{C}}_{(4)}$
for the four categories of the theorem. We know from Proposition 1.3 that
![]() ${\mathcal{C}}_{(1)}$
is an abelian category. Obviously, both
${\mathcal{C}}_{(1)}$
is an abelian category. Obviously, both
![]() ${\mathcal{C}}_{(1)}$
and
${\mathcal{C}}_{(1)}$
and
![]() ${\mathcal{C}}_{(2)}$
contain
${\mathcal{C}}_{(2)}$
contain
![]() $E_{1},\ldots ,E_{t}$
, hence
$E_{1},\ldots ,E_{t}$
, hence
![]() ${\mathcal{C}}_{(2)}\subseteq {\mathcal{C}}_{(1)}$
. On the other hand,
${\mathcal{C}}_{(2)}\subseteq {\mathcal{C}}_{(1)}$
. On the other hand,
![]() ${\mathcal{C}}_{(1)}$
is closed under kernels, cokernels and direct sums (all of these are special cases of distinguished triangles), so that
${\mathcal{C}}_{(1)}$
is closed under kernels, cokernels and direct sums (all of these are special cases of distinguished triangles), so that
![]() ${\mathcal{C}}_{(1)}\subseteq {\mathcal{C}}_{(2)}$
.
${\mathcal{C}}_{(1)}\subseteq {\mathcal{C}}_{(2)}$
.
For the equivalence of
![]() ${\mathcal{C}}_{(2)}\cong {\mathcal{C}}_{(3)}$
, we note that any module over a finite-dimensional algebra has a filtration by simple modules. The statement of (3) is that the objects
${\mathcal{C}}_{(2)}\cong {\mathcal{C}}_{(3)}$
, we note that any module over a finite-dimensional algebra has a filtration by simple modules. The statement of (3) is that the objects
![]() $E_{1},E_{2}/E_{1},\ldots ,E_{t}/E_{t-1}$
are the simples of the abelian category
$E_{1},E_{2}/E_{1},\ldots ,E_{t}/E_{t-1}$
are the simples of the abelian category
![]() ${\mathcal{C}}_{(2)}\cong \text{mod}\text{-}\unicode[STIX]{x1D6EC}$
.
${\mathcal{C}}_{(2)}\cong \text{mod}\text{-}\unicode[STIX]{x1D6EC}$
.
We get
![]() ${\mathcal{C}}_{(1)}\cong {\mathcal{C}}_{(4)}$
from Propositions 1.3 and 1.6.
${\mathcal{C}}_{(1)}\cong {\mathcal{C}}_{(4)}$
from Propositions 1.3 and 1.6.
The final statement follows from tilting theory, by Proposition 1.3 we have a commutative diagram whose horizontal arrows are equivalences:

Hence
![]() ${\mathcal{E}}\cong {\mathcal{D}}^{b}(\text{mod}\text{-}\unicode[STIX]{x1D6EC})\cong {\mathcal{D}}^{b}({\mathcal{E}}\cap {\mathcal{A}})$
, as claimed.◻
${\mathcal{E}}\cong {\mathcal{D}}^{b}(\text{mod}\text{-}\unicode[STIX]{x1D6EC})\cong {\mathcal{D}}^{b}({\mathcal{E}}\cap {\mathcal{A}})$
, as claimed.◻
Example 1.10. Both propositions fail if the condition
![]() $\hom (E_{i},E_{j})=1$
is removed from (†): the full and strong exceptional sequence
$\hom (E_{i},E_{j})=1$
is removed from (†): the full and strong exceptional sequence
![]() $({\mathcal{O}},{\mathcal{O}}(1))$
on
$({\mathcal{O}},{\mathcal{O}}(1))$
on
![]() ${\mathcal{D}}^{b}(\mathbb{P}^{1})$
satisfies
${\mathcal{D}}^{b}(\mathbb{P}^{1})$
satisfies
![]() ${\mathcal{O}},{\mathcal{O}}(1)\in \text{Coh}(\mathbb{P}^{1})$
and all nonzero morphisms
${\mathcal{O}},{\mathcal{O}}(1)\in \text{Coh}(\mathbb{P}^{1})$
and all nonzero morphisms
![]() ${\mathcal{O}}\rightarrow {\mathcal{O}}(1)$
are injective. However, the universal extension is just the direct sum
${\mathcal{O}}\rightarrow {\mathcal{O}}(1)$
are injective. However, the universal extension is just the direct sum
![]() ${\mathcal{O}}\oplus {\mathcal{O}}(1)$
, and this bundle is not exact tilting, due to the nonsplit surjection
${\mathcal{O}}\oplus {\mathcal{O}}(1)$
, and this bundle is not exact tilting, due to the nonsplit surjection
![]() ${\mathcal{O}}^{2}{\twoheadrightarrow}{\mathcal{O}}(1)$
.
${\mathcal{O}}^{2}{\twoheadrightarrow}{\mathcal{O}}(1)$
.
2 Chains of negative curves
Let
![]() $X$
be a smooth, projective surface. In order to apply the theory of exceptional sequences and tilting, we assume that line bundles on
$X$
be a smooth, projective surface. In order to apply the theory of exceptional sequences and tilting, we assume that line bundles on
![]() $X$
are exceptional. This property is equivalent to
$X$
are exceptional. This property is equivalent to
![]() $q(X)=p_{g}(X)=0$
, that is vanishing irregularity (
$q(X)=p_{g}(X)=0$
, that is vanishing irregularity (
![]() $q(X)=h^{1}({\mathcal{O}}_{X})=0$
) and vanishing geometric genus (
$q(X)=h^{1}({\mathcal{O}}_{X})=0$
) and vanishing geometric genus (
![]() $p_{g}(X)=h^{0}(\unicode[STIX]{x1D714}_{X})=h^{2}({\mathcal{O}}_{X})^{\ast }=0$
). It holds for rational, for example toric surfaces, but in fact, in any Kodaira dimension there are surfaces with
$p_{g}(X)=h^{0}(\unicode[STIX]{x1D714}_{X})=h^{2}({\mathcal{O}}_{X})^{\ast }=0$
). It holds for rational, for example toric surfaces, but in fact, in any Kodaira dimension there are surfaces with
![]() $q=p_{g}=0$
; see [Reference Barth, Hulek, Peters and Van de Ven3, Sections VII.11, VIII.15]. Throughout, we assume:
$q=p_{g}=0$
; see [Reference Barth, Hulek, Peters and Van de Ven3, Sections VII.11, VIII.15]. Throughout, we assume:
From now on we fix a chain
![]() $(C_{1},\ldots ,C_{t})$
of type
$(C_{1},\ldots ,C_{t})$
of type
![]() $A$
of smooth, rational curves in
$A$
of smooth, rational curves in
![]() $X$
, that is the curves are pairwise disjoint except that
$X$
, that is the curves are pairwise disjoint except that
![]() $C_{i}$
and
$C_{i}$
and
![]() $C_{i+1}$
intersect transversally in a single point, for
$C_{i+1}$
intersect transversally in a single point, for
![]() $i=1,\ldots ,t-1$
.
$i=1,\ldots ,t-1$
.
We consider the sequence of line bundles (note that it starts at
![]() $E_{0}$
)
$E_{0}$
)
Lemma 2.1. The sequence of line bundles
![]() ${\mathcal{E}}$
is an exceptional sequence.
${\mathcal{E}}$
is an exceptional sequence.
If
![]() $C_{i}^{2}\leqslant -2$
for all
$C_{i}^{2}\leqslant -2$
for all
![]() $i$
, then this sequence satisfies assumption (†).
$i$
, then this sequence satisfies assumption (†).
Proof. By our standing assumption that line bundles on
![]() $X$
are exceptional, all
$X$
are exceptional, all
![]() $E_{i}$
are exceptional sheaves. Furthermore, for a subchain
$E_{i}$
are exceptional sheaves. Furthermore, for a subchain
![]() $D$
of
$D$
of
![]() $C_{1}\cup \cdots \cup C_{t}$
, the long cohomology sequence for the short exact sequence
$C_{1}\cup \cdots \cup C_{t}$
, the long cohomology sequence for the short exact sequence
![]() $0\rightarrow {\mathcal{O}}(-D)\rightarrow {\mathcal{O}}\rightarrow {\mathcal{O}}_{D}\rightarrow 0$
implies
$0\rightarrow {\mathcal{O}}(-D)\rightarrow {\mathcal{O}}\rightarrow {\mathcal{O}}_{D}\rightarrow 0$
implies
![]() $H^{\ast }({\mathcal{O}}(-D))=0$
. Here we use that all components of
$H^{\ast }({\mathcal{O}}(-D))=0$
. Here we use that all components of
![]() $D$
are rational, that
$D$
are rational, that
![]() $D$
is reduced and connected (hence
$D$
is reduced and connected (hence
![]() $H^{0}({\mathcal{O}}_{D})=\mathbf{k}$
), and that
$H^{0}({\mathcal{O}}_{D})=\mathbf{k}$
), and that
![]() ${\mathcal{O}}$
is exceptional. For any
${\mathcal{O}}$
is exceptional. For any
![]() $i>j$
, we have
$i>j$
, we have
![]() $\operatorname{Ext}^{k}(E_{i},E_{j})=H^{k}({\mathcal{O}}(-D))$
for a divisor
$\operatorname{Ext}^{k}(E_{i},E_{j})=H^{k}({\mathcal{O}}(-D))$
for a divisor
![]() $D$
of that type. Hence the sequence is exceptional.
$D$
of that type. Hence the sequence is exceptional.
As
![]() ${\mathcal{E}}$
is a chain of line bundles, all nonzero maps
${\mathcal{E}}$
is a chain of line bundles, all nonzero maps
![]() $E_{i}\rightarrow E_{j}$
are inclusions. The sequence has vanishing
$E_{i}\rightarrow E_{j}$
are inclusions. The sequence has vanishing
![]() $\operatorname{Ext}^{2}$
for general reasons: for any
$\operatorname{Ext}^{2}$
for general reasons: for any
![]() $i\leqslant j$
, we have
$i\leqslant j$
, we have
![]() $\operatorname{Ext}^{2}(E_{i},E_{j})=H^{2}({\mathcal{O}}(D))$
for a subchain
$\operatorname{Ext}^{2}(E_{i},E_{j})=H^{2}({\mathcal{O}}(D))$
for a subchain
![]() $D$
as above. The short exact sequence
$D$
as above. The short exact sequence
![]() $0\rightarrow {\mathcal{O}}\rightarrow {\mathcal{O}}(D)\rightarrow {\mathcal{O}}_{D}(D)\rightarrow 0$
induces
$0\rightarrow {\mathcal{O}}\rightarrow {\mathcal{O}}(D)\rightarrow {\mathcal{O}}_{D}(D)\rightarrow 0$
induces
![]() $H^{2}({\mathcal{O}}(D))=0$
, using that
$H^{2}({\mathcal{O}}(D))=0$
, using that
![]() ${\mathcal{O}}$
is exceptional and that
${\mathcal{O}}$
is exceptional and that
![]() ${\mathcal{O}}_{D}(D)$
has 1-dimensional support.
${\mathcal{O}}_{D}(D)$
has 1-dimensional support.
We proceed to check
![]() $\dim \operatorname{Hom}(E_{i},E_{j})=1$
for
$\dim \operatorname{Hom}(E_{i},E_{j})=1$
for
![]() $i\leqslant j$
. This is the place where we use the assumption
$i\leqslant j$
. This is the place where we use the assumption
![]() $C_{i}^{2}\leqslant -2$
. Note that
$C_{i}^{2}\leqslant -2$
. Note that
![]() $\operatorname{Hom}(E_{i},E_{j})=H^{0}({\mathcal{O}}(D))$
for a subchain
$\operatorname{Hom}(E_{i},E_{j})=H^{0}({\mathcal{O}}(D))$
for a subchain
![]() $D$
of
$D$
of
![]() $C_{1}\cup \cdots \cup C_{t}$
. If
$C_{1}\cup \cdots \cup C_{t}$
. If
![]() $D$
is irreducible, that is
$D$
is irreducible, that is
![]() $j=i+1$
, then we get
$j=i+1$
, then we get
![]() $H^{0}({\mathcal{O}}(D))=\mathbf{k}$
from the cohomology sequence of
$H^{0}({\mathcal{O}}(D))=\mathbf{k}$
from the cohomology sequence of
![]() $0\rightarrow {\mathcal{O}}\rightarrow {\mathcal{O}}(D)\rightarrow {\mathcal{O}}_{D}(D)\rightarrow 0$
using
$0\rightarrow {\mathcal{O}}\rightarrow {\mathcal{O}}(D)\rightarrow {\mathcal{O}}_{D}(D)\rightarrow 0$
using
![]() ${\mathcal{O}}_{D}(D)={\mathcal{O}}_{\mathbb{P}^{1}}(m)$
with
${\mathcal{O}}_{D}(D)={\mathcal{O}}_{\mathbb{P}^{1}}(m)$
with
![]() $m=D^{2}<0$
. Now, by induction, assume that we know
$m=D^{2}<0$
. Now, by induction, assume that we know
![]() $H^{0}({\mathcal{O}}(D))=\mathbf{k}$
for some chain and let
$H^{0}({\mathcal{O}}(D))=\mathbf{k}$
for some chain and let
![]() $C$
be a curve meeting
$C$
be a curve meeting
![]() $D$
. We consider the short exact sequence
$D$
. We consider the short exact sequence
We have
![]() $H^{0}({\mathcal{O}}_{C}(C+D))=H^{0}({\mathcal{O}}_{\mathbb{P}^{1}}(C^{2}+1))=0$
, since
$H^{0}({\mathcal{O}}_{C}(C+D))=H^{0}({\mathcal{O}}_{\mathbb{P}^{1}}(C^{2}+1))=0$
, since
![]() $C$
meets precisely one component of
$C$
meets precisely one component of
![]() $D$
and
$D$
and
![]() $C^{2}+1<0$
. Taking global sections thus gives
$C^{2}+1<0$
. Taking global sections thus gives
![]() $H^{0}({\mathcal{O}}(D+C))=H^{0}({\mathcal{O}}(D))=\mathbf{k}$
by induction.◻
$H^{0}({\mathcal{O}}(D+C))=H^{0}({\mathcal{O}}(D))=\mathbf{k}$
by induction.◻
Remark 2.2. The proof shows a little more: if just one curve has self-intersection
![]() $-1$
and all others satisfy
$-1$
and all others satisfy
![]() $C_{i}^{2}\leqslant -2$
, then (†) still holds.
$C_{i}^{2}\leqslant -2$
, then (†) still holds.
Even more than one
![]() $(-1)$
-curve can be supported in certain cases. For instance, it can be checked that a
$(-1)$
-curve can be supported in certain cases. For instance, it can be checked that a
![]() $(-1)(-3)(-1)$
-chain satisfies (†), but a
$(-1)(-3)(-1)$
-chain satisfies (†), but a
![]() $(-1)(-2)(-1)$
-chain does not. Note that the former chain contracts to a
$(-1)(-2)(-1)$
-chain does not. Note that the former chain contracts to a
![]() $(-1)$
-curve, whereas the latter contracts to a 0-curve.
$(-1)$
-curve, whereas the latter contracts to a 0-curve.
Remark 2.3. We now consider the case of two
![]() $(-1)$
-curves and show that condition (†) fails: if
$(-1)$
-curves and show that condition (†) fails: if
![]() $C_{1}$
and
$C_{1}$
and
![]() $C_{2}$
are
$C_{2}$
are
![]() $(-1)$
-curves intersecting in a point, then
$(-1)$
-curves intersecting in a point, then
![]() $({\mathcal{O}}(-C_{1}-C_{2}),{\mathcal{O}}(-C_{1}),{\mathcal{O}})$
is a strong exceptional sequence with
$({\mathcal{O}}(-C_{1}-C_{2}),{\mathcal{O}}(-C_{1}),{\mathcal{O}})$
is a strong exceptional sequence with
![]() $\dim \operatorname{Hom}({\mathcal{O}}(-C_{1}-C_{2}),{\mathcal{O}})=2$
.
$\dim \operatorname{Hom}({\mathcal{O}}(-C_{1}-C_{2}),{\mathcal{O}})=2$
.
Blowing down
![]() $C_{1}$
yields
$C_{1}$
yields
![]() $\unicode[STIX]{x1D70B}:X\rightarrow Y$
with a smooth, rational curve
$\unicode[STIX]{x1D70B}:X\rightarrow Y$
with a smooth, rational curve
![]() $F\subset Y$
such that
$F\subset Y$
such that
![]() $F^{2}=0$
. Assume that
$F^{2}=0$
. Assume that
![]() $F$
is the fiber of a morphism
$F$
is the fiber of a morphism
![]() $p:Y\rightarrow \mathbb{P}^{1}$
, for example if
$p:Y\rightarrow \mathbb{P}^{1}$
, for example if
![]() $X$
is a Hirzebruch surface. Hence
$X$
is a Hirzebruch surface. Hence
![]() ${\mathcal{O}}(C_{1}+C_{2})=\unicode[STIX]{x1D70B}^{\ast }{\mathcal{O}}(F)=\unicode[STIX]{x1D70B}^{\ast }p^{\ast }{\mathcal{O}}_{\mathbb{P}^{1}}(z)$
for a point
${\mathcal{O}}(C_{1}+C_{2})=\unicode[STIX]{x1D70B}^{\ast }{\mathcal{O}}(F)=\unicode[STIX]{x1D70B}^{\ast }p^{\ast }{\mathcal{O}}_{\mathbb{P}^{1}}(z)$
for a point
![]() $z$
on
$z$
on
![]() $\mathbb{P}^{1}$
. Pulling back the surjection
$\mathbb{P}^{1}$
. Pulling back the surjection
![]() ${\mathcal{O}}_{\mathbb{P}^{1}}^{2}{\twoheadrightarrow}{\mathcal{O}}_{\mathbb{P}^{1}}(z)$
gives
${\mathcal{O}}_{\mathbb{P}^{1}}^{2}{\twoheadrightarrow}{\mathcal{O}}_{\mathbb{P}^{1}}(z)$
gives
![]() ${\mathcal{O}}_{X}^{2}{\twoheadrightarrow}{\mathcal{O}}_{X}(C_{1}+C_{2})$
. Hence the partial tilting bundle
${\mathcal{O}}_{X}^{2}{\twoheadrightarrow}{\mathcal{O}}_{X}(C_{1}+C_{2})$
. Hence the partial tilting bundle
![]() $T={\mathcal{O}}(-C_{1}-C_{2})\oplus {\mathcal{O}}(-C_{1})\oplus {\mathcal{O}}$
is not exact.
$T={\mathcal{O}}(-C_{1}-C_{2})\oplus {\mathcal{O}}(-C_{1})\oplus {\mathcal{O}}$
is not exact.
Likewise, it can be shown that the functor
![]() $\operatorname{Hom}(T,-)$
does not induce an equivalence of abelian categories.
$\operatorname{Hom}(T,-)$
does not induce an equivalence of abelian categories.
The exceptional sequence
![]() ${\mathcal{E}}=({\mathcal{O}}(-C_{1}-\cdots -C_{t}),\ldots ,{\mathcal{O}}(-C_{1}),{\mathcal{O}})$
is strong precisely when all
${\mathcal{E}}=({\mathcal{O}}(-C_{1}-\cdots -C_{t}),\ldots ,{\mathcal{O}}(-C_{1}),{\mathcal{O}})$
is strong precisely when all
![]() $C_{i}^{2}\geqslant -1$
. By contrast, we are interested in the case
$C_{i}^{2}\geqslant -1$
. By contrast, we are interested in the case
![]() $C_{i}^{2}<-1$
. One motivation for studying the triangulated category
$C_{i}^{2}<-1$
. One motivation for studying the triangulated category
![]() ${\mathcal{E}}$
generated by such line bundles is that it contains the torsion sheaves
${\mathcal{E}}$
generated by such line bundles is that it contains the torsion sheaves
![]() ${\mathcal{O}}_{C_{1}},{\mathcal{O}}_{C_{2}}(-1),\ldots ,{\mathcal{O}}_{C_{t}}(-1)$
. These are of particular interest when all
${\mathcal{O}}_{C_{1}},{\mathcal{O}}_{C_{2}}(-1),\ldots ,{\mathcal{O}}_{C_{t}}(-1)$
. These are of particular interest when all
![]() $C_{i}^{2}=-2$
, for in that case they form an
$C_{i}^{2}=-2$
, for in that case they form an
![]() $A_{t}$
-chain of spherical sheaves and thus give a braid group action on
$A_{t}$
-chain of spherical sheaves and thus give a braid group action on
![]() ${\mathcal{D}}^{b}(X)$
. In [Reference Ishii and Uehara9], the full subcategory
${\mathcal{D}}^{b}(X)$
. In [Reference Ishii and Uehara9], the full subcategory
![]() ${\mathcal{D}}_{C}^{b}(X)\subset {\mathcal{D}}^{b}(X)$
of objects supported on the subvariety
${\mathcal{D}}_{C}^{b}(X)\subset {\mathcal{D}}^{b}(X)$
of objects supported on the subvariety
![]() $C:=C_{1}\cup \cdots \cup C_{t}$
is studied. The category
$C:=C_{1}\cup \cdots \cup C_{t}$
is studied. The category
![]() ${\mathcal{E}}$
of this article contains some of the spherical sheaves (one for each irreducible component) but has the advantage of being generated by an exceptional sequence. This allows access to methods from representation theory. We think of
${\mathcal{E}}$
of this article contains some of the spherical sheaves (one for each irreducible component) but has the advantage of being generated by an exceptional sequence. This allows access to methods from representation theory. We think of
![]() ${\mathcal{E}}$
as a categorical neighborhood of the triangulated category generated by
${\mathcal{E}}$
as a categorical neighborhood of the triangulated category generated by
![]() ${\mathcal{O}}_{C_{1}},{\mathcal{O}}_{C_{2}}(-1),\ldots ,{\mathcal{O}}_{C_{t}}(-1)$
.
${\mathcal{O}}_{C_{1}},{\mathcal{O}}_{C_{2}}(-1),\ldots ,{\mathcal{O}}_{C_{t}}(-1)$
.
Example 2.4. We take up the example from the introduction. Let
![]() ${\mathcal{P}}$
and
${\mathcal{P}}$
and
![]() ${\mathcal{I}}$
be the partial tilting bundles obtained from universal extension and coextension, respectively. For
${\mathcal{I}}$
be the partial tilting bundles obtained from universal extension and coextension, respectively. For
![]() $t=1$
, these are
$t=1$
, these are
Of these,
![]() ${\mathcal{P}}$
is exact partial tilting but
${\mathcal{P}}$
is exact partial tilting but
![]() ${\mathcal{I}}$
is not—observe that
${\mathcal{I}}$
is not—observe that
![]() ${\mathcal{I}}$
contains the nonsplitting surjections
${\mathcal{I}}$
contains the nonsplitting surjections
![]() $\binom{{\mathcal{O}}(-C)^{r}}{{\mathcal{O}}}{\twoheadrightarrow}{\mathcal{O}}(-C)$
. For
$\binom{{\mathcal{O}}(-C)^{r}}{{\mathcal{O}}}{\twoheadrightarrow}{\mathcal{O}}(-C)$
. For
![]() $r=1$
, that is a single
$r=1$
, that is a single
![]() $(-2)$
-curve, the endomorphism algebras are the same:
$(-2)$
-curve, the endomorphism algebras are the same:
![]() $\operatorname{End}({\mathcal{P}})=\operatorname{End}({\mathcal{I}})$
.
$\operatorname{End}({\mathcal{P}})=\operatorname{End}({\mathcal{I}})$
.
The object
![]() ${\mathcal{P}}$
is a projective generator, but
${\mathcal{P}}$
is a projective generator, but
![]() ${\mathcal{I}}$
is in general not an injective cogenerator (it is an injective cogenerator for the category of
${\mathcal{I}}$
is in general not an injective cogenerator (it is an injective cogenerator for the category of
![]() $\unicode[STIX]{x1D6E5}$
-modules).
$\unicode[STIX]{x1D6E5}$
-modules).
Next, we spell out what Lemma 2.1 implies in view of Propositions 1.3, 1.6, 1.7. Note that the sheaves in (3) below are the minimal line bundle and the torsion sheaves supported on the irreducible components of the chain. Therefore, these are the simple objects of the abelian category
![]() $\text{Coh}_{{\mathcal{E}}}(X)\,:=\text{Coh}(X)\cap {\mathcal{E}}$
. Also note that the structure sheaf
$\text{Coh}_{{\mathcal{E}}}(X)\,:=\text{Coh}(X)\cap {\mathcal{E}}$
. Also note that the structure sheaf
![]() ${\mathcal{O}}$
, that is the maximal line bundle of the sequence is the consecutive extension of these torsion sheaves by
${\mathcal{O}}$
, that is the maximal line bundle of the sequence is the consecutive extension of these torsion sheaves by
![]() ${\mathcal{O}}(-C_{1}-\cdots -C_{t})$
.
${\mathcal{O}}(-C_{1}-\cdots -C_{t})$
.
Theorem 2.5. Let
![]() $C_{1},\ldots ,C_{t}$
be an
$C_{1},\ldots ,C_{t}$
be an
![]() $A_{t}$
-chain of curves on
$A_{t}$
-chain of curves on
![]() $X$
such that
$X$
such that
![]() $C_{i}\cong \mathbb{P}^{1}$
and
$C_{i}\cong \mathbb{P}^{1}$
and
![]() $C_{i}^{2}\leqslant -2$
for all
$C_{i}^{2}\leqslant -2$
for all
![]() $i$
, let
$i$
, let
![]() $T$
be the universal extension of the sequence
$T$
be the universal extension of the sequence
and let
![]() $\unicode[STIX]{x1D6EC}=\operatorname{End}(T)$
be the endomorphism algebra. Then
$\unicode[STIX]{x1D6EC}=\operatorname{End}(T)$
be the endomorphism algebra. Then
![]() $T$
is an exact partial tilting object and induces an equivalence of abelian categories
$T$
is an exact partial tilting object and induces an equivalence of abelian categories
Furthermore, the following categories are equivalent to each other:
(1) the additive category
 $\text{Coh}_{{\mathcal{E}}}(X):={\mathcal{E}}\cap \text{Coh}(X)$
;
$\text{Coh}_{{\mathcal{E}}}(X):={\mathcal{E}}\cap \text{Coh}(X)$
;(2) the abelian subcategory of
 $\text{Coh}(X)$
generated by the line bundles
$\text{Coh}(X)$
generated by the line bundles
 ${\mathcal{O}}(-C_{1}\cdots -C_{t}),\ldots ,{\mathcal{O}}(-C_{1}),{\mathcal{O}}$
;
${\mathcal{O}}(-C_{1}\cdots -C_{t}),\ldots ,{\mathcal{O}}(-C_{1}),{\mathcal{O}}$
;(3) the additive category of coherent sheaves admitting a filtration with factors
 ${\mathcal{O}}_{X}(-C_{1}\cdots -C_{t}),{\mathcal{O}}_{C_{t}}(-1),\ldots ,{\mathcal{O}}_{C_{2}}(-1),{\mathcal{O}}_{C_{1}}$
.
${\mathcal{O}}_{X}(-C_{1}\cdots -C_{t}),{\mathcal{O}}_{C_{t}}(-1),\ldots ,{\mathcal{O}}_{C_{2}}(-1),{\mathcal{O}}_{C_{1}}$
.
Moreover,
![]() ${\mathcal{E}}\cong {\mathcal{D}}^{b}(\text{Coh}_{{\mathcal{E}}}(X))$
as triangulated categories and the algebra
${\mathcal{E}}\cong {\mathcal{D}}^{b}(\text{Coh}_{{\mathcal{E}}}(X))$
as triangulated categories and the algebra
![]() $\unicode[STIX]{x1D6EC}$
is quasi-hereditary.
$\unicode[STIX]{x1D6EC}$
is quasi-hereditary.
Proof. By Lemma 2.1, the sequence of line bundles
![]() ${\mathcal{E}}$
is an exceptional sequence satisfying the condition (†). Hence by Proposition 1.6, the universal extension
${\mathcal{E}}$
is an exceptional sequence satisfying the condition (†). Hence by Proposition 1.6, the universal extension
![]() $T$
of
$T$
of
![]() ${\mathcal{E}}$
is an exact tilting object and we get the equivalence of abelian categories
${\mathcal{E}}$
is an exact tilting object and we get the equivalence of abelian categories
![]() $\operatorname{RHom}(T,-):\text{Coh}_{{\mathcal{E}}}(X)\stackrel{{\sim}}{\longrightarrow }\text{mod}\text{-}\unicode[STIX]{x1D6EC}$
from Proposition 1.3.
$\operatorname{RHom}(T,-):\text{Coh}_{{\mathcal{E}}}(X)\stackrel{{\sim}}{\longrightarrow }\text{mod}\text{-}\unicode[STIX]{x1D6EC}$
from Proposition 1.3.
The properties of the abelian category follow from Proposition 1.7, using that the inclusion
![]() ${\mathcal{O}}(-C_{1}\cdots -C_{i-1}){\hookrightarrow}{\mathcal{O}}(-C_{1}-\cdots -C_{i})$
has cokernel
${\mathcal{O}}(-C_{1}\cdots -C_{i-1}){\hookrightarrow}{\mathcal{O}}(-C_{1}-\cdots -C_{i})$
has cokernel
![]() ${\mathcal{O}}_{C_{i}}(-1)$
, for
${\mathcal{O}}_{C_{i}}(-1)$
, for
![]() $i>1$
.
$i>1$
.
As
![]() $X$
is a smooth surface,
$X$
is a smooth surface,
![]() $\text{Coh}(X)$
has global dimension 2. Therefore, the category
$\text{Coh}(X)$
has global dimension 2. Therefore, the category
![]() $\text{Coh}_{{\mathcal{E}}}(X)$
also has global dimension 2, and hence so has the algebra
$\text{Coh}_{{\mathcal{E}}}(X)$
also has global dimension 2, and hence so has the algebra
![]() $\unicode[STIX]{x1D6EC}$
. It is a general fact that this already implies
$\unicode[STIX]{x1D6EC}$
. It is a general fact that this already implies
![]() $\unicode[STIX]{x1D6EC}$
quasi-hereditary [Reference Dlab and Ringel5, Theorem 2].◻
$\unicode[STIX]{x1D6EC}$
quasi-hereditary [Reference Dlab and Ringel5, Theorem 2].◻
3 First properties of the abelian category
 $\text{Coh}_{{\mathcal{E}}}(X)$
$\text{Coh}_{{\mathcal{E}}}(X)$
Lemma 3.1.
(1) A torsion free sheaf in
 $\text{Coh}_{{\mathcal{E}}}(X)$
is locally free.
$\text{Coh}_{{\mathcal{E}}}(X)$
is locally free.(2)
 $\text{Coh}_{{\mathcal{E}}}(X)$
is closed under taking torsion subsheaves.
$\text{Coh}_{{\mathcal{E}}}(X)$
is closed under taking torsion subsheaves.(3)
 $F\in \text{Coh}_{{\mathcal{E}}}(X)$
is locally free
$F\in \text{Coh}_{{\mathcal{E}}}(X)$
is locally free
 $\;\Longleftrightarrow \;$
$\;\Longleftrightarrow \;$
 $\operatorname{Ext}^{2}(F,-)=0$
on
$\operatorname{Ext}^{2}(F,-)=0$
on
 $\text{Coh}_{{\mathcal{E}}}(X)$
.
$\text{Coh}_{{\mathcal{E}}}(X)$
.(4) The support of a nonzero object in
 ${\mathcal{E}}$
is either
${\mathcal{E}}$
is either
 $X$
or a union of curves
$X$
or a union of curves
 $C_{i}$
.
$C_{i}$
.
Proof. (1) By characterization (3) of Theorem 2.5, a sheaf
![]() $F\in \text{Coh}_{{\mathcal{E}}}(X)$
has a filtration
$F\in \text{Coh}_{{\mathcal{E}}}(X)$
has a filtration
![]() $0=F^{0}\subsetneq F^{1}\subsetneq \cdots \subsetneq F^{l}=F$
, whose factors
$0=F^{0}\subsetneq F^{1}\subsetneq \cdots \subsetneq F^{l}=F$
, whose factors
![]() $F^{i}/F^{i-1}$
are either the torsion sheaves
$F^{i}/F^{i-1}$
are either the torsion sheaves
![]() ${\mathcal{O}}_{C_{1}},{\mathcal{O}}_{C_{2}}(-1),\ldots ,{\mathcal{O}}_{C_{t}}(-1)$
or the line bundle
${\mathcal{O}}_{C_{1}},{\mathcal{O}}_{C_{2}}(-1),\ldots ,{\mathcal{O}}_{C_{t}}(-1)$
or the line bundle
![]() ${\mathcal{O}}(-C_{1}\cdots -C_{t})$
. We claim that for
${\mathcal{O}}(-C_{1}\cdots -C_{t})$
. We claim that for
![]() $F$
indecomposable this filtration is a refinement of the torsion filtration of
$F$
indecomposable this filtration is a refinement of the torsion filtration of
![]() $F$
: the torsion part of
$F$
: the torsion part of
![]() $F$
is the maximal
$F$
is the maximal
![]() $F^{i}$
such that all factors up to
$F^{i}$
such that all factors up to
![]() $F^{i}$
are torsion.
$F^{i}$
are torsion.
For this, consider a nonsplit extension
![]() $0\rightarrow M^{\prime }\rightarrow M\rightarrow M^{\prime \prime }\rightarrow 0$
of sheaves on
$0\rightarrow M^{\prime }\rightarrow M\rightarrow M^{\prime \prime }\rightarrow 0$
of sheaves on
![]() $X$
with
$X$
with
![]() $M^{\prime }$
locally free, and
$M^{\prime }$
locally free, and
![]() $M^{\prime \prime }$
indecomposable and purely 1-dimensional (i.e., supported on a divisor without embedded points). Then the sheaf
$M^{\prime \prime }$
indecomposable and purely 1-dimensional (i.e., supported on a divisor without embedded points). Then the sheaf
![]() $M$
is locally free: by assumption, the homological dimensions are
$M$
is locally free: by assumption, the homological dimensions are
![]() $\text{hd}(M^{\prime \prime })=1$
and
$\text{hd}(M^{\prime \prime })=1$
and
![]() $\text{hd}(M^{\prime })=0$
; as the extension does not split, this implies
$\text{hd}(M^{\prime })=0$
; as the extension does not split, this implies
![]() $\text{hd}(M)=0$
. (Recall the homological dimension
$\text{hd}(M)=0$
. (Recall the homological dimension
![]() $\text{hd}(M)=\sup _{x\in X}\text{pd}(M_{x})$
, the supremum of projective dimensions of stalks of a sheaf
$\text{hd}(M)=\sup _{x\in X}\text{pd}(M_{x})$
, the supremum of projective dimensions of stalks of a sheaf
![]() $M$
. The local situation is
$M$
. The local situation is
![]() $0\rightarrow R^{r}\rightarrow M\rightarrow R/f\rightarrow 0$
for a 2-dimensional regular local ring
$0\rightarrow R^{r}\rightarrow M\rightarrow R/f\rightarrow 0$
for a 2-dimensional regular local ring
![]() $R$
and
$R$
and
![]() $0\neq f\in R$
.)
$0\neq f\in R$
.)
This also shows (2) and (4), that is that
![]() $\text{Coh}_{{\mathcal{E}}}(X)$
is closed under taking torsion subsheaves, and sheaves in
$\text{Coh}_{{\mathcal{E}}}(X)$
is closed under taking torsion subsheaves, and sheaves in
![]() $\text{Coh}_{{\mathcal{E}}}(X)$
have the supports mentioned in (4). This property immediately extends to objects of
$\text{Coh}_{{\mathcal{E}}}(X)$
have the supports mentioned in (4). This property immediately extends to objects of
![]() ${\mathcal{E}}$
.
${\mathcal{E}}$
.
(3) Let
![]() $V\in \text{Coh}_{{\mathcal{E}}}(X)$
be locally free. Again by Theorem 2.5,
$V\in \text{Coh}_{{\mathcal{E}}}(X)$
be locally free. Again by Theorem 2.5,
![]() $V$
has a filtration by the line bundles occurring in the exceptional sequence
$V$
has a filtration by the line bundles occurring in the exceptional sequence
![]() ${\mathcal{E}}$
. (Note that if
${\mathcal{E}}$
. (Note that if
![]() $E_{i}\subset V$
, then
$E_{i}\subset V$
, then
![]() $V/E_{i}$
is torsion free, hence locally free again.) Therefore, showing
$V/E_{i}$
is torsion free, hence locally free again.) Therefore, showing
![]() $\operatorname{Ext}^{2}(V,-)=0$
reduces to showing
$\operatorname{Ext}^{2}(V,-)=0$
reduces to showing
![]() $\operatorname{Ext}^{2}(E_{i},-)=0$
, but the latter vanishing is clear from the outset.
$\operatorname{Ext}^{2}(E_{i},-)=0$
, but the latter vanishing is clear from the outset.
For the converse, assume
![]() $\operatorname{Ext}^{2}(F,-)=0$
and let
$\operatorname{Ext}^{2}(F,-)=0$
and let
![]() $0\rightarrow F^{\prime }\rightarrow F\rightarrow F^{\prime \prime }\rightarrow 0$
be the torsion decomposition of
$0\rightarrow F^{\prime }\rightarrow F\rightarrow F^{\prime \prime }\rightarrow 0$
be the torsion decomposition of
![]() $F$
, that is
$F$
, that is
![]() $F^{\prime }$
is the maximal torsion subsheaf of
$F^{\prime }$
is the maximal torsion subsheaf of
![]() $F$
. For any
$F$
. For any
![]() $A\in \text{Coh}_{{\mathcal{E}}}(X)$
, we get an exact sequence
$A\in \text{Coh}_{{\mathcal{E}}}(X)$
, we get an exact sequence
![]() $0=\operatorname{Ext}^{2}(F,A)\rightarrow \operatorname{Ext}^{2}(F^{\prime },A)\rightarrow 0$
. Especially for
$0=\operatorname{Ext}^{2}(F,A)\rightarrow \operatorname{Ext}^{2}(F^{\prime },A)\rightarrow 0$
. Especially for
![]() $A=F^{\prime }$
, we obtain
$A=F^{\prime }$
, we obtain
![]() $\operatorname{Ext}^{2}(F^{\prime },F^{\prime })=0$
. This forces
$\operatorname{Ext}^{2}(F^{\prime },F^{\prime })=0$
. This forces
![]() $F^{\prime }=0$
, because
$F^{\prime }=0$
, because
![]() $F^{\prime }$
is filtered by
$F^{\prime }$
is filtered by
![]() ${\mathcal{O}}_{C_{1}},{\mathcal{O}}_{C_{2}}(-1),\ldots ,{\mathcal{O}}_{C_{t}}(-1)$
, and for any smooth, rational curve
${\mathcal{O}}_{C_{1}},{\mathcal{O}}_{C_{2}}(-1),\ldots ,{\mathcal{O}}_{C_{t}}(-1)$
, and for any smooth, rational curve
![]() $C\subset X$
with
$C\subset X$
with
![]() $C^{2}<0$
, we have
$C^{2}<0$
, we have
![]() $\text{ext}^{2}({\mathcal{O}}_{C},{\mathcal{O}}_{C})=h^{1}({\mathcal{O}}_{C}(C))=-C^{2}-1$
.◻
$\text{ext}^{2}({\mathcal{O}}_{C},{\mathcal{O}}_{C})=h^{1}({\mathcal{O}}_{C}(C))=-C^{2}-1$
.◻
3.1 Euler pairing and Cartan matrix
Put
![]() $b_{i}:=C_{i}^{2}+2\leqslant 0$
for the exceptional sequence
$b_{i}:=C_{i}^{2}+2\leqslant 0$
for the exceptional sequence
![]() ${\mathcal{E}}=({\mathcal{O}}(-C_{1}-\cdots -C_{t}),\ldots ,{\mathcal{O}}(-C_{1}),{\mathcal{O}})$
.
${\mathcal{E}}=({\mathcal{O}}(-C_{1}-\cdots -C_{t}),\ldots ,{\mathcal{O}}(-C_{1}),{\mathcal{O}})$
.
Lemma 3.2. The Cartan matrix of
![]() ${\mathcal{E}}$
is
${\mathcal{E}}$
is
 $$\begin{eqnarray}\left(\begin{array}{@{}cccccc@{}}1 & b_{t} & \ast & \cdots \, & \ast & \ast \\ 0 & 1 & b_{t-1} & & \ast & \ast \\ 0 & 0 & 1 & & \ast & \ast \\ \vdots & & & \ddots & & \vdots \\ 0 & 0 & 0 & & 1 & b_{1}\\ 0 & 0 & 0 & \cdots \, & 0 & 1\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cccccc@{}}1 & b_{t} & \ast & \cdots \, & \ast & \ast \\ 0 & 1 & b_{t-1} & & \ast & \ast \\ 0 & 0 & 1 & & \ast & \ast \\ \vdots & & & \ddots & & \vdots \\ 0 & 0 & 0 & & 1 & b_{1}\\ 0 & 0 & 0 & \cdots \, & 0 & 1\end{array}\right)\end{eqnarray}$$
with upper triangular
![]() $(i,j)$
-entry
$(i,j)$
-entry
![]() $c_{ij}:=b_{t-(i-1)}+b_{t-i}+\cdots +b_{t-(j-2)}$
. Its associated quadratic form is
$c_{ij}:=b_{t-(i-1)}+b_{t-i}+\cdots +b_{t-(j-2)}$
. Its associated quadratic form is
Proof. By definition of the Cartan matrix,
![]() $c_{ij}=\unicode[STIX]{x1D712}(E_{i-1},E_{j-1})$
; because the sequence starts with
$c_{ij}=\unicode[STIX]{x1D712}(E_{i-1},E_{j-1})$
; because the sequence starts with
![]() $E_{0}$
. The upper triangular shape of the matrix is clear, as
$E_{0}$
. The upper triangular shape of the matrix is clear, as
![]() ${\mathcal{E}}$
is an exceptional sequence. By construction,
${\mathcal{E}}$
is an exceptional sequence. By construction,
![]() $E_{i}={\mathcal{O}}(-C_{1}-\cdots -C_{t-i})$
, and for
$E_{i}={\mathcal{O}}(-C_{1}-\cdots -C_{t-i})$
, and for
![]() $i\leqslant j$
, put
$i\leqslant j$
, put
![]() $D_{ij}:=C_{t+2-j}+\cdots +C_{t+1-i}$
. We use the Riemann–Roch formula
$D_{ij}:=C_{t+2-j}+\cdots +C_{t+1-i}$
. We use the Riemann–Roch formula
![]() $-C.K_{X}=2+C^{2}$
for a rational curve
$-C.K_{X}=2+C^{2}$
for a rational curve
![]() $C$
in the following computation:
$C$
in the following computation:
 $$\begin{eqnarray}\displaystyle c_{ij} & = & \displaystyle \unicode[STIX]{x1D712}({\mathcal{O}}(-C_{1}-\cdots -C_{t-(i-1)},{\mathcal{O}}(-C_{1}-\cdots -C_{t-(j-1)}))=\unicode[STIX]{x1D712}({\mathcal{O}}(D_{ij}))\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}D_{ij}^{2}-\frac{1}{2}D_{ij}.K_{X}+\unicode[STIX]{x1D712}({\mathcal{O}})=\frac{1}{2}D_{ij}^{2}+\frac{1}{2}\mathop{\sum }_{l=t+2-j}^{t+1-i}(2+C_{l}^{2})+1\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{l=t+2-j}^{t+1-i}C_{l}^{2}+(j-i-1)+(j-i)+1=\mathop{\sum }_{l=t+2-j}^{t+1-i}b_{l}=\mathop{\sum }_{l=i}^{j-1}b_{-l+t+1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{ij} & = & \displaystyle \unicode[STIX]{x1D712}({\mathcal{O}}(-C_{1}-\cdots -C_{t-(i-1)},{\mathcal{O}}(-C_{1}-\cdots -C_{t-(j-1)}))=\unicode[STIX]{x1D712}({\mathcal{O}}(D_{ij}))\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2}D_{ij}^{2}-\frac{1}{2}D_{ij}.K_{X}+\unicode[STIX]{x1D712}({\mathcal{O}})=\frac{1}{2}D_{ij}^{2}+\frac{1}{2}\mathop{\sum }_{l=t+2-j}^{t+1-i}(2+C_{l}^{2})+1\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{l=t+2-j}^{t+1-i}C_{l}^{2}+(j-i-1)+(j-i)+1=\mathop{\sum }_{l=t+2-j}^{t+1-i}b_{l}=\mathop{\sum }_{l=i}^{j-1}b_{-l+t+1}.\nonumber\end{eqnarray}$$
The formula for the quadratic form follows immediately. ◻
Proposition 3.3. The Euler pairing is symmetric if and only if all
![]() $C_{i}^{2}=-2$
.
$C_{i}^{2}=-2$
.
The quadratic form is positive definite if and only if
![]() $C_{i}^{2}=-2$
for all
$C_{i}^{2}=-2$
for all
![]() $i$
, or if
$i$
, or if
![]() $C_{j}^{2}=-3$
for a single curve with
$C_{j}^{2}=-3$
for a single curve with
![]() $C_{i}^{2}=-2$
for the rest.
$C_{i}^{2}=-2$
for the rest.
Proof. The claim about symmetry of the Euler form follows at once from the Cartan matrix computation of Lemma 3.2. For the second statement, note that two
![]() $(-3)$
-curves lead to a Cartan minor
$(-3)$
-curves lead to a Cartan minor
 $$\begin{eqnarray}\left(\begin{array}{@{}rrr@{}}1 & -1 & -1\\ 0 & 1 & -1\\ 0 & 0 & 1\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}rrr@{}}1 & -1 & -1\\ 0 & 1 & -1\\ 0 & 0 & 1\end{array}\right)\end{eqnarray}$$
whose associated quadratic form is indefinite. A single
![]() $(-4)$
-curve gives rise to a Cartan minor
$(-4)$
-curve gives rise to a Cartan minor
![]() $\left(\!\begin{smallmatrix}1 & -2\\ 0 & 1\end{smallmatrix}\!\right)$
whose quadratic form is negative.◻
$\left(\!\begin{smallmatrix}1 & -2\\ 0 & 1\end{smallmatrix}\!\right)$
whose quadratic form is negative.◻
3.2 Quivers
We show the quivers describing
![]() ${\mathcal{E}}$
and
${\mathcal{E}}$
and
![]() $\unicode[STIX]{x1D6EC}$
in the case of three curves with
$\unicode[STIX]{x1D6EC}$
in the case of three curves with
![]() $C_{i}^{2}=-2$
. The Ext quiver of the exceptional sequence
$C_{i}^{2}=-2$
. The Ext quiver of the exceptional sequence
![]() ${\mathcal{E}}=(E_{0},\ldots ,E_{3})=({\mathcal{O}}(-C_{1}-\cdots -C_{3}),\ldots ,{\mathcal{O}}(-C_{1}),{\mathcal{O}})$
is
${\mathcal{E}}=(E_{0},\ldots ,E_{3})=({\mathcal{O}}(-C_{1}-\cdots -C_{3}),\ldots ,{\mathcal{O}}(-C_{1}),{\mathcal{O}})$
is
Straight arrows indicate homomorphisms up to scalars, and dashed arrows 1-extensions. Reducible morphisms (composites) are not shown.
The iterated universal extension of
![]() ${\mathcal{E}}$
is
${\mathcal{E}}$
is
 $$\begin{eqnarray}T=T_{0}\oplus T_{1}\oplus T_{2}\oplus T_{3}={\mathcal{O}}\oplus \left(\begin{array}{@{}c@{}}{\mathcal{O}}(-C_{1})\\ {\mathcal{O}}\end{array}\right)\oplus \cdots \oplus \left(\begin{array}{@{}c@{}}{\mathcal{O}}(-C_{3}-C_{2}-C_{1})\\ {\mathcal{O}}(-C_{2}-C_{1})\\ {\mathcal{O}}(-C_{1})\\ {\mathcal{O}}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}T=T_{0}\oplus T_{1}\oplus T_{2}\oplus T_{3}={\mathcal{O}}\oplus \left(\begin{array}{@{}c@{}}{\mathcal{O}}(-C_{1})\\ {\mathcal{O}}\end{array}\right)\oplus \cdots \oplus \left(\begin{array}{@{}c@{}}{\mathcal{O}}(-C_{3}-C_{2}-C_{1})\\ {\mathcal{O}}(-C_{2}-C_{1})\\ {\mathcal{O}}(-C_{1})\\ {\mathcal{O}}\end{array}\right).\end{eqnarray}$$
Its endomorphism algebra
![]() $\unicode[STIX]{x1D6EC}=\operatorname{End}(T)$
is a finite-dimensional algebra. In the exact tilting equivalence,
$\unicode[STIX]{x1D6EC}=\operatorname{End}(T)$
is a finite-dimensional algebra. In the exact tilting equivalence,
![]() $\operatorname{Hom}(T,-):\text{Coh}_{{\mathcal{E}}}(X)\stackrel{{\sim}}{\longrightarrow }\text{mod}\text{-}\unicode[STIX]{x1D6EC}$
, the target category consists of right
$\operatorname{Hom}(T,-):\text{Coh}_{{\mathcal{E}}}(X)\stackrel{{\sim}}{\longrightarrow }\text{mod}\text{-}\unicode[STIX]{x1D6EC}$
, the target category consists of right
![]() $\unicode[STIX]{x1D6EC}$
-modules because
$\unicode[STIX]{x1D6EC}$
-modules because
![]() $T$
acts by precomposing on morphisms
$T$
acts by precomposing on morphisms
![]() $T\rightarrow A$
.
$T\rightarrow A$
.
Under tilting, the indecomposable summands
![]() $T_{i}$
become projective modules: writing
$T_{i}$
become projective modules: writing
![]() $P(i):=\operatorname{Hom}(T,T_{i})$
, we have
$P(i):=\operatorname{Hom}(T,T_{i})$
, we have
![]() $\unicode[STIX]{x1D6EC}=P(0)\oplus \cdots \oplus P(3)$
by construction, so that each
$\unicode[STIX]{x1D6EC}=P(0)\oplus \cdots \oplus P(3)$
by construction, so that each
![]() $P(i)$
is a direct summand of the free module.
$P(i)$
is a direct summand of the free module.
We study maps between these projective modules: first, there are injections
![]() $\unicode[STIX]{x1D6FC}_{i}:P(i){\hookrightarrow}P(i+1)$
for
$\unicode[STIX]{x1D6FC}_{i}:P(i){\hookrightarrow}P(i+1)$
for
![]() $i=0,1,2$
; these maps are part of the defining extensions. Second, there are morphisms in the other direction
$i=0,1,2$
; these maps are part of the defining extensions. Second, there are morphisms in the other direction
![]() $\unicode[STIX]{x1D6FD}_{i}:P(i+1)\rightarrow P(i)$
for
$\unicode[STIX]{x1D6FD}_{i}:P(i+1)\rightarrow P(i)$
for
![]() $i=0,1,2$
. For example
$i=0,1,2$
. For example
![]() $P(1)=\binom{{\mathcal{O}}(-C_{1})}{{\mathcal{O}}}{\twoheadrightarrow}{\mathcal{O}}(-C_{1}){\hookrightarrow}{\mathcal{O}}=P(0)$
. All other morphisms are linear combinations of compositions of these maps.
$P(1)=\binom{{\mathcal{O}}(-C_{1})}{{\mathcal{O}}}{\twoheadrightarrow}{\mathcal{O}}(-C_{1}){\hookrightarrow}{\mathcal{O}}=P(0)$
. All other morphisms are linear combinations of compositions of these maps.
Now
![]() $0=\unicode[STIX]{x1D6FD}_{0}\unicode[STIX]{x1D6FC}_{0}\in \operatorname{End}(P(0))$
, whereas
$0=\unicode[STIX]{x1D6FD}_{0}\unicode[STIX]{x1D6FC}_{0}\in \operatorname{End}(P(0))$
, whereas
![]() $\unicode[STIX]{x1D6FC}_{0}\unicode[STIX]{x1D6FD}_{0}=\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FC}_{1}\in \operatorname{End}(P(1))$
and
$\unicode[STIX]{x1D6FC}_{0}\unicode[STIX]{x1D6FD}_{0}=\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FC}_{1}\in \operatorname{End}(P(1))$
and
![]() $\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FD}_{1}=\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FC}_{2}\in \operatorname{End}(P(2))$
. There is no relation for
$\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FD}_{1}=\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FC}_{2}\in \operatorname{End}(P(2))$
. There is no relation for
![]() $\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}\in \operatorname{End}(P(3))$
.
$\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{2}\in \operatorname{End}(P(3))$
.
We follow common abuse of notation and drop the subscripts for the
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
arrows. Then the quiver of
$\unicode[STIX]{x1D6FD}$
arrows. Then the quiver of
![]() $\unicode[STIX]{x1D6EC}$
looks like
$\unicode[STIX]{x1D6EC}$
looks like
with a zero relation
![]() $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}=0$
at
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}=0$
at
![]() $P(0)$
, commutativity relations
$P(0)$
, commutativity relations
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}$
at intermediate vertices
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}$
at intermediate vertices
![]() $P(1),P(2)$
and no relation at
$P(1),P(2)$
and no relation at
![]() $P(3)$
.
$P(3)$
.
The algebra
![]() $\unicode[STIX]{x1D6EC}$
can now also be described as the path algebra of this quiver modulo the ideal generated by the specified relations, as in the textbooks on representations of finite-dimensional algebras [Reference Assem, Simson and Skowroński1, Reference Auslander, Reiten and Smalø2].
$\unicode[STIX]{x1D6EC}$
can now also be described as the path algebra of this quiver modulo the ideal generated by the specified relations, as in the textbooks on representations of finite-dimensional algebras [Reference Assem, Simson and Skowroński1, Reference Auslander, Reiten and Smalø2].
For arbitrary negative intersection numbers
![]() $C_{i}^{2}$
, the quivers with relations are given in [Reference Kalck and Karmazyn10, Section 5].
$C_{i}^{2}$
, the quivers with relations are given in [Reference Kalck and Karmazyn10, Section 5].
Acknowledgments
A lot of this research has been conducted at Mathematisches Forschungsinstitut Oberwolfach during a Research-in-pairs stay for which we are very grateful. We thank Martin Kalck for his interest in this work and valuable input, and we thank the anonymous referee.