No CrossRef data available.
Article contents
The Gradient Superconvergence of Bilinear Finite Volume Element for Elliptic Problems
Part of:
Partial differential equations, initial value and time-dependent initial-boundary value problems
Partial differential equations, boundary value problems
Published online by Cambridge University Press: 17 November 2016
Abstract
We study the gradient superconvergence of bilinear finite volume element (FVE) solving the elliptic problems. First, a superclose weak estimate is established for the bilinear form of the FVE method. Then, we prove that the gradient approximation of the FVE solution has the superconvergence property:
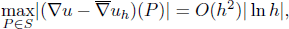
where 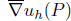 denotes the average gradient on elements containing point P and S is the set of optimal stress points composed of the mesh points, the midpoints of edges and the centers of elements.
denotes the average gradient on elements containing point P and S is the set of optimal stress points composed of the mesh points, the midpoints of edges and the centers of elements.
Information
- Type
- Research Article
- Information
- Numerical Mathematics: Theory, Methods and Applications , Volume 9 , Issue 4 , November 2016 , pp. 579 - 594
- Copyright
- Copyright © Global-Science Press 2016
References
[1]
Cai, Z.Q., On the finite volume element method, Numer. Math., 58 (1991), pp. 713–735.Google Scholar
[2]
Chen, Z.Y., L2 estimate of linear element generalized difference schemes, Acta. Sci. Nat. Univ. Sunyatseni, 33 (1994), pp. 22–28.Google Scholar
[3]
Chen, Z.Y., Superconvergence of generalized difference methods for elliptic boundary value problem, Numer. Math. A J. of Chinese Univ.(English Ser), 3 (1994), pp. 163–171.Google Scholar
[4]
Chen, Z.Y., Li, R.H. and Zhou, A.H., A note on the optimal L2-estimate of the finite volume element method, Adv. Comput. Math., 16 (2002), pp. 291–303.Google Scholar
[5]
Chen, L., A new class of high order finite volume element methods for second order elliptic equations, SIAM J. Numer. Anal., 47 (2010), pp. 4021–4023.Google Scholar
[6]
Chou, S.H. and Li, Q., Error estimates in L2, H1, L∞ in covolume methods for elliptic and parabolic problem: a unified approach, Math. Comp., 69 (2000), pp. 103–120.Google Scholar
[7]
Chou, S.H. and Ye, X., Superconvergence of finite volume methods for the second order elliptic problem, Comput. Methods Appl. Mech. Engrg., 196 (2007), pp. 3706–3712.Google Scholar
[8]
Ewing, R.E., Lin, T. and Lin, Y.P., On the accuracy of the finite volume element method based on piecewise linear polynomials
SIAM J. Numer. Anal., 39 (2002), pp. 1865–1888.CrossRefGoogle Scholar
[9]
Lazarov, R., Michev, I. and Vassilevski, P., Finite volumemethods for convection-diffusion problems, SIAM J. Numer. Anal., 33 (1996), pp. 31–55.Google Scholar
[10]
Li, R.H., Chen, Z.Y. and Wu, W., Generalized difference methods for differential equations: numerical analysis of finite volume methods, Marcel, New York, 2000.Google Scholar
[11]
Lin, Q. and Zhu, Q.D., The preprocessing and postprocessing for the finite element methods, Shanghai Sci & Tech Publishing, Shanghai, 1994.Google Scholar
[12]
Lv, J.L. and Li, Y.H., L2 error estimates and superconvergence of the finite volume element methods on quadrilateral meshes, Adv. Comput. Math., 37 (2012), pp. 393–416.CrossRefGoogle Scholar
[13]
Süli, E., Convergence of finite volume schemes for poission's equation on nonuniform meshes, SIAM J. Numer. Anal., 28 (1991), pp. 1419–1430.Google Scholar
[14]
Wu, H.J. and Li, R.H., Error estimate for finite volume element methods for general second order elliptic problem, Numer. Meth. PDEs., 19 (2003), pp. 693–708.Google Scholar
[15]
Xu, J.C. and Zou, Q.S., Analysis of linear and quadratic simplical finite volume methods for elliptic equations, Numer. Math., 111 (2009), pp. 469–492.Google Scholar
[16]
Zhang, L. and Li, L.K., On superconvergence of isopareametric bilinear finite elements, Comm. Numer. Meth. Enrg., 12 (1996), pp. 849–862.3.0.CO;2-N>CrossRefGoogle Scholar
[17]
Zhang, T., Lin, Y.P. and Tait, R.J., On the finite volume element version of Ritz-Volterra projection and applications to related equations, J. Comp. Math., 20 (2002), pp. 491–504.Google Scholar
[18]
Zhang, T. and Sheng, Y., Superconvergence and Gradient Recovery for a Finite Volume Element Method for Solving Convection-Diffusion Equations, Numer. Meth. PDEs., 30 (2014), pp. 1152–1168.Google Scholar
[19]
Zhang, T., Finite element methods for partial differential-integral equations, Science Press, Beijing, 2009.Google Scholar
[20]
Zhang, Z.M. and Zou, Q.S., Some recent advances on vertex centered finite volume element methods for elliptic equations, Sci. China Mathematics, 56 (2013), pp. 2507–2522.Google Scholar
[21]
Zhu, Q.D. and Lin, Q., The superconvergence theory of finite elements, Hunan Science and Technology Publishing House, Changsha, 1989.Google Scholar

