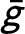1 Introduction
We introduce a priority mechanism that matches agents to locations in instances where a planner/designer (hereafter, planner) can set a minimum acceptable threshold on her own measure of aggregate welfare. The design of our mechanism is motivated by the assignment of refugee families to host country locations. In this context, refugee families have preferences over locations, and host governments would like to conduct the assignment to take account of these preferences, but these governments would also like to make sure that their own measure of social welfare is not compromised so much so that it falls below a prespecified threshold. In the refugee assignment problem, host country governments may consider their measure of social welfare to be an index of predicted integration success as measured by, for example, employment or earnings. In other applications such as student assignment to schools, this measure of welfare could be the average GPA of students, or their performance in standardized tests—measures that are typically of concern to school boards.
Our mechanism is a priority mechanism but differs from the canonical version (e.g., Satterthwaite and Sonnenschein Reference Satterthwaite and Sonnenschein1981) in the following respects. After preferences are elicited from the agents and the agents are lined up in a random order, each successive agent is assigned to their highest-ranked location provided that assigning them to that location meets two conditions: (i) there is an available seat at that location and (ii) there is a way to complete the assignment of the remaining agents that respects the planner’s threshold. We assume that agents can rank locations strictly, except possibly their worst-ranked locations. If there is no location that an agent can rank strictly that meets the two criteria above, then the agent is put in a “holding set” and will be assigned to one of their worst-ranked locations (over which they are indifferent) at the end of the process. At this point, all agents in the holding set are assigned to locations to maximize the planner’s welfare measure, and the assignment is complete.
Outcome-based matching was introduced in the context of refugee assignment to host country resettlement locations by Bansak et al. (Reference Bansak2018).Footnote 1 The idea in outcome-based matching is to assign agents to locations so as to maximize a social planner’s welfare measure, for example, the refugee’s expected employment success. Data-driven algorithms train supervised learners on historical data to discover synergies between places and types of refugees. The learned models are then used for newly arriving refugees to predict their expected integration success and optimally match them to locations where they have the highest probability of success subject to capacity and other constraints. Outcome-based matching is appealing because it harnesses historical data to maximize expected integration success and does not require collecting data on refugee preferences. Indeed, the outcome-based refugee matching methods as proposed by Bansak et al. (Reference Bansak2018) have already been implemented in the real world by research teams in collaboration with resettlement organizations. One implementation was conducted by the Swiss State Secretariat of Migration in collaboration with the Bansak et al. (Reference Bansak2018) research team. Another implementation of the methods proposed by Bansak et al. (Reference Bansak2018) was conducted by Trapp et al. (Reference Trapp, Teytelboym, Martinello, Andersson and Ahani2018) with HIAS, a resettlement agency in the United States. However, a pure outcome-based approach does not take preferences into account and does not utilize private information that refugees may possess regarding which location would work best for them.
Our mechanism addresses this limitation by assigning agents based on their preferences, to an extent that is acceptable to the planner. It draws on the strengths of both the pure preference-based approach and the data-driven outcome-based approach, allowing the planner to harness the power of data-driven assignment to ensure some minimum level of welfare while taking into account the preferences of the agents. The mechanism achieves this by integrating the data-driven matching algorithm of Bansak et al. (Reference Bansak2018) into a priority mechanism for preference-based matching.
Our mechanism has several desirable properties. First, it strikes a compromise between the need of the planner to ensure a minimum level for their measure of average welfare and the appeal of incorporating agents’ preferences.Footnote 2 Second, despite the added complexity of accounting for the planner’s constraint, our mechanism inherits the desirable properties of priority mechanisms. It remains strategy-proof and hence is immune to strategic manipulation through false reporting of preferences. It is constrained Pareto-efficient in that it generates an assignment that is not Pareto dominated by another assignment that also satisfies the planner’s constraint. It also allows agents to express preferences without the requirement that they strictly rank all locations. This flexibility is important, especially in the refugee assignment context, since there may be a large degree of heterogeneity as to whether refugees have distinct preferences over all locations. Finally, the mechanism is both computationally and administratively feasible. It can be implemented by the planner with only minor adjustments to existing methods. It only requires the additional step of eliciting agents’ preferences.
We provide two applications of our mechanism using data from two distinct settings. In the first, we illustrate how our mechanism could be used to assign refugees admitted into the United States to American cities, taking the planner’s welfare measure to the be expected level of employment of a member of the refugee household within 90 days of resettlement. The importance of matching refugees to host country locations as a tool to improve integration success is discussed in Mousa (Reference Mousa2018), and there have been many proposals for how host countries may approach the matching problem (e.g., Moraga and Rapoport Reference Moraga and Rapoport2014; Fernández-Huertas Moraga and Rapoport Reference Fernández-Huertas Moraga and Rapoport2015; Delacrétaz, Kominers, and Teytelboym Reference Delacrétaz, Kominers and Teytelboym2016; Andersson and Ehlers Reference Andersson and Ehlers2016; Bansak et al. Reference Bansak2018; Roth 2018; Trapp et al. Reference Trapp, Teytelboym, Martinello, Andersson and Ahani2018; Gölz and Procaccia Reference Gölz and Procaccia2019; Bansak Reference Bansak2020). The idea of refugee matching is to select locations that are likely to be a good fit for a given refugee to thrive, and extant research has shown that the place of initial settlement has a profound impact on the long-term integration success of refugees (Åslund and Rooth Reference Åslund and Rooth2007; Damm Reference Damm2014; Bansak et al. Reference Bansak2018; Martén, Hainmueller, and Hangartner Reference Martén, Hainmueller and Hangartner2019).
In practice, however, the assignment of refugees in most countries is usually determined by simple capacity constraints and/or proportional distribution keys. Governments want to ensure that refugees become self-sufficient and are typically reluctant to let them freely choose where to settle due to concerns that this could result in a highly uneven regional distribution and the creation of ethnic enclaves. That said, a few governments have started to appreciate the value of eliciting the refugee families’ own preferences over locations.Footnote 3 Recognizing this value, the Dutch government, for example, has started collecting unstructured information on the location preferences of refugee families as part of their interviews. However, there currently exist no systematic data on refugee preferences, including in the United States. As a result, for our evaluation, we impute refugee preferences based on secondary migration data.
In our second application, we demonstrate how our mechanism could be applied outside of refugee matching. In this application, we apply the mechanism to the problem of matching kindergarteners to schools in Tennessee, taking the planner’s welfare measure to be the sum of their reading, math, and listening scaled scores on the Stanford Achievement Test (SAT) for the Kindergarten level. School choice is a canonical application in the matching literature (see, e.g., Abdulkadiroğlu and Sönmez Reference Abdulkadiroğlu and Sönmez2003; Abdulkadiroğlu, Pathak, and Roth Reference Abdulkadiroğlu, Pathak and Roth2009; Abdulkadiroglu and Sönmez Reference Abdulkadiroglu and Sönmez2013; Pathak Reference Pathak2011, Reference Pathak, Honoré, Pakes, Piazzesi and Samuelson2017; Ehlers et al. Reference Ehlers, Hafalir, Yenmez and Yildirim2014) and thus serves as a useful second context in which to illustrate our mechanism.
Our paper contributes to the recent market design literature that takes into account a planner’s constraints (Echenique and Yenmez Reference Echenique and Yenmez2015; Kamada and Kojima Reference Kamada and Kojima2015; Dur et al. Reference Dur, Kominers, Pathak and Sönmez2018). Two papers along these lines are particularly related. The first (Narita Reference Narita2019) looks at the problem of assigning subjects to treatments in a randomized control trial to maximize the welfare of the subjects subject to the constraint that the researcher gleans a certain level of scientific information from running the trial. The second (Delacrétaz et al. Reference Delacrétaz, Kominers and Teytelboym2016) considers several variants of the top trading cycle (TTC) mechanism, first allowing for multidimensional constraints and then allowing for the agents to have a starting endowment. Since these mechanisms do not respect both strategy-proofness and Pareto efficiency, they relax the efficiency requirement and impose the condition that there be no sequence of swaps that generate a Pareto-improving assignment. Our paper differs from this prior work in that we incorporate preferences into the assignment problem while fixing a minimum expected outcome threshold.
Although our mechanism is both constrained efficient and strategy-proof, we also investigate how well we can do on a second metric of welfare, namely the percent of agents that receive one of their highly (e.g., top-three) ranked locations. When we take a sample of rerandomizations of the priority order of agents, we find that there may be substantial potential gains to be made on this welfare metric.Footnote 4 We then suggest two ways of potentially capturing these gains without violating the requirement that the mechanism be strategy-proof.Footnote 5 The first is to use historical data to predict the preferences of the agents based on their observable traits, then fix the ordering that does best on this metric under the predicted preferences, and finally, elicit the agents’ actual preferences and assign them according to this ordering. The second is to fix the ordering of agents so that an agent with a lower variance in outcome scores across locations is served before one with a higher variance.
A final contribution of our study is to open a closer dialogue between political methodology and the study of market design. Political methodology has historically thrived on interdisciplinary engagement with methods developed in related disciplines, such as statistics, econometrics, psychometrics, and computer science. Yet, for some reason, it has largely neglected to engage with the foundational work that has developed in economics on the study of market and mechanism design.Footnote 6 This is an unfortunate omission, because market and mechanism design is arguably at the core of many issues that are highly relevant to political science. Fundamentally, market design is about engineering institutions to ensure that they generate desired outcomes, such as an efficient or equitable distribution of opportunities or resources. As economist Alvin Roth recently put it, market design is about “Who gets what—and why” (Roth 2015). This phrase resembles one of the canonical definitions of politics as “Who gets what, when, and how” by Harold Lasswell (Lasswell Reference Lasswell1936). Institutional mechanisms that allocate opportunities and resources are a central feature of modern democracies, and algorithms are increasingly used for public policy in a wide variety of domains. We hope that our study can help pave a path for political methodology to begin to contribute to these important developments given its unique blend of expertise.
2 The Mechanism
2.1 Preliminaries
There are n agents (refugee families/school children) randomly labeled
![]() $1,...,n$
, each of which has to be assigned to a location (host country city or town/school). Let L denote the finite set of locations. Each location
$1,...,n$
, each of which has to be assigned to a location (host country city or town/school). Let L denote the finite set of locations. Each location
![]() $l \in L$
has a capacity
$l \in L$
has a capacity
![]() $q_l \geq 1$
as to how many agents it can accommodate. We assume that
$q_l \geq 1$
as to how many agents it can accommodate. We assume that
![]() $n \leq \sum _l q_l$
so that it is feasible to assign all agents. For each agent i, let
$n \leq \sum _l q_l$
so that it is feasible to assign all agents. For each agent i, let
![]() $g_i(l)$
be a measure of success at location l (employment probability/test scores) when assigned to that location. In practice, this measure may need to be estimated, in which case it represents an agent’s success at location l in expectation. This measure may be accounted for in the agent’s preferences but is the key consideration for a social planner. We refer to
$g_i(l)$
be a measure of success at location l (employment probability/test scores) when assigned to that location. In practice, this measure may need to be estimated, in which case it represents an agent’s success at location l in expectation. This measure may be accounted for in the agent’s preferences but is the key consideration for a social planner. We refer to
![]() $g_i(l)$
as the planner’s outcome score for agent i at location l.
$g_i(l)$
as the planner’s outcome score for agent i at location l.
Each agent i has a complete and transitive preference ordering
![]() $\succsim _i$
over the set of locations.Footnote
7
Indifference and the strict preference relations are denoted by
$\succsim _i$
over the set of locations.Footnote
7
Indifference and the strict preference relations are denoted by
![]() $\sim _i$
and
$\sim _i$
and
![]() $\succ _i$
, respectively, and
$\succ _i$
, respectively, and
![]() $\succsim = {(\succsim _1,...,\succsim _n)}$
denotes the vector of preferences.
$\succsim = {(\succsim _1,...,\succsim _n)}$
denotes the vector of preferences.
We make the assumption on agents’ preferences that the only indifferences are over the worst-ranked locations. That is, apart from possibly having ties among a set of locations that an agent deems to be the worst, each agent has a strict preference over all of the other locations. Formally, for all agents i, if
![]() $l \sim _i l'$
for some
$l \sim _i l'$
for some
![]() $l' \neq l$
, there is no
$l' \neq l$
, there is no
![]() $l''$
such that
$l''$
such that
![]() $l \succ _i l''$
. This still allows for an agent to be indifferent over all locations. This assumption is motivated by our application to refugee assignment: refugee families often do not have full information on all possible locations, but they may have (strict) preferences over a limited set of top choices.Footnote
8
$l \succ _i l''$
. This still allows for an agent to be indifferent over all locations. This assumption is motivated by our application to refugee assignment: refugee families often do not have full information on all possible locations, but they may have (strict) preferences over a limited set of top choices.Footnote
8
Define the set
![]() $S_i = L \backslash \{l \in L : \exists l' \sim _i l\}$
, which are all of the locations except any that agent i is indifferent over. Agent i has a strict preference across all locations in
$S_i = L \backslash \{l \in L : \exists l' \sim _i l\}$
, which are all of the locations except any that agent i is indifferent over. Agent i has a strict preference across all locations in
![]() $S_i$
, and if any location is left out of
$S_i$
, and if any location is left out of
![]() $S_i$
, then it must have been ranked worst.
$S_i$
, then it must have been ranked worst.
A matching
![]() $\mu $
maps the set of agents to locations. A matching
$\mu $
maps the set of agents to locations. A matching
![]() $\mu $
is
$\mu $
is
-
1. feasible if it satisfies the capacity constraints:
 $|\mu ^{-1} (l)| \leq q_l, \forall l$
;
$|\mu ^{-1} (l)| \leq q_l, \forall l$
; -
2.
 $\bar g$
-acceptable if the average outcome score is not lower than
$\bar g$
-acceptable if the average outcome score is not lower than
 $\bar g$
:
$\bar g$
:
 $\frac {1}{n} \sum _i g_{i} (\mu (i)) \geq \bar g$
.
$\frac {1}{n} \sum _i g_{i} (\mu (i)) \geq \bar g$
.
![]() $\bar g$
-acceptability reflects the idea that the planner wants the average outcome score not to fall below a specified threshold
$\bar g$
-acceptability reflects the idea that the planner wants the average outcome score not to fall below a specified threshold
![]() $\bar g$
. The planner wants to ensure that the allocation is such that agents have some minimum level of expected outcomes (e.g., a minimum expected employment rate/GPA or test score).
$\bar g$
. The planner wants to ensure that the allocation is such that agents have some minimum level of expected outcomes (e.g., a minimum expected employment rate/GPA or test score).
Note that not all values of
![]() $\bar g$
can produce a feasible matching. Let
$\bar g$
can produce a feasible matching. Let
![]() $\bar g^{\text {max}}$
denote the highest possible average outcome score that can be generated by a feasible matching
$\bar g^{\text {max}}$
denote the highest possible average outcome score that can be generated by a feasible matching
 $$ \begin{align} \bar g^{\text{max}} := \max_{\mu} \frac{1}{n} \sum_i g_i ( \mu(i)) \text{ subject to } |\mu^{-1} (l)| \leq q_l, \forall l. \end{align} $$
$$ \begin{align} \bar g^{\text{max}} := \max_{\mu} \frac{1}{n} \sum_i g_i ( \mu(i)) \text{ subject to } |\mu^{-1} (l)| \leq q_l, \forall l. \end{align} $$
Feasible
![]() $\bar g$
-acceptable matchings exist only for
$\bar g$
-acceptable matchings exist only for
![]() $\bar g \leq \bar g^{\text {max}}$
.
$\bar g \leq \bar g^{\text {max}}$
.
2.2 The Assignment Procedure
Given a value of
![]() $\bar g \leq \bar g^{\max }$
, the algorithm starts with agent 1 and works down to agent n in a sequence of n steps before completing in either the nth or an additional
$\bar g \leq \bar g^{\max }$
, the algorithm starts with agent 1 and works down to agent n in a sequence of n steps before completing in either the nth or an additional
![]() $(n+1)$
th step. At Step
$(n+1)$
th step. At Step
![]() $i \leq n$
, agent i is either assigned to a location or put on hold by being added to a set of temporarily unassigned agents that will all get assigned simultaneously at Step
$i \leq n$
, agent i is either assigned to a location or put on hold by being added to a set of temporarily unassigned agents that will all get assigned simultaneously at Step
![]() $n+1$
. At each Step i, let
$n+1$
. At each Step i, let
![]() $N_i$
denote the set of agents
$N_i$
denote the set of agents
![]() $j < i$
that have been put on hold.
$j < i$
that have been put on hold.
![]() $N_1 = \emptyset $
, since at the start of the algorithm, no agent is on hold.
$N_1 = \emptyset $
, since at the start of the algorithm, no agent is on hold.
If agent
![]() $j < i$
was assigned a location prior to Step i, then let
$j < i$
was assigned a location prior to Step i, then let
![]() $\alpha _i (j)$
denote the location and
$\alpha _i (j)$
denote the location and
![]() $(j, \alpha _i(j))$
the assignment, viewing
$(j, \alpha _i(j))$
the assignment, viewing
![]() $\alpha _i$
as a function. Refer to this function as the completed assignment at Step i. Note that
$\alpha _i$
as a function. Refer to this function as the completed assignment at Step i. Note that
![]() $\alpha _1 = \emptyset $
, so the completed assignment at Step 1 is trivial. A remaining assignment
$\alpha _1 = \emptyset $
, so the completed assignment at Step 1 is trivial. A remaining assignment
![]() $\beta _i$
at Step i is a mapping of the unassigned agents
$\beta _i$
at Step i is a mapping of the unassigned agents
![]() $\{i,...,n\} \cup N_i$
to locations such that
$\{i,...,n\} \cup N_i$
to locations such that
 $$ \begin{align*} \mu_{(\alpha_i, \beta_i)} (j) := \left\{\begin{array}{ll} \alpha_i(j) &\quad \text{if } j < i\\ \beta_i(j) &\quad \text{if } j \in \{i,...,n\} \cup N_i \end{array}\right. \end{align*} $$
$$ \begin{align*} \mu_{(\alpha_i, \beta_i)} (j) := \left\{\begin{array}{ll} \alpha_i(j) &\quad \text{if } j < i\\ \beta_i(j) &\quad \text{if } j \in \{i,...,n\} \cup N_i \end{array}\right. \end{align*} $$
is a matching. We refer to
![]() $\mu _{(\alpha _i, \beta _i)}$
as the matching associated with the pair of completed and remaining assignments
$\mu _{(\alpha _i, \beta _i)}$
as the matching associated with the pair of completed and remaining assignments
![]() $(\alpha _i, \beta _i)$
. The existence of these matchings will be guaranteed recursively by the algorithm.
$(\alpha _i, \beta _i)$
. The existence of these matchings will be guaranteed recursively by the algorithm.
At each Step
![]() $i \leq n$
, given
$i \leq n$
, given
![]() $\alpha _i$
, define the set
$\alpha _i$
, define the set
 $$ \begin{align*} L^{\bar g}_i (\alpha_i) = \{ l \in L : \exists \beta_i \text{ s.t. } l = \beta_i (i) \text{ and } \mu_{(\alpha_i, \beta_i)} \text{ is a feasible } \bar g\text{-acceptable matching}\}. \end{align*} $$
$$ \begin{align*} L^{\bar g}_i (\alpha_i) = \{ l \in L : \exists \beta_i \text{ s.t. } l = \beta_i (i) \text{ and } \mu_{(\alpha_i, \beta_i)} \text{ is a feasible } \bar g\text{-acceptable matching}\}. \end{align*} $$
This is the set of locations that are not at full capacity and for which there is a way to finish assigning all unassigned agents so as to create a feasible
![]() $\bar g$
-acceptable matching.
$\bar g$
-acceptable matching.
Let
![]() $q^i_l$
be the remaining capacity of location l after any agents ahead of i (i.e.,
$q^i_l$
be the remaining capacity of location l after any agents ahead of i (i.e.,
![]() $j < i$
) have been assigned in the previous
$j < i$
) have been assigned in the previous
![]() $i-1$
steps. At the start, we have
$i-1$
steps. At the start, we have
 $q^1_l = q_l$
for all l. It will also be convenient to define the following problems: for all Steps
$q^1_l = q_l$
for all l. It will also be convenient to define the following problems: for all Steps
![]() $i=1,...,n+1$
, and given a vector
$i=1,...,n+1$
, and given a vector
 $q^i := (q^i_l)_{l \in L}$
,
$q^i := (q^i_l)_{l \in L}$
,
 $$ \begin{align} G_i (q^i) := \max_{\beta_i} \sum_{j \in \{i,...,n\} \cup N_i} g_j (\beta_i (j)) \text{ subject to } |\beta_i^{-1} (l) | \leq q^i_l, \forall l, \end{align} $$
$$ \begin{align} G_i (q^i) := \max_{\beta_i} \sum_{j \in \{i,...,n\} \cup N_i} g_j (\beta_i (j)) \text{ subject to } |\beta_i^{-1} (l) | \leq q^i_l, \forall l, \end{align} $$
with the convention that
![]() $\{i,...,n\} := \emptyset $
if
$\{i,...,n\} := \emptyset $
if
![]() $i = n+1$
. At each Step i, the problem in (2) finds the remaining assignment that maximizes the total outcome score subject to the updated capacity constraints at Step i. The solution to this problem at each step determines whether the associated matching is
$i = n+1$
. At each Step i, the problem in (2) finds the remaining assignment that maximizes the total outcome score subject to the updated capacity constraints at Step i. The solution to this problem at each step determines whether the associated matching is
![]() $\bar g$
-acceptable. In fact, to verify whether or not a location l belongs in
$\bar g$
-acceptable. In fact, to verify whether or not a location l belongs in
 $L^{\bar g}_i(\alpha _i)$
, we must first check whether the highest possible value of the average outcome score that can be achieved under the remaining assignment is at least
$L^{\bar g}_i(\alpha _i)$
, we must first check whether the highest possible value of the average outcome score that can be achieved under the remaining assignment is at least
![]() $\bar g$
; i.e., whether
$\bar g$
; i.e., whether
 $$ \begin{align*} \bar g_i(l) := \frac{1}{n} \left( G_{i+1}(q^{i+1}) + g_i (l) + \sum_{j < i \text{ s.t.~}j \notin N_i} g_j (\alpha_i(j)) \right) \geq \bar g, \end{align*} $$
$$ \begin{align*} \bar g_i(l) := \frac{1}{n} \left( G_{i+1}(q^{i+1}) + g_i (l) + \sum_{j < i \text{ s.t.~}j \notin N_i} g_j (\alpha_i(j)) \right) \geq \bar g, \end{align*} $$
where
 $q^{i+1}_{l'} = q^i_{l'}$
for all
$q^{i+1}_{l'} = q^i_{l'}$
for all
![]() $l' \neq l$
and
$l' \neq l$
and
 $q^{i+1}_{l}= q^i_{l} -1$
. If indeed
$q^{i+1}_{l}= q^i_{l} -1$
. If indeed
![]() $\bar g_i(l) \geq \bar g$
and
$\bar g_i(l) \geq \bar g$
and
 $q^i_{l}> 0$
, then l belongs to
$q^i_{l}> 0$
, then l belongs to
 $L^{\bar g}_i (\alpha _i)$
; otherwise, it does not. Constructing
$L^{\bar g}_i (\alpha _i)$
; otherwise, it does not. Constructing
 $L^{\bar g}_i(\alpha _i)$
at each Step
$L^{\bar g}_i(\alpha _i)$
at each Step
![]() $i=1,...,n+1$
, therefore, requires solving the problems given in (2). In addition, to verify whether
$i=1,...,n+1$
, therefore, requires solving the problems given in (2). In addition, to verify whether
![]() $\bar g \leq \bar g^{\max }$
also requires solving one of these problems, since the problem in (1) equals
$\bar g \leq \bar g^{\max }$
also requires solving one of these problems, since the problem in (1) equals
![]() $G_1 (q^1)/n$
.
$G_1 (q^1)/n$
.
The steps of the algorithm are as follows.
-
Step 0. Verify that
 $\bar g \leq \bar g^{\max }$
and proceed only if it holds.
$\bar g \leq \bar g^{\max }$
and proceed only if it holds. -
Step i ≤ n. If
 $S_i \cap L^{\bar g}_i (\alpha _i)$
is empty (meaning that there is no location that agent i ranked strictly to which it could be assigned that would allow us also to find a remaining assignment that generates a feasible
$S_i \cap L^{\bar g}_i (\alpha _i)$
is empty (meaning that there is no location that agent i ranked strictly to which it could be assigned that would allow us also to find a remaining assignment that generates a feasible
 $\bar g$
-acceptable matching), then place agent i on hold. In this case, set and move on to Step
$\bar g$
-acceptable matching), then place agent i on hold. In this case, set and move on to Step $$ \begin{align*} N_{i+1} = N_i \cup \{i\}, \alpha_{i+1}= \alpha_{i}, q^{i+1}_l = q^i_l~\forall l \end{align*} $$
$$ \begin{align*} N_{i+1} = N_i \cup \{i\}, \alpha_{i+1}= \alpha_{i}, q^{i+1}_l = q^i_l~\forall l \end{align*} $$
 $i+1$
. Otherwise, if
$i+1$
. Otherwise, if
 $S_i \cap L^{\bar g}_i (\alpha _i)$
is nonempty, then it contains a unique best location from the perspective of agent i—i.e., a location
$S_i \cap L^{\bar g}_i (\alpha _i)$
is nonempty, then it contains a unique best location from the perspective of agent i—i.e., a location
 $l_i^*$
such that
$l_i^*$
such that
 $l_i^* \succ _i l$
for all
$l_i^* \succ _i l$
for all
 $l \in S_i \cap L^{\bar g}_i(\alpha _i)$
. This follows from the fact that i ranks the elements of
$l \in S_i \cap L^{\bar g}_i(\alpha _i)$
. This follows from the fact that i ranks the elements of
 $S_i$
strictly. Assign agent i to
$S_i$
strictly. Assign agent i to
 $l_i^*$
, and set If
$l_i^*$
, and set If $$ \begin{align*} N_{i+1} = N_i, \alpha_{i+1}= \alpha_{i} \cup \{(i,l_i^*)\}, q^{i+1}_{l_i^*} = q^i_{l_i^*}-1, \text{ and } q^{i+1}_l = q^i_l \forall l \neq l_i^*. \end{align*} $$
$$ \begin{align*} N_{i+1} = N_i, \alpha_{i+1}= \alpha_{i} \cup \{(i,l_i^*)\}, q^{i+1}_{l_i^*} = q^i_{l_i^*}-1, \text{ and } q^{i+1}_l = q^i_l \forall l \neq l_i^*. \end{align*} $$
 $i<n$
, then move to Step
$i<n$
, then move to Step
 $i+1$
. If
$i+1$
. If
 $i = n$
, then move to Step
$i = n$
, then move to Step
 $n+1$
only if an agent was ever put on hold (i.e.,
$n+1$
only if an agent was ever put on hold (i.e.,
 $N_{n+1} \neq \emptyset $
); otherwise, stop.
$N_{n+1} \neq \emptyset $
); otherwise, stop.
-
Step n + 1. At this stage, the only unassigned agents are those that were put on hold in
 $N_{n+1}$
. Here, choose any remaining assignment that maximizes the average outcome score given the completed assignment and the capacity constraints; that is, solve (2) for
$N_{n+1}$
. Here, choose any remaining assignment that maximizes the average outcome score given the completed assignment and the capacity constraints; that is, solve (2) for
 $i = n+1$
and stop.
$i = n+1$
and stop.
For any preference vector
![]() $\succsim $
satisfying our assumptions, our algorithm produces a matching, namely
$\succsim $
satisfying our assumptions, our algorithm produces a matching, namely
![]() $\mu _{(\alpha _s, \beta _s)}$
, where
$\mu _{(\alpha _s, \beta _s)}$
, where
![]() $s \in \{n, n+1\}$
was the step at which the algorithm stopped. The algorithm defines a mechanism
$s \in \{n, n+1\}$
was the step at which the algorithm stopped. The algorithm defines a mechanism
![]() $\varphi $
, which, given the other parameters of the model, is a mapping from preference vectors to feasible matchings. We refer to the mechanism as
$\varphi $
, which, given the other parameters of the model, is a mapping from preference vectors to feasible matchings. We refer to the mechanism as
![]() $\bar g$
-constrained priority, since it is a modification of the usual priority mechanism (Satterthwaite and Sonnenschein Reference Satterthwaite and Sonnenschein1981).
$\bar g$
-constrained priority, since it is a modification of the usual priority mechanism (Satterthwaite and Sonnenschein Reference Satterthwaite and Sonnenschein1981).
At each Step i, implementation of the mechanism involves iteratively solving the maximization problem in Equation 2 to verify that
![]() $\bar g$
-acceptability can still be met if agent i were assigned to each available location in order of preference, until such a location is found. This amounts to iteratively solving a standard linear sum assignment problem, for which various polynomial-time algorithms exist.Footnote
9
Under a worst-case scenario where every agent is put on hold after unsuccessfully considering all of its strictly ranked locations, this would require solving an equally sized maximization problem in Equation 2 a total of
$\bar g$
-acceptability can still be met if agent i were assigned to each available location in order of preference, until such a location is found. This amounts to iteratively solving a standard linear sum assignment problem, for which various polynomial-time algorithms exist.Footnote
9
Under a worst-case scenario where every agent is put on hold after unsuccessfully considering all of its strictly ranked locations, this would require solving an equally sized maximization problem in Equation 2 a total of
![]() $n (|L|-2)$
times.Footnote
10
$n (|L|-2)$
times.Footnote
10
2.3 Properties of the Mechanism
Let
![]() $\varphi (\succsim )$
denote the matching produced by the
$\varphi (\succsim )$
denote the matching produced by the
![]() $\bar g$
-constrained priority mechanism for any preference vector
$\bar g$
-constrained priority mechanism for any preference vector
![]() $\succsim $
that satisfies our assumptions, and
$\succsim $
that satisfies our assumptions, and
![]() $\varphi (\succsim )(i)$
the location assignment of agent i under this matching. By construction, the matching produced by this mechanism is feasible and
$\varphi (\succsim )(i)$
the location assignment of agent i under this matching. By construction, the matching produced by this mechanism is feasible and
![]() $\bar g$
-acceptable. In addition, the mechanism satisfies two key properties. It is:
$\bar g$
-acceptable. In addition, the mechanism satisfies two key properties. It is:
-
1. constrained efficient in the sense that for all preference vectors
 $\succsim $
that satisfy our assumptions,
$\succsim $
that satisfy our assumptions,
 $\varphi (\succsim )$
is not Pareto dominated by another feasible
$\varphi (\succsim )$
is not Pareto dominated by another feasible
 $\bar g$
-acceptable matching
$\bar g$
-acceptable matching
 $\mu $
. That is, it is not the case that
$\mu $
. That is, it is not the case that
 $\mu (i) \succsim _i \varphi (\succsim )(i)$
for all agents i, and
$\mu (i) \succsim _i \varphi (\succsim )(i)$
for all agents i, and
 $\mu (i) \succ _i \varphi (\succsim )(i)$
for some agent i.
$\mu (i) \succ _i \varphi (\succsim )(i)$
for some agent i. -
2. strategy-proof in the sense that truthful reporting is a dominant strategy of the induced preference reporting game. That is, for every preference vector
 $\succsim $
satisfying our assumptions, every agent i, and every alternative preference
$\succsim $
satisfying our assumptions, every agent i, and every alternative preference
 $\succsim _i'$
that i could report that also satisfies our assumptions,
$\succsim _i'$
that i could report that also satisfies our assumptions,
 $\varphi (\succsim )(i) \succsim _i \varphi (\succsim ^{\prime }_i, \succsim _{-i})(i)$
.
$\varphi (\succsim )(i) \succsim _i \varphi (\succsim ^{\prime }_i, \succsim _{-i})(i)$
.
The proof that the mechanism is constrained efficient and strategy-proof is straightforward, but for completeness, we include it in the SI.
One important property of the canonical priority mechanism that does not carry over to our
![]() $\bar g$
-constrained priority mechanism is the property that the mechanism characterizes the full set of Pareto-efficient assignments. Abdulkadiroglu and Sonmez (Reference Abdulkadiroglu and Sonmez1998) showed that for any Pareto-efficient assignment, there exists an ordering of agents under which implementing the priority mechanism for that ordering generates that assignment. Given this, one could ask whether for every
$\bar g$
-constrained priority mechanism is the property that the mechanism characterizes the full set of Pareto-efficient assignments. Abdulkadiroglu and Sonmez (Reference Abdulkadiroglu and Sonmez1998) showed that for any Pareto-efficient assignment, there exists an ordering of agents under which implementing the priority mechanism for that ordering generates that assignment. Given this, one could ask whether for every
![]() $\bar g$
-constrained efficient assignment, there exists an ordering of the agents for which the
$\bar g$
-constrained efficient assignment, there exists an ordering of the agents for which the
![]() $\bar g$
-constrained priority mechanism generates that assignment. The answer to this question turns out to be no, as demonstrated by the following example with two agents
$\bar g$
-constrained priority mechanism generates that assignment. The answer to this question turns out to be no, as demonstrated by the following example with two agents
![]() $1$
and
$1$
and
![]() $2$
and three locations
$2$
and three locations
![]() $A, B$
, and C. The table gives the ranking of the three locations for each agent and in parentheses the outcome score
$A, B$
, and C. The table gives the ranking of the three locations for each agent and in parentheses the outcome score
![]() $g_i(l)$
for each agent–location pair.
$g_i(l)$
for each agent–location pair.

Suppose that each location has a capacity of 1 seat. If the planner’s threshold
![]() $\bar g$
is set to
$\bar g$
is set to
![]() $0.45$
and agent 1 goes first, then he will be assigned to location A, and agent 2 will be assigned to B. If agent 2 goes first, then she will be assigned to A, and agent
$0.45$
and agent 1 goes first, then he will be assigned to location A, and agent 2 will be assigned to B. If agent 2 goes first, then she will be assigned to A, and agent
![]() $1$
will be sent to C. But the possibility of sending 1 to B and 2 to C also meets the planner’s constraint and is not Pareto dominated by any other assignment that is acceptable to the planner.
$1$
will be sent to C. But the possibility of sending 1 to B and 2 to C also meets the planner’s constraint and is not Pareto dominated by any other assignment that is acceptable to the planner.
3 Applications
To illustrate the mechanism, we apply it to both simulated data and two empirical examples using real-world data from the United States that involve the assignment of refugees to resettlement locations and the assignment of students to schools.Footnote 11
Our mechanism requires the planner to select a value for
![]() $\bar g$
, and this choice implies a trade-off between an outcome-based and preference-based matching. From the planner’s perspective, it is desirable to achieve the highest possible value of
$\bar g$
, and this choice implies a trade-off between an outcome-based and preference-based matching. From the planner’s perspective, it is desirable to achieve the highest possible value of
![]() $\bar g$
to ensure that the agents’ outcomes are optimized. However, setting a higher value of
$\bar g$
to ensure that the agents’ outcomes are optimized. However, setting a higher value of
![]() $\bar g$
comes at the cost of assigning agents to locations that are, in expectation, lower in their preference rankings. That is, while the mechanism simultaneously considers both outcomes and preferences, there is a trade-off between the two, where the balance of that trade-off changes as
$\bar g$
comes at the cost of assigning agents to locations that are, in expectation, lower in their preference rankings. That is, while the mechanism simultaneously considers both outcomes and preferences, there is a trade-off between the two, where the balance of that trade-off changes as
![]() $\bar g$
increases.
$\bar g$
increases.
The magnitude of the trade-off also depends upon the joint distribution of agents’ preference rankings and their outcome scores. Two measures, in particular, play an important role: the correlation between outcome scores and preference rankings within agents (i.e., the degree to which an agent’s preferred locations align with the locations where that agent would achieve their best outcomes) and the correlation between preference rankings across agents (i.e., the degree to which agents have similar preference rankings). We demonstrate this below.
3.1 Simulation Data
We apply the mechanism to simulated data to show these properties. For simplicity, our simulations involve assigning 100 agents to 100 locations with one seat each. For each agent, we randomly generate a preference rank vector (with
![]() $1$
indicating the most desired location and
$1$
indicating the most desired location and
![]() $100$
the worst) and an outcome score vector (with values in
$100$
the worst) and an outcome score vector (with values in
![]() $[0,1]$
). The simulations vary both the correlation between preference and outcome vectors (
$[0,1]$
). The simulations vary both the correlation between preference and outcome vectors (
![]() $-0.5$
,
$-0.5$
,
![]() $0$
, and
$0$
, and
![]() $0.5$
) and the correlation between preference vectors across agents (
$0.5$
) and the correlation between preference vectors across agents (
![]() $0$
,
$0$
,
![]() $0.5$
, and
$0.5$
, and
![]() $0.8$
).Footnote
12
This yields nine different scenarios, and in each, we apply our mechanism to make the assignment for various values of
$0.8$
).Footnote
12
This yields nine different scenarios, and in each, we apply our mechanism to make the assignment for various values of
![]() $\bar g$
. See the SI for details.
$\bar g$
. See the SI for details.
3.2 Refugee Data
As a simulated illustration of how the mechanism could perform in a real-world scenario, we apply it to data from refugees in the United States, where refugee families are the agents and resettlement cities are the locations. Early employment is a core goal of the U.S. resettlement program, which strives to quickly transition refugees into self-sufficiency after arrival. This application illustrates how our mechanism could hypothetically be employed in the United States to achieve a desired level of early employment while geographically assigning refugees based on their location preferences.
Our real-world refugee data include deidentified information on working-age refugees (ages 18–64; N = 33,782) who have been resettled to the United States during the 2011–2016 period by one of the largest U.S. refugee resettlement agencies. Over this time period, the agencies’ placement officers centrally assigned refugees to one of approximately 40 resettlement locations in the agency’s network. The data contain details on the refugee characteristics such as age, gender, origin, and education. The data also include the assigned resettlement location, whether the refugee was employed at 90 days after arrival, and whether the refugee migrated from the initial location within 90 days.
We applied our mechanism to data on the refugee families who arrived in the third quarter (Q3) of 2016, specifically focusing on refugees who were free to be assigned to different resettlement locations (561 families), in contrast to refugees who were predestined to specific locations on the basis of existing family or other ties. To generate each family’s outcome score vector across each of the locations, we employed the same methodology in Bansak et al. (Reference Bansak2018), using the data for the refugees who arrived from 2011 up to (but not including) 2016 Q3 to generate models that predict the expected employment success of a family (i.e., the mean probability of finding employment among working-age members of the family) at any of the locations, as a function of their background characteristics. These models were then applied to the families who arrived in 2016 Q3 to generate their predicted employment success at each location, which comprise their outcome score vectors. See the SI and Bansak et al. (Reference Bansak2018) for details.
Our mechanism also requires data on location preferences of refugees. To the best of our knowledge, such data do not currently exist in the United States, where refugees are assigned to locations by the resettlement agencies. We therefore infer revealed location preferences from secondary migration behavior. Specifically, we use the same modeling procedures used in the outcome score estimation, simply swapping in outmigration in place of employment as the response variable. This allows us to predict for each refugee family that arrived in 2016 Q3 the probability of outmigration at each location as a function of their background characteristics. For each family, we then rank locations such that the location with the lowest (highest) probability of outmigration is ranked first (last). Details about the data and sample are provided in the SI.
We acknowledge that inferred location preferences from secondary migration behavior are not necessarily the same as the stated location preferences that refugees would express in an application form if given the opportunity to do so by host country governments. That said, there are reasons to believe that the inferred location preferences provide a useful proxy. Outmigration is a costly signal indicating that a refugee prefers to move rather than stay in the originally assigned location. Mossad et al. (Reference Mossad, Ferwerda, Lawrence, Weinstein and Hainmueller2020) provide a comprehensive analysis of the secondary migration patterns of refugees in the United States and find that secondary migration is mostly driven by refugees relocating in search of employment opportunities and coethnic communities. One of the main channels through which these effects operate is the refugee’s nationality, which is also an important predictor in the model that we use to infer revealed location preferences from secondary migration.
3.3 Education Data
As a second simulated illustration of how the mechanism could perform in a real-world scenario, we apply it to education data from the United States, where the agents are individual students and the locations are schools. In particular, we consider data from the Tennessee’s Student Teacher Achievement Ratio (STAR) project conducted by the Tennessee State Department of Education (for details, see Achilles et al. Reference Achilles2008). These data contain information on the choice of elementary schools for a large sample of students as well as information on the test score performance of these students. We focus on the Kindergarten grade level and apply our mechanism to generate new assignments of students to schools with the goal of improving the outcomes of students as measured by standardized tests administered at the end of Kindergarten. One could imagine a school district setting a minimum test score that should be achieved on average.
To generate each student’s outcome score vector across each of the schools, we employ the same methods as in the previous application to predict the expected test scores of a student at any of the schools, as a function of their background characteristics. The background characteristics included the students’ age, gender, and race, as well as information on whether they are eligible for free school lunches (a proxy for socioeconomic status) or special education. The test score outcome was defined as the sum of reading, math, and listening scaled scores on the SAT for the Kindergarten level.
We inferred revealed school preferences of students from the observed transfers out of the schools. Specifically, we used the same modeling procedure as for the test scores but instead used a response variable that measured whether a student had transferred to another school by the first, second, or third grade. Based on these models, we can then predict for each student the propensity for leaving each school as a function of their background characteristics. For each student, we then rank schools such that the school for which they have the lowest (highest) propensity for transferring out is ranked first (last).
We generate these outcome score and preference vectors and apply our mechanism to a random sample of 1,000 students from 33 schools that are observed for all grades from Kindergarten through third grade and have nonmissing data for tests scores and background characteristics. Details about the data and sample are provided in the SI.
4 Results
4.1 Simulated Data
Figure 1 depicts the results for assignment under the
![]() $\bar g$
-constrained priority mechanism for nine different simulation scenarios that vary the correlation between preferences and outcome scores within agents and the correlation between preferences across agents. In addition, to model a real-world scenario in which agents can indicate only a limited number of top locations in an application form, the preference vectors are truncated such that only the top 10 ranks are retained and indifference is established among the remaining location. The top panel shows the proportion of agents who were assigned to one of their top-three locations given various levels of
$\bar g$
-constrained priority mechanism for nine different simulation scenarios that vary the correlation between preferences and outcome scores within agents and the correlation between preferences across agents. In addition, to model a real-world scenario in which agents can indicate only a limited number of top locations in an application form, the preference vectors are truncated such that only the top 10 ranks are retained and indifference is established among the remaining location. The top panel shows the proportion of agents who were assigned to one of their top-three locations given various levels of
![]() $\bar g$
, the threshold for the minimum average outcome score. The bottom panel shows the mean outcome score for agents in their assigned locations for the same levels of
$\bar g$
, the threshold for the minimum average outcome score. The bottom panel shows the mean outcome score for agents in their assigned locations for the same levels of
![]() $\bar g$
. The curves end once
$\bar g$
. The curves end once
![]() $\bar g^{\max }$
has been reached, and hence no feasible assignment is possible.
$\bar g^{\max }$
has been reached, and hence no feasible assignment is possible.

Figure 1 Results from applying our
![]() $\bar g$
-constrained priority mechanism to simulated data that varies the correlations between preference and outcome score vectors and the correlations between preference vectors Across agents. Upper panel shows the average probability that an agent was assigned to one of its top-three locations. Lower panel shows the realized average outcome score.
$\bar g$
-constrained priority mechanism to simulated data that varies the correlations between preference and outcome score vectors and the correlations between preference vectors Across agents. Upper panel shows the average probability that an agent was assigned to one of its top-three locations. Lower panel shows the realized average outcome score.
![]() $N=100$
.
$N=100$
.
There is a clear trade-off between realized preference ranks and outcome scores in all simulations. As
![]() $\bar g$
is increased, the realized mean outcome score eventually increases. This is a mechanical result of increasing
$\bar g$
is increased, the realized mean outcome score eventually increases. This is a mechanical result of increasing
![]() $\bar g$
and hence enforcing the requirement for a higher mean outcome value. Simultaneously, as soon as the mean outcome score is impacted, the proportion of agents assigned to one of their preferred locations also begins to decrease. This occurs because enforcing the requirement for a higher value of
$\bar g$
and hence enforcing the requirement for a higher mean outcome value. Simultaneously, as soon as the mean outcome score is impacted, the proportion of agents assigned to one of their preferred locations also begins to decrease. This occurs because enforcing the requirement for a higher value of
![]() $\bar g$
requires the mechanism to deviate from the preference-based optimization.
$\bar g$
requires the mechanism to deviate from the preference-based optimization.
Figure 1 also shows how the immediacy and severity of the trade-off can vary substantially depending upon the joint distribution of preferences and outcome scores.Footnote
13
First, focusing on the top panel, we see that the higher the correlation between agents’ preferences, the worse is the achievable baseline proportion of agents that can be assigned to one of their top locations at the lowest values of
![]() $\bar g$
. This result, which holds regardless of the correlation between preferences and outcome scores, is intuitive: the more similar are different agents’ preferences, the more rivalrous is the matching procedure, and hence the more difficult it is to match agents to one of their top-ranked locations given limited capacity in each location.
$\bar g$
. This result, which holds regardless of the correlation between preferences and outcome scores, is intuitive: the more similar are different agents’ preferences, the more rivalrous is the matching procedure, and hence the more difficult it is to match agents to one of their top-ranked locations given limited capacity in each location.
Second, the more positive the correlation between preferences and outcome scores, the less severe is the trade-off in the sense that the trade-off does not kick in until higher levels of
![]() $\bar g$
are enforced. The intuition for this result is that if preferences and outcomes are positively correlated, then matching based on preferences should indirectly also lead to outcome-based matching, and hence deviation from the preference-based solution will not occur until a higher level of
$\bar g$
are enforced. The intuition for this result is that if preferences and outcomes are positively correlated, then matching based on preferences should indirectly also lead to outcome-based matching, and hence deviation from the preference-based solution will not occur until a higher level of
![]() $\bar g$
is reached. This is a useful finding from the standpoint of a real-world implementation of the mechanism. If, in advance of their preference reporting, agents were given information on their predicted outcomes in each location, they could incorporate such information into their preference determination. If this results in a closer alignment of preferences and outcomes, that would help alleviate the trade-off in the mechanism.
$\bar g$
is reached. This is a useful finding from the standpoint of a real-world implementation of the mechanism. If, in advance of their preference reporting, agents were given information on their predicted outcomes in each location, they could incorporate such information into their preference determination. If this results in a closer alignment of preferences and outcomes, that would help alleviate the trade-off in the mechanism.
Third, turning to the bottom panel in Figure 1, we see that once the trade-off kicks in, the realized mean outcome curves trace closely along the identity line; that is, upon enforcing a level of
![]() $\bar g$
that deviates from the preference-based assignment, the mechanism will find an alternative assignment that optimizes for preferences subject to just barely satisfying the
$\bar g$
that deviates from the preference-based assignment, the mechanism will find an alternative assignment that optimizes for preferences subject to just barely satisfying the
![]() $\bar g$
constraint. The realized mean outcome results also mirror the trends on realized preference ranks: the more positive is the correlation between preference and outcome vectors, the later the trade-off kicks in.
$\bar g$
constraint. The realized mean outcome results also mirror the trends on realized preference ranks: the more positive is the correlation between preference and outcome vectors, the later the trade-off kicks in.
Fourth, we see that given a negative correlation between preferences and outcome scores, the correlation across preference vectors has a significant impact on how the trade-off affects the realized mean outcome score, with the trade-off being more severe with a low correlation across preference vectors. This result can be explained as follows. A negative correlation between preference and outcome vectors implies that preference-based assignment is counter to the goal of optimizing for realized outcome scores. However, if there is also a positive correlation across agents’ preferences, that means that different kinds of agents generally prefer the same locations, and hence also that the locations that result in low outcome scores are also similar across agents, thus limiting the degree to which matching based on preferences will actually hurt realized outcome scores on average. If, in contrast, there is no correlation across preferences, then there is greater latitude for the mechanism to assign agents to their higher-ranked locations, which also happen to be the locations that are the worst for their outcome scores. As the correlation between preference and outcome vectors becomes more positive, this dynamic begins to disappear. However, the reason it does not reverse in the bottom-right panel of Figure 1 is due to the existence of trailing indifferences in the preference rank vectors, which means the agents who could not be matched to one of their strictly ranked locations are assigned using outcome-based optimization, thereby limiting the effect of the phenomenon described above.Footnote 14
4.2 Refugee Data
Figure 2 shows features of the joint distribution of the refugee families’ outcome score and preference rank vectors. The top panel pertains to the correlation between the families’ outcome and preference vectors. For each family, a correlation is computed between its two vectors, and the panel displays the distribution of those correlations. The distribution is roughly centered around zero (the mean correlation is
![]() $0.03$
). This suggests a relatively limited relationship between the locations refugees prefer and those where they would actually achieve better employment outcomes. This is an interesting finding and also has a key policy implication. Providing refugees with information on which locations are beneficial for their employment outcomes would allow them to formulate more informed preferences. If this results in a closer correlation between preference and outcome vectors, this would help strengthen our mechanism, since a more positive correlation alleviates the trade-off between outcome- and preference-based matching.
$0.03$
). This suggests a relatively limited relationship between the locations refugees prefer and those where they would actually achieve better employment outcomes. This is an interesting finding and also has a key policy implication. Providing refugees with information on which locations are beneficial for their employment outcomes would allow them to formulate more informed preferences. If this results in a closer correlation between preference and outcome vectors, this would help strengthen our mechanism, since a more positive correlation alleviates the trade-off between outcome- and preference-based matching.

Figure 2 Distribution of pairwise correlations between refugee family location preferences, integration outcomes (i.e., employment), and preferences and outcomes.
![]() $N=561$
refugee families who arrived in the United States in Q3 of 2016.
$N=561$
refugee families who arrived in the United States in Q3 of 2016.
The middle panel in Figure 2 shows the distribution of pairwise correlations between families’ preference vectors. The correlations are mostly highly positive, with a mean correlation of
![]() $0.67$
. This shows that preference vectors are relatively similar across the families; many refugees would more or less prefer to be placed in similar locations. Given the existence of location capacity constraints, this is an inconvenient finding from the standpoint of preference-based assignment.
$0.67$
. This shows that preference vectors are relatively similar across the families; many refugees would more or less prefer to be placed in similar locations. Given the existence of location capacity constraints, this is an inconvenient finding from the standpoint of preference-based assignment.
The bottom panel in Figure 3 shows the distribution of all pairwise correlations between families’ outcome vectors. As can be seen, the correlations are overwhelmingly positive (with a mean correlation of
![]() $0.75$
), highlighting the fact already shown elsewhere (Bansak et al. Reference Bansak2018) that certain locations are generally better than other locations for helping refugees to achieve positive employment outcomes. However, the fact that there is still meaningful variation across different families’ outcome score vectors indicates that certain locations do indeed make a better match for different refugee families, depending on their personal characteristics, which is the foundation for the outcome-optimization matching procedure introduced by Bansak et al. (Reference Bansak2018).
$0.75$
), highlighting the fact already shown elsewhere (Bansak et al. Reference Bansak2018) that certain locations are generally better than other locations for helping refugees to achieve positive employment outcomes. However, the fact that there is still meaningful variation across different families’ outcome score vectors indicates that certain locations do indeed make a better match for different refugee families, depending on their personal characteristics, which is the foundation for the outcome-optimization matching procedure introduced by Bansak et al. (Reference Bansak2018).

Figure 3 Results of applying the
![]() $\bar g$
-constrained priority mechanism to refugee families in the United States for various specified thresholds for the expected minimum level of average integration outcomes (
$\bar g$
-constrained priority mechanism to refugee families in the United States for various specified thresholds for the expected minimum level of average integration outcomes (
![]() $\bar g$
). Upper panel shows the average probability that a refugee family got assigned to one of their top-three locations. Lower panel shows the realized average integration outcomes, i.e., the average projected probability of employment.
$\bar g$
). Upper panel shows the average probability that a refugee family got assigned to one of their top-three locations. Lower panel shows the realized average integration outcomes, i.e., the average projected probability of employment.
![]() $N=561$
families who arrived in Q3 of 2016.
$N=561$
families who arrived in Q3 of 2016.
In applying our mechanism to the 2016 Q3 refugee data, we impose real-world assignment constraints, giving each location capacity for the same number of families as were sent to those locations in actuality. We also truncate each family’s preference vectors such that only the first 10 ranks are retained and indifference is established among the remaining locations.
Figure 3 displays the results of applying our mechanism. As before, the mechanism is applied at various levels of
![]() $\bar g$
, which is denoted by the x-axis. The y-axis of the top panel denotes the proportion of cases assigned to one of their top-three locations, whereas the y-axis in the bottom panel denotes the mean realized outcome score, i.e., the average predicted probability of employment, based on the assignment. The two dashed vertical lines highlight the trade-off interval, where altering the value of
$\bar g$
, which is denoted by the x-axis. The y-axis of the top panel denotes the proportion of cases assigned to one of their top-three locations, whereas the y-axis in the bottom panel denotes the mean realized outcome score, i.e., the average predicted probability of employment, based on the assignment. The two dashed vertical lines highlight the trade-off interval, where altering the value of
![]() $\bar g$
impacts both preferences and outcomes, and the interval ends when
$\bar g$
impacts both preferences and outcomes, and the interval ends when
![]() $\bar g$
is raised above
$\bar g$
is raised above
![]() $\bar g^{\max }$
.
$\bar g^{\max }$
.
Given a predominantly preference-based assignment (i.e., setting
![]() $\bar g$
to any value below the value at which the trade-off interval begins), a mean outcome score of
$\bar g$
to any value below the value at which the trade-off interval begins), a mean outcome score of
![]() $0.41$
is achieved, meaning the predicted average employment rate is 41%.Footnote
15
Under this assignment, about 25% of refugee families are assigned to a location that is among their top-three choices. For comparison, the average observed employment rate for families at their actual locations without applying any mechanism was 34%. This suggests that there are significant synergies between refugees and locations in the sense that certain locations are a better match for different refugees, depending on their personal characteristics. Even under a predominantly preference-based assignment, the mechanism can therefore increase the predicted average employment rate to
$0.41$
is achieved, meaning the predicted average employment rate is 41%.Footnote
15
Under this assignment, about 25% of refugee families are assigned to a location that is among their top-three choices. For comparison, the average observed employment rate for families at their actual locations without applying any mechanism was 34%. This suggests that there are significant synergies between refugees and locations in the sense that certain locations are a better match for different refugees, depending on their personal characteristics. Even under a predominantly preference-based assignment, the mechanism can therefore increase the predicted average employment rate to
![]() $41\%$
, about a 20% increase over the mean employment rate observed without applying any mechanism.
$41\%$
, about a 20% increase over the mean employment rate observed without applying any mechanism.
On the opposite end of the spectrum, a purely outcome-driven optimization would yield the highest feasible
![]() $\bar g$
(
$\bar g$
(
![]() $\bar g^{\max }$
), which is just below
$\bar g^{\max }$
), which is just below
![]() $0.52$
, i.e., a predicted average employment rate of 52%.Footnote
16
This amounts to about a 53% increase over the mean employment rate observed without applying any mechanism. Therefore, if all the government cared about for the assignment was to maximize the score, it could attain a considerably higher predicted employment rate by enforcing
$0.52$
, i.e., a predicted average employment rate of 52%.Footnote
16
This amounts to about a 53% increase over the mean employment rate observed without applying any mechanism. Therefore, if all the government cared about for the assignment was to maximize the score, it could attain a considerably higher predicted employment rate by enforcing
![]() $\bar g^{\max }$
. Yet, at
$\bar g^{\max }$
. Yet, at
![]() $\bar g^{\max }$
, only 15% of refugee families would be assigned to one of their top-three locations. The preference curve in the top panel features a gradient that gradually steepens, with the trade-off becoming increasingly more severe as
$\bar g^{\max }$
, only 15% of refugee families would be assigned to one of their top-three locations. The preference curve in the top panel features a gradient that gradually steepens, with the trade-off becoming increasingly more severe as
![]() $\bar g$
is increased.
$\bar g$
is increased.
Finally, we also employed an alternative method to estimate location preferences that attempts to correct for potential bias due to relocation costs. As described, we are inferring location preferences from outmigration behavior. However, outmigration decisions are a function of two primary components: a family’s desire to leave and their ability to leave. It is the former component that captures preferences and hence what is of primary interest for our purposes, but it is possible that differential costs of leaving and relocating across different locations have an effect on outmigration patterns via the latter component. With only observational behavioral data, it is difficult to perfectly decompose these two components. However, we attempt to do so by estimating a structural model of outmigration designed to capture geographic and economic factors that relate to the costs of relocation, and then by using this structural model to adjust our original preference estimates such that our new preference estimates are, in theory, driven more strictly by the preference component of outmigration behavior. We then reapply our mechanism to the 2016 Q3 refugee data with the new preferences substituted in. The results, which are provided in the SI, display a similar pattern as when the original preference estimates are employed with one main difference: the proportion of families assigned to one of their estimated top-three locations is systematically lower at all levels of
![]() $\bar g$
, which is the result of the families’ top-ranked locations being more rivalrous (more highly correlated) according to the alternative preference estimates. More details about the methodology and the results are provided in the SI.
$\bar g$
, which is the result of the families’ top-ranked locations being more rivalrous (more highly correlated) according to the alternative preference estimates. More details about the methodology and the results are provided in the SI.
4.3 Education Data
We now turn to the results for the application of the mechanism to the education data from Tennessee, where we assigned students to elementary schools to optimize on test scores and students’ preferences over schools.
Figure 4 shows features of the joint distribution of the students’ outcome score and preference rank vectors. The top panel pertains to the correlation between the students’ outcome and preference vectors. We see that for most students, the correlations are modest but positive with a mean of
![]() $0.11$
, indicating that the students slightly prefer schools where they are predicted to have higher test scores. As mentioned earlier, a positive correlation between preference and outcome vectors somewhat alleviates the trade-off between outcome- and preference-based matching. That said, as shown in the middle panel in Figure 4, the distribution of pairwise correlations between students’ preference vectors are tightly clustered around a high positive mean correlation of
$0.11$
, indicating that the students slightly prefer schools where they are predicted to have higher test scores. As mentioned earlier, a positive correlation between preference and outcome vectors somewhat alleviates the trade-off between outcome- and preference-based matching. That said, as shown in the middle panel in Figure 4, the distribution of pairwise correlations between students’ preference vectors are tightly clustered around a high positive mean correlation of
![]() $0.93$
. This shows that students mostly prefer to be placed in similar schools, which makes the preference-based matching assignment more rivalrous given a fixed number of seats in the preferred schools. As shown in the bottom panel in Figure 4, we also find that the pairwise correlations between students’ outcome vectors are almost all positive (with a mean correlation of
$0.93$
. This shows that students mostly prefer to be placed in similar schools, which makes the preference-based matching assignment more rivalrous given a fixed number of seats in the preferred schools. As shown in the bottom panel in Figure 4, we also find that the pairwise correlations between students’ outcome vectors are almost all positive (with a mean correlation of
![]() $0.79$
), which suggests that certain schools are generally better than other schools for students to achieve higher test scores.
$0.79$
), which suggests that certain schools are generally better than other schools for students to achieve higher test scores.

Figure 4 Distribution of pairwise correlations between student preferences over elementary schools, test score outcomes, and preferences and outcomes.
![]() $N=1000$
randomly sampled students from Tennessee Project STAR data.
$N=1000$
randomly sampled students from Tennessee Project STAR data.
In applying our mechanism to these education data, we impose the same real-world assignment constraints as before, giving each school capacity for the same number of students as were enrolled in those schools in actuality. We also truncate each student’s preference vectors such that only the first 10 ranks are retained and indifference is established among the remaining schools in order to mimic a situation on an application form where students can rank only the top-ten preferred schools.
Figure 5 displays the results of applying our mechanism. As before, the mechanism is applied at various levels of
![]() $\bar g$
, which is denoted by the x-axis. The y-axis of the top panel denotes the proportion of students assigned to one of their top-three schools, whereas the y-axis in the bottom panel denotes the mean realized outcome score, i.e., the average predicted test score, based on the assignment. The two dashed vertical lines highlight the trade-off interval, where altering the value of
$\bar g$
, which is denoted by the x-axis. The y-axis of the top panel denotes the proportion of students assigned to one of their top-three schools, whereas the y-axis in the bottom panel denotes the mean realized outcome score, i.e., the average predicted test score, based on the assignment. The two dashed vertical lines highlight the trade-off interval, where altering the value of
![]() $\bar g$
impacts both preferences and outcomes, and the interval ends when
$\bar g$
impacts both preferences and outcomes, and the interval ends when
![]() $\bar g$
is raised above
$\bar g$
is raised above
![]() $\bar g^{\max }$
.
$\bar g^{\max }$
.

Figure 5 Results of applying the
![]() $\bar g$
-constrained priority mechanism to student assignment to elementary schools for various specified thresholds for the expected minimum level of average test score outcomes (
$\bar g$
-constrained priority mechanism to student assignment to elementary schools for various specified thresholds for the expected minimum level of average test score outcomes (
![]() $\bar g$
). Upper panel shows the average probability that a student got assigned to one of their top-three schools. Lower panel shows the realized average test score outcomes, i.e., the average projected SAT score.
$\bar g$
). Upper panel shows the average probability that a student got assigned to one of their top-three schools. Lower panel shows the realized average test score outcomes, i.e., the average projected SAT score.
![]() $N=1000$
randomly sampled students from Tennessee Project STAR data.
$N=1000$
randomly sampled students from Tennessee Project STAR data.
Given a predominantly preference-based assignment (i.e., setting
![]() $\bar g$
to any value below the value at which the trade-off interval begins), a mean predicted test score outcome of
$\bar g$
to any value below the value at which the trade-off interval begins), a mean predicted test score outcome of
![]() $1,502$
is achieved. Under this assignment, about
$1,502$
is achieved. Under this assignment, about
![]() $42\%$
of students are assigned to a school that is among their top-three choices.Footnote
17
For comparison, the average observed test score for the students at their actual locations without applying the mechanism was about
$42\%$
of students are assigned to a school that is among their top-three choices.Footnote
17
For comparison, the average observed test score for the students at their actual locations without applying the mechanism was about
![]() $1,490$
with a standard deviation of
$1,490$
with a standard deviation of
![]() $86$
. This suggests that, as with the refugee data above, there are significant synergies between students and schools in the sense that certain schools are a better match for different students, depending on their personal characteristics. Even under a predominantly preference-based assignment, the mechanism can therefore increase the predicted average test score to
$86$
. This suggests that, as with the refugee data above, there are significant synergies between students and schools in the sense that certain schools are a better match for different students, depending on their personal characteristics. Even under a predominantly preference-based assignment, the mechanism can therefore increase the predicted average test score to
![]() $1,502$
, a meaningful improvement of about a seventh of a standard deviation in test scores compared to the observed mean under the actual assignments.
$1,502$
, a meaningful improvement of about a seventh of a standard deviation in test scores compared to the observed mean under the actual assignments.
On the opposite end of the spectrum, a purely outcome-driven optimization would yield the highest feasible
![]() $\bar g$
(
$\bar g$
(
![]() $\bar g^{\max }$
), which is a mean predicted test score outcome of
$\bar g^{\max }$
), which is a mean predicted test score outcome of
![]() $1,519$
. A fully outcome-based matching of students to schools can therefore result in a sizable increase in the predicted average test score of about a third of a standard deviation in test scores compared to the observed mean under the actual assignments. Given the trade-off between preference-based and outcome-based matching, this means that under a purely outcome-driven optimization, only about
$1,519$
. A fully outcome-based matching of students to schools can therefore result in a sizable increase in the predicted average test score of about a third of a standard deviation in test scores compared to the observed mean under the actual assignments. Given the trade-off between preference-based and outcome-based matching, this means that under a purely outcome-driven optimization, only about
![]() $10\%$
of students would be assigned to a school that is among their top-three choices. This highlights that compared to the refugee application, the trade-off in this education example is somewhat more severe, which is expected given that the preferences are more concentrated on similar schools even though there is a somewhat more positive correlation between preferences and outcomes.
$10\%$
of students would be assigned to a school that is among their top-three choices. This highlights that compared to the refugee application, the trade-off in this education example is somewhat more severe, which is expected given that the preferences are more concentrated on similar schools even though there is a somewhat more positive correlation between preferences and outcomes.
5 Other Welfare Concerns
One possible concern with our mechanism is that if agents whose preferences are not highly correlated with their outcome scores are given higher priority than others, then their assignments could lower the overall preference rank of locations assigned to agents who have lower priority. As an example, besides worrying about achieving a constrained Pareto-efficient allocation, suppose the planner also cares about the percentage of agents who are awarded one of their top-three ranked locations. Let us refer to this welfare metric as the “top-3 metric.” Just how much improvement on this metric can be achieved by changing the order in which families are assigned?
To get a sense of this, we took a random sampling of the different possible orderings of agents and study the variation generated in the top-3 metric. We reran a subset of the nine simulation scenarios considered in Section 4.1, generating the data using identical procedures and employing the same parameters (number of agents, number of locations, size of indifference sets, and levels of
![]() $\bar g$
). However, at each level of
$\bar g$
). However, at each level of
![]() $\bar g$
considered in each scenario, we apply the mechanism to the simulated data
$\bar g$
considered in each scenario, we apply the mechanism to the simulated data
![]() $100$
separate times, where the order of the agents is rerandomized each time. The results are shown in the SI. With respect to the proportion assigned to a top-three location, the difference between the maximum and minimum ranges from 0.05 to 0.18 with a median difference of 0.13.Footnote
18
Thus, reordering could produce a typical improvement on the top-3 metric over the typical draw by several percentage points in these data.
$100$
separate times, where the order of the agents is rerandomized each time. The results are shown in the SI. With respect to the proportion assigned to a top-three location, the difference between the maximum and minimum ranges from 0.05 to 0.18 with a median difference of 0.13.Footnote
18
Thus, reordering could produce a typical improvement on the top-3 metric over the typical draw by several percentage points in these data.
One limitation of this exercise, however, is because the
![]() $\bar g$
-constrained priority mechanism does not characterize the set of constrained Pareto-efficient assignments (as we showed by example in Section 2.3), we do not know if there are constrained efficient assignments that yield improvements even beyond the ones we can generate by reordering the families and applying our mechanism. We also do not know if there is a strategy-proof constrained-efficient mechanism that picks out the assignment that maximizes the top-3 metric among those that can be generated by reordering the agents under our constrained priority mechanism—let alone an assignment that cannot be generated by reordering. It is obvious that the mechanism defined by successively reordering and then selecting the one that maximizes the top-3 metric does not define a strategy-proof mechanism. If the planner is willing to sacrifice strategy-proofness, she could attempt to target the best assignment that could be generated using our constrained priority mechanism by successively reordering the agents. But by implementing this approach, agents may have an incentive to falsify their preferences, and hence the best assignment(s) the planner is trying to target may no longer even be generated.
$\bar g$
-constrained priority mechanism does not characterize the set of constrained Pareto-efficient assignments (as we showed by example in Section 2.3), we do not know if there are constrained efficient assignments that yield improvements even beyond the ones we can generate by reordering the families and applying our mechanism. We also do not know if there is a strategy-proof constrained-efficient mechanism that picks out the assignment that maximizes the top-3 metric among those that can be generated by reordering the agents under our constrained priority mechanism—let alone an assignment that cannot be generated by reordering. It is obvious that the mechanism defined by successively reordering and then selecting the one that maximizes the top-3 metric does not define a strategy-proof mechanism. If the planner is willing to sacrifice strategy-proofness, she could attempt to target the best assignment that could be generated using our constrained priority mechanism by successively reordering the agents. But by implementing this approach, agents may have an incentive to falsify their preferences, and hence the best assignment(s) the planner is trying to target may no longer even be generated.
5.1 Using Predicted Preferences
An alternative approach to capturing part of the gains that we are seeing from reordering the agents that does not sacrifice either strategy-proofness or constrained efficiency is to use historical (or other) data to predict the preferences of the agents. For example, the planner could use historical data to predict preferences based on the demographic similarities of past agents to current ones and fix the ordering of agents to be the one that maximizes the top-3 metric according to the predicted preferences.Footnote 19 In particular, note that if the planner can perfectly predict the preferences of agents, then strategy-proofness is not a concern, since the planner already has the agents’ preferences. In this case, the planner can recover the full gain from rerandomizing the order of agents. If the planner cannot perfectly predict the preferences of the agents, but can come close, then the planner should, in expectation, be able to recover some of this gain. Note that because we are using historical data from past agents to set the order of the current agents, the agents cannot use their reported preferences to manipulate the mechanism.
In order to evaluate this approach, we employed the data from our refugee application described earlier. Specifically, we began by randomly drawing 100 families from the full set of data used in the application. We then randomly generated 100 different orderings of those families, and for each ordering, we implemented the constrained priority mechanism along a sequence of values of
![]() $\bar g$
. We used the families’ outcome score vectors and “actual” preference vectors (i.e., the preference vectors employed in the application presented earlier). This allows us to asses the extent to which different orderings can result in varying levels of the top-3 metric. The components of Figure 6 labeled “Many Orders” display these results, with the black dots corresponding to the average across the 100 orderings and the intervals denoting the maximum and minimum results obtained across the 100 orderings.
$\bar g$
. We used the families’ outcome score vectors and “actual” preference vectors (i.e., the preference vectors employed in the application presented earlier). This allows us to asses the extent to which different orderings can result in varying levels of the top-3 metric. The components of Figure 6 labeled “Many Orders” display these results, with the black dots corresponding to the average across the 100 orderings and the intervals denoting the maximum and minimum results obtained across the 100 orderings.

Figure 6 Results from applying our
![]() $\bar g$
-constrained priority mechanism to 100 random orderings of a random sample of 100 families from the 2016 Q3 refugee data, along with “best guess” ordering based on pseudo preferences. The black dots correspond to the average results across the 100 orderings, and the intervals denote the maximum and minimum results obtained across the 100 orderings. The triangles (labeled “Pseudo-Inferred Order”) denote the actual results when employing the ordering that yielded the best pseudo top-3 metric according to the pseudo preferences. The three scenarios successively increase the amount of perturbation applied to the actual preference vectors to generate the pseudo preferences. Upper panel shows the average probability that an agent was assigned to one of its top-three locations. Lower panel shows the realized average outcome score.
$\bar g$
-constrained priority mechanism to 100 random orderings of a random sample of 100 families from the 2016 Q3 refugee data, along with “best guess” ordering based on pseudo preferences. The black dots correspond to the average results across the 100 orderings, and the intervals denote the maximum and minimum results obtained across the 100 orderings. The triangles (labeled “Pseudo-Inferred Order”) denote the actual results when employing the ordering that yielded the best pseudo top-3 metric according to the pseudo preferences. The three scenarios successively increase the amount of perturbation applied to the actual preference vectors to generate the pseudo preferences. Upper panel shows the average probability that an agent was assigned to one of its top-three locations. Lower panel shows the realized average outcome score.
![]() $N=100$
.
$N=100$
.
Furthermore, for each of the 100 orderings, we also evaluated the results of applying the constrained priority mechanism using pseudo-preference vectors in place of the actual preference vectors. These pseudo-preference vectors are intended to represent the imperfectly predicted preferences of the agents. At each level of
![]() $\bar g$
, we identified the random ordering that resulted in the best pseudo aggregate welfare as measured by the fraction of families receiving one of their top-three locations according to these pseudo preferences. We were then able to assess the actual welfare results (based on the families’ actual preferences) of applying these “best guess” orderings. In order words, we ran through the process by which a researcher could (i) in advance/independent of actual preference reporting employ simulations to identify orderings likely to lead to higher levels of aggregate welfare based on predicted preferences and then (ii) use those as the final orderings by which to actually apply the
$\bar g$
, we identified the random ordering that resulted in the best pseudo aggregate welfare as measured by the fraction of families receiving one of their top-three locations according to these pseudo preferences. We were then able to assess the actual welfare results (based on the families’ actual preferences) of applying these “best guess” orderings. In order words, we ran through the process by which a researcher could (i) in advance/independent of actual preference reporting employ simulations to identify orderings likely to lead to higher levels of aggregate welfare based on predicted preferences and then (ii) use those as the final orderings by which to actually apply the
![]() $\bar g$
-constrained priority mechanism to assign the families.
$\bar g$
-constrained priority mechanism to assign the families.
To simulate the process of imperfectly predicting the families’ pseudo preferences, we constructed their pseudo preference vectors by randomly perturbing their actual preference vectors. In order to investigate the performance of this approach across different levels of effectiveness in predicting preferences (i.e., the extent to which it is possible to construct pseudo preference vectors that are similar to the actual preference vectors), we imposed varying degrees of perturbation and evaluated the results across those different specifications. The results can be seen in the components labeled “Pseudo-Inferred Order” in Figure 6, where the separate panels correspond to scenarios with increasing amounts of perturbation.Footnote 20 For each scenario, the triangles labeled “Pseudo-Inferred Order” denote the actual results when applying the ordering deemed best according to the pseudo preference results, as described above. The figure shows that a large portion of the gain from carefully fixing the order of agents could be recovered if the planner is able to very accurately predict preferences, but how much can be gained could be very sensitive how good a prediction the planner makes.Footnote 21
5.2 Ordering Agents by Outcome Score Variance
We also explored an alternative strategy for identifying a priori (and hence without sacrificing strategy-proofness) an agent ordering that is likely to result in a favorable level of the top-3 metric. Rather than attempting to predict pseudo preferences, this strategy instead utilizes the families’ outcome scores. Specifically, for each family the variance of outcome scores across locations can be computed, and then agents can be ordered according to their variances. We propose ordering the agents in increasing variance (from lowest variance to highest variance). The intuition for this proposal is the following. In making assignments, the
![]() $\bar g$
-constrained priority mechanism is faced with the trade-off between sending agents to their preferred location and sending them to a location that will enable the
$\bar g$
-constrained priority mechanism is faced with the trade-off between sending agents to their preferred location and sending them to a location that will enable the
![]() $\bar g$
constraint to be met. For each agent, the extent to which this particular trade-off can bite depends to some degree on the variance of their outcome scores across locations. In the extreme case, there is no trade-off for an agent whose outcome score is identical across locations: no matter where they are sent, their assignment will have an equivalent implication for the
$\bar g$
constraint to be met. For each agent, the extent to which this particular trade-off can bite depends to some degree on the variance of their outcome scores across locations. In the extreme case, there is no trade-off for an agent whose outcome score is identical across locations: no matter where they are sent, their assignment will have an equivalent implication for the
![]() $\bar g$
constraint. However, for agents whose outcome score variance is very high, the extent to which their assignment can work in favor of or against the
$\bar g$
constraint. However, for agents whose outcome score variance is very high, the extent to which their assignment can work in favor of or against the
![]() $\bar g$
constraint varies greatly across locations. In other words, the high-variance agents’ assignments offer opportunity to create buffer for the
$\bar g$
constraint varies greatly across locations. In other words, the high-variance agents’ assignments offer opportunity to create buffer for the
![]() $\bar g$
constraint, whereas the low-variance agents’ assignments do not. Therefore, assigning low-variance agents earlier ensures that such units are more likely to be assigned to a highly preferred location without occurring at the expense of excessively cutting into the
$\bar g$
constraint, whereas the low-variance agents’ assignments do not. Therefore, assigning low-variance agents earlier ensures that such units are more likely to be assigned to a highly preferred location without occurring at the expense of excessively cutting into the
![]() $\bar g$
constraint.Footnote
22
$\bar g$
constraint.Footnote
22
Figure 7 shows the results of applying this increasing-variance ordering strategy (left panels) as well as the opposite decreasing-variance ordering for illustrative purposes (right panels). The components labeled “Many Orders” display the results from the same 100 random orderings as in Figure 6, with the black dots corresponding to the average across the 100 orderings and the intervals denoting the maximum and minimum results obtained across the 100 orderings. The components labeled “Variance-Based Order” display the results when applying the mechanism to the families put in the proposed increasing-variance order (left panels), or in the decreasing-variance order (right panels). The figures show that when agents are ordered by increasing outcome score variance, a substantial share of the gain from fixing the order of agents can be recovered. It also depicts what we expect would happen when agents are ordered by decreasing outcome score variance, which is that welfare measured by the top-3 metric is generally worse than under the typical random ordering.

Figure 7 Results from applying our
![]() $\bar g$
-constrained priority mechanism to 100 random orderings of a random sample of 100 families from the 2016 Q3 refugee data, along with outcome score variance-based orderings. The black dots correspond to the average results across the 100 orderings, and the intervals denote the maximum and minimum results obtained across the 100 orderings. The triangles (labeled “Variance-Based Order”) denote the results when employing orderings based on the families’ outcome score variances across locations, with families ordered by increasing variance on the left and decreasing variance on the right. Upper panel shows the average probability that an agent was assigned to one of its top-three locations. Lower panel shows the realized average outcome score.
$\bar g$
-constrained priority mechanism to 100 random orderings of a random sample of 100 families from the 2016 Q3 refugee data, along with outcome score variance-based orderings. The black dots correspond to the average results across the 100 orderings, and the intervals denote the maximum and minimum results obtained across the 100 orderings. The triangles (labeled “Variance-Based Order”) denote the results when employing orderings based on the families’ outcome score variances across locations, with families ordered by increasing variance on the left and decreasing variance on the right. Upper panel shows the average probability that an agent was assigned to one of its top-three locations. Lower panel shows the realized average outcome score.
![]() $N=100$
.
$N=100$
.
5.3 Overview
One property of the increasing outcome variance ordering approach is that it does not rely on historical (or any other) data to predict the preferences of agents. Another desirable property of this approach relates to fairness/distributive considerations: the agents that cannot gain much by way of their outcome score through different assignments can be prioritized to achieve gains in terms of their preferences, and those agents that have a lot to gain by way of outcome scores could enjoy such gains even if they do not get one of their top preferences. A concern with fixing the order of agents using either of these techniques, however, is that it may unintentionally though systematically put agents of particular backgrounds higher or lower in the priority order, a form of potential disparate impact that may not be desirable to the planner. In choosing the order of agents, one might want to incorporate additional constraints to overcome part of the bias that may be implicit in these techniques. More theoretical work will be necessary to evaluate how workable these and other approaches of using data and machine-learning techniques to determine the order of agents will be in various applications.
6 Other Mechanisms
As we have shown, the priority mechanism is a mechanism for which we can add a welfare constraint without compromising important properties such as strategy-proofness and (constrained) efficiency. One could ask whether we can amend other existing mechanisms to take into account the same constraint while retaining their desirable properties.
6.1 Top Trading Cycles
One candidate for an alternative mechanism, among matching mechanisms with one-sided preferences, is Gale’s TTC mechanism (Shapley and Scarf Reference Shapley and Scarf1974; Roth Reference Roth1982), which has already been employed in previous proposals for refugee matching (Delacrétaz et al. Reference Delacrétaz, Kominers and Teytelboym2016). However, adding a planner’s
![]() $\bar g$
constraint to this mechanism while retaining the feature that it is strategy-proof and constrained efficient is not straightforward.
$\bar g$
constraint to this mechanism while retaining the feature that it is strategy-proof and constrained efficient is not straightforward.
Consider, for example, the simple adjustment of this mechanism that begins by provisionally assigning agents to locations to maximize the planner’s objective and removes cycles until the planner’s welfare measure falls below the threshold, at which point it stops and everyone that is unassigned receives the assignment that they currently provisionally have. The following three person-three location example depicted in Figure 8 shows that this mechanism is not strategy-proof. The agents are
![]() $1, 2,$
and
$1, 2,$
and
![]() $3$
, and the locations are A, B, and C.
$3$
, and the locations are A, B, and C.

Figure 8 Three person-three location example showing violation of strategy-proofness when adding a planner’s
![]() $\bar g$
constraint to TTC mechanism.
$\bar g$
constraint to TTC mechanism.
To maximize the average outcomes score, agent 1 is provisionally assigned to A, 2 to B, and 3 to C. Preferences over locations are given on the left. In the middle, we have the values of
![]() $g_i(l)$
. Under truthful reporting, agent 1 points to B, and 2 and 3 point to A. The only cycle is between
$g_i(l)$
. Under truthful reporting, agent 1 points to B, and 2 and 3 point to A. The only cycle is between
![]() $1$
and
$1$
and
![]() $2$
. However, if the planner’s threshold
$2$
. However, if the planner’s threshold
![]() $\bar g$
is set to 0.5, then swapping 1 and 2’s locations guarantees an average outcome score below this threshold. The algorithm would terminate with the outcome maximizing assignment being assigned. However, agent 1 could do better by misreporting and pointing to C instead. In this case, the assignment would be 1 to C, 2 to B, and 3 to A, which gives an average outcome score above the threshold.
$\bar g$
is set to 0.5, then swapping 1 and 2’s locations guarantees an average outcome score below this threshold. The algorithm would terminate with the outcome maximizing assignment being assigned. However, agent 1 could do better by misreporting and pointing to C instead. In this case, the assignment would be 1 to C, 2 to B, and 3 to A, which gives an average outcome score above the threshold.
Thus, while it may be possible to incorporate an outcome constraint into the TTC mechanism that preserves strategy-proofness and constrained efficiency, it appears that there is no straightforward way to do so. For the priority mechanism, however, incorporating this constraint is both straightforward and computationally tractable.
6.2 Two-Sided Mechanisms
Finally, we could also consider matching mechanisms with two-sided preferences, such as the deferred acceptance mechanism (Gale and Shapley Reference Gale and Shapley1962), where we incorporate the planner’s welfare objective into the preferences for the locations. Here, there are at least two possibilities. First, we could assume that locations care about maximizing the planner’s welfare score, along with other considerations; that is, we allow the locations to express their genuine preferences. At least for the refugee assignment application, this appears to be politically challenging, partly because policymakers are concerned that this could result in political problems, where some locations might discriminate against refugees from certain groups/nationalities. The second possibility is we assume that each location simply wants to maximize the average outcome score among agents assigned to it. This creates competition among locations. Again, at least in the refugee assignment application, it is not clear why the planner (national government) would want to allow this—i.e., it is not clear what this assignment mechanism would achieve that serial priority does not, given the objectives of the planner.
7 Conclusion
We have proposed an assignment mechanism for contexts where there is a social planner/designer with their own welfare objective. Our mechanism strikes a compromise between maximizing the planner’s objective and conducting the assignment solely on the basis of the agents’ preferences. The mechanism is strategy-proof, constrained efficient, and does not require agents to rank all locations. In real-world implementations of our mechanism, a planner could either fix a feasible value of
![]() $\bar g$
in advance or review the projected results along a sequence of
$\bar g$
in advance or review the projected results along a sequence of
![]() $\bar g$
values (as in Figures 3 and 5) and choose the final preferred assignment according to their own criteria.
$\bar g$
values (as in Figures 3 and 5) and choose the final preferred assignment according to their own criteria.
We applied our mechanism to refugee assignment and school choice data to demonstrate how it could be implemented. Refugee matching has become a prominent policy innovation proposed to help facilitate the successful integration of refugees into host countries’ economies and societies. However, there is disagreement over whether integration is best served by matching on refugee preferences or expected integration outcomes. Our study highlights the value for governments to collect preference information from refugees to provide them with agency and improve allocations by harnessing the value of private information they possess over which locations work best for them. In addition, our mechanism is applicable to other domains that involve the assignment of agents to different types of locations (or more generally speaking, one-to-one and many-to-one bipartite matching problems). As a second example, we apply our mechanism to the assignment of kindergarteners to schools. School choice has been a longstanding application of market design, and our illustration demonstrates how our mechanism can be applied to this canonical setting.
In addition, our investigation resulted in interesting new theoretical insights. First, we discovered that the priority mechanism appears to be unique in the sense that our outcome constraint can be incorporated into it in a straightforward manner without sacrificing the important properties of strategy-proofness, efficiency, and computational tractability. In contrast, the simple modifications of the TTC that we considered to incorporate an outcome constraint did not retain strategy-proofness and/or computational tractability. Future research might consider other modifications that retain these properties. Second, we also discovered that not all of the canonical properties of the priority mechanism are inherited by our constrained version. Namely, the
![]() $\bar g$
-constrained priority mechanism does not characterize the full set of constrained efficient assignments.
$\bar g$
-constrained priority mechanism does not characterize the full set of constrained efficient assignments.
These applications of our mechanism provide examples of how predictive analytics from machine learning can be fruitfully combined with the preference-based allocation schemes common in market design. The marriage of these two approaches can provide a powerful tool to improve allocations in a way that incorporates information about what people want while harnessing the statistical learnings from the historical data about what would be the best options. Given the heterogeneity in information levels and the richness of historical data on outcomes, we envision that such a combined approach could lead to better allocations in a variety of settings compared to schemes that rely only on preferences or only on expected outcomes.
Acknowledgments
We acknowledge funding from the Rockefeller Foundation, Schmidt Futures, and the 2018 HAI seed grant program from the Stanford AI Lab, Stanford School of Medicine, and Stanford Graduate School of Business. The funders had no role in the data collection, analysis, decision to publish, or preparation of the manuscript. We thank the Lutheran Immigration and Refugee Service for access to data and guidance. We are grateful to Fuhito Kojima and Shunya Noda for help and guidance.
Data Availability Statement
Replication code for this article has been published in Code Ocean, a computational reproducibility platform that enables users to run the code, and can be viewed interactively at Acharya et al. (Reference Acharya, Bansak and Hainmueller2020a) or https://doi.org/10.24433/CO.3735899.v1. A preservation copy of the same code and data can also be accessed via Harvard Dataverse at Acharya et al. (Reference Acharya, Bansak and Hainmueller2020b) or https://doi.org/10.7910/DVN/ZEV0WX. The U.S. refugee data were provided to us under a collaboration research agreement with the Lutheran Immigration and Refugee Service (LIRS). This agreement requires that we do not transfer or disclose the data. Researchers interested in the data can contact LIRS at 700 Light Street, Baltimore, Maryland 21230, lirs@lirs.org. We declare that we have no competing interests.
Supplementary Material
For supplementary material accompanying this paper, please visit https://doi.org/10.1017/pan.2020.48.