1 Problem: Subpopulation Estimation with Irregular Data
Social scientists are often interested in how populations evolve over time. Estimating the composition of populations is a central concern of demography as well as a frequent target of ecological inference (EI). One common use of population estimates is as targets for weights designed to make samples more representative of the population. Survey researchers, for example, often poststratify poll samples so that the joint distribution of certain variables matches the target population. Constructing such multivariate population targets is straightforward when data on variables’ joint distribution can be derived from a single authoritative source, such as the Integrated Public Use Microdata Series (IPUMS) of anonymized samples of individual U.S. Census records (Ruggles et al. Reference Ruggles, Genadek, Goeken, Grover and Sobek2017). As long as the population data are observed in consistent form across time, it is also simple to make these population targets dynamic by interpolating between decennial IPUMS samples (e.g., Enns and Koch Reference Enns and Koch2013).
Frequently, however, data on population distributions must be compiled from multiple sources, which may exhibit inconsistencies due to sampling or measurement error. Moreover, the structure of population datasets or the variables they include often differ across time periods. Faced with such barriers to simple interpolation, scholars typically either use time-invariant population targets—which is obviously problematic for studies that span periods of substantial demographic change—or confine their attention to the few variables whose joint distribution is observed in consistent form across time (cf. Leeman and Wasserfallen Reference Leeman and Wasserfallen2017).
As an alternative, we develop a Bayesian framework for estimating population cell proportions over time, conditional on all available population data. The data may consist of marginal or joint distributions, be observed irregularly over time, and come from multiple noisy or inconsistent datasets. Extending the dynamic EI model of Quinn (Reference Quinn2004), our approach uses a Dirichlet random walk to allow past and future as well as contemporary data to inform the cell estimates for a given year. We motivate this model with the example of estimating phone ownership by race and region and implement it in a new R package, estsubpop (Caughey and Wang Reference Caughey and Wang2018a).
2 Motivation: Phone Ownership by Race and Region
As motivation, consider the challenge faced by Berinsky et al. (Reference Berinsky, Powell, Schickler and Yohai2011), who constructed survey weights for quota-sampled opinion polls fielded between 1936 and 1945. To ameliorate the sampling biases of the polls, the authors sought to poststratify the samples by region, race, and indicators of class status. But because poststratification (a.k.a. cell weighting) requires knowledge of the weighting variables’ joint distribution in the population, these authors could not poststratify on variables for which only marginal distributions were available, such as phone ownership. They were thus forced to choose to either drop phone ownership as a weighting variable or abandon poststratification in favor of raking weights, which match variables’ marginal but not joint distributions.Footnote 1
Table 1. Phone ownership by race by region in 1940. Unobserved cell proportions are represented by
![]() $\unicode[STIX]{x1D70B}$
and observed marginal proportions by
$\unicode[STIX]{x1D70B}$
and observed marginal proportions by
![]() $p$
. Subscripts indicate the presence (uppercase) or absence (lowercase) of the three attributes.
$p$
. Subscripts indicate the presence (uppercase) or absence (lowercase) of the three attributes.

Table 1 illustrates the structure of the problem Berinsky et al. faced, using data from 1940. It presents a
![]() $2\times 2\times 2$
array of cells defined by the binary variables South, Black, and Phone. Cells’ population proportions are represented by
$2\times 2\times 2$
array of cells defined by the binary variables South, Black, and Phone. Cells’ population proportions are represented by
![]() $\unicode[STIX]{x1D70B}$
, whose subscripts indicate the presence (uppercase) or absence (lowercase) of the three attributes. If these cell proportions were known, they could be used to create poststratification weights by dividing them by the cells’ corresponding proportions in the sample. But data on the joint distribution of these three variables is not available until the 1960 IPUMS, when phone-ownership rates were much higher than in 1936–45. All that is available in the 1936–45 period is information on the marginal distributions of Phone and Black within each region.Footnote
2
These observed marginal proportions are represented by
$\unicode[STIX]{x1D70B}$
, whose subscripts indicate the presence (uppercase) or absence (lowercase) of the three attributes. If these cell proportions were known, they could be used to create poststratification weights by dividing them by the cells’ corresponding proportions in the sample. But data on the joint distribution of these three variables is not available until the 1960 IPUMS, when phone-ownership rates were much higher than in 1936–45. All that is available in the 1936–45 period is information on the marginal distributions of Phone and Black within each region.Footnote
2
These observed marginal proportions are represented by
![]() $p$
.
$p$
.
If race and phone ownership were independent within region, the cell proportions could be estimated by multiplying the corresponding marginal proportions. Under this assumption, the phone-ownership rate in the South in 1940 would be naively estimated to be 19% for both blacks and whites. Unfortunately, this assumption is highly implausible, for phone ownership was almost certainly much more common among whites. This racial disparity is clear in the 1960 IPUMS, which reports a phone-ownership rate of 70% for Southern whites versus 39% for Southern blacks. The problem, then, is how to formally incorporate the 1960 information on the joint distribution of South, Black, and Phone into our cell estimates two decades earlier.
3 Related Problems and Methods
The problem illustrated in the previous section is closely related to classic problems in EI, such as the oft-studied example of voter registration by race. (In EI, the quantities of interest are often defined as conditional rates rather than cell proportions, but the latter are a function of the former; King Reference King1997, 29–31.)Footnote
3
EI is unreliable without supplementary data or prior information, and Bayesian models offer a convenient way of incorporating additional information. Most relevantly, Quinn (Reference Quinn2004) develops a dynamic EI model that shrinks estimates across time periods, which he notes are a powerful source of such information when data are temporally dependent. Quinn’s model, however, is designed for situations where the margins of the same
![]() $2\times 2$
table are observed in the same form in each time period. By contrast, we are interested in applications where there may be multiple (possibly inconsistent) data sources available in a given year, and the structure and content of the data may differ across years. We therefore augment Quinn’s approach with ideas borrowed from demography (e.g., Bryant and Graham Reference Bryant and Graham2013), specifically the idea of combining (1) multiple observation models for different data sources; (2) a “demographic account” that encodes the logical relationships among different population quantities; and (3) a transition model for change in population parameters across time periods.Footnote
4
$2\times 2$
table are observed in the same form in each time period. By contrast, we are interested in applications where there may be multiple (possibly inconsistent) data sources available in a given year, and the structure and content of the data may differ across years. We therefore augment Quinn’s approach with ideas borrowed from demography (e.g., Bryant and Graham Reference Bryant and Graham2013), specifically the idea of combining (1) multiple observation models for different data sources; (2) a “demographic account” that encodes the logical relationships among different population quantities; and (3) a transition model for change in population parameters across time periods.Footnote
4
4 A Bayesian Model for Dynamic Population Estimation
Estimating the joint population distribution of
![]() $V$
nonnested categorical variables is equivalent to estimating the population proportions of
$V$
nonnested categorical variables is equivalent to estimating the population proportions of
![]() $C=\prod _{v}^{V}L_{v}$
cells, where
$C=\prod _{v}^{V}L_{v}$
cells, where
![]() $L_{v}$
indicates the number of possible values that variable
$L_{v}$
indicates the number of possible values that variable
![]() $v$
can take. Let
$v$
can take. Let
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{t}=(\unicode[STIX]{x1D70B}_{t1},\ldots \unicode[STIX]{x1D70B}_{tc},\ldots ,\unicode[STIX]{x1D70B}_{tC})^{\prime }$
denote the simplex of cell proportions in period
$\boldsymbol{\unicode[STIX]{x1D70B}}_{t}=(\unicode[STIX]{x1D70B}_{t1},\ldots \unicode[STIX]{x1D70B}_{tc},\ldots ,\unicode[STIX]{x1D70B}_{tC})^{\prime }$
denote the simplex of cell proportions in period
![]() $t\in \{1\ldots T\}$
. In each period, population data are available on the joint distribution of
$t\in \{1\ldots T\}$
. In each period, population data are available on the joint distribution of
![]() $M_{t}\geqslant 0$
subsets of the
$M_{t}\geqslant 0$
subsets of the
![]() $V$
variables. Each variable subset
$V$
variables. Each variable subset
![]() $m\in \{1\cdots M_{t}\}$
contains
$m\in \{1\cdots M_{t}\}$
contains
![]() $V_{tm}\leqslant V$
variables, whose levels define
$V_{tm}\leqslant V$
variables, whose levels define
![]() $G_{tm}=\prod _{w}^{V_{tm}}L_{w}$
groups, each composed of
$G_{tm}=\prod _{w}^{V_{tm}}L_{w}$
groups, each composed of
![]() $H_{tmg}\geqslant 1$
cells. The population data for each variable subset
$H_{tmg}\geqslant 1$
cells. The population data for each variable subset
![]() $m$
in period
$m$
in period
![]() $t$
consist of the simplex
$t$
consist of the simplex
![]() $\boldsymbol{p}_{tm}=(p_{tm1},\ldots p_{tmg},\ldots ,p_{tmG_{tm}})^{\prime }$
. Each group proportion
$\boldsymbol{p}_{tm}=(p_{tm1},\ldots p_{tmg},\ldots ,p_{tmG_{tm}})^{\prime }$
. Each group proportion
![]() $p_{tmg}$
is an estimate of group
$p_{tmg}$
is an estimate of group
![]() $g$
’s true population proportion
$g$
’s true population proportion
![]() $\unicode[STIX]{x1D719}_{tmg}$
, the sum of the proportions
$\unicode[STIX]{x1D719}_{tmg}$
, the sum of the proportions
![]() $\unicode[STIX]{x1D70B}_{tc}$
of the cells that compose group
$\unicode[STIX]{x1D70B}_{tc}$
of the cells that compose group
![]() $g$
.
$g$
.
For intuition, consider the problem of using the 1960 IPUMS and the 1940 data in Table 1 to estimate phone ownership by race and region between 1940 and 1960. This example involves
![]() $V=3$
auxiliary variables (South, Black, and Phone), each with
$V=3$
auxiliary variables (South, Black, and Phone), each with
![]() $L_{v}=2$
levels. Of interest are the population proportions
$L_{v}=2$
levels. Of interest are the population proportions
![]() $\unicode[STIX]{x1D70B}_{tc}$
of
$\unicode[STIX]{x1D70B}_{tc}$
of
![]() $C=2\,\times \,2\,\times \,2=8$
cells in each of
$C=2\,\times \,2\,\times \,2=8$
cells in each of
![]() $T=21$
years. In 1940 (
$T=21$
years. In 1940 (
![]() $t=1$
), data on the joint distribution of
$t=1$
), data on the joint distribution of
![]() $M_{1}=2$
variable subsets are available:
$M_{1}=2$
variable subsets are available:
![]() $\{\mathit{South},\mathit{Black}\}$
and
$\{\mathit{South},\mathit{Black}\}$
and
![]() $\{\mathit{South},\mathit{Phone}\}$
. For each variable subset
$\{\mathit{South},\mathit{Phone}\}$
. For each variable subset
![]() $m$
,
$m$
,
![]() $V_{1,m}=2$
,
$V_{1,m}=2$
,
![]() $G_{1,m}=4$
, and
$G_{1,m}=4$
, and
![]() $H_{1,mg}=2\;\forall g$
. We observe
$H_{1,mg}=2\;\forall g$
. We observe
![]() $M_{1}=2$
vectors of group proportions
$M_{1}=2$
vectors of group proportions
![]() $\boldsymbol{p}_{1,m}$
, which are estimates of
$\boldsymbol{p}_{1,m}$
, which are estimates of
![]() $\boldsymbol{\unicode[STIX]{x1D719}}_{1,m}$
and which correspond to the marginal proportions in Table 1 (with different notation). In 1960 (
$\boldsymbol{\unicode[STIX]{x1D719}}_{1,m}$
and which correspond to the marginal proportions in Table 1 (with different notation). In 1960 (
![]() $t=21$
),
$t=21$
),
![]() $M_{21}=1$
variable subset is available:
$M_{21}=1$
variable subset is available:
![]() $\{\mathit{South},\mathit{Black},\mathit{Phone}\}$
. For this subset,
$\{\mathit{South},\mathit{Black},\mathit{Phone}\}$
. For this subset,
![]() $V_{21,m}=3$
,
$V_{21,m}=3$
,
![]() $G_{21,m}=8$
, and
$G_{21,m}=8$
, and
![]() $H_{21,mg}=1\;\forall g$
. No data are available for years between 1940 and 1960, so
$H_{21,mg}=1\;\forall g$
. No data are available for years between 1940 and 1960, so
![]() $M_{t}=0\;\forall t\notin \{1,21\}$
.
$M_{t}=0\;\forall t\notin \{1,21\}$
.
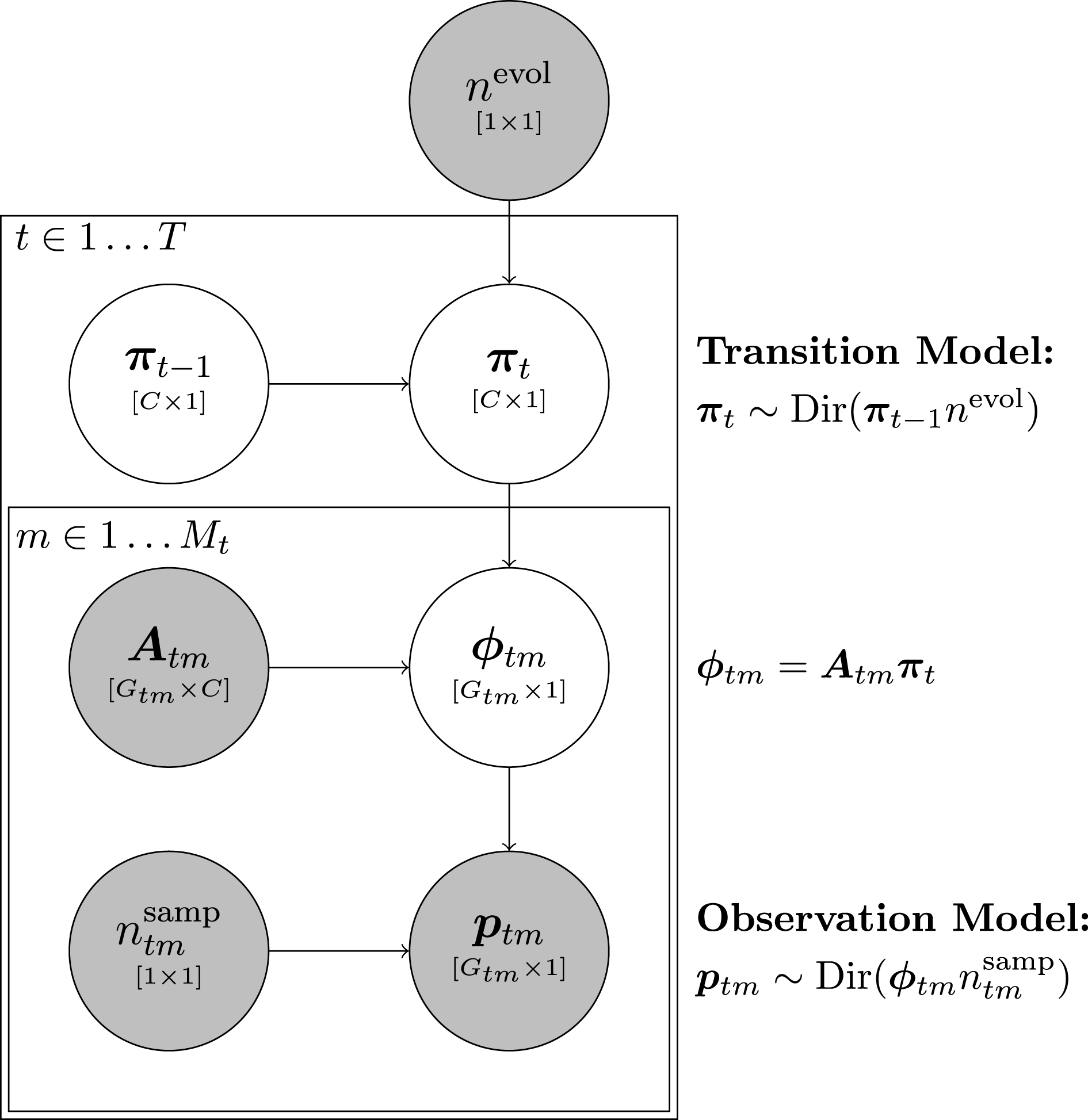
Figure 1. Plate diagram of the dynamic EI model. Shaded nodes indicate variables that are observed or set by the analyst.
Our goal is to use the observed group proportions
![]() $\boldsymbol{p}_{tm}$
to make inferences about the true cell proportions
$\boldsymbol{p}_{tm}$
to make inferences about the true cell proportions
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{t}$
. We do so with a Bayesian model that combines two submodels: an observation model linking
$\boldsymbol{\unicode[STIX]{x1D70B}}_{t}$
. We do so with a Bayesian model that combines two submodels: an observation model linking
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{t}$
(via
$\boldsymbol{\unicode[STIX]{x1D70B}}_{t}$
(via
![]() $\boldsymbol{\unicode[STIX]{x1D719}}_{tm}$
) to the data
$\boldsymbol{\unicode[STIX]{x1D719}}_{tm}$
) to the data
![]() $\boldsymbol{p}_{tm}$
and a transition model specifying how
$\boldsymbol{p}_{tm}$
and a transition model specifying how
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{t}$
evolves over time (see Figure 1 for an overview).Footnote
5
The observation model allows for measurement error in the observed group proportions
$\boldsymbol{\unicode[STIX]{x1D70B}}_{t}$
evolves over time (see Figure 1 for an overview).Footnote
5
The observation model allows for measurement error in the observed group proportions
![]() $\boldsymbol{p}_{tm}$
relative to the true proportions
$\boldsymbol{p}_{tm}$
relative to the true proportions
![]() $\boldsymbol{\unicode[STIX]{x1D719}}_{tm}$
. We represent this stochastic relationship between
$\boldsymbol{\unicode[STIX]{x1D719}}_{tm}$
. We represent this stochastic relationship between
![]() $\boldsymbol{p}_{tm}$
and
$\boldsymbol{p}_{tm}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D719}}_{tm}$
using the Dirichlet distribution,
$\boldsymbol{\unicode[STIX]{x1D719}}_{tm}$
using the Dirichlet distribution,
Under this model, the expected value of
![]() $p_{tmg}$
is
$p_{tmg}$
is
![]() $\unicode[STIX]{x1D719}_{tmg}$
. The precision of the sampling distribution is determined by
$\unicode[STIX]{x1D719}_{tmg}$
. The precision of the sampling distribution is determined by
![]() $n_{tm}^{\text{samp}}$
, which is specified by the analyst (e.g., based on the actual sample size of the data source for
$n_{tm}^{\text{samp}}$
, which is specified by the analyst (e.g., based on the actual sample size of the data source for
![]() $\boldsymbol{p}_{tm}$
).Footnote
6
$\boldsymbol{p}_{tm}$
).Footnote
6
Each group proportion
![]() $\unicode[STIX]{x1D719}_{tmg}$
is the sum of the proportions of the
$\unicode[STIX]{x1D719}_{tmg}$
is the sum of the proportions of the
![]() $H_{tmg}$
cells that compose it. The relationship between
$H_{tmg}$
cells that compose it. The relationship between
![]() $\boldsymbol{\unicode[STIX]{x1D719}}_{tm}$
and
$\boldsymbol{\unicode[STIX]{x1D719}}_{tm}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{t}$
is thus compactly described by the equation
$\boldsymbol{\unicode[STIX]{x1D70B}}_{t}$
is thus compactly described by the equation
where
![]() $\boldsymbol{A}_{tm}$
is a
$\boldsymbol{A}_{tm}$
is a
![]() $G_{tm}\times C$
indicator matrix in which a 1 in row
$G_{tm}\times C$
indicator matrix in which a 1 in row
![]() $g$
and column
$g$
and column
![]() $c$
indicates that group
$c$
indicates that group
![]() $g$
contains cell
$g$
contains cell
![]() $c$
. In Table 1, for example, the
$c$
. In Table 1, for example, the
![]() $M_{1940}=2$
vectors of observed (estimated) group proportions are
$M_{1940}=2$
vectors of observed (estimated) group proportions are
and the corresponding unobserved (true) proportions are
 $$\begin{eqnarray}\displaystyle \boldsymbol{\unicode[STIX]{x1D719}}_{1940,\mathit{South}\times \mathit{Black}} & = & \displaystyle (\unicode[STIX]{x1D70B}_{\text{SBP}}+\unicode[STIX]{x1D70B}_{\text{SBp}},\unicode[STIX]{x1D70B}_{\text{SbP}}+\unicode[STIX]{x1D70B}_{\text{Sbp}},\unicode[STIX]{x1D70B}_{\text{sBP}}+\unicode[STIX]{x1D70B}_{\text{sBp}},\unicode[STIX]{x1D70B}_{\text{sbP}}+\unicode[STIX]{x1D70B}_{\text{sbp}})\nonumber\\ \displaystyle & = & \displaystyle \boldsymbol{A}_{1940,\mathit{South}\times \mathit{Black}}\boldsymbol{\unicode[STIX]{x1D70B}}_{1940}\nonumber\\ \displaystyle \boldsymbol{\unicode[STIX]{x1D719}}_{1940,\mathit{South}\times \mathit{Phone}} & = & \displaystyle (\unicode[STIX]{x1D70B}_{\text{SBP}}+\unicode[STIX]{x1D70B}_{\text{SbP}},\unicode[STIX]{x1D70B}_{\text{SBp}}+\unicode[STIX]{x1D70B}_{\text{Sbp}},\unicode[STIX]{x1D70B}_{\text{sBP}}+\unicode[STIX]{x1D70B}_{\text{sbP}},\unicode[STIX]{x1D70B}_{\text{sBp}}+\unicode[STIX]{x1D70B}_{\text{sbp}})\nonumber\\ \displaystyle & = & \displaystyle \boldsymbol{A}_{1940,\mathit{South}\times \mathit{Phone}}\boldsymbol{\unicode[STIX]{x1D70B}}_{1940}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{\unicode[STIX]{x1D719}}_{1940,\mathit{South}\times \mathit{Black}} & = & \displaystyle (\unicode[STIX]{x1D70B}_{\text{SBP}}+\unicode[STIX]{x1D70B}_{\text{SBp}},\unicode[STIX]{x1D70B}_{\text{SbP}}+\unicode[STIX]{x1D70B}_{\text{Sbp}},\unicode[STIX]{x1D70B}_{\text{sBP}}+\unicode[STIX]{x1D70B}_{\text{sBp}},\unicode[STIX]{x1D70B}_{\text{sbP}}+\unicode[STIX]{x1D70B}_{\text{sbp}})\nonumber\\ \displaystyle & = & \displaystyle \boldsymbol{A}_{1940,\mathit{South}\times \mathit{Black}}\boldsymbol{\unicode[STIX]{x1D70B}}_{1940}\nonumber\\ \displaystyle \boldsymbol{\unicode[STIX]{x1D719}}_{1940,\mathit{South}\times \mathit{Phone}} & = & \displaystyle (\unicode[STIX]{x1D70B}_{\text{SBP}}+\unicode[STIX]{x1D70B}_{\text{SbP}},\unicode[STIX]{x1D70B}_{\text{SBp}}+\unicode[STIX]{x1D70B}_{\text{Sbp}},\unicode[STIX]{x1D70B}_{\text{sBP}}+\unicode[STIX]{x1D70B}_{\text{sbP}},\unicode[STIX]{x1D70B}_{\text{sBp}}+\unicode[STIX]{x1D70B}_{\text{sbp}})\nonumber\\ \displaystyle & = & \displaystyle \boldsymbol{A}_{1940,\mathit{South}\times \mathit{Phone}}\boldsymbol{\unicode[STIX]{x1D70B}}_{1940}.\nonumber\end{eqnarray}$$
The observed group proportions can be directly linked to the unobserved cell proportions by substituting (2) into (1), leading to the observation model
The model defined by (3) does not distinguish among cells in the same group
![]() $g$
, so without further information the posterior distributions over the cell proportions will be equal within groups. If there is only
$g$
, so without further information the posterior distributions over the cell proportions will be equal within groups. If there is only
![]() $M_{t}=1$
set of auxiliary variables, the posterior estimate of each cell proportion
$M_{t}=1$
set of auxiliary variables, the posterior estimate of each cell proportion
![]() $\unicode[STIX]{x1D70B}_{tc}$
in group
$\unicode[STIX]{x1D70B}_{tc}$
in group
![]() $g$
will converge to the maximum likelihood estimate
$g$
will converge to the maximum likelihood estimate
![]() $p_{tmg}/H_{tmg}$
, yielding weights identical to those that would be obtained with poststratification. If there are data on multiple sets of auxiliary variables, as in Table 1, then each of the
$p_{tmg}/H_{tmg}$
, yielding weights identical to those that would be obtained with poststratification. If there are data on multiple sets of auxiliary variables, as in Table 1, then each of the
![]() $M_{t}>1$
observation models will inform the cell estimates, yielding weights similar to those created by raking or calibration on the
$M_{t}>1$
observation models will inform the cell estimates, yielding weights similar to those created by raking or calibration on the
![]() $M_{t}$
vectors of marginal proportions
$M_{t}$
vectors of marginal proportions
![]() $\boldsymbol{p}_{tm}$
.
$\boldsymbol{p}_{tm}$
.
In general, however, there may be not only multiple sets of auxiliary variables available in a given year but also different sets across years. Data from other years can thus provide information distinguishing cells for which no individuating data are available in year
![]() $t$
. To pool this information across time periods, we model the temporal evolution of the proportion vector
$t$
. To pool this information across time periods, we model the temporal evolution of the proportion vector
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{t}$
using a Dirichlet transition model (cf. Grunwald, Raftery, and Guttorp Reference Grunwald, Raftery and Guttorp1993),
$\boldsymbol{\unicode[STIX]{x1D70B}}_{t}$
using a Dirichlet transition model (cf. Grunwald, Raftery, and Guttorp Reference Grunwald, Raftery and Guttorp1993),
where
![]() $\unicode[STIX]{x1D70B}_{t-1,c}$
is the expected value of
$\unicode[STIX]{x1D70B}_{t-1,c}$
is the expected value of
![]() $\unicode[STIX]{x1D70B}_{tc}$
.Footnote
7
In periods with no data,
$\unicode[STIX]{x1D70B}_{tc}$
.Footnote
7
In periods with no data,
![]() $\boldsymbol{\unicode[STIX]{x1D70B}}_{t}$
will be interpolated with values informed directly by the immediately adjacent periods and, indirectly, by all previous and subsequent estimates.
$\boldsymbol{\unicode[STIX]{x1D70B}}_{t}$
will be interpolated with values informed directly by the immediately adjacent periods and, indirectly, by all previous and subsequent estimates.
Since the variance of the Dirichlet is inversely proportional to the sample size, the hyperparameter
![]() $n^{\text{evol}}$
governs the degree of pooling across periods. It is possible either to set
$n^{\text{evol}}$
governs the degree of pooling across periods. It is possible either to set
![]() $n^{\text{evol}}$
exactly (as depicted in Figure 1) or to give it a hyperprior, but either way it should be specified with care because the degree of pooling over time can substantially affect inferences. In our application, we found that with a diffuse prior,
$n^{\text{evol}}$
exactly (as depicted in Figure 1) or to give it a hyperprior, but either way it should be specified with care because the degree of pooling over time can substantially affect inferences. In our application, we found that with a diffuse prior,
![]() $n^{\text{evol}}$
was usually estimated to be less than 2,000, which is too low to propagate much information across our three-decade period of interest.Footnote
8
We therefore recommend that analysts use substantive judgement to select a value or informative prior for
$n^{\text{evol}}$
was usually estimated to be less than 2,000, which is too low to propagate much information across our three-decade period of interest.Footnote
8
We therefore recommend that analysts use substantive judgement to select a value or informative prior for
![]() $n^{\text{evol}}$
. In general,
$n^{\text{evol}}$
. In general,
![]() $n^{\text{evol}}$
should be set large enough to propagate information across years without data, but not so large as to outweigh data when they are observed. One way to think through particular values of
$n^{\text{evol}}$
should be set large enough to propagate information across years without data, but not so large as to outweigh data when they are observed. One way to think through particular values of
![]() $n^{\text{evol}}$
is to reason backward from a “typical” yearly change. For instance, the expectation that a cell that currently constitutes half the population will change by a percentage point between years implies a choice of
$n^{\text{evol}}$
is to reason backward from a “typical” yearly change. For instance, the expectation that a cell that currently constitutes half the population will change by a percentage point between years implies a choice of
![]() $n^{\text{evol}}=0.5\times (1-0.5)/0.01^{2}=2\text{,}500$
. For an illustration of the consequences of different choices of
$n^{\text{evol}}=0.5\times (1-0.5)/0.01^{2}=2\text{,}500$
. For an illustration of the consequences of different choices of
![]() $n^{\text{evol}}$
, see Supplementary Appendix A.1.3.
$n^{\text{evol}}$
, see Supplementary Appendix A.1.3.
5 Validation
To validate our model, we examine how accurately it recovers the known cross-tabulation of South, Black, and Phone in the 1960, 1970, 1980, and 1990 IPUMS based on partial information about the joint distribution.Footnote 9 We compare estimates based on four data configurations:
(1) One-way marginal distributions in each year;
(2) Marginals in each year for
 $\mathit{Black}\times \mathit{South}$
and
$\mathit{Black}\times \mathit{South}$
and
 $\mathit{Phone}\times \mathit{South}$
but not
$\mathit{Phone}\times \mathit{South}$
but not
 $\mathit{Black}\times \mathit{Phone}$
;
$\mathit{Black}\times \mathit{Phone}$
;(3) Three-way crosstab in 1960 but otherwise the same two-way marginals as 2 above;
(4) Three-way crosstabs in all years.
Case 3 closely mirrors the data structure in our substantive application except that the 1960 crosstab data are used to inform estimates for future rather than past years. For all cases we set
![]() $\unicode[STIX]{x1D70B}_{0c}=1/8\;\forall c$
,
$\unicode[STIX]{x1D70B}_{0c}=1/8\;\forall c$
,
![]() $n^{\text{prior}}=8$
, and
$n^{\text{prior}}=8$
, and
![]() $n^{\text{evol}}=\exp (10)\approx 22\text{,}026$
.Footnote
10
We estimate the model in the Bayesian simulation program Stan (Stan Development Team 2018), as called from R by estsubpop.Footnote
11
$n^{\text{evol}}=\exp (10)\approx 22\text{,}026$
.Footnote
10
We estimate the model in the Bayesian simulation program Stan (Stan Development Team 2018), as called from R by estsubpop.Footnote
11
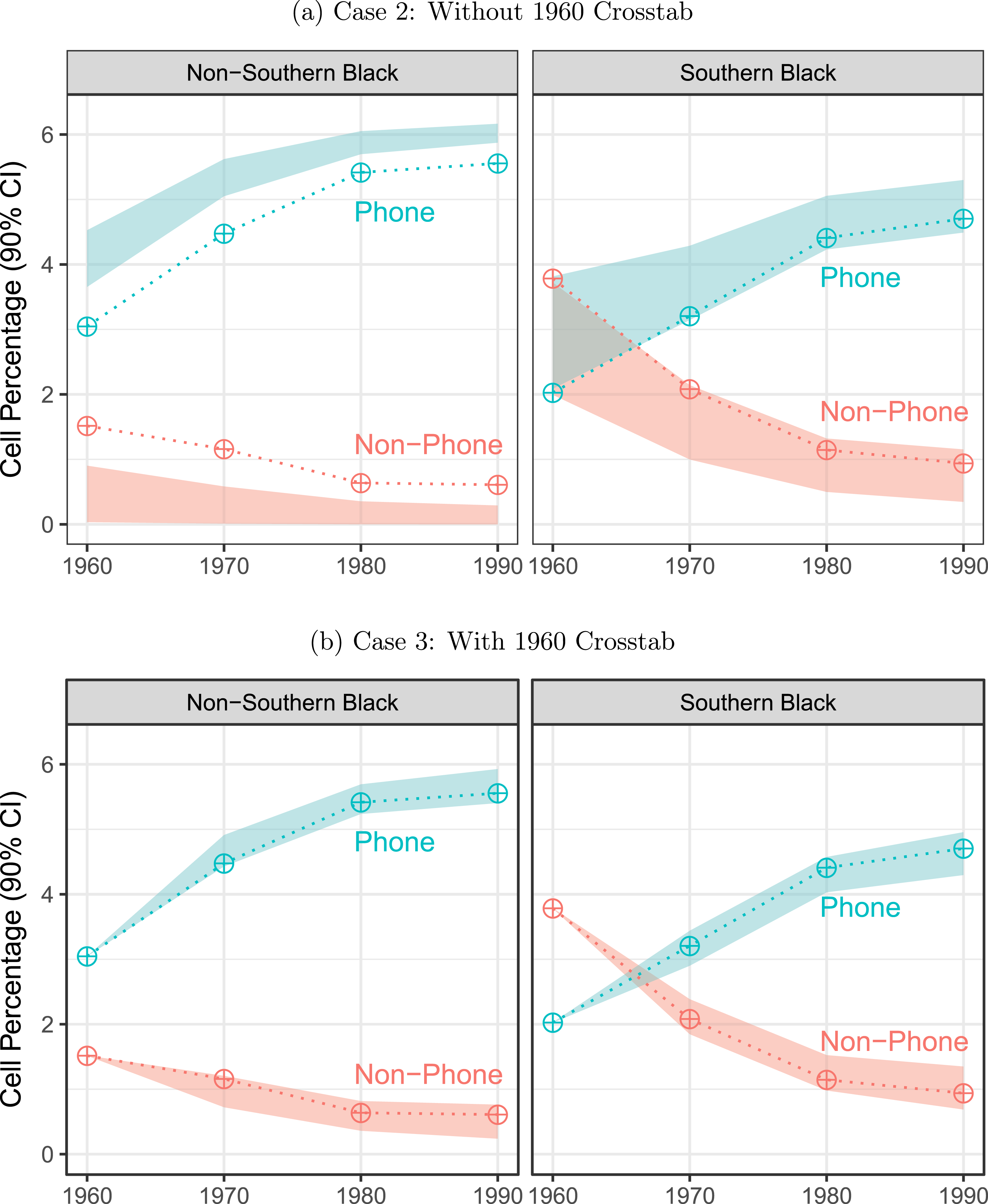
Figure 2. Cell estimates for Southern and non-Southern blacks, based on data with (bottom) and without (top) the full crosstab in 1960. Crosshairs and dotted lines indicate IPUMS targets. Shaded regions indicate 90% credible intervals.
Figure 2 plots the key comparison, case 3 (with 1960 crosstabs) versus case 2 (without), focusing the estimated population percentages of phone-owning and non-phone-owning blacks in each region. Despite sharing the same data as case 2 in 1970, 1980, and 1990, case 3’s credible intervals (CIs) track the true IPUMS targets in these years much more closely. This is due to 1960’s information on phone ownership by race, which is propagated forward in time. The performance of all four sets of estimates is formally compared in Figure 3. As one would hope, estimates based on the full joint distribution in every year (case 4) perform best in terms of root mean squared error (RMSE) and CI noncoverage.Footnote 12 However, the case 3 estimates (dotted line) are very accurate as well and clearly outperform cases 2 and 1. Not only are case 3’s RMSEs a tenth as large as case 2’s, but its CIs also do not exhibit false precision. In short, this simulation validates the usefulness of a model that can accommodate varying data structures over time, without which the crosstab data from 1960 could not be utilized.

Figure 3. Accuracy of estimates based on different data configurations. The middle and right panels respectively report the proportion of true cell proportions not covered by the 50% and 90% CIs.
6 Application
We now apply this approach to a more elaborate version of our running example, estimating the joint distribution of South, Black, and Phone in each year between 1930 and 1960. Table 2 details the population data we use to inform our estimates. While marginal data somewhat more frequent in this application than in the validation example, the key similarity is that data on full distribution are available only for 1960, well outside our main period of interest (1936–45).
As in Section 5, we set
![]() $\unicode[STIX]{x1D70B}_{0c}=1/8\;\forall c$
,
$\unicode[STIX]{x1D70B}_{0c}=1/8\;\forall c$
,
![]() $n^{\text{prior}}=8$
, and
$n^{\text{prior}}=8$
, and
![]() $n^{\text{evol}}=\exp (10)\approx 22\text{,}026$
(see Supplementary Appendix A.1.3 for a sensitivity analysis).Footnote
13
Estimating the model with these data generates
$n^{\text{evol}}=\exp (10)\approx 22\text{,}026$
(see Supplementary Appendix A.1.3 for a sensitivity analysis).Footnote
13
Estimating the model with these data generates
![]() $C=8$
estimated proportions in each of the
$C=8$
estimated proportions in each of the
![]() $T=31$
years. We transform these cell proportions into implied phone-ownership percentages by race and region and plot their posterior medians and 50% CIs in Figure 4. Notwithstanding the general growth in phone ownership after 1935, the ownership rate among blacks is always estimated to be lower than non-blacks in the same region. Note that because only a small percentage of non-Southerners in this period were African American, the ownership rate among non-Southern blacks is estimated much less precisely than that of the other three groups.
$T=31$
years. We transform these cell proportions into implied phone-ownership percentages by race and region and plot their posterior medians and 50% CIs in Figure 4. Notwithstanding the general growth in phone ownership after 1935, the ownership rate among blacks is always estimated to be lower than non-blacks in the same region. Note that because only a small percentage of non-Southerners in this period were African American, the ownership rate among non-Southern blacks is estimated much less precisely than that of the other three groups.
Table 2. Population data for example application.
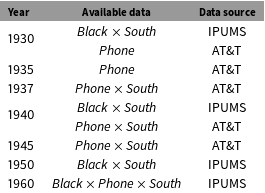
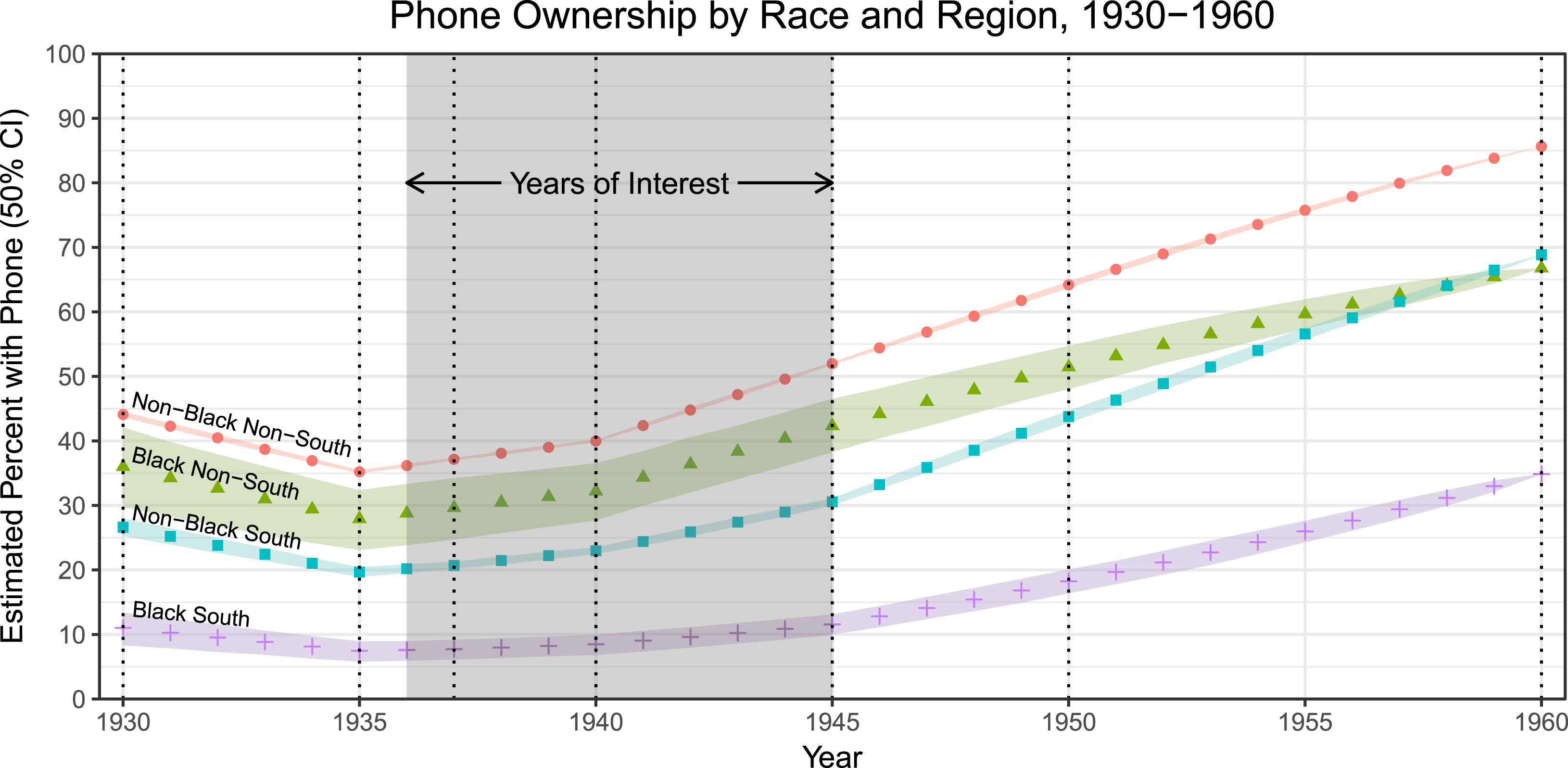
Figure 4. Phone ownership by race and region, 1930–60. Vertical dotted lines indicate years for which population data are available.
In addition to their substantive plausibility, the estimates are roughly consistent with other sources from this period. For example, a 1935–36 government study of consumer purchases found that non-black Southerners were 3.3 times more likely to own a phone than black Southerners, which is not far from our estimated ratio of around 2.8.Footnote 14 This convergence, combined with the analogous model’s accuracy in Section 5’s validation analysis, bolsters our confidence that our subpopulation estimates are much more accurate than if phone ownership and race were assumed to be independent.
7 Conclusion
The basic approach outlined above can be applied in a variety of empirical settings. Our original motivation was creating dynamic population targets for creating survey weights, and we have used the model to create dynamic population targets for as many as 2,302 demographic types defined by the cross-classification of six variables over three decades (Caughey and Wang Reference Caughey and Wang2014). In addition to survey weights, such population targets may be used for multilevel regression and poststratification (Park, Gelman, and Bafumi Reference Park, Gelman and Bafumi2004) or for generalizing causal effect estimates (Hartman et al. Reference Hartman, Grieve, Ramsahai and Sekhon2015). Moreover, as Section 6 showed, the same model can be used to estimate conditional rates—the traditional focus of EI—in settings where the data structure is too irregular for conventional EI models.
The model itself could be extended and improved in various ways. One area for improvement is computational efficiency, which can become a problem as the number of cells grows. For example, in order to obtain satisfactory estimates for over 2,000 cells, we had to let Stan run for several weeks. It is possible that this problem could be overcome with approximate inference such as variational Bayes, or perhaps by reparameterizing the model so as to ease the computational difficulty of estimating proportions very close to 0. One natural alternative parameterization would be the logistic-normal distribution in place of the Dirichlet (Cargnoni, Muller, and West Reference Cargnoni, Muller and West1997). In addition to possible computational benefits, the logistic normal would allow for more flexible patterns of dependence across cells than the Dirichlet, whose assumption of independence across components may be undesirable in some applications.
Supplementary material
For supplementary material accompanying this paper, please visithttps://doi.org/10.1017/pan.2019.4.







