1 Introduction
Political scientists are increasingly interested in using network analysis to understand how individuals, institutions, and states influence each other over time (Lazer et al. Reference Lazer, Brewer, Christakis, Fowler and King2009). Such work requires data on every connection each actor maintains with all other actors; these data are prohibitively costly to obtain when networks are large or change frequently. This cost is why existing time-series network analysis focuses on states at the year level (Dorussen and Ward Reference Dorussen and Ward2008; Oatley et al. Reference Oatley, Winecoff, Pennock and Danzman2013).
This paper introduces a statistic, neighbor cumulative indegree centrality (NCC), that allows for network time-series analysis of individuals at the daily level. NCC measures influence without data on every connection each actor maintains. Obviating the need for complete network data reduces research costs, allowing for daily network analysis of individuals. Moreover, NCC recovers an individual’s influence that would be observed if complete data were available, and it outperforms the other measure, indegree centrality, that is currently used with incomplete data.
NCC works best when the researcher can perform a breadth-first search—record all the connections for each individual being studied—and knows the number of connections each connection has. This situation is common for online social network data, as platforms such as Twitter and Instagram provide the number of connections each account has without the researcher having to manually download those connections. These data can also be obtained easily in surveys with a network component. For example, Karl-Dieter Opp and Christiane Gern surveyed participants in the 1989 Leipzig protests and asked if they had friends or co-workers who participated; if they had also asked respondents to rate those friends or co-workers on a popularity scale, the authors could have also determined if protestors are more likely to be influential in a network (high NCC) or not (low NCC) (Opp and Gern Reference Opp and Gern1993).
NCC is also favorable when a researcher faces resource constraints. It is common for rate limits to slow the amount of information that can be downloaded from digital sources or limited funding to restrict the amount of data that can be gathered via in-person enumeration. Since it does not require complete network data, NCC uses much less data than common measures of influence such as eigenvector, PageRank, or closeness centrality. Only in small or stable networks such as a classroom, bill co-sponsorship, offices, or country alliances, among others, are other influence measures preferable.
The NCC measure is demonstrated in the context of activists and the Arab Spring. The influence (NCC ranking) of 21 Bahraini and Egyptian Twitter accounts is tracked over a three-month month period, as is those accounts’ communication patterns. Models show that accounts which coordinate protests gain influence according to the NCC measure, while degree centrality influence suggests that the use of hashtags also matters. This result stands in contrast to work using hashtag analysis to suggest the periphery of social networks drives protest mobilization (Barberá et al. Reference Barberá, Wang, Bonneau, Jost, Nagler, Tucker and González-Bailón2015; Steinert-Threlkeld et al. Reference Steinert-Threlkeld, Mocanu, Vespignani and Fowler2015; Steinert-Threlkeld Reference Steinert-Threlkeld2017).
Section 2 explains longitudinal analysis with NCC. Section 3 explains why to prefer node rankings instead of raw centrality scores, NCC to indegree centrality, and under what situations NCC should be preferred to global centrality measures. Section 4 details a substantive application of the new measures: activism during the Arab Spring in Bahrain and Egypt. The main result of this analysis is that accounts that use more hashtags become more influential based on degree centrality but not NCC, while both measures show that accounts become more influential when their messages coordinate protest. Section 5 provides detail on other applications of longitudinal NCC measurement; these methods can be used for scholars interested in identifying hidden influentials as well as voter mobilization, among other areas. Section 6 concludes.
2 Network Centrality, Over Time
2.1 Network centrality with incomplete data
In network analyses, centrality refers to a set of statistics that attempt to measure which nodes are most influential, where the definition of influence varies according to the kind of network studied. (“Node” means the entity that forms the network under study. It could be an individual, a web page, an Internet router, an international organization, or a court case, for example. For the rest of this paper, “node” means individual, individual means node.) In this paper, Individual A is more influential than Individual B if the information he or she emits is seen by more people than that from Individual B. There are three main classes of centrality: betweenness, closeness, and degree-based. Each class of centrality measurement requires data on each node in the network (every website on the Internet, every student in a school, or every nation in a trade network, for example) and the connections between those nodes (every link between web pages, every friend of each student, or the flow of trade between each country pair).
A node with a high betweenness centrality connects many nodes of a network; using this measure, the most important node is that which is on the most paths connecting any two nodes. Closeness centrality refers to the mean distance between one node and all other nodes; using this measure, the most important node is that which has the shortest average distance between itself and all other nodes.Footnote 1
The most common centrality measures focus on the number of connections a node has to other nodes. The sum of these connections gives the degree of a node, and a node with higher degree is assumed to have more influence than one with lower degree. Measuring only the sum of connections of a node is called degree centrality or, in a directed network, indegree or outdegree centrality. Degree centrality is appealing because of its simplicity, but it does not give an indication of a node’s position in the larger network: a node may have high degree centrality, but if those with which it is connected have few connections, the node probably is not very important. Similarly, a node may not be connected to many other nodes, but if the nodes to which it is connected are themselves connected to many nodes, that node may be influential. A node can also be influential if it connects parts of a network that otherwise would not be connected.
Instead, a node’s influence is also a function of the connections of that node’s neighbors, its neighbors’ neighbors, and so on. Many measures therefore take into account the importance of a node’s neighbors to calculate a node’s centrality, the idea being that an important node has neighbors that are also important. There are various ways to calculate these measures, some of the most common being eigenvector centrality, Katz centrality, PageRank, and k-core; see Newman (Reference Newman2010) for a mathematical explanation of these measures. For simplicity through the rest of the paper, I call these measures global centrality measures.
Eigenvector, Katz, PageRank, and k-core centrality require having data on every connection in a network. For example, studying how networks affect adolescent health in a high school would require knowing not just demographic data about each student but also with whom students interact; acquiring those data require large investments in time and money, and the cost multiplies with the duration of the study. As the network being studied grows, e.g., if one wants to study behaviors on Facebook or Twitter, calculating these centrality measures becomes exceedingly costly. Given this difficulty, degree centrality is the most common measure of centrality in large-scale studies, especially those using social media datasets (Kwak et al. Reference Kwak, Lee, Park and Moon2010; Garcia-Herranz et al. Reference Garcia-Herranz, Moro, Cebrian, Christakis and Fowler2014).
Degree centrality’s appeal is therefore based on its ease of measurement, not its measurement validity. While it does correlate highly with global centrality measures (Bonner et al. Reference Bonner, Gilbert, Shi and Adamic2008), that correlation masks heterogeneous effects. Intuitively, a node with low degree could be connected to a node with very high degree, meaning whatever that node does could influence the larger network through its connection with the more well-connected one; degree centrality does not capture this second-order effect, much less third or fourth-order ones. In a study using complete network data from Twitter, Facebook, Livejournal, and the American Physical Society, Pei et al. (Reference Pei, Muchnik, Andrade, Zheng and Makse2014) find that global centrality measures, especially k-core centrality, better identify which nodes spread the most information (Pei et al. Reference Pei, Muchnik, Andrade, Zheng and Makse2014).Footnote 2 Degree centrality and PageRank are shown to create different rankings in a study of 41 million Twitter users from 2009 (Kwak et al. Reference Kwak, Lee, Park and Moon2010). In other words, while the correlation between degree centrality and global centrality measures is high, the rank ordering correlation is much lower.
This paper introduces a measure that uses more data than degree centrality but less than global centrality measures. Specifically, a node’s neighbor cumulative indegree centrality (NCC) is the sum of the indegree of the node’s neighbor’s. Formally:
For each node
![]() $i$
, the neighbor cumulative indegree centrality is the sum of the indegree centrality
$i$
, the neighbor cumulative indegree centrality is the sum of the indegree centrality
![]() $d_{j}$
for each neighbor
$d_{j}$
for each neighbor
![]() $j$
. This measure is first introduced in Pei et al. (Reference Pei, Muchnik, Andrade, Zheng and Makse2014) and has been used independently in Kim et al. (Reference Kim, Hwong, Stafford, Hughes, O’Malley, Fowler and Christakis2015), though it does not appear to have yet gained widespread use. To the best of my knowledge, this paper is the first in political science to use it. Figure 1 presents an illustration of NCC.Footnote
3
$j$
. This measure is first introduced in Pei et al. (Reference Pei, Muchnik, Andrade, Zheng and Makse2014) and has been used independently in Kim et al. (Reference Kim, Hwong, Stafford, Hughes, O’Malley, Fowler and Christakis2015), though it does not appear to have yet gained widespread use. To the best of my knowledge, this paper is the first in political science to use it. Figure 1 presents an illustration of NCC.Footnote
3
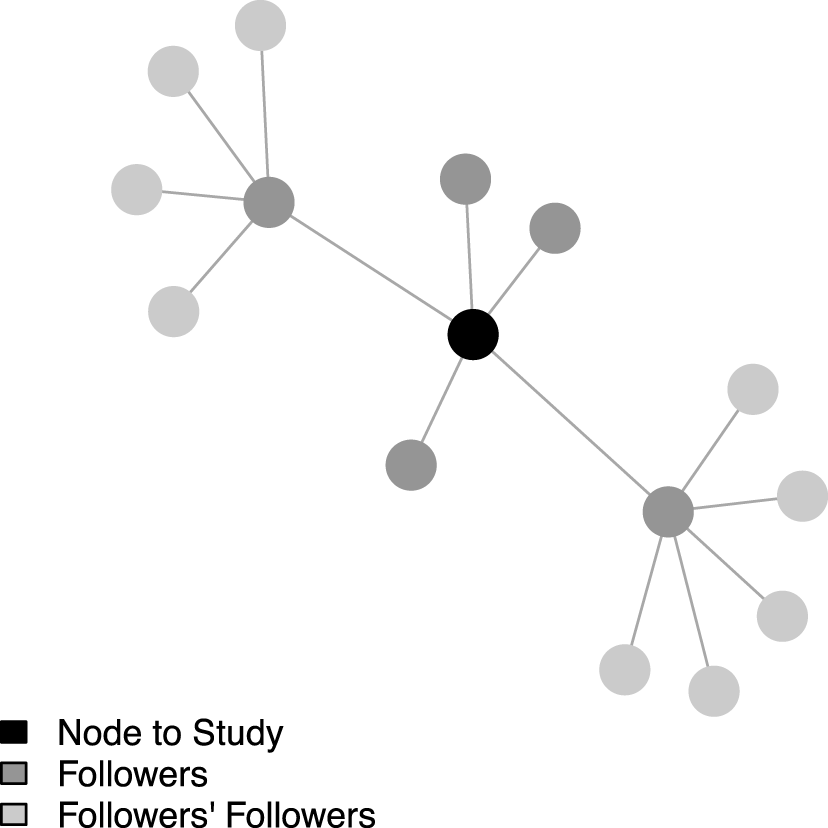
Figure 1. Degree centrality
![]() $=$
5; neighbor cumulative indegree centrality
$=$
5; neighbor cumulative indegree centrality
![]() $=$
9.
$=$
9.
2.1.1 Simulations
A series of simulations demonstrates that ranking by NCC instead of indegree centrality more accurately recovers rankings based on eigenvector, PageRank, and closeness centrality. (Section 3 explains why rankings are preferred instead of raw scores.) For a series of networks ranging in size from 100 to 10,000 nodes, a power-law degree distribution with a scaling exponent of 2.089, the scaling parameter found from three hours of streamed tweets, is used to assign connections between nodes, and each network contains ten times as many edges as nodes. The neighbor cumulative indegree, eigenvector, PageRank, and closeness centrality of each node is then measured, and a node’s influence is then determined by its rank ordering based on each centrality score. For each network, a node’s position in the NCC and indegree rank orderings is compared to its position in the rank ordering based on eigenvector, PageRank, and closeness centrality. This comparison generates two bivariate graphs, one for NCC ranking and another for indegree centrality. The correlation coefficients from those graphs are compared to each other for each network.
Figure 2 shows the result of this simulation. It shows that the rank ordering of nodes generated by neighbor cumulative indegree centrality preserves 70 to 90 percent of the rank ordering created by eigenvector, PageRank, and closeness centrality. Compared to indegree centrality, this correlation represents a 7.89% improvement in rank correlation for PageRank centrality, 26.35% for closeness, and 26.77% for eigenvector. These results corroborate the empirical results of Pei et al. (Reference Pei, Muchnik, Andrade, Zheng and Makse2014).
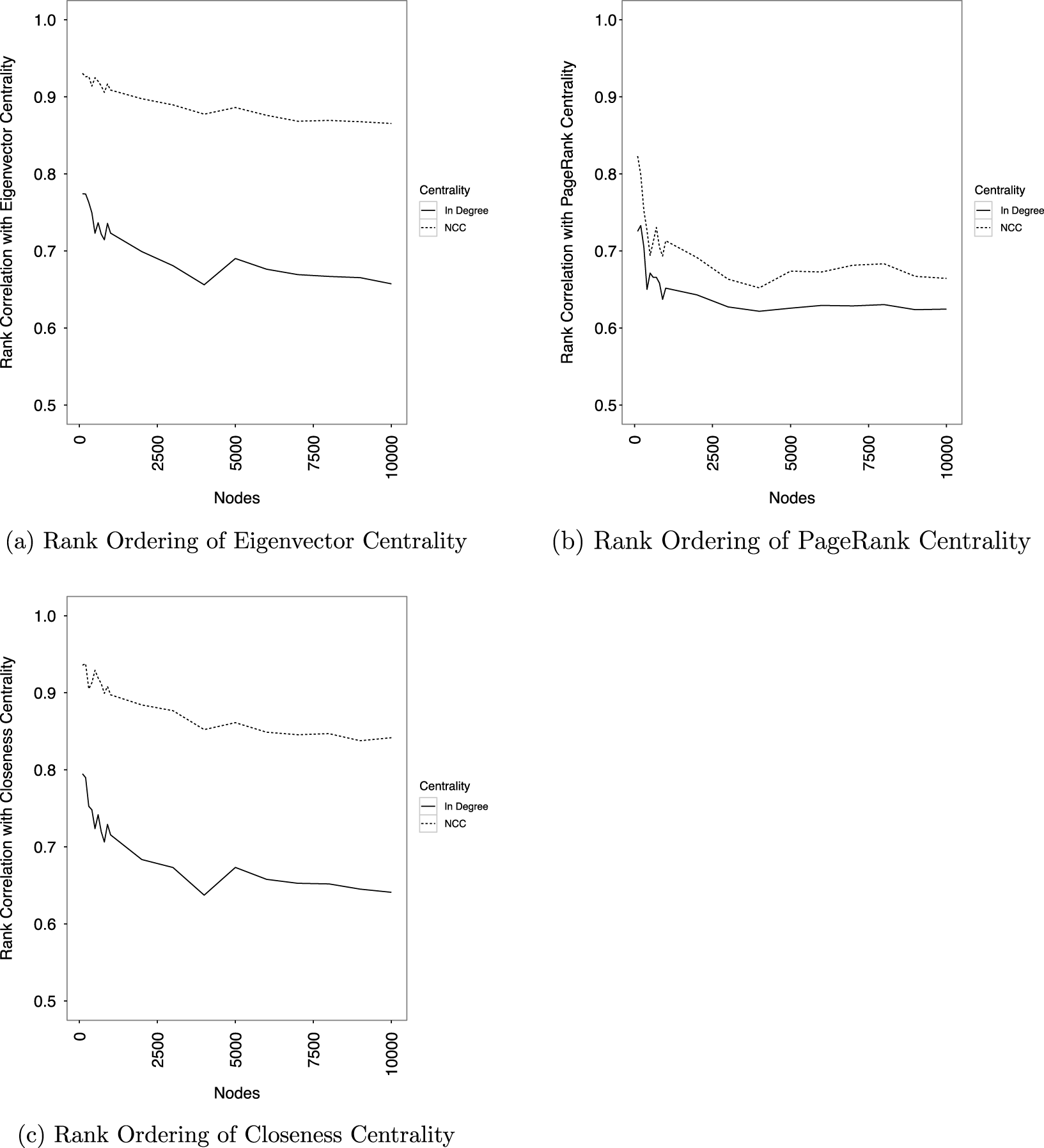
Figure 2. Neighbor cumulative indegree centrality better measures influence than indegree centrality.
In many situations, however, the complete network is unavailable. I therefore also simulated networks, calculated global centrality measures, sampled nodes from the network, and compared the rank correlation of NCC and indegree centrality to those global centrality measures. Figure 3 shows these results comparing NCC and indegree centrality to eigenvector centrality, and Section 1 of the Supplementary Materials shows the same for closeness and PageRank centrality. In sampled networks, NCC ranking continues to outperform indegree centrality ranking.

Figure 3. NCC and eigenvector ranking with sampled data.
2.2 Over time
To measure neighbor cumulative indegree centrality over time, a network needs to be measured at different points in time. If the network requires in-person measurement—surveying a school or canvassing a neighborhood, for example—that sampling procedure can be repeated and NCC measured a second time. If the network is measured digitally, such as via Twitter, the steps required to measure NCC longitudinally most likely differ from the steps required to measure it initially. Because Twitter is one of, if not the, most common digital sources of network data, this section explains how to measure NCC over time using that platform.Footnote 4
Twitter does not reveal when one user starts to follow the other, so a researcher only knows that a connection exists but not when it formed.Footnote 5 Two pieces of information from the REST API ameliorate this situation. First, the list of followers (or friends) that Twitter provides is sorted in reverse chronological order, meaning one knows the relative ordering of connection dates.Footnote 6 Second, the REST API provides the date when an account was created. These two pieces of information make it possible to accurately reconstruct when connections are formed.
Using the date followers join Twitter allows for the approximation of connection formation date, as shown in Table 1; because one does not know the precise date a connection forms, bounds around the actual date need to be created.Footnote 7 The lower bound of the bounds is calculated as follows: for each follower in a user’s follower list, the earliest that follower could have started following is the most recent Twitter joining date of all followers below that follower; this date is the lower bound of the estimate of the true connection forming date.
Estimating the upper bound on the connection formation date is more difficult; in fact, the upper bound itself has a lower and upper bound. The upper bound on the upper bound (UBUB) of the estimate of the connection formation date is the day the data were downloaded, as it is theoretically possible an account’s followers all started following that account earlier that day. The lower bound on the upper bound (LBUB) of the estimate of the connection date is the first Twitter joining date greater than that follower’s Twitter joining date for the followers above that follower in the follower list. If no follower matches this criteria, the LBUB is the day the data were downloaded.
Table 1 clarifies this algorithm, and Section 2 of the Supplementary Materials provides pseudocode for it. Suppose User 1 has followers A, B, C, D, E, F, G, H, and I, with A the newest follower and I the oldest. Follower A joined Twitter on 12.29.2010 but could not have followed User 1 before 12.07.2013 because that is the most recent Twitter joining date of the nine followers. Follower C joined at the same time as A but could have started following User 1 as early as 06.20.2012 because the latest any of Followers C through I joined Twitter was that day. Follower G’s earliest possible connection date is the same as the day it joined Twitter because neither of the two already existing followers joined Twitter after Follower G. These dates, the third column of Table 1, are the lower bound of the estimate of the connection formation date.
The LBUB and UBUB of the estimate of the connection date is calculated as follows. Follower A’s latest possible connection date is whatever day the follower list was downloaded, since Follower A is the newest follower of User 1; the same is true of Follower B because no subsequent follower (which is only Follower A) joined Twitter after Follower B. We can infer that Follower I connected to User 1 at least no later than 01.25.2011 because the first follower who connected with User 1 and had a Twitter joining date later than Follower 1 (Follower G) joined Twitter on 01.25.2011. Since Follower G could not follow User 1 before 01.25.2011, the LBUB for Follower I and User 1 is 01.25.2011; because we do not observe when Follower I actually started following User 1, the UBUB is the day the followers list was downloaded from Twitter. The same is true for Follower H; Follower H could not have connected to User 1 before Follower I, even though Follower H joined Twitter earlier, because Follower H is closer to the top of the follower list. The LBUB for Follower E and User 1 is 06.20.2012, the first joining date of Followers A to D that is greater than Follower E’s joining date of 08.16.2009.
Table 1. Inferring follower relationship formation.

* From Twitter’s GET followers/ids endpoint on the REST API.
![]() $^{+}$
From Twitter’s GET users/lookup.
$^{+}$
From Twitter’s GET users/lookup.
![]() $^{\#}$
Calculated by the researcher.
$^{\#}$
Calculated by the researcher.
The inability to establish a precise upper bound for the following date is theoretically problematic but pragmatically not. To return to Table 1, a researcher interested in the network of User 1 on 01.26.2011 can be certain that User 1 had at most two followers on that day. Theoretically, User 1 may have had 0 followers, if they all started following User 1 after 01.26.2011. But users gain followers over time; while bursty, users gaining all their followers on one day, which is what would be necessary for the upper bound of the confidence interval, is rare to nonexistent (Hutto, Yardi, and Gilbert Reference Hutto, Yardi and Gilbert2013; Antoniades and Dovrolis Reference Antoniades and Dovrolis2015; Myers and Leskovec Reference Myers and Leskovec2014). Section 4.1 uses a dataset where users’ true number of followers are known to show that the estimate accurately recovers the true number of followers. Meeder et al. (Reference Meeder, Karrer, Borgs, Ravi and Chayes2011) show that the estimate of the lower bound of the connection time accurately recovers the true connection time for celebrity accounts. Section 3 of the Supplementary Materials show that using the earliest latest date a connection forms quickly converges to the earliest date for accounts with hundreds of followers.
Meeder et al. (Reference Meeder, Karrer, Borgs, Ravi and Chayes2011) provide an analytic explanation of this process, and this paper builds on that work in three ways. First, it provides a method for estimating the upper bound of the follower connection date formation. Having a lower and upper bound for follower connection dates allows for more precise estimation of connection formation, though the bounds approach each other as the number of followers increases. Second, Meeder et al. (Reference Meeder, Karrer, Borgs, Ravi and Chayes2011) work with celebrity accounts because they rapidly gain followers; the accounts in this sample show that this technique extends beyond celebrities. Third, the results show that measuring true changes in followers is accurate when combining the streaming and REST APIs, whereas Meeder et al. (Reference Meeder, Karrer, Borgs, Ravi and Chayes2011) use the REST API to crawl specific accounts. Since a large number of studies using Twitter, perhaps most, start with data from the streaming API, this paper provides a more realistic validation for estimating connection formation dates.
3 Ranking, NCC, and When to Use Ranked NCC
Ranking nodes based on a centrality measure is preferable to using raw centrality measures, and ranking based on NCC is preferable to ranking on indegree centrality, including in studies of offline social networks. NCC is to be preferred over global centrality measures when global network data are not available; global network data are rarely available because of cost.
3.1 Ranking instead of raw score
There are two reasons to evaluate nodes by their rank instead of the absolute value of NCC. First, ranking individuals facilitates interpretation by controlling for unobserved heterogeneity. For example, individuals in the United States will have higher degree centrality and NCC than individuals in Suriname because the United States has more people; a user in Suriname with the same number of followers as one in the United States should therefore be more influential. Rank ordering at the country level, or whatever grouping makes the most sense for the research question, therefore acts as a fixed effect. Similarly, individuals in both countries should see an increase in their degree centrality and NCC because of population growth.Footnote 8 Increases indegree centrality or NCC could erroneously be ascribed to a variable of interest when in fact the changes are a time effect. Rank ordering is therefore more likely to change as a result of a node’s behaviors instead of unobservables. If using unranked NCC or indegree centrality, individuals from a more populous setting will drive results.
Second, even if there is no concern about unobserved heterogeneity (all the observations are from the same school or country, for example), ranking has greater measurement validity than absolute values for most, perhaps all, social behaviors. Forbes publishes the 500 wealthiest individuals and largest corporations, not those worth $1 billion or with revenue over an arbitrary threshold. Olympic medals are given for the top three finishers, not everyone attaining a certain score or finishing below a certain time. Search engines return pages in rank order of estimated relevance, not just those pages above a relevance threshold and certainly not randomly sorted. An A on an exam is less impressive if that is the modal grade than if a C is most common. In other words, social outcomes such as happiness, status, or influence, to name a few, derive from comparison to others, not to an abstract notion of those concepts (Brickman, Coates, and Janoff-Bulman Reference Brickman, Coates and Janoff-Bulman1978; Veenhoven Reference Veenhoven1991; Adler et al. Reference Adler, Epel, Castellazzo and Ickovics2000). For researchers interested in influence in a network, relative influence (ranked NCC or indegree centrality) should therefore also matter more than absolute influence (raw NCC or indegree centrality).
Using ranking to evaluate nodes does not lead to different inferences than using absolute values. Sampled networks accurately recover the ranking of nodes based on degree, betweenness, and closeness centrality (Kim Reference Kim2007). A canonical simulation of scale-free network growth, the Barabási–Albert model, relies on new nodes knowing the degree of existing nodes (the “preferential attachment” mechanism) (Barabási and Albert Reference Barabási and Albert1999); it turns out that the same network can grow when new nodes only know the rank of existing nodes (Fortunato, Flammini, and Menczer Reference Fortunato, Flammini and Menczer2006). Even in gene regulatory networks, ranking by degree strongly correlates with complete centrality measures (Koschutzki and Schreiber Reference Koschutzki and Schreiber2008).
3.2 NCC instead of indegree centrality
Neighbor cumulative indegree centrality has three advantages that compel its usage: it recovers influence rankings of global centrality measures better than indegree centrality, does so at a significantly lower cost than those global centrality measures, and allows for centrality analysis on large offline networks.
First, the key benefit of NCC is that it recovers other centrality measures that require complete network data while using much less data. NCC works because it captures information on nodes up to two degrees away from the node for which NCC is calculated, incorporating much of information that global centrality measures incorporate while minimizing data requirements. The global centrality measures operate recursively, meaning they capture information on a node’s 3rd, 4th, 5th, ... nth connections. While the contribution to importance of a node’s third to
![]() $n$
-th degree connections may matter, these far-away neighbors should have less of an effect than a node’s immediate and second-degree connections; empirically, this is the case (Christakis and Fowler Reference Christakis and Fowler2012). On the other hand, indegree centrality, as shown in the previous sections, generates misleading inferences about influence.
$n$
-th degree connections may matter, these far-away neighbors should have less of an effect than a node’s immediate and second-degree connections; empirically, this is the case (Christakis and Fowler Reference Christakis and Fowler2012). On the other hand, indegree centrality, as shown in the previous sections, generates misleading inferences about influence.
Another way to think about NCC is that it takes advantage of the power-law distribution of network degree that creates the friendship paradox (Feld Reference Feld1991). Since a person’s contacts will have more contacts, on average, than the original person, it is possible to monitor the emergence of behaviors by taking a sample of individuals and sampling the people to whom they are connected (Christakis and Fowler Reference Christakis and Fowler2010; Garcia-Herranz et al. Reference Garcia-Herranz, Moro, Cebrian, Christakis and Fowler2014).
Second, using much less data markedly lowers the cost of data collection. For example, Larson et al. (Reference Larson, Nagler, Ronen and Tucker2016) collect the Twitter social network out to two degrees (the connections’ connections) of 1,764 accounts from France, resulting in 199,126,639 additional nodes (111,618.07 connections per original account). The first-degree crawl this paper performs for the 21 activist accounts (discussed shortly) generates 90,863.52 connections per account. Gathering enough data to start analyzing network structure therefore requires at least 22.84% more data; because this paper samples prominent accounts while Larson et al. sample more randomly, the computation differences are probably greater than 22.84%.
While Larson et al. (Reference Larson, Nagler, Ronen and Tucker2016) do not undertake centrality analysis because it is not the focus of their research question, note that they would still have biased results because they do not have complete data. A comparison of sample strategies on four different networks finds that each sampling procedure requires a large network sample (over 50% of all nodes) before that sample’s network characteristics converge to the full network’s value (Lee et al. Reference Lee, Kim and Jeong2006). They could, however, calculate NCC, and because Twitter provides the number of followers for each account, calculating NCC from Twitter only requires a one-degree crawl.
Third, the need to collect data on all connections in a network in order to calculate centrality means that offline networks that have been studied are small. A canonical example is Zachary’s karate club, where the social interactions of 34 members were observed over multiple years to understand why the club cleaved (Zachary Reference Zachary1977). A seven year study of dolphin social networks in a New Zealand fjord followed 83 dolphins (Lusseau et al. Reference Lusseau, Schneider, Boisseau, Haase, Slooten and Dawson2003). Scholars have made productive use of offline social network data for the 12,067 individuals in the Framingham Heart Study, though that study has received decades of generous institutional support that could not be replicated by an individual researcher (Christakis and Fowler Reference Christakis and Fowler2007, Reference Christakis and Fowler2008; Fowler and Christakis Reference Fowler and Christakis2008).
NCC increases the scale of network analysis that can be conducted without computers. For example, studies of social networks and political participation using surveys ask participants if they know people who also participated (McAdam Reference McAdam1986; Opp and Gern Reference Opp and Gern1993) or observe the participation of individuals known to be connected to those treated by a survey instrument (Nickerson Reference Nickerson2008) or online mobilization messages (Bond et al. Reference Bond, Fariss, Jones, Kramer, Marlow, Settle and Fowler2012). These studies do not, however, ask whether influence varies by how central individuals are in a network, as determining that centrality would have required each survey respondent to identify their friends, surveying those friends, asking those friends to name their friends, survey the friends’ friends, and so on. Instead, if the survey asks each respondent to estimate the number of friends each friend has, the researcher can calculate NCC. This approach has been used in one study to optimize the spread of positive health behaviors, allowing researchers to identify influential individuals to treat (Kim et al. Reference Kim, Hwong, Stafford, Hughes, O’Malley, Fowler and Christakis2015). Since the data to calculate NCC can be gathered at the same time a survey is administered, centrality in larger offline networks can now be studied by smaller teams of researchers. Nickerson (Reference Nickerson2008), for example, surveyed 956 households, while Opp and Gern (Reference Opp and Gern1993) interviewed 1,300 individuals.
3.3 When to use
Neighbor cumulative indegree centrality is best suited for situations in which the researcher has a sampled network (which is most of the time) and can measure the number of connections a node’s connections has.
Online social networks commonly provide the number of accounts a node follows or is followed by. For example, both Twitter and Instagram provide both sums as part of the user profile data. A researcher therefore only needs to download the user profile information of each account in a follower or following list in order to calculate the NCC of the accounts being studied. For example, the 21 accounts analyzed here have 1,908,134 followers, and those followers have a maximum of 506,821,726 followers. Calculating NCC for the 21 accounts does not require downloading 506,821,726 edges, however, as Twitter provides the number of followers as part of the profile information of each of the 1,908,134 first-degree followers. Recovering those nodes’ centrality ranking that would be obtained with complete network data is therefore feasible with only a one-degree breadth first crawl.
Moreover, the lack of perfect correlation between NCC rank and rank based on complete centrality measures is due to change in rank for nodes with few connections; rank is more stable for well-connected nodes than peripheral ones (Kim Reference Kim2007; Cha et al. Reference Cha, Haddadi, Benevenuto and Gummadi2010). Because degree is power-law distribution, gaining 10 connections when one only has 10 will affect one’s rank much more than gaining 10 when one has 1,000,000. For political scientists, this means that inferences based on well-connected groups of people—“members of Congress or the media”, for example—will be more precise than for other groups. Precisely what “well-connected” means, however, is an open question. In this way, the use of NCC rank cannot circumvent a perennial issue: people on the margins of society are difficult to study, sometimes intentionally so.
When offline social network data are gathered, a researcher can ask an individual to estimate the number of friends his or her friends have. So long as those estimates are answered without bias, the resulting NCC rank of each respondent will approximate the rank that would be measured if the researcher counted the friends’ friends him- or herself. Collecting these data would require only one additional survey question or one more behavior to track if the researcher gathers data via participant observation. Relying on in-person data collection also makes it easier to study those who maintain few social connections.
If a researcher has complete network data (all nodes, all connections of those nodes, all those connections’ connections, and so on), then it is preferable to use a global network centrality measure (eigenvector, PageRank, closeness, etc.) that takes advantage of the data. This situation rarely holds, however. Only in settings with few nodes or that can be closely monitored, such as a club, workplace, or school, will the entire network graph be observable. Even studies which use online social networks rarely observe second-degree effects of a treatment (see Bond et al. (Reference Bond, Fariss, Jones, Kramer, Marlow, Settle and Fowler2012) for an exception) or crawl the entire social graph (Larson et al. (Reference Larson, Nagler, Ronen and Tucker2016), the most extensive recent crawl of Twitter, stops at friends of friends).
4 Political Entrepreneurs and Protest Mobilization
From Egypt and Bahrain, 42 activists representing five social movements were identified, 19 of whom were active on Twitter prior to each country’s first protests. In Egypt, activists from the April 6th youth movement, the No Military Trials campaign, and the Anti-Sexual Harassment movement were chosen; in Bahrain, the human rights community and February 14th youth coalition were chosen, though only the human rights community was active on Twitter before the start of protests. The final 19 activists represent the three social movements in Egypt and Bahrain’s human rights community. These movements were chosen because they were active before, during, and after each country’s main protest period, and individual accounts were identified in collaboration with a colleague at a British university; for more detail on the movements and accounts, see Fowler and Steinert-Threlkeld (Reference Fowler and Steinert-Threlkeld2016) for more detail. Two Bahraini government accounts were also identified and collected, raising the final number of accounts under analysis to 21.
Their position in the larger Twitter social network and their behaviors are observed from January 11, 2011 to April 5, 2011. Measuring NCC requires working with Twitter’s REST API. I also purchased these accounts’ tweets from early 2011 to confirm the accuracy of NCC measure; each tweet provides data on how many followers an account has at the time it is created, providing a ground truth to which to compare the followers’ estimate (Shulman Reference Shulman2011). See Section 5 of the Supplementary Material for a discussion of these accounts, why they were chosen, the Arab Spring, and more information on acquiring their data.
4.1 Reconstructing daily network change
This section demonstrates that the procedure in Section 2.2 accurately measures the true number of followers and reveals changing network structure. The results are presented using the lower bound of the estimate of the connection date (column 3 from Table 1), and Section 3 of the Supplementary Materials show that results do not change if using the lower bound of the upper bound of the estimate of the connection date (column 4 from Table 1).
There are two ways to measure a user’s change in followers over time: either observe that user in real time (with the streaming API) while frequently downloading their followers’ list (via the REST API), or estimate, later and indirectly, that change. The former is most precise but requires that the researcher knows which accounts he or she is interested in before an account is observed for a study. Estimating the change indirectly, through the REST API, is therefore how most longitudinal analyses will proceed. This section demonstrates that estimating indirectly the change accurately recovers the true number of followers and can show daily change in network structure, substantiating the methodology explained in Section 2.2.
Figure 4a shows that the post hoc estimated number of followers linearly predicts the true number of followers. The estimated number of followers under-predicts the true number because users can stop following an account or delete their account, the followers list was downloaded after the period of study, and Twitter removes users from the followers list once they stop following an account.
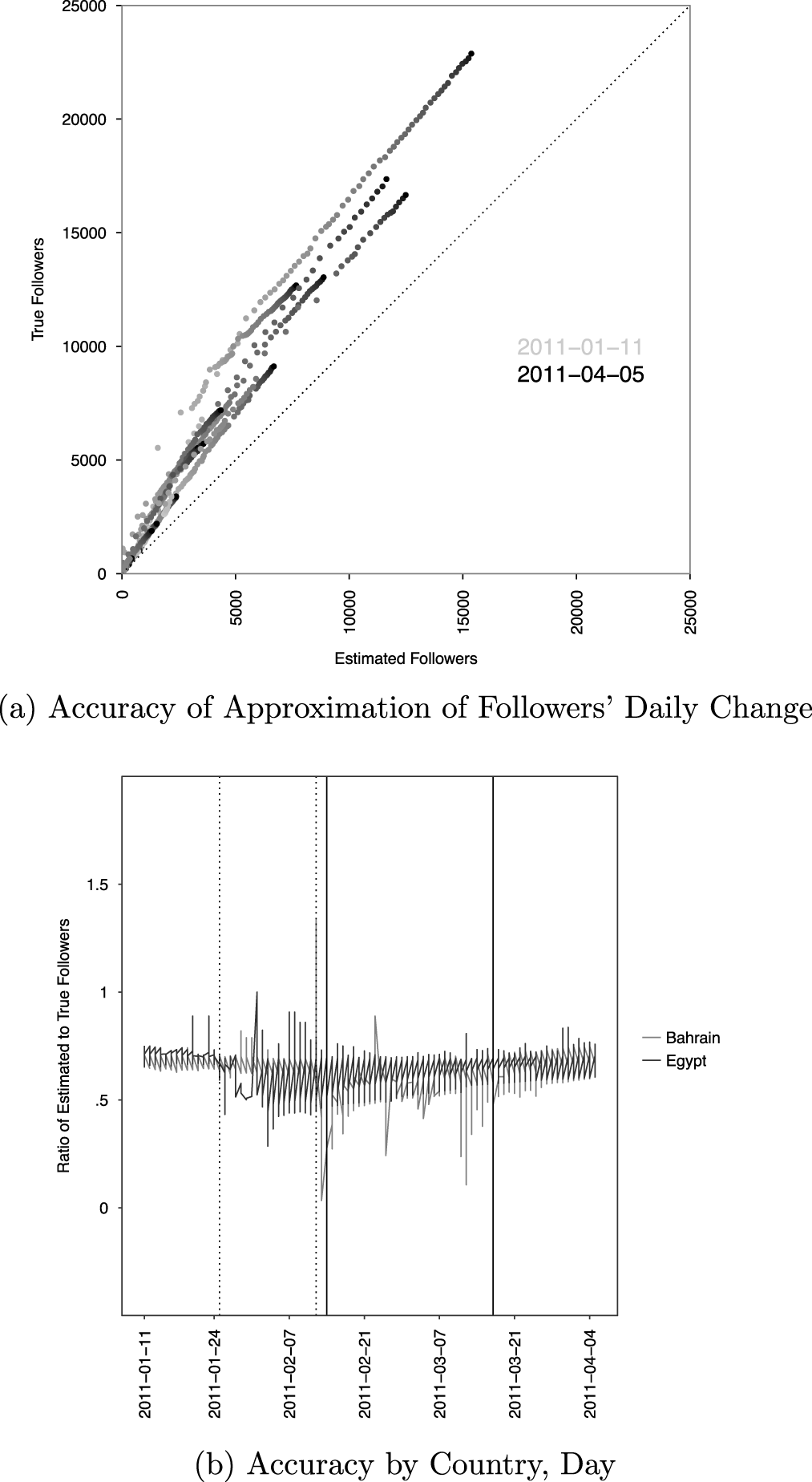
Figure 4. Verification against ground truth data.
In Figure 4a, accounts are shaded from light to dark gray based on how close to April 5, 2011 they are.Footnote 9 The estimated number of followers explains 98.09% of the variance in the number of true followers, with half of the remaining variance explained by group fixed effects; both these estimates are based on a linear model not shown here.Footnote 10 The residual increases as a function of the estimated number of followers, but this heteroskedasticity is constant as a percentage of an account’s followers.
Figure 4b shows that the estimated number of followers is usually 67.53% of the true number of followers. This relationship holds whether or not the results are pooled by country; aggregating observations by group does not change the trends. The dashed lines correspond to the start and end of protests in Egypt, the solid in Bahrain. The post hoc measure performs less consistently, though does not appear biased, during these protest periods, suggesting that the measure may perform less well when the number of followers fluctuates rapidly. Overall, the post hoc measure of followers consistently approximates the true measure, suggesting it can be used when the true number of friends is not observable.
4.2 Daily changes in NCC
To measure neighbor cumulative indegree centrality, the user ID of each of the 21 seed account’s followers was downloaded from Twitter’s GET users/ids endpoint, returning 4,229,373 results containing 1,908,134 unique followers. Each user ID was then submitted to Twitter’s GET users/lookup endpoint, providing data such as when the user joined Twitter, their self-reported location, their default language, and how many tweets they have authored. These first-degree followers themselves have 506,821,726 followers. Since downloading the second-degree connections would require six months, and weeks more to download metadata for each ID, data on second-degree connections were not acquired.
Figure 5 presents the change in neighbor cumulative indegree centrality over three months in Bahrain and Egypt. The first vertical line represents the start of protests, the second the end. Each country’s legend is ordered from highest to lowest values of NCC at the end of the period. Color figures are in Section 4 of the Supplementary Materials.

Figure 5. Reconstructed temporal change in influence.
A few results emerge from Figure 5. In both countries, relative influence is stable: the rank ordering of NCC on January 11, 2011 looks very similar to that on April 5, 2011. Even though every account except for @Ribeska gains NCC, very few gain influence at a quicker rate than their peers. In Bahrain, a notable change is @angryarabiya, who moves from second least influential to fifth most; that account belongs to the daughter of Nabeel Rajab (@NABEELRAJAB), a human rights advocate who led—he is now imprisoned—the Bahrain Center for Human Rights (@BahrainRights). The Ministry of the Interior’s account, @moi_bahrain, is the fourth most influential at the end of the study, an increase of two spots. @byshr, the account of the Bahrain Youth Society for Human Rights, experiences the steepest decline, moving from third to last. Egypt’s relative ordering is more stable. @Shabab6april experiences the greatest change in NCC, moving from fifth to third. @monasosh experiences a large increase in absolute influence, but she only moves from the third to second most influential account.
Both countries’ accounts also experience the greatest changes in NCC and rank ordering around their protest periods. Each country’s users start to gain influence days before the start of protests. Most continue to gain influence during the protest period, and some stabilize after while others continue to gain influence.
Finally, comparing the NCC across Bahrain and Egypt reveals differing network properties. The Bahrain accounts start and end with lower average NCC than the Egyptian ones. Egypt, on the other hand, has higher variance in NCC. The three least influential Egyptian accounts, the relative ranking of which do not change, are accounts for individuals associated with the Anti-Sexual Harassment movement. That movement has been more peripheral to Egyptian politics than those sampled in Bahrain. Excluding those three, the Egyptian accounts have greater influence and lower variance than the Bahraini ones. Why countries’ networks have different structural properties is outside of this paper’s scope, but has started to receive some attention (Zeitzoff, Kelly, and Lotan Reference Zeitzoff, Kelly and Lotan2015).
4.3 Individual behavior and changes in NCC
The temporal change of neighbor cumulative degree centrality can be combined with accounts’ tweeting behavior to analyze if certain patterns of behavior change an account’s influence in a network.
Table 2. Individual correlates of structural position.
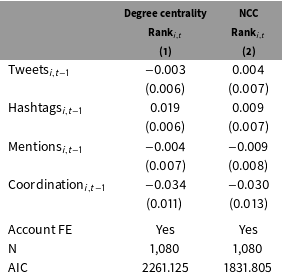
All models are ordered logit with a ranked dependent variable.
A negative sign means a node becomes more influential.
Model 1 with a lagged dependent variable fails to converge.
Model 2 with a lagged dependent variable has the same results.
Table 2 reveals that the effect of individual behaviors varies depending on which measure of centrality is used. Table 2 shows the results from regressing measures of the 21 accounts’ position in their Twitter network on measures of their behavior and account fixed effects. The dependent variable is the rank of an account on a day, depending on whether the measure is degree centrality (column 1) or neighbor cumulative degree centrality (column 2). The independent variables are the number of tweets from an account, the number of tweets with hashtags, the number of tweets that mention another user, the number of tweets that coordinate protest activity, and account fixed effects.Footnote 11 Because the dependent variable is a ranking, a negative coefficient means that an increase of that variable corresponds to increased influence.
Table 2 shows that more tweets with hashtags are not associated with greater influence. The results in Table 2 show that a model of influence which relies on degree centrality will suggest that an account which tweets more using hashtags will have a lower ranking than if it did not. While some work has argued that the best way to increase one’s influence on Twitter is to use hashtags to make one’s tweets part of a larger conversation (Kwak et al. Reference Kwak, Lee, Park and Moon2010; Bruns and Burgess Reference Bruns and Burgess2011; Gonzalez-Bailon, Borge-Holthoefer, and Moreno Reference Gonzalez-Bailon, Borge-Holthoefer and Moreno2013), this finding corroborates other researchers who find that specializing in a particular topic on Twitter is how accounts gain influence (Cha et al. Reference Cha, Haddadi, Benevenuto and Gummadi2010). While hashtags may decrease one’s ranking based on the number of followers (Column 1), it does not appear to do so based on the followers those followers have (Column 2). In other words, using hashtags may cause an account to gain followers but not at a greater rate than other individuals in the network. Moreover, those followers do not have many followers, causing no change in influence as measured by NCC.
Both models find that more tweets coordinating protests lead to an account being ranked more highly. On the other hand, the only variable which leads to an increase of NCC rank (column 2) is the number of tweets about protest coordination. This result is in line with other work that has found that user’s influence rank, measured by retweets and mentions, increases as they specialize in tweeting about one topic (Cha et al. Reference Cha, Haddadi, Benevenuto and Gummadi2010). Note as well that a model of NCC Rank fits better than a model of Degree Centrality Rank.
5 Other Applications
This section details other domains in which longitudinal neighbor cumulative indegree centrality is useful.
5.1 Hidden influentials
Network studies often are interested in identifying which nodes facilitate diffusion. While it is common to analyze highly central nodes, recent work on protest diffusion suggests that accounts with low outdegree but high indegree may also be influential; these accounts are called “hidden influentials” and refer to accounts that global centrality measures may miss (Gonzalez-Bailon Reference Gonzalez-Bailon, Borge-Holthoefer and Moreno2013). A slight modification of the NCC measure suggests an alternate method of finding hidden influentials.
Instead of taking the sum of neighbors’ indegree centrality, the median of the neighbors’ indegree identifies accounts whose followers have many followers. NCC favors accounts with many followers, with some weight assigned to how popular those followers are; there thus exists a strong positive relationship between the number of followers and the sum of the followers’ followers. Taking the median of the followers’ followers emphasizes accounts with few followers but whose followers’ followers have many connections; it is preferred to the average so that one or two very popular followers does not bias results. The accounts with a high median number of followers’ followers may be hidden influentials.
Figure 6a shows the simulated distribution of the median NCC against the distribution of followers; these data are the same used in Figure 2. Figure 6b is the same but on the data from the 21 accounts. In both cases, there is a clear decaying relationship between the number of followers and the median NCC. This decaying relationship makes sense, as most individuals in a network have few connections while a few have very many (Feld Reference Feld1991). In the simulated and actual data, however, there are some accounts that have few followers but whose followers have very many followers. These hidden influentials are the data points crawling up the y-axis near x equals 0. Because these data are a for a directed network, these accounts are those who are followed by accounts with many followers even though they themselves are not followed by many.
Using median NCC to identify accounts may reveal nodes in a network which help products diffuse or campaign messages resonate. Marketers understand that diffusion on a network is likely to come from those with many followers, but which of those central individuals will cause diffusion is very hard to predict. This apparent randomness means marketers have to target all “influencers”, a costly proposition (Bakshy et al. Reference Bakshy, Hofman, Watts and Mason2011). Instead, a better approach may be to identify and target those accounts that the influencers follow, as they will be less expensive. Targeting these hidden influentials may be a more attractive option than focusing on the mass of individuals whose weak links to each other otherwise spread information about products (Watts and Dodds Reference Watts and Dodds2007; Bakshy et al. Reference Bakshy, Marlow, Rosenn and Adamic2012).

Figure 6. Median neighbor indegree centrality and hidden influentials.
5.2 American politics
Since President Obama’s 2008 election, scholars have realized the value large datasets have for political scientists (Nickerson and Rogers Reference Nickerson and Rogers2014). Studies which use network concepts to measure behaviors of interest to American politics have traditionally relied on cross-section surveys, and I am aware of no work which uses longitudinal network analysis. The following sections briefly discuss possible applications of NCC.
A large literature examines the conditions under which individuals mobilize to vote; for reviews of it, see Blais (Reference Blais2006) and Jacobson (Reference Jacobson2015). Part of that literature focuses on how individuals’ social connections affect their decision making, with a heavy use of cross-section surveys and field experiments to make causal claims (Huckfeldt and Sprague Reference Huckfeldt and Sprague1987; Lake and Huckfeldt Reference Lake and Huckfeldt1998). Work that incorporates a temporal component focuses on political institutions like Congress or the Supreme Court because they contain few individuals and make data collection relatively easy (Fowler et al. Reference Fowler, Johnson, Spriggs, Jeon and Wahlbeck2007; Rogowski and Sinclair Reference Rogowski and Sinclair2012). Scholars have not, however, been able to study voters in their networks over time. Does an individual’s network position change in response to his or her political beliefs? Is one more likely to vote if someone central to their network does so? If an individual’s friend expresses a differing political opinion, does the centrality of that friend affect the individual’s likelihood to change opinion? Do elections affect the structure of one’s friendship networks? If so, does the effect vary for local, state, and presidential elections? These questions can start to be answered with the methods presented in this paper.
Political parties target voters in order to persuade them to support their candidate, and the methods developed in this paper may help them identify influential individuals to target. Prior to campaigns’ ability to use large datasets to target specific individuals (Hersh and Schaffner Reference Hersh and Schaffner2013; Nickerson and Rogers Reference Nickerson and Rogers2014), campaigns would canvass large groups of people, hoping to create a “ripple effect of social interaction” in their favor (Sprague and Huckfeldt Reference Sprague and Huckfeldt1992, pg. 77). Parties vary their contact based on supra-individual characteristics, such as district or state competitiveness, and have done so since at least 1956 (Panagopoulos and Francia Reference Panagopoulos and Francia2009). The methods developed here, however, could allow a campaign to distinguish influential core supporters from noninfluential ones or find influential individuals socially near a campaign’s core supporters (Holbrook and McClurg Reference Holbrook and McClurg2005). The NCC measure can also identify which peripheral individuals are influential, letting a campaign focus more efficiently on using its resources to persuade them (Chen and Reeves Reference Chen and Reeves2011). The ability to observe communities evolve can alert campaigns to groups of people who have followed their candidate as well as ideologically far ones; assuming those individuals have not decided who to support, targeting them before the competition does would be valuable (Huckfeldt, Mendez, and Osborn Reference Huckfeldt, Mendez and Osborn2004).
6 Conclusion
This paper joins a growing body of longitudinal network analysis in political science, but it is the first, as far I am aware, to analyze individuals at the daily level. Longitudinal network analysis has been used to understand the Great Recession (Oatley et al. Reference Oatley, Winecoff, Pennock and Danzman2013), the effect of international organization of conflict (Hafner-Burton and Montgomery Reference Hafner-Burton and Montgomery2006; Dorussen and Ward Reference Dorussen and Ward2008), the relationship between trade and conflict (Lupu and Traag Reference Lupu and Traag2013), and jurisprudence at the European Court of Human Rights (Lupu and Voeten Reference Lupu and Voeten2012). These studies analyze cases, institutions, or states as their relationships change every year. The population of each is much smaller than the population of people, and focusing on annual change lowers the cost of data collection. NCC allows the researcher to analyze changes in populations heretofore too large to study, and the lower cost of calculating it facilitates the measurement of daily changes.
While multiple online social networks exist that could provide data, this paper focuses on Twitter. Twitter’s global reach, large user base, and data openness make it a common platform for large-scale studies of human behavior. With over 300 million accounts creating 500 million messages per day, it is one of the largest online social networks. Its data are also relatively easy to access, compared to other platforms. While other social media platforms and websites, such as reddit or Instagram, also have easily accessible data, none are as general purpose as Twitter. Though Twitter is the preferred platform for analyses of networks through social media, analyses of network structure with its data are difficult because of how the platform provides data to researchers. Data provided as a streaming sample make structure difficult to see, while Twitter limits how often one can download data on connections between individuals. This paper’s methods work within Twitter’s limits.
While neighbor cumulative indegree centrality captures rank ordering that would be obtained with complete network data, it may still be preferable to have information on more than first-degree connections; for example, one can start topographic analysis with data on connections’ connections (Larson et al. Reference Larson, Nagler, Ronen and Tucker2016). In practice, such information is very costly to obtain. Because the number of connections in a network expands exponentially while Twitter’s rate limits are fixed, computing time increases supralinearly. For the 21 users in this study, their 1,908,134 followers have 506,821,726 followers; at 60 requests per hour returning a maximum of 5,000 followers per request, one computer connection would need just over 70 days to download the list of second-degree followers. Assuming 45% of those are unique (the percentage from the crawl of followers for this paper), one computer would require almost 132 days to download data on each unique user. While this number is probably an overestimate, since some of the second-degree followers may have been followers of one of the other 21 accounts, the rate at which the download time increases as a function of degrees from a seed node is unknown. A complete crawl of Twitter conducted in July 2012 used two machines that could make 20,000 requests per hour, two that could make 100,000, and 550 machines using the normal rate limits; this crawl required four months and four days (Gabielkov, Rao, and Legout Reference Gabielkov, Rao and Legout2014). The four machines with higher rate limits were whitelisted, a now defunct practice by which Twitter gave certain machines preferential access to their data. A similar crawl without whitelisted machines would therefore take about double the time, according to those authors’ estimates.
The main barrier presently facing researchers is therefore programming rate limits. Future work should explore how to approximate neighbor cumulative indegree centrality without having to sample all of a node’s followers. Because of the way Twitter returns data, the approximation would need to work with the newest followers of an account.
This paper has also only treated one direction of an asymmetric network, treating accounts as emitters of information. But individuals also consume information, and the consumption network should change over time as well. The symmetric network—where each connection represents mutual following—will also reveal patterns about more intimate types of relationships. How these networks change over time remains an open question.
Finally, these methods can be used to study offline networks. It is common for studies of networks and political behavior to administer surveys and ask respondents to name their friends (McAdam Reference McAdam1986; Opp and Gern Reference Opp and Gern1993). Modifying this approach, a researcher could ask those the respondent names how many friends they have or even ask the respondent how many friends she or he thinks each of the friends has. This information would be enough to generate NCC scores for the original respondents. Generating the NCC from offline data allows researchers who do not use online social network datasets or who are interested in samples of individuals not on these networks to also approximate centrality when full network data are not available.
Funding
This work was supported by the United States Agency for International Development [(DF)#AID-OAA-A-12-00039].
Supplementary material
For supplementary material accompanying this paper, please visit https://doi.org/10.1017/pan.2017.6.









