1 Introduction
“Updating Bayesian(s): A Critical Evaluation of Bayesian Process Tracing” sought to highlight the gaps between principle and practice for an otherwise promising new methodology. While the article addressed numerous specific issues, the discussion centered on two related problems: (1) the Bayesian process tracing (BPT) literature lacks clear and comprehensive guidelines for implementing its many recommendations, and (2) the literature fails to acknowledge the method’s pitfalls and limitations, and, by extension, the inferential consequences when problems go undetected. The letter responding to “Updating Bayesian(s)” aims to set the record straight and clarify a number of points that the authors view as misunderstandings.
To avoid a spiral of abstract arguments about principles, this response breaks from the point-by-point format of the debate. Instead, I walk through a BPT analysis of the most straightforward example to help get traction on the method in practice: analyzing evidence of a murder. I ask, in the simplest case, does the literature equip a reasonable scholar with the tools to succeed? I begin with a vignette inspired by the response letter. Then, I proceed with the analysis—cataloguing the questions, complications, and problems that arise in both the mathematical and narrative BPT approaches.Footnote 1 Finally, I conclude with an evaluation of my experience using the method and a call to resolve the disconnect between principle and practice in future work.
2 The Scene of the Crime
At 8:15 PM, a victim was found dead in the Echo Park neighborhood of Los Angeles: an area where they had some business, but did not live. Preliminary investigations revealed two possible suspects—Adam and Bertrand—along with a small handful of evidence. One eyewitness claimed to see Adam’s car near the scene of the crime the night the murder was committed. Bertrand’s lawyer handed over credit card receipts placing Bertrand at a dim sum restaurant in the San Gabriel Valley at 7:45 PM. Finally, a search through the victim’s phone revealed a voice mail from Bertrand, asking the victim to drop off some paperwork by 7:30 PM to an office near the crime scene.
3 A State-of-the-Art Investigation
Given an outcome we want to explain (murder), our set of causal factors (Adam and Bertrand), and our pieces of evidence (car sighting, credit card receipts, and a voice mail), this section walks through each stage of a BPT analysis from beginning to end. The method involves three core steps: (1) generating a set of mutually exclusive and exhaustive (MEE) hypotheses, (2) assigning priors and likelihoods, and (3) computing our updated confidence in each hypothesis (relative to each other) conditional on the evidence. I draw on the response letter as well as the broader BPT literature to identify the necessary considerations at each stage of the analysis.
3.1 Hypothesis Generation
The first task is to take our suspects and construct a set of hypotheses about how the murder played out. However, generating hypotheses for this analysis demands special consideration, because Bayesian inference requires an MEE hypothesis set (Fairfield and Charman Reference Fairfield and Charman2017, Reference Fairfield and Charman2019).Footnote 2 Thus, if we fail to construct a—or, perhaps, the?—compliant set of hypotheses at the beginning of the analysis, we must redo it from scratch when we catch our error,Footnote 3 or we risk presenting faulty results at the end.
This requirement has been a critical sticking point in the debate over the merits and “usability” of BPT (Fairfield and Charman Reference Fairfield and Charman2017; Zaks Reference Zaks2017, Reference Zaks2021). Bennett, Fairfield, and Charman’s (Reference Bennett, Charman and Fairfield2021, 2) letter pushes the literature forward by drawing an explicit distinction between causal factors on the one hand, and the functional form of hypotheses, on the other. For example, “only Adam,” “only Bertrand,” and “Adam and Bertrand colluded” represent three distinct worlds, and thus satisfy mutual exclusivity, since we can only be in one. This point clarifies some confusing wording in previous articles,Footnote 4 while also illuminating an important oversight in the broader process-tracing literature (including my own work). Notwithstanding the importance of the new distinction, the process of generating MEE hypotheses, in practice, remains elusive—raising a series of unanswered (or differently answered) procedural questions:
-
1. How can scholars assess the exhaustiveness of their hypothesis set? Where is the line between telling enough stories to have an exhaustive account of the multiverse of functional forms and falling into a problem of infinite regress?
-
2. How can scholars assess whether causal factors are mutually exclusive in their own rightFootnote 5 or whether they might work together to mandate a compound hypothesis?
-
3. If multiple factors can work together, how should we construct the compound hypothesis (or hypotheses)? The BPT literature provides three different strategies for forming compound hypotheses from two causal factors: (1) creating a single, broad compound hypothesis, for example, “A and B colluded”; (2) creating a single compound hypothesis specifying precisely how factors A and B work together; and (3) creating five rivals resembling a Likert scale.Footnote 6 How should we adjudicate among these strategies?
-
4. How useful is this distinction in practice when evidence is equally likely under (and thus unable to distinguish between) multiple hypotheses that include the same causal factors?Footnote 7
-
5. Finally, what are the stakes of satisfying the MEE assumptions? What are the inferential implications of failing to satisfy one or both?Footnote 8
Ultimately, the BPT literature not only omits the stakes of MEE hypothesis generation, but also fails to provide clear and consistent guidelines to do it well. For the sake of proceeding with the analysis, I rely on the hypothesis set Bennett et al. (Reference Bennett, Charman and Fairfield2021, 6) construct:
![]() $H_A$
: Adam committed the crime alone,
$H_A$
: Adam committed the crime alone,
![]() $H_B$
: Bertrand committed the crime alone, and
$H_B$
: Bertrand committed the crime alone, and
![]() $H_C$
: Bertrand lured the victim to the prearranged crime scene where Adam committed the murder.
$H_C$
: Bertrand lured the victim to the prearranged crime scene where Adam committed the murder.
3.2 Assigning Priors and Likelihoods
The next stage in BPT is to assign priors and likelihoods. To assign priors, Fairfield and Charman (Reference Fairfield and Charman2019, 158) recommend asking an intuitive question: “how willing would we be to bet in favor of one hypothesis over the other before examining the evidence?”. Consistent with their advice, and given my lack of background information, I adopt naive priors—placing equal probability on each of the three hypotheses.
This example requires assigning nine likelihoods: the probability of observing each of the three pieces of evidence (
![]() $E_{\text {car}}$
,
$E_{\text {car}}$
,
![]() $E_{\text {rec}}$
, and
$E_{\text {rec}}$
, and
![]() $E_{\text {vm}}$
) in each of the three possible worlds (
$E_{\text {vm}}$
) in each of the three possible worlds (
![]() $H_A$
,
$H_A$
,
![]() $H_B$
, and
$H_B$
, and
![]() $H_C$
). To assess likelihoods, Fairfield and Charman instruct practitioners to “‘mentally inhabit the world’ of each hypothesis and ask how surprising…or expected…the evidence
$H_C$
). To assess likelihoods, Fairfield and Charman instruct practitioners to “‘mentally inhabit the world’ of each hypothesis and ask how surprising…or expected…the evidence
![]() $E_i$
would be in each respective world” (Hunter Reference Hunter1984; Fairfield and Charman Reference Fairfield and Charman2019, 159). Though an intuitive task in theory, the process of assigning numerical (or even narrative) probabilities in practice reveals two problems researchers will likely encounter (beyond the difficulty of conjuring reasonable probabilities in the first place).
$E_i$
would be in each respective world” (Hunter Reference Hunter1984; Fairfield and Charman Reference Fairfield and Charman2019, 159). Though an intuitive task in theory, the process of assigning numerical (or even narrative) probabilities in practice reveals two problems researchers will likely encounter (beyond the difficulty of conjuring reasonable probabilities in the first place).
The first problematic set of quantities are the likelihoods in which the evidence is entirely unrelated to the hypothesis (e.g.,
![]() $P(E_{\text {rec}} | H_A)$
, the probability Bertrand was eating dim sum in the world where Adam committed the murder alone). For researchers taking the mathematical approach, the literature provides no guidance on how to assign likelihoods to a hypothesis when its components are conditionally independent. The laws of probability theory dictate that when
$P(E_{\text {rec}} | H_A)$
, the probability Bertrand was eating dim sum in the world where Adam committed the murder alone). For researchers taking the mathematical approach, the literature provides no guidance on how to assign likelihoods to a hypothesis when its components are conditionally independent. The laws of probability theory dictate that when
![]() $E_i \perp H_j$
,
$E_i \perp H_j$
,
![]() $P(E_i | H_j)$
reduces to
$P(E_i | H_j)$
reduces to
![]() $P(E_i)$
(here, the overall frequency with which Bertrand gets a hankering for steamed pork buns). How should we assess these probabilities in practice?Footnote
9
In this analysis, four of the nine likelihoods exhibit this problem—a problem the response letter sidesteps by using only the narrative BPT approach and jumping straight into the comparison of likelihoods, rather than an individual assessment of each likelihood on its own.Footnote
10
$P(E_i)$
(here, the overall frequency with which Bertrand gets a hankering for steamed pork buns). How should we assess these probabilities in practice?Footnote
9
In this analysis, four of the nine likelihoods exhibit this problem—a problem the response letter sidesteps by using only the narrative BPT approach and jumping straight into the comparison of likelihoods, rather than an individual assessment of each likelihood on its own.Footnote
10
The second problem occurs when researchers ask themselves “how likely am I to observe
![]() $E_i$
under
$E_i$
under
![]() $H_j$
?” and the answer is, “it depends.” For example,
$H_j$
?” and the answer is, “it depends.” For example,
![]() $P(E_{\text {rec}} | H_B)$
—the probability of finding Bertrand’s credit card receipts from an out-of-town restaurant in the world in which he is the sole murderer—depends on (1) whether the murder was premeditated, and (2) whether Bertrand was savvy enough to create an alibi (say, by giving someone his credit card to “treat” them to dinner). If the probability would change substantially based on the answer to those questions, how should researchers proceed? Should we gather more evidence to assess which world we are in? Should each contingency become its own hypothesis? If not, does that violate the exhaustiveness assumption? The literature makes no mention of either problem. It seems, however, that if we ignore the possible (and plausible) world in which Bertrand handed his credit card off to someone else, then we create a false disjunctive syllogism (i.e., affirming by denying) with the remaining hypotheses.Footnote
11
$P(E_{\text {rec}} | H_B)$
—the probability of finding Bertrand’s credit card receipts from an out-of-town restaurant in the world in which he is the sole murderer—depends on (1) whether the murder was premeditated, and (2) whether Bertrand was savvy enough to create an alibi (say, by giving someone his credit card to “treat” them to dinner). If the probability would change substantially based on the answer to those questions, how should researchers proceed? Should we gather more evidence to assess which world we are in? Should each contingency become its own hypothesis? If not, does that violate the exhaustiveness assumption? The literature makes no mention of either problem. It seems, however, that if we ignore the possible (and plausible) world in which Bertrand handed his credit card off to someone else, then we create a false disjunctive syllogism (i.e., affirming by denying) with the remaining hypotheses.Footnote
11
Although I am not convinced that one can or should push past these issues, I assign probabilities to the various likelihoods to proceed with inference. Where possible, I draw on Bennett, Fairfield, and Charman’s reasoning and otherwise I attempt to replicate their logic.Footnote 12
-
•
 $P(E_{\text {car}} | H_A) = 0.65, ~P(E_{\text {car}} | H_B) = 0.1,~ P(E_{\text {car}} | H_C) = 0.65,$
$P(E_{\text {car}} | H_A) = 0.65, ~P(E_{\text {car}} | H_B) = 0.1,~ P(E_{\text {car}} | H_C) = 0.65,$
-
•
 $P(E_{\text {rec}} | H_A) = 0.14,~ P(E_{\text {rec}} | H_B) = 0.005, ~P(E_{\text {rec}} | H_C) = 0.14,$
$P(E_{\text {rec}} | H_A) = 0.14,~ P(E_{\text {rec}} | H_B) = 0.005, ~P(E_{\text {rec}} | H_C) = 0.14,$
-
•
 $P(E_{\text {vm}} | H_A) = 0.05, ~P(E_{\text {vm}} | H_B) = 0.1,~ P(E_{\text {vm}} | H_C) = 0.6. $
$P(E_{\text {vm}} | H_A) = 0.05, ~P(E_{\text {vm}} | H_B) = 0.1,~ P(E_{\text {vm}} | H_C) = 0.6. $
3.3 Updating and Inference
The inferential (updating) process raises numerous questions for both the mathematical and narrative approaches. In the mathematical approach, the next step involves plugging our probabilities into Bayes’ rule. To compute the relative odds of two hypotheses across n pieces of evidence, Fairfield and Charman (Reference Fairfield and Charman2017, 373) instruct us to use the following equation:
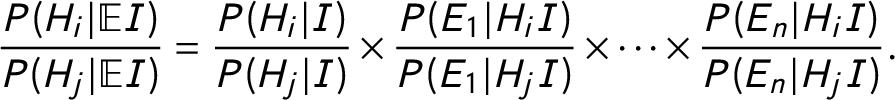 $$ \begin{align} \displaystyle\frac{P(H_i | \mathbb{E}I)}{P(H_j | \mathbb{E}I)} = \frac{P(H_i|I)}{P(H_j|I)} \times \frac{P(E_1|H_iI)}{P(E_1|H_jI)} \times \cdots \times \frac{P(E_n|H_iI)}{P(E_n|H_jI)}. \end{align} $$
$$ \begin{align} \displaystyle\frac{P(H_i | \mathbb{E}I)}{P(H_j | \mathbb{E}I)} = \frac{P(H_i|I)}{P(H_j|I)} \times \frac{P(E_1|H_iI)}{P(E_1|H_jI)} \times \cdots \times \frac{P(E_n|H_iI)}{P(E_n|H_jI)}. \end{align} $$
Using fairly conservative probabilities across the board, the final posterior estimates are shocking.Footnote
13
The probability Adam committed the murder alone is
![]() $P(H_A | \mathbb {E}I)$
= 0.077, the probability Bertrand committed the murder alone is
$P(H_A | \mathbb {E}I)$
= 0.077, the probability Bertrand committed the murder alone is
![]() $P(H_B | \mathbb {E}I)$
= 0.0008, and the probability Adam and Bertrand colluded in the specified way is
$P(H_B | \mathbb {E}I)$
= 0.0008, and the probability Adam and Bertrand colluded in the specified way is
![]() $P(H_C | \mathbb {E}I)$
= 0.922. In the face of such an ostensibly clear picture, we must ask, how sensitive are these results to the probabilities selected? Should researchers assess the sensitivity, and if so, how?Footnote
14
In terms of odds ratios, how close to 1 is too close to reliably conclude that evidence supports one hypothesis over another?
$P(H_C | \mathbb {E}I)$
= 0.922. In the face of such an ostensibly clear picture, we must ask, how sensitive are these results to the probabilities selected? Should researchers assess the sensitivity, and if so, how?Footnote
14
In terms of odds ratios, how close to 1 is too close to reliably conclude that evidence supports one hypothesis over another?
Conducting inference in the narrative approach raises even more fundamental questions. A core feature of Bayesianism is the iterative updating of our confidence in each hypothesis as we move through the evidence. These updates serve as weights for analyzing subsequent likelihoods. In more complex examples, researchers will have multiple pieces of evidence that inflate and attenuate our relative confidence in different pairwise comparisons of hypotheses. How do we incorporate weights (both informative and updated priors) into a narrative analysis? More broadly, how should researchers conducting narrative BPT keep track of which hypothesis is ahead of which other at each point in the analysis? At the risk of suggesting that we adopt good, plusgood, and doubleplusgood in earnest (Orwell Reference Orwell1949, 301), is there a ranking of language or a schema to help researchers move methodically through this analytic process?
The final question, of course, is “how good are our results?” If we step back and evaluate the quality of the output relative to the quality of the input, a frightening insight emerges. This analysis just led us to conclude—with 92% certainty—that two people colluded to murder someone. Yet, it is based entirely on circumstantial evidence. We have no evidence linking Adam to Bertrand, and none linking either to the actual crime. I argue that the singular focus on assessing the relative likelihood of evidence in one world versus another sets practitioners up to draw very certain conclusions on the basis of very thin evidence.
4 Discussion
I conclude with an evaluation of my experience using BPT and my final thoughts on the method itself. To start, I should be the ideal candidate for using BPT: I use and publish on process tracing, I have training in Bayesian statistics, and I believe the BPT scholars and I share the same core methodological values. Yet, I had extreme difficulty synthesizing disparate recommendations from the literature into a cohesive approach. I come away from this analysis with far more questions than I have answers and nowhere near the confidence in my conclusions that the numbers suggest I should have.Footnote 15 In short, the experience of using the method left me feeling as though it lacks both guidelines and guardrails.
Three persistent issues leave me still questioning whether the method can live up to its mission. First, I fear researchers could easily get so caught up in the technical process(es) of implementation that they overlook mediocre data and find themselves drawing much stronger and conclusions than they otherwise should (as I did above). Second, while scholars have repeatedly argued that the transparency of the BPT process means poor analytic choices will be subjected to scrutiny via peer review,Footnote 16 this assertion presumes reviewers will be fully conversant in the method. Yet, for applied work, most reviewers tend to be substantive experts, rather than methodologists. Finally, while some points have been clarified since I wrote “Updating Bayesian(s),” the literature still leaves many questions unanswered, relying instead on what should work in mathematical principle, rather than guiding what will likely happen in practice.
While BPT is not without its problems, I am not asking its proponents to dig their own grave either. If there were a method that could be implemented without bias or caution, I dare say we would never use anything else. I do ask, however, that any methodological literature equip future practitioners with (1) the tools needed to make informed choices about whether and how to implement the method, and (2) adequate warnings about where the method can go wrong and how. If the disconnect between principle and practice goes unresolved, the problems that follow are ones we all care to avoid: the loss of analytic transparency and, ultimately, bad inferences.
Supplementary Material
For supplementary material accompanying this paper, please visit https://doi.org/10.1017.pan.2021.24.

