2.1 The General WATE Estimand

Our discussion of the WATE estimand closely follows Li et al. (Reference Li, Morgan and Zaslavsky2018) who in turn build on work by Hirano et al. (Reference Hirano, Imbens and Ridder2003). We refer interested readers to these articles for more detailed discussion.

Consider a random sample of size n composed of independent and identically distributed draws from an infinite super-population:

$$ \begin{align*}\left\{ Y_i(0), Y_i(1), Z_i, X_i \right\}_{i=1}^n. \end{align*} $$

Here $Y_i(0)$ and $Y_i(1)$ are the potential outcomes for unit i under control and active treatment respectively, $Z_i$ is a binary treatment indicator with the convention that $Z_i=1$ indicates that unit i was exposed to active treatment and $Z_i=0$ indicates that unit i was exposed to the control condition, and $X_i = (X_{i1}, \ldots , X_{ik})$ are measured covariates specific to unit i. The observed outcome $Y_i$ is given by $Y_i = Z_i Y_i(1) + (1 - Z_i) Y_i(0)$ . See Imbens and Rubin (Reference Imbens and Rubin2015, Chapter 3) (2015). Finally, let $n^{(1)}$ and $n^{(0)}$ denote the number of treated and control units respectively.

The average treatment effect conditional on x is defined as:

$$ \begin{align*}\tau(x) \equiv \mathbb{E}\left[Y(1) - Y(0) | X=x \right]. \end{align*} $$

This is the average unit-specific causal effect among units with $X=x$ .

Although such conditional effects may be of direct interest in particular applications, the focus here is on weighted averages of these effects in the super-population. Assume that the density of X, $f_X(x)$ , exists.Footnote ³ Following Li et al. (Reference Li, Morgan and Zaslavsky2018, 392) and Hirano et al. (Reference Hirano, Imbens and Ridder2003,1163), define

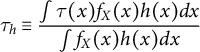(1) $$ \begin{align} \tau_h \equiv \frac{\int \tau(x) f_X(x) h(x) dx}{\int f_X(x) h(x) dx} \end{align} $$

to be the WATE. Here $h(x)$ is a weight function that defines the target population (i.e., the target population distribution is the super-population distribution weighted by $h(x)$ ) and the estimand. $\tau _h$ is simply a weighted average of covariate-specific conditional effects.

A wide range of commonly used causal estimands can be written as a WATE; the only difference is in the choice of the weight function $h(x)$ (Li et al. Reference Li, Morgan and Zaslavsky2018, 392). In this paper, we focus on ATE and ATT as they are the estimands most commonly used in political science. The ATE estimand corresponds to a situation where $h(x) = 1$ for all x and the ATT estimand corresponds to a situation where $h(x)$ is equal to the propensity score function, i.e., $h(x) = e(x) = \Pr (Z=1 | X=x)$ . That said, the ideas and diagnostics in this paper apply much more broadly.

2.2 A Hájek-Type Estimator of WATE

In this section, we describe a Hájek-type estimator of the WATE estimand and then note that many commonly used estimators of causal effects can be viewed as special cases of this weighting estimator. This provides the basis for comparing these estimators using the diagnostics discussed in Section 3.

The particular estimator that we focus on is the following:

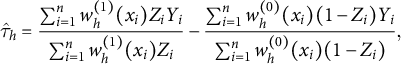(2) $$ \begin{align} \hat{\tau}_h = \frac{\sum_{i=1}^n w^{(1)}_{h}(x_i) Z_i Y_i}{\sum_{i=1}^n w^{(1)}_{h}(x_i) Z_i} - \frac{\sum_{i=1}^n w^{(0)}_{h}(x_i) (1-Z_i) Y_i}{\sum_{i=1}^n w^{(0)}_{h}(x_i) (1-Z_i)}, \end{align} $$

where $w^{(1)}_{h}(x)$ and $w^{(0)}_{h}(x)$ are weight functions for treated and control units respectively. This is based on the estimator proposed by Hájek (Reference Hájek, Godambe and Sprott1971) within the context of survey sampling. Accordingly, we refer to this as a Hájek-type estimator. This estimator goes by other names in the causal inference literature—most commonly stabilized IPW estimator (Aronow and Miller Reference Aronow and Miller2019, 228, 266).

Li et al. (Reference Li, Morgan and Zaslavsky2018) show that $\hat {\tau }_h$ is a consistent estimator of $\tau _h$ under the following conditions. Treatment assignment is conditionally ignorable given X, SUTVA holds,Footnote ⁴ and the weights are given by:

(3) $$ \begin{align} w^{(1)}_{h}(x) \propto \frac{f_X(x)h(x)}{f_X(x)e(x)} = \frac{h(x)}{e(x)}, \end{align} $$

and

(4) $$ \begin{align} w^{(0)}_{h}(x) \propto \frac{f_X(x)h(x)}{f_X(x)(1-e(x))} = \frac{h(x)}{1-e(x)}, \end{align} $$

where $e(x) = \Pr (Z=1 | X=x)$ is the propensity score function. As Li et al. (Reference Li, Morgan and Zaslavsky2018) also show, these weights have the property of balancing the covariates between treated and control groups such that these weighted conditional distributions are equal to each other and also equal to $f_X(x) h(x)$ (the covariate distribution of the target population):

(5) $$ \begin{align} f_{X|Z}(x|1) w^{(1)}_{h}(x) = f_{X|Z}(x|0) w^{(0)}_{h}(x) = f_X(x) h(x). \end{align} $$

While we have written the weights $w^{(1)}_{h}(x)$ and $w^{(0)}_{h}(x)$ as explicit functions of x, it will often be more notationally convenient to simply write them as values indexed by the units ( $i=1,\ldots ,n$ ). For example, as $w^{(1)}_{hi}$ and $w^{(0)}_{hi}$ or, when the estimand is clear by context, simply $w^{(1)}_{i}$ and $w^{(0)}_{i}$ .

2.3 Common Estimators are Equivalent to Hájek-Type Estimators

In this section, we briefly discuss the equivalences between a variety of estimators of ATE and ATT and the Hájek-type estimator discussed in the previous section. In some cases—for instance propensity score weighting methods and methods using balancing weights—these equivalences are obvious and well known within political science. In other cases—such as regression estimators of ATE and ATT—these equivalences have been proven in other fields but are not well known within political science. It is important to note that these are exact equivalences, not approximations.

2.3.1 Propensity Score Weighting Estimators

The group of estimators that can most obviously be written in the form of Equation (2) are those that directly estimateFootnote ⁵ the propensity score function $e(x)$ and then substitute that estimate, $\hat {e}(x)$ , into Equations (3) and (4). The general form of the resulting estimator is

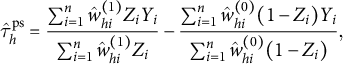(6) $$ \begin{align} \hat{\tau}^{\text{ps}}_h = \frac{\sum_{i=1}^n \hat{w}^{(1)}_{hi} Z_i Y_i}{\sum_{i=1}^n \hat{w}^{(1)}_{hi} Z_i} - \frac{\sum_{i=1}^n \hat{w}^{(0)}_{hi} (1-Z_i) Y_i}{\sum_{i=1}^n \hat{w}^{(0)}_{hi} (1-Z_i)}, \end{align} $$

where

$$ \begin{align*}\hat{w}^{(1)}_{hi} = \frac{h(x_i)}{\hat{e}(x_i)}, \end{align*} $$

$$ \begin{align*}\hat{w}^{(0)}_{hi} = \frac{h(x_i)}{1-\hat{e}(x_i)}. \end{align*} $$

When $h(x)$ for the estimand in question depends on $e(x)$ , the estimate $\hat {e}(x)$ is substituted into the expression for $h(x)$ as well. Both ATE and ATT can be consistently estimated with this approach. As noted above, the ATE estimand has $h(x) = 1$ for all x. For the ATT estimand, $h(x) = e(x)$ so we set $\hat {h}(x) = \hat {e}(x)$ . This produces the following weights:

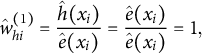$$ \begin{align*}\hat{w}^{(1)}_{hi} =\frac{\hat{h}(x_i)}{\hat{e}(x_i)} = \frac{\hat{e}(x_i)}{\hat{e}(x_i)} = 1, \end{align*} $$

and

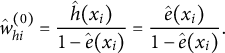$$ \begin{align*}\hat{w}^{(0)}_{hi} = \frac{\hat{h}(x_i)}{1-\hat{e}(x_i)} = \frac{\hat{e}(x_i)}{1-\hat{e}(x_i)}. \end{align*} $$

2.3.2 Methods Using Balancing Weights

Another group of estimators approach the selection of weights for Equation (2) as an explicit constrained optimization problem. We refer to these estimators as balancing weights estimators (for examples of such estimators, see Hainmueller Reference Hainmueller2012; Hazlett Reference Hazlett2020; Wang and Zubizarreta Reference Wang and Zubizarreta2020; Zubizarreta Reference Zubizarreta2015). The approaches differ in how they define the optimization problem, but in general they attempt to find weights that create (at least) approximate balance between treated and control groups subject to constraints. That is, the weights they find equate the weighted covariate distribution among the treated units with the weighted covariate distribution among the control units as in Equation (5).

These approaches are most often used to estimate the ATT, which is typically written as:

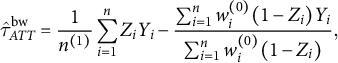$$ \begin{align*}\hat{\tau}^{\text{bw}}_{ATT} = \frac{1}{n^{(1)}} \sum_{i=1}^n Z_i Y_i - \frac{\sum_{i=1}^n w^{(0)}_i (1 - Z_i) Y_i}{ \sum_{i=1}^n w^{(0)}_i (1 - Z_i) }, \end{align*} $$

where $n^{(1)} = \sum _{i=1}^n Z_i$ and $w^{(0)}_i \ \ i=1,\ldots ,n$ are weights chosen to maximize balance between the treated and control groups subject to constraints. It is obvious that this expression for $\hat {\tau }^{\text {bw}}_{ATT}$ is a special case of the WATE estimator in Equation (2).Footnote ⁶

2.3.3 Regression Estimators

In an important recent work, Chattopadhyay and Zubizarreta (Reference Chattopadhyay and Zubizarreta2023) have shown that regression estimators of ATE and ATT are also equivalent to the Hájek-type estimator in Equation (2).Footnote ⁷ This important fact is not widely known within political science.

The Multi-Regression Imputation (MRI) Estimator. To begin, consider the following regression estimator for ATE:

(7) $$ \begin{align} \hat{\tau}^{\text{reg}}_{ATE} = \frac{1}{n} \sum_{i=1}^n \left(\hat{m}_1(x_i) - \hat{m}_0(x_i)\right) \end{align} $$

where $\hat {m}_1(x)$ is the ordinary least squares (OLS) regression estimator of $\mathbb {E}[Y | X=x, Z=1]$ constructed by subsetting the data to the $Z=1$ units and fitting an OLS regression of Y on X to those data and $\hat {m}_0(x)$ is the OLS regression estimator of $\mathbb {E}[Y | X=x, Z=0]$ constructed by subsetting the data to the $Z=0$ units and fitting an OLS regression of Y on X to those data. Chattopadhyay and Zubizarreta (Reference Chattopadhyay and Zubizarreta2023) refer to this as the MRI estimator of ATE.Footnote ⁸

Let $\mathbf {X}$ denote the $n \times (k+1)$ matrix of covariates including a constant. Similarly, let $\mathbf {X}_1$ and $\mathbf {X}_0$ denote the submatrices that correspond to the portions of $\mathbf {X}$ from the treated and control units respectively. The treatment indicator, Z, is not included in $\mathbf {X}$ , $\mathbf {X}_0$ , or $\mathbf {X}_1$ . Relatedly, let $\mathbf {y}$ denote the $n \times 1$ vector of outcomes for the full sample and $\mathbf {y}_1$ and $\mathbf {y}_0$ be the observed outcomes for the treated and control units respectively.

The regression estimator in Equation (7) is equivalent to the Hájek-type estimator in Equation (2) where the weights applied to the treated units are $\mathbf {w}^{(1)'} = \mathbf {1}^{\prime }_n \mathbf {X} \left ( \mathbf {X}_1^{\prime } \mathbf {X}_1\right )^{-1} \mathbf {X}_1^{\prime } $ and the weights applied to the control units are $\mathbf {w}^{(0)'} = \mathbf {1}_n^{\prime } \mathbf {X} \left ( \mathbf {X}_0^{\prime } \mathbf {X}_0\right )^{-1} \mathbf {X}_0^{\prime } $ (Chattopadhyay and Zubizarreta Reference Chattopadhyay and Zubizarreta2023).Footnote ⁹ Here $\mathbf {1}_n$ is an n-vector of ones. Note that these weights can be negative.Footnote ¹⁰ To get some intuition about these weights, note that the imputed treated outcomes are given by

$$ \begin{align*}\hat{\mathbf{m}}_1(\mathbf{X}) = \mathbf{X} \hat{\boldsymbol{\beta}}_1 = \mathbf{X} (\mathbf{X}_1^{\prime}\mathbf{X}_1)^{-1}\mathbf{X}_1^{\prime}\mathbf{y}_1 \end{align*} $$

which is a weighted average of the outcomes for the treated units. The imputed control outcomes are constructed similarly.

Closely related arguments to those above for ATE can be used to express the following MRI estimator of ATT:

$$ \begin{align*}\hat{\tau}^{\text{reg}}_{ATT} = \frac{1}{n^{(1)}} \sum_{i:Z_i=1} \left(y_i - \hat{m}_0(x_i)\right) \end{align*} $$

in the form of Equation (2) (Chattopadhyay and Zubizarreta Reference Chattopadhyay and Zubizarreta2023).Footnote ¹¹

The Uni-Regression Imputation (URI) Estimator One may also attempt to estimate an average treatment effect with a single regression. Let $\mathbf {z}$ be the $n \times 1$ vector of treatment indicators. Then, as shown by Chattopadhyay and Zubizarreta (Reference Chattopadhyay and Zubizarreta2023), the commonly used OLS estimator of $\tau $ in the regression $\mathbf {y} = \mathbf {X} \boldsymbol {\beta } + \mathbf {z} \tau + \boldsymbol {\epsilon }$ (what Chattopadhyay and Zubizarreta (Reference Chattopadhyay and Zubizarreta2023) refer to as the URI estimator) is equivalent to the Hájek-type estimator of Equation (2) with a particular choice of weights (Chattopadhyay and Zubizarreta Reference Chattopadhyay and Zubizarreta2023). See also Section B of the Supplementary Material for an alternative derivation of these weights and discussion of their properties.Footnote ¹² See Hazlett and Shinkre (Reference Hazlett and Shinkre2024) for a discussion of the URI estimator and its drawbacks compared to other estimators (including the MRI estimator).

Bivariate Weighted Least Squares (WLS) on the Treatment Indicator. A third approach using regression is primarily of interest to us because it underlies our DFBETA diagnostic of Section 3.2. As Imbens (Reference Imbens2004) notes, the Hájek-type estimator of $\hat {\tau }_h$ in Equation (2) is equivalent to the WLS estimator of $\tau _h$ in the following bivariate regression of the observed outcomes on the treatment indicator:

(8) $$ \begin{align} Y_i = \beta_0 + Z_i \tau_h + \epsilon_i, \ \ \ \ i=1,\ldots,n \end{align} $$

with the ith regression weight equal to:

$$ \begin{align*}\omega_i = Z_i w^{(1)}_{h}(x_i) + (1-Z_i) w^{(0)}_{h}(x_i). \end{align*} $$

As Section 3.2 shows, this equivalence enables us to use standard regression diagnostics to understand the influence of particular observations on any Hájek-type estimate of a WATE—even those that do not explicitly model the outcome via regression (e.g., entropy balancing estimates).Footnote ¹³

3.1 Effective Sample Size & Effective Sample Size Ratio

In the survey sampling literature, it is common place to calculate and report the “effective sample size” of a weighted estimator (Kish Reference Kish1965). The basic idea is to note the variance of the unweighted sample mean, $\bar {Y}$ , of Y is $\mathbb {V}[\bar {Y}] = \mathbb {V}[Y]/n$ where n is the sample size. If the variance of a weighted estimator can be written as $ \mathbb {V}[Y]/c$ for some constant c, then the effective sample size is c. While $\mathbb {V}[Y]$ appears in this motivation, the effective sample size can be calculated before outcome data is collected. We return to this point at the end of this subsection.

The Hájek-type estimator in Equation (2) depends on the weights $w_{hi}^{(1)}$ and $w_{hi}^{(0)}$ . Thus the effective sample size of this estimator will also depend on these weights. To acknowledge that, we use the notation $n_{\text {eff}_w} $ to denote the effective sample size of this estimator.

Under the assumption that $\mathbb {V}[Y|Z=1] = \mathbb {V}[Y|Z=0] = \mathbb {V}[Y]$ , some simple variance calculations and algebraic manipulations give us the following expression for $n_{\text {eff}_w} $ (see Section D of the Supplementary Material)Footnote ¹⁷ :

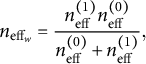$$ \begin{align*}n_{\text{eff}_w} = \frac {n^{(1)}_{\text{eff}} n^{(0)}_{\text{eff}}}{ n^{(0)}_{\text{eff}} + n^{(1)}_{\text{eff}}}, \end{align*} $$

where

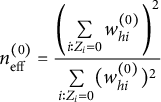$$ \begin{align*}n^{(0)}_{\text{eff}} = \frac {\left(\sum\limits_{i:Z_i=0}w^{(0)}_{hi}\right)^2}{\sum\limits_{i:Z_i=0}(w^{(0)}_{hi})^2} \end{align*} $$

and

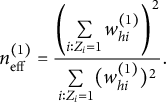$$ \begin{align*}n^{(1)}_{\text{eff}} = \frac {\left(\sum\limits_{i:Z_i=1}w^{(1)}_{hi}\right)^2}{\sum\limits_{i:Z_i=1}(w^{(1)}_{hi})^2}. \end{align*} $$

If the weights are estimated, these estimated weights can be inserted into the above formulas in place of $w_{hi}^{(1)}$ and $w_{hi}^{(0)}$ . If at least one $w_{hi}^{(1)}$ value is non-zero and one $w_{hi}^{(0)}$ value is non-zero, then

$$ \begin{align*} 0 < n^{(0)}_{\text{eff}} \le n^{(0)} \end{align*} $$

$$ \begin{align*} 0 < n^{(1)}_{\text{eff}} \le n^{(1)} \end{align*} $$

and

$$ \begin{align*} 0 < n_{\text{eff}_w} \le \frac{n^{(1)} n^{(0)}}{n^{(0)} + n^{(1)}} \le n/4. \end{align*} $$

Full details are presented in Section D of the Supplementary Material.

The effective sample size is most useful when comparing two or more estimators. It is also useful to express the effective sample size as a fraction of the maximum possible effective sample size, $\frac {n^{(1)} n^{(0)}}{n^{(0)} + n^{(1)}}$ , or what we term the effective sample size ratio. The applications in Section 4 provide examples.

Since the weights for all of the estimators considered in this paper do not depend on the outcome data, the effective sample size can be calculated prior to observing or recording any outcome data. This is especially relevant in situations where researchers may want to adjust model specifications based on diagnostic information. Making such adjustments prior to observing outcome information minimizes the chance of bias from researcher degrees of freedom (Rubin Reference Rubin2008).

3.2 Influential Data Points

Understanding the extent to which some observations may exert a great deal of influence over one’s estimates is an important part of any data analysis. Conceptually, one can gauge the influence of observation i by examining the difference between an estimate calculated with the full dataset and an estimate calculated with observation i removed. Ideally, one would like a closed form expression for this measure of influence, as repeatedly deleting observations and re-estimating the quantity of interest can be extremely time-consuming with large datasets and sophisticated estimation methods.

Chattopadhyay and Zubizarreta (Reference Chattopadhyay and Zubizarreta2023) have made progress on this goal for the MRI and URI estimators discussed above. What they term the sample influence curve for observation i (denoted $\text {SIC}_i$ ) is proportional to this difference in estimates with and without observation i.Footnote ¹⁸ While this provides an exact measure of influence for URI and MRI estimates of ATE, it is not directly useful for non-regression estimates of ATE.

We provide a measure of influence that works for any estimator that can be written as the Hájek-type estimator of Equation (2).

Recall from Section 2.3.3 that any Hájek-type estimator of the form given in Equation (2) is equivalent to a bivariate WLS regression of the outcome on the treatment indicator. Since the coefficient on the treatment indicator in this bivariate WLS regression is the causal effect of interest, a measure of how much this coefficient changes after deleting observation i is a measure of influence that will work for any Hájek-type estimator. In the literature on regression diagnostics, this change in a coefficient vector after deleting observation i is referred to as DFBETA $_i$ (Belsley, Kuh, and Welsch Reference Belsley, Kuh and Welsch1980) and is closely related to the approach of Chattopadhyay and Zubizarreta (Reference Chattopadhyay and Zubizarreta2023) for URI and MRI estimators.

Directly relevant to our goal of finding a closed form expression for DFBETA $_i$ for WLS regression is the work of Li and Valliant (Reference Li and Valliant2011) who studied the analogous problem of calculating DFBETA $_i$ in regressions with survey weights. Their work provides a closed form expression for DFBETA $_i$ for WLS regression. We use this to assess the influence of each observation on the Hájek-type estimator in Equation (2).Footnote ¹⁹ Note that we are interested in the second element of DFBETA $_i$ from the bivariate WLS regression as it reveals how much the causal effect estimate would change if observation i were deleted. Full details of how DFBETA $_i$ can be calculated for any Hájek-type estimator are presented is Section E of the Supplementary Material.

3.3 Extrapolation

A key question to ask when using either a URI or MRI estimator to estimate a causal effect is “Are any of the elements of $\mathbf {w}^{(1)}$ or $\mathbf {w}^{(0)}$ negative?”Footnote ²⁰ If all of the weights are non-negative, then each of the two weighted averages on the right-hand side of Equation (2) will be a convex combination of the observed treated and control outcomes respectively. In other words, the estimator is interpolating the observed data. If some of the weights are negative, then the estimator is extrapolating outside the range of the observed data.Footnote ^{21 ,} Footnote ²²

Although researchers should be concerned about any amount of extrapolation, the dangers of extrapolation vary with the extremity of the extrapolation. A simple measure of the amount of extrapolation in the estimation of the mean of $Y(0)$ is

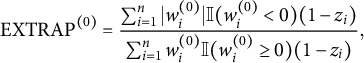$$ \begin{align*}\text{EXTRAP}^{(0)} = \frac{\sum_{i=1}^n |w_i^{(0)}|\mathbb{I}(w_i^{(0)} < 0) (1 - z_i)}{\sum_{i=1}^n w_i^{(0)} \mathbb{I}(w_i^{(0)} \ge 0) (1 - z_i)}, \end{align*} $$

where $\mathbb {I}(\cdot )$ is the indicator function and $|\cdot |$ is the absolute value function. EXTRAP $^{(0)}$ is the ratio of the sum negative control group weights to the sum of the positive control group weights. The amount of extrapolation in the estimation of the mean of $Y(1)$ is defined analogously as:

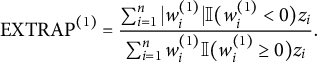$$ \begin{align*}\text{EXTRAP}^{(1)} = \frac{\sum_{i=1}^n |w_i^{(1)}|\mathbb{I}(w_i^{(1)} < 0) z_i}{\sum_{i=1}^n w_i^{(1)} \mathbb{I}(w_i^{(1)} \ge 0) z_i}. \end{align*} $$

For the regression estimators discussed in Section 2.3.3 EXTRAP $^{(0)}$ and EXTRAP $^{(1)}$ take values between 0 and 1.Footnote ²³ See Section B.2 of the Supplementary Material for details.

3.4 Balance

We can assess balance between the treated and control groups by weighting the covariate distributions within the treated and control groups by $w_h^{(1)}(x)$ and $w_h^{(0)}(x)$ respectively and checking to see whether Equation (5) holds in the sample.Footnote ²⁴ There are two broad approaches to this. The first checks whether the weighted means of the distributions in Equation (5) are equal. The second attempts to assess the overall equality of these distributions.Footnote ²⁵

3.4.1 Weighted Mean Balance

A standard measure of balance is the absolute standardized mean difference (ASMD). Following Chattopadhyay et al. (Reference Chattopadhyay, Hase and Zubizarreta2020) this is defined for a particular covariate x as:

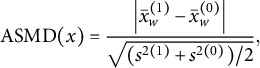$$ \begin{align*}\text{ASMD}(x) = \frac{\left| \bar{x}_w^{(1)} - \bar{x}_w^{(0)} \right|}{\sqrt{ ( s^{2(1)} + s^{2(0)} ) / 2} }, \end{align*} $$

where

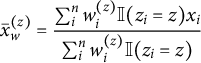$$ \begin{align*}\bar{x}_w^{(z)} = \frac{\sum_i^n w_i^{(z)} \mathbb{I}(z_i = z) x_i }{ \sum_i^n w_i^{(z)} \mathbb{I}(z_i = z)} \end{align*} $$

is the weighted mean of covariate x within treatment group z with weights given by $\mathbf {w}^{(z)}$ and $s^{2(z)}$ is the sample variance of x within treatment group z. See also Imbens and Rubin (Reference Imbens and Rubin2015, 310, 311) (2015, pp. 310–311) who propose using the standardized mean difference to check balance.

Chattopadhyay et al. (Reference Chattopadhyay, Hase and Zubizarreta2020) also propose using the target ASMD (TASMD) as a measure of balance. For a particular covariate x within treatment group z (denoted $x^{(z)}$ ), this is defined as:

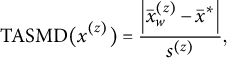$$ \begin{align*}\text{TASMD}(x^{(z)}) = \frac{\left| \bar{x}_w^{(z)} - \bar{x}^{*} \right|}{s^{(z)}}, \end{align*} $$

where $ \bar {x}_w^{(z)}$ is as above (the weighted mean of $x^{(z)}$ with weights given by $\mathbf {w}^{(z)}$ ), $\bar {x}^{*}$ is the sample mean of x within the target population, and $s^{(z)}$ is the unweighted sample standard deviation of x within treatment group z. The target population is simply the population that defines the estimand. For instance, if the estimand is ATE, then the target population weights each observation in the sample equally and $\bar {x}^{*}$ is the simple sample mean of x. If the estimand is ATT, then $\bar {x}^{*}$ is the simple sample mean of x within the treated units. With binary treatment, one would calculate TASMD $(x^{(0)})$ and TASMD $(x^{(1)})$ unless one of these quantities is trivially equal to 0 as with ATT.

Recall the balance condition from Equation (5):

$$ \begin{align*}f_{X|Z}(x|1) w^{(1)}_{h}(x) = f_{X|Z}(x|0) w^{(0)}_{h}(x) = f_X(x) h(x). \end{align*} $$

ASMD assesses the first equality, $f_{X|Z}(x|1) w^{(1)}_{h}(x) = f_{X|Z}(x|0) w^{(0)}_{h}(x)$ , whereas TASMD assesses $ f_{X|Z}(x|1) w^{(1)}_{h}(x) = f_X(x) h(x) $ and $ f_{X|Z}(x|0) w^{(0)}_{h}(x) = f_X(x) h(x) $ .

It is common to use an arbitrary threshold to assess weighted mean covariate balance. For instance, values of ASMD and/or TASMD below 0.1 or 0.2 are often viewed as indicating adequate covariate balance (Chattopadhyay et al. Reference Chattopadhyay, Hase and Zubizarreta2020, 15). Rather than using these arbitrary thresholds, Chattopadhyay et al. Reference Chattopadhyay, Hase and Zubizarreta2020 recommend using an asymptotically informed threshold of $\min (0.1, k^{- \frac {1}{2}} )$ , where k is the number of covariates (including functions of covariates such as squared terms) that one is attempting to balance (p. 15).

A major advantage of ASMD and TASMD is that they are not affected by sample size as a z-statistic or t-statistic would be (Imai, King, and Stuart Reference Imai, King and Stuart2008; Imbens and Rubin Reference Imbens and Rubin2015). A disadvantage is that they only assess mean balance and situations can exist where mean balance is achieved but confounding still exists because of imbalance on higher moments of the covariate distribution.

As proven by Chattopadhyay and Zubizarreta (Reference Chattopadhyay and Zubizarreta2023), the MRI estimators of ATE and ATT and the URI estimator of ATE will, by construction, always produce perfect weighted mean balance (both in terms of of ASMD and TASMD) on covariates included in the regression model(s)(Chattopadhyay and Zubizarreta Reference Chattopadhyay and Zubizarreta2023, Proposition 3). As they note, this implies that it is important to check balance on covariates—and transformations of covariates—that were not included in the model(s).Footnote ²⁶ Another way to view the fact that the MRI and URI estimators produce perfect weighted mean balance is that either weighted mean balance is less important than commonly thought or that regression estimators of ATE and ATT are better than commonly thought.

We agree, and we encourage practitioners to go even further to assess more general distributional balance rather than just weighted mean balance. In the next subsection we discuss two approaches can be used to assess more general distributional equality of covariates, beyond simple mean balance, across treated and control groups.

4.1 Promotion-Seeking Judges

Black and Owens (Reference Black and Owens2016) ask whether U.S. lower-court judges are more likely to cast votes in favor of the president when a vacancy exists on the U.S. Supreme Court.Footnote ²⁹ The researchers hypothesize that judges with a chance of promotion to the U.S. Supreme Court (“contenders”) are more likely to favor the president when a vacancy exists than when a vacancy does not exist. “Non-contenders” (judges with no chance of promotion) are not expected to adjust their votes in response to a vacancy. In other words, Black and Owens (Reference Black and Owens2016) frame their main research question as a causal question: What is the causal effect of a Supreme Court vacancy on pro-president votes cast by judges who are contenders and by judges who are not contenders?

Black and Owens’s approach to answering this question is typical of much applied work. They calculate and report a single estimate of a single causal estimand (in their case, an estimate of ATT produced by CEM).Footnote ³⁰ And that estimate supports their hypothesis: the treatment (a vacancy) causes contender judges to vote differently—such that when a vacancy exists, contenders are more likely to vote for the president to improve their promotion prospects, while non-contenders do not change their behavior.

We re-analyze the Black and Owens data using multiple estimators of ATT and report the results in Table 1.

Table 1 Re-analysis of Black and Owens (Reference Black and Owens2016) with multiple approaches to estimating the ATT.

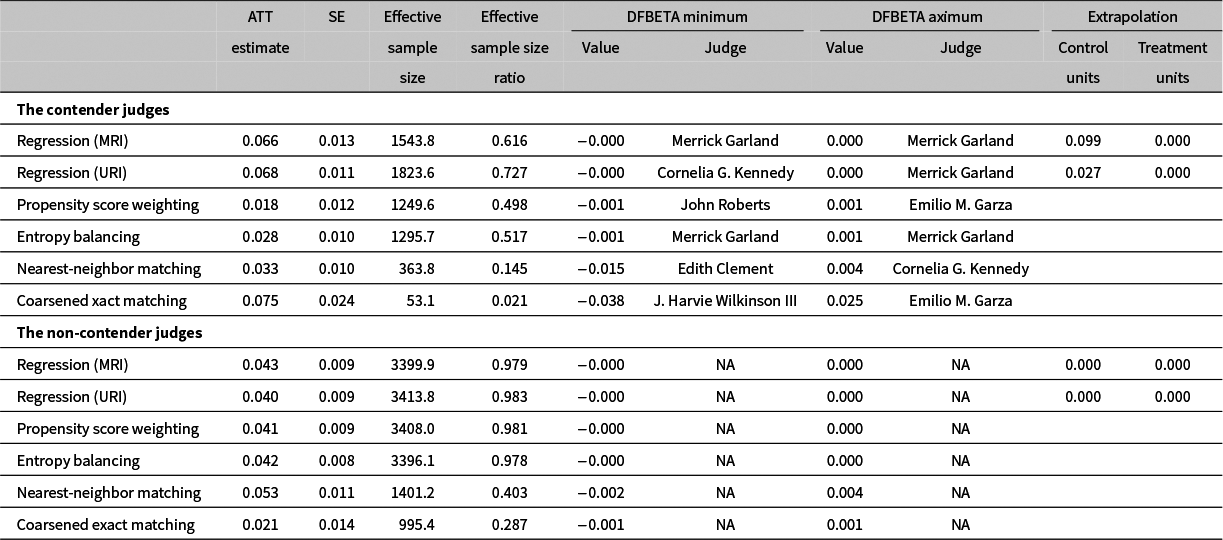
Note: The Regression (MRI) rows correspond to the MRI estimator of ATT. The Regression (URI) rows correspond to the URI estimator which is also an estimate of ATE under the constant effects assumption. The Propensity Score Weighting rows correspond to the propensity score weighting estimator of ATT in which the propensity scores are estimated via logistic regression. The Entropy Balancing rows correspond to the entropy balancing estimator of ATT as implemented in the WeightIt R package. The Nearest-Neighbor Matching rows correspond to 1:1 nearest neighbor propensity score matching using the Match function in the Matching R package and the same estimated propensity scores as above. The Coarsened Exact Matching rows correspond to the coarsened exact matching estimator of ATT as implemented in the cem R package. The minimum and maximum DFBETA values actually correspond to votes by particular judges on particular cases (the units in the study). The listed judge names are the names of the judges from those influential judge-case combinations. Judge names were not reported in the non-contender dataset.

Looking at the ATT estimates and associated standard errors in the CEM rows of Table 1, we see support for Black and Owens hypotheses. The ATT estimate for contenders is positive (0.075) and significant at conventional levels ( $z= 0.075/0.024 = 3.125$ ), while the ATT estimate for non-contenders is not significantly different from 0 at conventional levels ( $z = 0.021 / 0.014 = 1.5$ ). Taken at face value, these results suggest that contenders change their voting behavior in the expected pro-president direction when a Supreme Court vacancy arises, but non-contenders do not change their behavior in these circumstances.

Then again, questions about the credibility of this result emerge if one follows our guidance and examines the diagnostics for several estimators of ATT.

We begin by examing the diagnostics for Black and Owens’ preferred CEM estimator. Although Black and Owens (Reference Black and Owens2016, 36) report a sample size of 11,787 contender-judge observations,Footnote ³¹ note that the effective sample size for the contender analysis is 53.1 and the effective sample size ratio is 0.021—meaning that their CEM analysis discards approximately 98% of the possible data for the contenders. The CEM analysis of the non-contender judges also discards a fair amount of data but the effective sample size ratio is not as low as it is for contender judges.

In addition, the DFBETA values for the CEM analysis of the contender judges reveal that some judge-votes exert a very large influence on the estimated effect. The negative DFBETA with the largest magnitude belongs to a vote by Judge J. Harvie Wilkinson III and is equal to $-0.038$ . Dropping this vote by Judge Wilkinson would have increased the estimate of ATT by approximately 50%.Footnote ³² The largest positive DFBETA is equal to 0.025 and is from a vote by Judge Emilio Garza. The inclusion of this vote by Judge Garza produces approximately one third of the total estimated effect.Footnote ³³

Taken on their own, these diagnostics applied to the CEM analysis provide cause for questioning whether the data support Black and Owens’s hypotheses about contender judges. Even more red flags go up when we examine the diagnostics for the other methods of estimating ATT (all of which are based on the same causal identification assumptions of SUTVA and conditional ignorability of treatment assignment given the same covariates).

Looking at Table 1 we see that the other estimation methods all have much larger effective sample sizes, and smaller DFBETA values for contender judges than does CEM. The regression methods do result in some extrapolation for the contender judges, which would be a reason to prefer another estimation method.

We also investigate the covariate balance produced by all of these estimation methods. Figure 1 presents diagnostic plots for contender judges.Footnote ³⁴ Specifically, Figure 1a plots the TASMD values and Figure 1b the weighted KS statistics, both for control units. Recall that for a particular estimation method and covariate, the TASMD value and for the controls is the standardized absolute difference between the weighted mean of the covariate within the control observations (with weights given by $w_h^{(0)}(x)$ ) and the mean of that covariate in the target distribution. Because the estimand in this example is the ATT, the covariate means under the target distribution are just the sample means of the covariates within the set of all treated units.

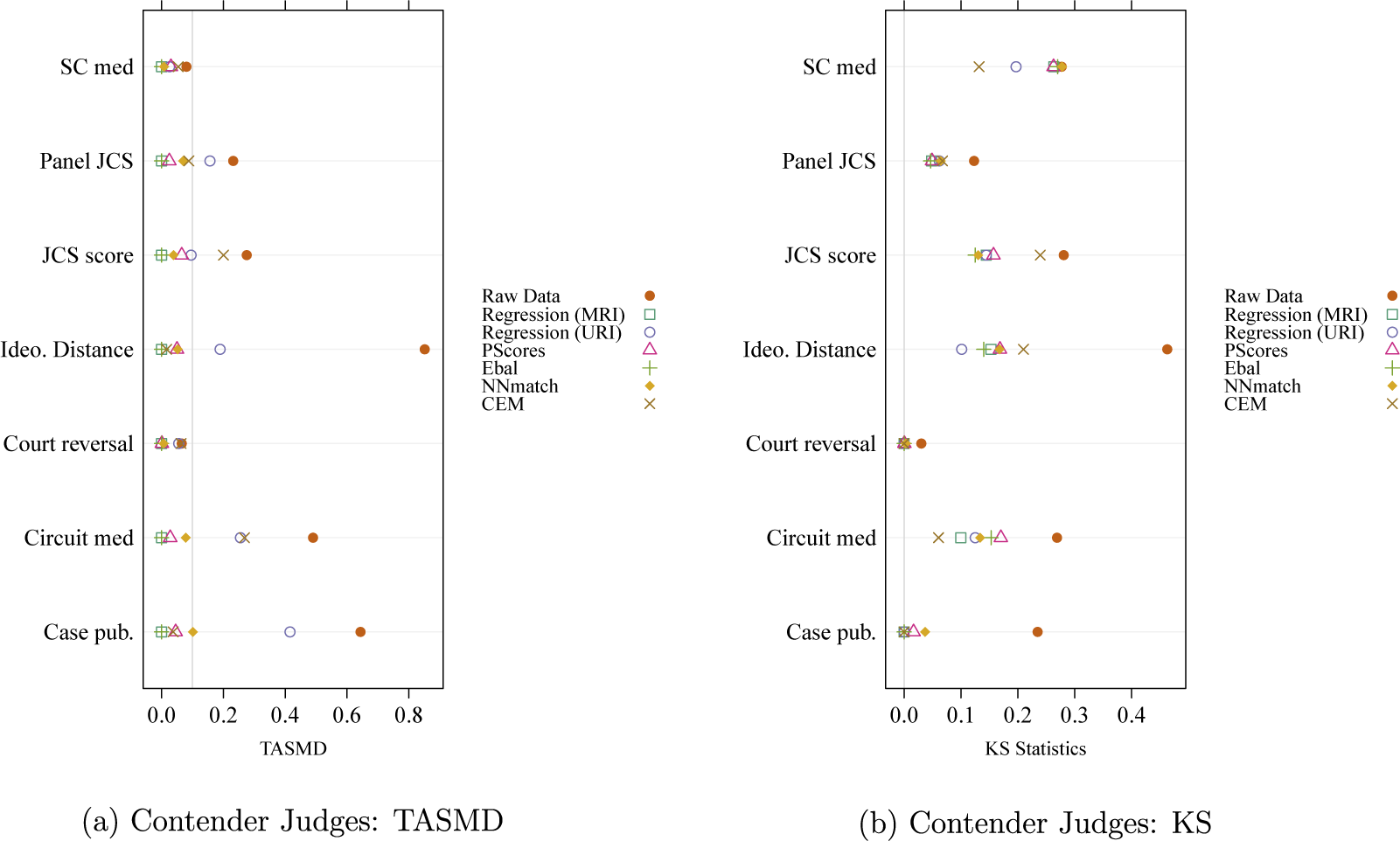
Figure 1 Weighted mean covariate balance (assessed by TASMD) and KS test statistic for control units using multiple ATT estimation methods in the re-analysis of Black and Owens (Reference Black and Owens2016).

Note: In the TASMD plot, each symbol shows the standardized difference between the weighted mean of the control and treated data for each covariate and method. The gray vertical line marks where the TASMD value is 0.1. In the KS statistic plot, each symbol shows the maximum absolute difference in the ECDFs of the control and treated groups, using both raw and weighted control data. The gray vertical line marks KS statistics at 0. SC med is the JCS score of the median Supreme Court justice; Panel JCS is the ideological distance between a judge and the remaining panelists; JCS score is each judge’s JCS score; Ideo. Distance is the ideological distance between the judge and the president; Court reversal is whether the circuit court reversed the lower court; Circuit med is the JCS score of the median judge on the circuit; and Case pub. is whether the case was published.

Looking at Figure 1a, we see that the non-CEM methods, with the exception of the URI estimator, all produce good to very good balance as evidenced by TASMD values below 0.2 and in most cases below 0.1. The MRI estimator of ATT, the propensity score weighting estimator of ATT, and the entropy balancing estimator of ATT produce especially good balance—although it is important to note that the MRI estimator achieves this balance with negative weights, i.e., via extrapolation.Footnote ³⁵

Similarly, the weighted KS test statistics compare the weighted distribution of control units to the target distribution, which is the treated group in this case. KS statistics indicate the maximum absolute difference between the empirical cumulative distribution functions (ECDFs) of the two distributions. As a normalized measure, the distance ranges from 0 (identical distributions) to 1 (completely different distributions). Figure 1b plots the KS test statistics for the covariates, comparing raw and weighted control units and treated groups. As we see, almost all methods reduce the KS statistics compared to the raw data, thereby improving distributional balance.

The comparison in Figure 1 clarifies how different methods handle data at hand and provides guidance for examining specific covariate of interest. For example, Ideo. Distance measures ideological distance between the judge and the president, is an important confounder given the research question. Figure 1 shows the unweighted control and the treated group exhibit poor mean and distributional balance. Among all methods, entropy balancing performs the best in achieving both mean and distributional balance.Footnote ³⁶

Looking at the various weighted QQ-plots for these covariates helps to clarify how balance is being improved. Given space limitations, we present a single weighted QQ-plot for the Ideo. Distance covariate among contender judges in Figure 2. Here we see that in the raw data, Ideo. Distance is quite different among treated and control units. Entropy-balancing weights help to shrink this difference. That said, differences on this covariate between treated and control units remain after applying the entropy-balancing weights. While one might favor the entropy balancing results over the other results, one might also wonder whether any of the estimation approaches provide sufficient control of confounding.

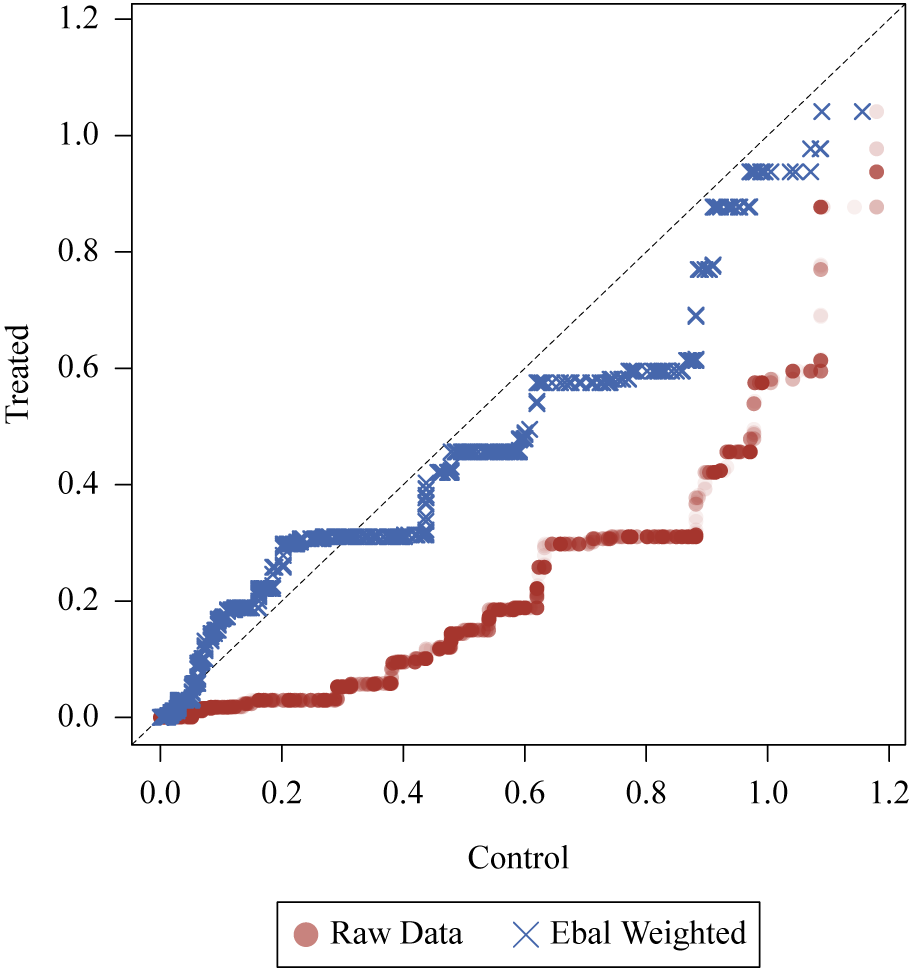
Figure 2 Quantile-quantile plot for Ideo. Distance with raw and entropy-balancing-weighted data for contender judges.

Note: The X-axis depicts weighted quantiles of ideological distance between the judge and the president for the control units, while the Y-axis shows depicts weighted quantiles of ideological distance for the treated group, which is the target distribution in this case. A point on the 45-degree line indicates equality of the quantiles represented by that point.

Given these diagnostics, it seems that the estimation approaches with the fewest obvious problems (as revealed by the diagnostics) are propensity score weighting and entropy balancing. If these approaches produced results that were consistent with Black and Owens’ hypothesis of promotion-seeking behavior among judges, then we might conclude that the overall takeaway from Black and Owens (Reference Black and Owens2016) is correct, even if the estimation method they preferred in that paper doesn’t work well in that application. Going back to Table 1, we see that this is not the case. Neither the propensity score weighting nor the entropy balancing estimates show that contenders respond differently to a vacancy than do non-contenders. If anything, the point estimates from propensity score weighting and entropy balancing (as well as nearest-neighbor matching) are actually larger for the non-contenders than for the contenders (though none of the differences are statistically significant).

To conclude, based on Table 1 and Figure 1, when it comes to estimating ATT for contender judges, propensity score weighting and entropy balancing are better choices than the default application of CEMFootnote ³⁷ for this application. At the least, these approaches use the data more efficiently, do not generate extreme influential data points, do not extrapolate, and produce good covariate balance. Unfortunately, though, neither propensity score weighting nor entropy balancing produces results that support the authors’ hypotheses. For the contenders, the causal effect of a vacancy on voting is not statistically different from 0 based on the propensity score weighting estimator and substantively fairly trivial based on the entropy balancing estimate. As for the non-contenders, there is evidence that a vacancy exerts a small, significant effect on voting behavior—against the authors’ expectation.

4.2 Wealth-Maximizing Politicians

In our second applied example, we turn to a study by Eggers and Hainmueller (Reference Eggers and Hainmueller2009). They ask whether members of the British parliament, relative to losing parliamentary candidates, accumulate greater wealth. Or, more succinctly: What is the causal effect of serving in parliament on wealth accumulation? The authors provide theoretical reasons to think that the effect of office on wealth accumulation differs for Conservative MPs compared to Labour MPs and so condition their analysis on party.

In contrast to Black and Owens (Reference Black and Owens2016), Eggers and Hainmueller (Reference Eggers and Hainmueller2009) report estimates of three different causal estimands (ATE, ATT, and the local average effect from a regression discontinuity design); and they also make use of three different estimation methods (OLS regression, difference of means after 1:1 genetic matching with replacement, and local regression for the regression discontinuity estimates). Although small differences emerge across these various methods, the main substantive point is remarkably consistent: Holding office has a substantial, positive effect on the wealth of Conservative MPs, whereas “no discernible financial benefits [accrue] for Labour MPs” (Eggers and Hainmueller Reference Eggers and Hainmueller2009, 513).

Considering the stability of Eggers and Hainmueller’s results, it would seem that our proposed diagnostics would add little value to their work. And, in fact, our tools supply no cause to question Eggers and Hainmueller’s general substantive conclusions. But they do clarify how various methods use the data at hand and which observations (MPs) exert substantial influence on the reported results. So even in this application, which is close to current “best practices,” our diagnostics may still aid researchers and their readers by shedding new light on the analyses and aiding proper interpretation of the findings.

For purposes of illustrating the diagnostics discussed above, we focus, in Table 2, on the ATT and ATE for Conservative Party politicians (see also Section G of the Supplementary Material). Looking at this table we see that the two regression approaches (MRI and URI) tend to have relatively large effective sample sizes and the most influential observations under these methods exert no more influence on the results than the most influential observations under other methods. These regression methods do extrapolate to some extent which could be a reason to prefer other methods. That said, the amount of extrapolation is relatively small.

Table 2 Re-analysis of Eggers and Hainmueller (Reference Eggers and Hainmueller2009) with multiple estimation methods.

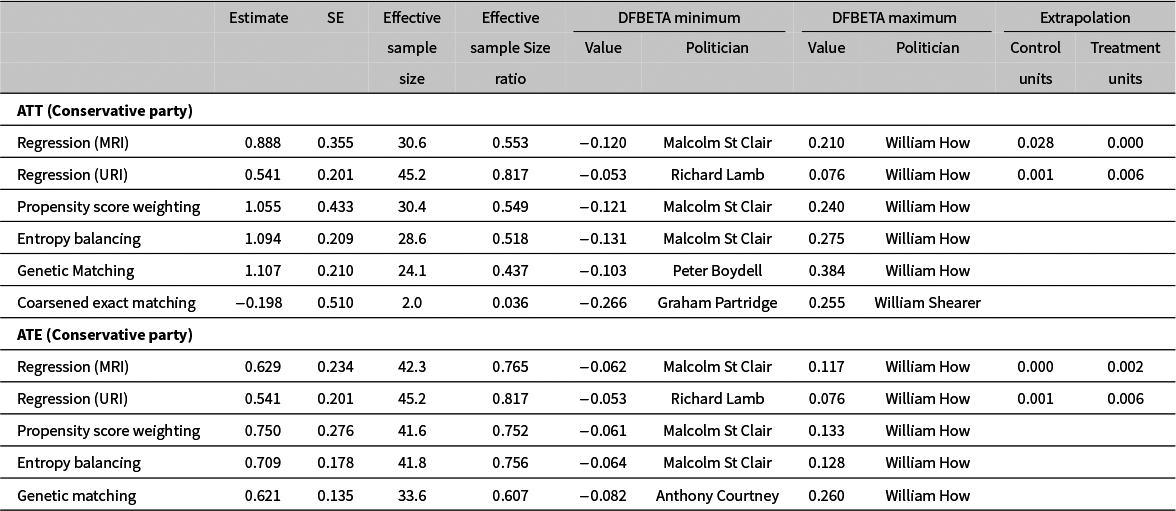
Note: The Regression (MRI) rows correspond to the MRI estimator of either ATT or ATE. The Regression (URI) rows correspond to the URI estimator which is an estimate of both ATT and ATE under the constant effects assumption. The Propensity Score Weighting rows correspond to the propensity score weighting estimator of either ATT or ATE in which the propensity scores are estimated via logistic regression. The Entropy Balancing rows correspond to the entropy balancing estimator of either ATT or ATE as implemented in the WeightIt R package. The Genetic Matching rows correspond to 1:1 matching on all X variables using the GenMatch function in the Matching R package. The Coarsened Exact Matching row corresponds to the coarsened exact matching estimator of ATT as implemented in the CEM R package. Note that the genetic matching results are slightly different from what is reported in Eggers and Hainmueller (Reference Eggers and Hainmueller2009). This appears to be due to the stochastic nature of the matching procedure. These slight differences do not affect the conclusions reached in Eggers and Hainmueller (Reference Eggers and Hainmueller2009).

As judged by our diagnostics, propensity score weighting and entropy balancing exhibit no serious problems. They have relatively large effective sample sizes, only moderately influential observations, and (by construction) they do not extrapolate.

Genetic matching results in a slightly lower effective sample size than the methods above and, when estimating ATT among Conservative Party members, it gives a good deal of influence to one observation (William How). Dropping just this one politician reduces the genetic matching ATT estimate from 1.107 to 0.723 and the ATE estimate drops from 0.621 to 0.361. Put another way, William How is responsible for roughly 38% of the estimated effect size.

In contrast to the other approaches, use of CEM with default settings results in an effective sample size of just two politicians which corresponds to an effective sample size ratio of just 0.036. In other words, CEM is discarding approximately 96% of the available data. This alone suggests that this application of CEM to this dataset should be questioned.

Figure 3 presents diagnostic plots for covariateFootnote ³⁸ balance in ATT estimation for Conservative MPs.Footnote ³⁹ The TASMD results in Figure 3a suggests that MRI, propensity score, entropy balancing, and genetic matching achieve mean balance for most covariates below the threshold. In contrast, CEM and, to a lesser extent, URI weighted data fail to balance many covariates and sometimes perform worse than the unweighted data. The KS statistics results in Figure 3b show that almost all methods contribute to reducing distributional imbalance. The test statistics also have less dispersion, partly because many covariates are binary variables.

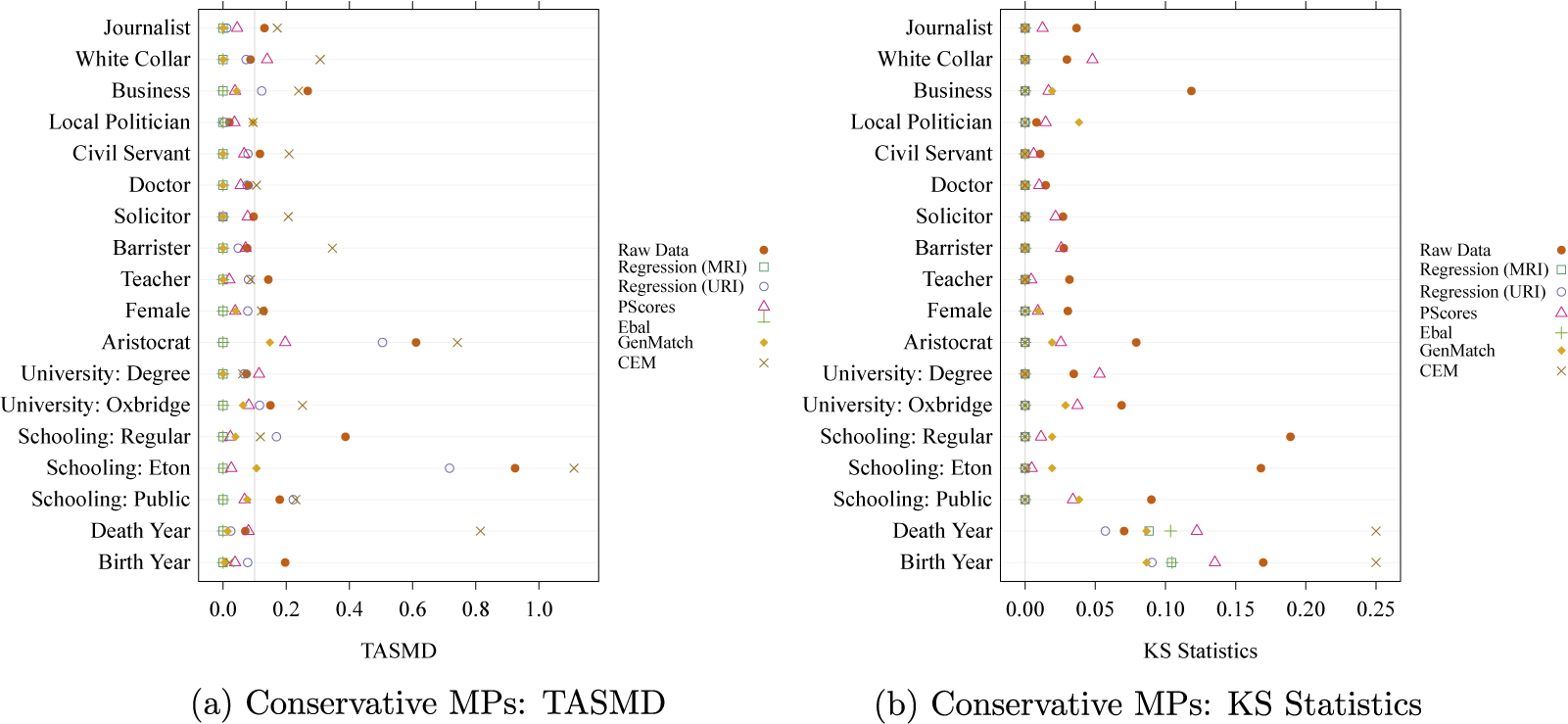
Figure 3 Weighted mean covariate balance (assessed by TASMD) and KS test statistics for control units using multiple ATT estimation methods in the re-analysis of Eggers and Hainmueller (Reference Eggers and Hainmueller2009).

Note: In the TASMD plot, each symbol represents the standardized difference between the weighted mean of the control data and the mean of the target data (i.e., the sample mean of that covariate among all treated units in the sample). The gray vertical line marks where the TASMD value is 0.1. In KS statistic plot, each symbol shows the maximum absolute difference in the ECDFs of the control and treated groups, using both raw and weighted control data. The gray vertical line marks KS statistics at 0.

Figure 3 suggests that genetic matching, the preferred method in the original paper, produces the best covariate balance without extrapolation. Examining weighted QQ-plots provides additional information on covariate balance. Again, for reasons of space, we limit attention to how genetic matching adjusts the distribution for the two continuous variables, Birth Year and Death Year among Conservative politicians. Figure 4 compares the distributional balance for these two covariates between control units and treated units. For both the Birth year and Death Year, the raw data already display good distributional balance. Genetic matching weights brings control units even closer to the target distribution, further improving balance on these covariates.

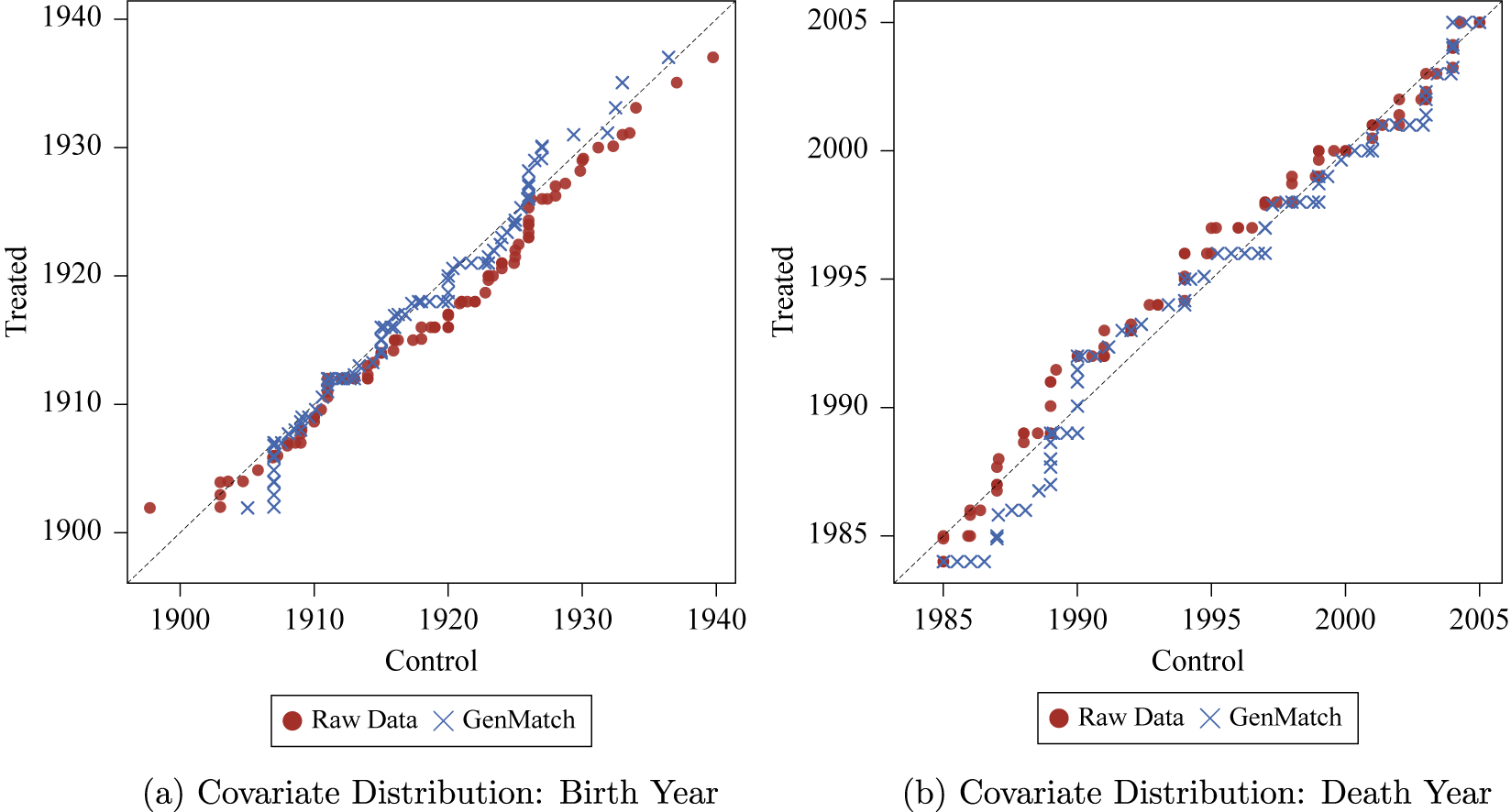
Figure 4 Quantile-quantile plot for Birth Year and Death Year with raw data and genetic matching weighted data for ATT estimation among conservative politicians.

Note: The X-axes show the weighted birth and death year quantiles for the control units, while the Y-axes shows the corresponding quantiles for the treated group, which is the target distribution in this case. Points on the 45-degree line correspond to equality of the quantiles represented by that point.

While there are reasons to think that that the propensity score weighting and entropy balancing results might be the most credible, the particular choice of estimation method matters relatively little as all approaches (with the exception of CEM) produce results that are qualitatively similar and in line with the authors’ hypothesis.