Two solutions to the problem of hierarchical data, with variables and processes at both higher and lower levels, vie for prominence in the social sciences. Fixed effects (FE) modeling is used more frequently in economics and political science, reflecting its status as the “gold standard” default (Schurer and Yong Reference Schurer and Yong2012, 1). However, random effects (RE) models—also called multilevel models, hierarchical linear models and mixed models—have gained increasing prominence in political science (Beck and Katz Reference Beck and Katz2007) and are used regularly in education (O'Connell and McCoach Reference O'Connell and McCoach2008), epidemiology (Duncan, Jones and Moon Reference Duncan, Jones and Moon1998), geography (Jones Reference Jones1991) and biomedical sciences (Verbeke and Molenberghs Reference Verbeke and Molenberghs2000, Reference Verbeke and Molenberghs2005). Both methods are applicable to research questions with complex structure, including place-based hierarchies (such as individuals nested within neighborhoods, for example Jones, Johnston and Pattie Reference Jones, Johnston and Pattie1992), and temporal hierarchies (such as panel data and time-series cross-sectional (TSCS) data,Footnote 1 in which measurement occasions are nested within entities such as individuals or countries (see Beck Reference Beck2007)). While this article is particularly concerned with the latter, its arguments apply equally to all forms of hierarchical data.Footnote 2
One problem with the disciplinary divides outlined above is that much of the debate between the two methods has remained separated by subject boundaries; the two sides of the debate often seem to talk past each other. This is a problem, because we believe that both sides are making important points that are currently not taken seriously by their counterparts. Since this article draws on a wide, multidisciplinary literature, we hope it will help inform each side of the relative merits of both sides of the argument.
Yet we take the strong, and rather heterodox, view that there are few, if any, occasions in which FE modeling is preferable to RE modeling. If the assumptions made by RE models are correct, RE would be the preferred choice because of its greater flexibility and generalizability, and its ability to model context, including variables that are only measured at the higher level. We show in this article that the assumptions made by RE models, including the exogeneity of covariates and the Normality of residuals, are at least as reasonable as those made by FE models when the model is correctly specified. Unfortunately, this correct formulation is used all too rarely (Fairbrother Reference Fairbrother2013), despite being fairly well known (it is discussed in numerous econometrics textbooks (Greene Reference Greene2012; Wooldridge Reference Wooldridge2002), if rather too briefly). Furthermore, we argue that, in controlling out context, FE models effectively cut out much of what is going on—goings-on that are usually of interest to the researcher, the reader and the policy maker. We contend that models that control out, rather than explicitly model, context and heterogeneity offer overly simplistic and impoverished results that can lead to misleading interpretations.
This article's title has two meanings. First, we hope to explain the technique of FE estimation to those who use it too readily as a default option without fully understanding what they are estimating and what they are losing by doing so. Second, we show that while the fixed dummy coefficients in the FE model are measured unreliably, RE models can explain (and thus reveal) specific differences between higher-level entities.
This article has three distinctive contributions. First, it is a central attack on the dominant method (FE) in much of the quantitative social sciences. Second, it advocates an alternative approach to endogeneity, in which its causes (separate ‘within’ and ‘between’ effects) are modeled explicitly. Third, it emphasizes the importance of modeling heterogeneity (not just overall mean effects) using random coefficients and cross-level interactions.
It is important to reiterate that our recommendations are not entirely one-sided: our proposed formulation is currently not used enough,Footnote 3 and in many disciplines endogeneity is often ignored. Furthermore, we want to be clear that the model is no panacea; there will remain biases in the estimates of higher-level effects if potential omitted variables are not identified, which needs to be considered carefully when the model is interpreted. However, our central point remains: a well-specified RE model can be used to achieve everything that FE models achieve, and much more besides.
The Problem of Hierarchies In Data, And The Re Solution
Many research problems in the social sciences have a hierarchical structure; indeed, “once you know hierarchies exist, you see them everywhere” (Kreft and De Leeuw Reference Kreft and De Leeuw1998, 1). Such hierarchies are produced because the population is hierarchically structured—voters at Level 1 are nested in constituencies at Level 2—and/or a hierarchical structure is imposed during data collection so that, for example in a longitudinal panel, there are repeated measures at Level 1 nested in individuals at Level 2. In the discussion that follows, and to make things concrete, we use ‘higher-level entities’ to refer to Level 2, and occasions to refer to Level 1. Consequently, time-varying observations are measured at Level 1 and time-invariant observations at Level 2; the latter are unchanging attributes. Thus in a panel study, higher-level entities are individuals, and time-invariant variables may include characteristics such as gender. In a TSCS analysis, the higher-level entities may be countries, and time-invariant variables could be whether they are located in the global south.Footnote 4
The technical problems of analyzing hierarchies in data are well known. Put briefly, standard ‘pooled’ linear regression models assume that residuals are independently and identically distributed. That is, once all covariates are considered, there are no further correlations (that is, dependence) between measures. Substantively, this means that the model assumes that any two higher-level entities are identical, and thus can be completely ‘pooled’ into a single population. With hierarchical data, particularly with temporal hierarchies that are often characterized by marked dependence over time, this is a patently unreasonable assumption. Responses for measurement occasions within a given higher-level entity are often related to each other. As a result, the effective sample size of such datasets is much smaller than a simple regression would assume: closer to the number of higher-level entities (individuals or countries) than the number of lower-level units (measurement occasions). As such, standard errors will be incorrectFootnote 5 if this dependence is not taken into account (Moulton Reference Moulton1986).
The RE solution to this dependency is to partition the unexplained residual variance into two: higher-level variance between higher-level entities and lower-level variance within these entities, between occasions. This is achieved by having a residual term at each level; the higher-level residual is the so-called random effect. As such, a simple standard RE model would be:
where
These are the ‘micro’ and ‘macro’ parts of the model, respectively, and they are estimated together in a combined model that is formed by substituting the latter into the former:
where yij is the dependent variable. In the ‘fixed’ part of the model, β 0 is the intercept term, x 1ij is a (series of) covariate(s) that are measured at the lower (occasion) level with coefficient β 1, and zj is a (series of) covariate(s) measured at the higher level with coefficient β 2. The ‘random’ part of the model (in brackets) consists of uj, the higher-level residual for higher-level entity j, allowing for differential intercepts for higher-level entities, and eij, the occasion-level residual for occasion i of higher-level entity j. The uj term is in effect a measure of ‘similarity’ that allows for dependence, as it applies to all the repeated measures of a higher-level entity. The variation that occurs at the higher level (including uj and any time-invariant variables) is considered in terms of the (smaller) higher-level entity sample size, meaning that the standard errors are correct. By assuming that uj and eij are Normally distributed, an overall measure of their respective variances can be estimated:
As such, we can say that we are ‘partially pooling’ our data by assuming that our higher-level entities, though not identical, come from a single distribution ![]() $$$\sigma _{u}^{2} $$$
—which is estimated from the data, much like the occasion-level variance
$$$\sigma _{u}^{2} $$$
—which is estimated from the data, much like the occasion-level variance ![]() $$$\sigma _{e}^{2} $$$
—and can itself be interpreted substantively.
$$$\sigma _{e}^{2} $$$
—and can itself be interpreted substantively.
These models must not only be specified, but also estimated on the basis of assumptions. Beck and Katz (Reference Beck and Katz2007) show that, with respect to TSCS data, RE models perform well, even when the Normality assumptions are violated.Footnote 6 Therefore they are preferred to both ‘complete pooling’ methods, which assume no differences between higher-level entities and FE, which do not allow for the estimation of higher-level, time-invariant parameters or residuals (see below). Shor et al. (Reference Shor, Bafumi, Keele and Park2007) use similar methods, but estimated using Bayesian Markov Chain Monte Carlo (MCMC) (rather than maximum likelihood) estimation, which they find produces estimates that are as good, or better than,Footnote 7 maximum likelihood RE and other methods.
The Problem of Omitted Variable Bias and Endogeneity in Re Models
Considering this evidence, one must consider why RE is not employed more widely, and remains rarely used in disciplines such as economics and political science. The answer lies in the exogeneity assumption of RE models: that the residuals are independent of the covariates; in particular, the assumptions concerning the occasion-level covariates and the two variance terms, such that:
In most practical applications, this is synonymous with:
The fact is that the above assumptionsFootnote 8 often do not hold in many standard RE models as formulated in Equation 1. Unfortunately, little attention has been paid to the substantive reasons why not. Indeed, the discovery of such endogeneity has regularly led to the abandonment of RE in favor of FE estimation, which models out higher-level variance and makes any correlations between that higher-level variance and covariates irrelevant, without considering the source of the endogeneity. This is unfortunate, because the source of the endogeneity is often itself interesting and worthy of modeling explicitly.
This endogeneity most commonly arises as a result of multiple processes related to a given time-varying covariate.Footnote 9 In reality, such covariates contain two parts: one that is specific to the higher-level entity that does not vary between occasions, and one that represents the difference between occasions, within higher-level entities:
These two parts of the variable can have their own different effects: called ‘between’ and ‘within’ effects, respectively, which together comprise the total effect of a given Level 1, time-varying variable. This division is inherent to the hierarchical structure present in both FE and RE models.
In Equation 1 above, it is assumed that the within and between effects are equal (Bartels Reference Bartels2008). That is, a one-unit change in xij for a given higher-level entity has the same statistical effect (β 1) as being a higher-level entity with an inherent time-invariant value of xij that is 1 unit greater. While this might well be the case, there are clearly many examples in which this is unlikely. Considering an example of TSCS country data, an increase in equality may have a different effect to generally being an historically more equal country, for example due to some historical attribute(s) (such as colonialism) of that country. Indeed, as Snijders and Bosker (Reference Snijders and Bosker2012, 60) argue, “it is the rule rather than the exception that within-group regression coefficients differ from between-group coefficients.”
Where the within and between effects are different, β 1 in Equation 1 will be an uninterpretable weighted average of the two processes (Krishnakumar Reference Krishnakumar2006; Neuhaus and Kalbfleisch Reference Neuhaus and Kalbfleisch1998; Raudenbush and Bryk Reference Raudenbush and Bryk2002, 137), while variance estimates are also affected (Grilli and Rampichini Reference Grilli and Rampichini2011). This can be thought of as omitted variable bias (Bafumi and Gelman Reference Bafumi and Gelman2006; Palta and Seplaki Reference Palta and Seplaki2003); because the between effect is omitted, β 1 attempts to account for both the within and the between effect of the covariate on the response, and if the two effects are different, it will fail to account fully for either. The variance that is left unaccounted for will be absorbed into the error terms u 0j and e 0ij, which will consequently both be correlated with the covariate, violating the assumptions of the RE model. When viewed in these terms, it is clear that this is a substantive inadequacy in the theory behind the RE model, rather than simply a statistical misspecification (Spanos Reference Spanos2006) requiring a technical fix.
The word ‘endogenous’ has multiple forms, causes and meanings. It can be used to refer to bias caused by omitted variables, simultaneity, sample selection or measurement error (Kennedy Reference Kennedy2008, 139). These are all different problems that should be dealt with in different ways. Therefore we consider the term to be misleading and, having explained it, do not use it in the rest of the article. The form of the problem that this article deals with is described rather more clearly by Li (Reference Li2011) as ‘heterogeneity bias,’ and we use that terminology from now on. Our focus on this does not deny the existence of other forms of bias that cause and/or result from correlated covariates and residuals.Footnote 10
FE Estimation
The rationale behind FE estimation is simple and persuasive, which explains why it is so regularly used in many disciplines. To avoid the problem of heterogeneity bias, all higher-level variance, and with it any between effects, are controlled out using the higher-level entities themselves (Allison Reference Allison2009), included in the model as dummy variables Dj:
To avoid having to estimate a parameter for each higher-level unit, the mean for higher-level entity is taken away from both sides of Equation 5, such that:
Because FE models only estimate within effects, they cannot suffer from heterogeneity bias. However, this comes at the cost of being unable to estimate the effects of higher-level processes, so RE is often preferred where the bias does not exist. In order to test for the existence of this form of bias in the standard RE model as specified in Equation 1, the Hausman specification test (Hausman Reference Hausman1978) is often used. This takes the form of comparing the parameter estimates of the FE and RE models (Greene Reference Greene2012; Wooldridge Reference Wooldridge2002) via a Wald test of the difference between the vector of coefficient estimates of each.
The Hausman test is regularly used to test whether RE can be used, or whether FE estimation should be used instead (for example Greene Reference Greene2012, 421). However, it is problematic when the test is viewed in terms of fixed and random effects, and not in terms of what is actually going on in the data. A negative result in a Hausman test tells us only that the between effect is not significantly biasing an estimate of the within effect in Equation 1. It “is simply a diagnostic of one particular assumption behind the estimation procedure usually associated with the random effects model… it does not address the decision framework for a wider class of problems” (Fielding Reference Fielding2004, 6). As we show later, the RE model that we propose in this article solves the problem of heterogeneity bias described above, and so makes the Hausman test, as a test of FE against RE, redundant. It is “neither necessary nor sufficient” (Clark and Linzer Reference Clark and Linzer2012, 2) to use the Hausman test as the sole basis of a researcher's ultimate methodological decision.
Problems with FE Models
Clearly, there are advantages to the FE model of Equations 5-6 over the RE models in Equation 1. By clearing out any higher-level processes, the model deals only with occasion-level processes. In the context of longitudinal data, this means considering differences over time, controlling out higher-level differences and processes absolutely, and supposedly “getting rid of proper nouns” (King Reference King2001, 504)—that is, distinctive, specific characteristics of higher-level units. This is why it has become the “gold standard” method (Schurer and Yong Reference Schurer and Yong2012, 1) in many disciplines. There is no need to worry about heterogeneity bias, and β 1 can be thought to represent the ‘causal effect.’
However, by removing the higher-level variance, FE models lose a large amount of important information. No inferences can be made about that higher-level variance, including whether or not it is significant (Schurer and Yong Reference Schurer and Yong2012, 14). Thus it is impossible to measure the effects of time-invariant variables at all, because all degrees of freedom at the higher level have been consumed. Where time-invariant variables are of particular interest, this is obviously critical. And yet even in these situations, researchers have suggested the use of FE, on the basis of a Hausman test. For example, Greene's (2012, 420) textbook gives an example of a study of the effect of schooling on future wages:
The value of the [Hausman] test statistic is 2,636.08. The critical value from the chi-squared table is 16.919 so the null hypothesis of a random effects model is rejected. We conclude that the fixed effects model is the preferred specification for these data. This is an unfortunate turn of events, as the main object of the study is the impact of education, which is a time invariant variable in this sample.
Unfortunate indeed! To us, explicating a method that fails to answer your research question is nonsensical. Furthermore, because the higher-level variance has been controlled out, any parameter estimates for time-varying variables deal with only a small subsection of the variance in that variable. Only within effects can be estimated (that is, the lower-level relationship net of any higher-level attributes), and so nothing can be said about a variable's between effects or a general effect (if one exists); studies that make statements about such effects on the basis of FE models are over-interpreting their results.
Beck and Katz (Beck Reference Beck2001; Beck and Katz Reference Beck and Katz2001) consider the example of the effect of a rarely changing variable, democracy, on a binary variable representing whether a pair of countries is at peace or at war (Green, Kim and Yoon Reference Green, Kim and Yoon2001; see also King Reference King2001; Oneal and Russett Reference Oneal and Russett2001). They show that estimates obtained under FE fail to show any relation between democracy and peace because it filters out all the effects of unchanging, time-invariant peace, which has an effect on time-variant democracy. In other words, time-invariant processes can have effects on time-varying variables, which are lost in the FE model. Countries that do not change their political regime, or do not change their state of peace (that is, most countries) are effectively removed from the sample. While this problem particularly applies to rarely changing, almost time-invariant variables (Plümper and Troeger Reference Plümper and Troeger2007), any time-varying covariate can have such time-invariant ‘between’ effects, which can be different from time-varying effects of the same variable, and these processes cannot be assessed in an FE model. Only an RE model can allow these processes to be modeled simultaneously.
Plümper And Troeger's FE Vector Decomposition
A method proposed by Plümper and Troeger (Reference Plümper and Troeger2007) allows time-invariant variables to be modeled within the framework of the FE model. They use an FE model before ‘decomposing’ the vector of fixed-effects dummies into that explained by a given time-invariant (or rarely changing) variable, and that which is not. They begin by estimating a standard dummy variable FE model as in Equation 5:
Here, Dj is a series of higher-level entity dummy variables, each with an associated intercept coefficient β 0j. Plümper and Troeger then regress in a separate higher-level model the vector of these estimated FE coefficients on time-invariant variables, such that
where zj is a (series of) higher-level variable(s) and Rj is the residual. This equation can be rearranged so that, once estimated, the values of Rj can be estimated as
Finally, Equation 8 is substituted into Equation 7 such that
where β 3 will equal exactly one (Greene Reference Greene2012, 405). The residual higher-level variance not explained by the higher-level variable(s) is modeled as a fixed effect, leaving no higher-level variance unaccounted for. As such, the model is very similar to an RE model (Equation 1), which does a similar thing but in a single overall model.Footnote 11 Stage 1 (Equation 7) is equivalent to the RE micro model, Stage 2 (Equation 8) to the macro model and Stage 3 (Equation 10) to the combined model. Just as with RE, the higher-level residual is assumed to be Normal (from the regression in Equation 8). What it does do differently is also control out any between effect of x 1ij in the estimation of β 1, meaning that these estimates will only include the within effect, as in standard FE models.
The FE vector decomposition (FEVD) estimator has been criticized by many in econometrics, who argue that the standard errors are likely to be incorrectly estimated (Breusch et al. Reference Breusch, Ward, Nguyen and Kompas2011a, Reference Breusch, Ward, Nguyen and Kompas2011b; Greene Reference Greene2011a, Reference Greene2011b, Reference Greene2012). Plümper and Troeger (Reference Plümper and Troeger2011) provide a method for calculating more appropriate standard errors, and so the FEVD model does work (at least with balanced data) when this method is utilized. However, our concern is that it retains many of the other flaws of FE models, which we have outlined above. It remains much less generalizable than an RE model—it cannot be extended to three (or more) levels, nor can coefficients be allowed to vary (as in a random coefficients model). It does not provide a nice measure of variance at the higher level, which is often interesting in its own right. Finally, it is heavily parameterized, with a dummy variable for each higher-level entity in the first stage, and thus can be relatively slow to run when there is a large number of higher-level units.
Plümper and Troeger also attempt to estimate the effects of ‘rarely changing’ variables, and their desire to do so using FE modeling suggests that they do not fully appreciate the difference between within and between effects. While they do not quantify what ‘rarely changing’ means, their motivation is to get significant results where FE produces insignificant results. FE models only estimate within effects, and so an insignificant effect of a rarely changing variable should be taken as saying that there is no evidence for a within effect of that variable. When Plümper and Troeger use FEVD to estimate the effects of rarely changing variables, they are in fact estimating between effects. Using FEVD to estimate the effects of rarely changing variables is not a technical fix for the high variance of within effects in FE models—it is shifting the goalposts and measuring something different. Furthermore, if between effects of rarely changing variables are of interest, then there is no reason why the between effects of other time-varying variables would not be, and so these should potentially be modeled as time-invariant variables as well.
An Re Solution to Heterogeneity Bias
What is needed is a solution, within the parsimonious, flexible RE framework, which allows for heterogeneity bias not to simply be corrected, but for it to be explicitly modeled. As it turns out, the solution is well documented, starting from an article by Mundlak (Reference Mundlak1978a). By understanding that heterogeneity bias is the result of attempting to model two processes in one term (rather than simply a cause of bias to be corrected), Mundlak's formulation simply adds one additional term in the model for each time-varying covariate that accounts for the between effect: that is, the higher-level mean. This is treated in the same way as any higher-level variable. Therefore in the simple case, the micro and macro models, respectively, are:
and
This combines to form
where xij is a (series of) time-variant variables, while ![]() $$${{\bar{x}}_j}$$$
is the higher-level entity j's mean; as such, the time-invariant component of those variables (Snijders and Bosker Reference Snijders and Bosker2012, 56). Here β 1 is an estimate of the within effect (as the between effect is controlled by
$$${{\bar{x}}_j}$$$
is the higher-level entity j's mean; as such, the time-invariant component of those variables (Snijders and Bosker Reference Snijders and Bosker2012, 56). Here β 1 is an estimate of the within effect (as the between effect is controlled by ![]() $$${{\bar{x}}_j}$$$
); β 3 is the ‘contextual’ effect that explicitly models the difference between the within and between effects. Alternatively, this can be rearranged by writing β 3 explicitly as this difference (Berlin et al., Reference Berlin, Kimmel, Ten Have and Sammel1999):
$$${{\bar{x}}_j}$$$
); β 3 is the ‘contextual’ effect that explicitly models the difference between the within and between effects. Alternatively, this can be rearranged by writing β 3 explicitly as this difference (Berlin et al., Reference Berlin, Kimmel, Ten Have and Sammel1999):
This rearranges to:
Now β 1 is the within effect and β 4 is the between effect of xij (Bartels Reference Bartels2008; Leyland Reference Leyland2010). This ‘within-between’ formulation (see Table 1) has three main advantages over Mundlak's original formulation. First, with temporal data it is more interpretable, as the within and between effects are clearly separated (Snijders and Bosker Reference Snijders and Bosker2012, 58). Second, in the first formulation, there is correlation between xij and ![]() $$${{\bar{x}}_j}$$$
; by group mean centering xij, this collinearity is lost, leading to more stable, precise estimates (Raudenbush Reference Raudenbush1989). Finally, if multicollinearity exists between multiple
$$${{\bar{x}}_j}$$$
; by group mean centering xij, this collinearity is lost, leading to more stable, precise estimates (Raudenbush Reference Raudenbush1989). Finally, if multicollinearity exists between multiple ![]() $$${{\bar{x}}_j}$$$
s and other time-invariant variables,
$$${{\bar{x}}_j}$$$
s and other time-invariant variables, ![]() $$${{\bar{x}}_j}$$$
s can be removed without the risk of heterogeneity bias returning to the occasion-level variables (as in the within model in Table 1).Footnote 12
$$${{\bar{x}}_j}$$$
s can be removed without the risk of heterogeneity bias returning to the occasion-level variables (as in the within model in Table 1).Footnote 12
Table 1 RE Model Formulations Considered

Note: the within-between and within-RE model involve group mean centering of the covariate. This is different from centering on the grand mean, which has a different purpose: to keep the value of the intercept (β 0) within the range of the data and to aid convergence of the model. Indeed, x 1ij and ![]() $$${{\bar{x}}_j}$$$
can be grand mean centered if required (the group mean-centered variables will already be centered on their grand mean by definition).
$$${{\bar{x}}_j}$$$
can be grand mean centered if required (the group mean-centered variables will already be centered on their grand mean by definition).
Just as before, the residuals at both levels are assumed to be Normally distributed:
As can be seen, this approach is algebraically similar to the FEVD estimator (Equation 10)—the mean term(s) are themselves interpretable time-invariant variablesFootnote 13 (Begg and Parides Reference Begg and Parides2003), measuring the propensity of a higher-level entity to be xij (in the binary case) or the average level of xij (in the continuous case) across the sample time period.Footnote 14 There are a few differences. First, estimates for the effects of time-invariant variables are controlled for by the means of the time-varying variables. While this could be done in Stage 2 of FEVD, it rarely is; nor is it suggested by Plümper and Troeger (Reference Plümper and Troeger2007) except for in the case of ‘rarely changing’ variables. Second, correct standard errors are automatically calculated, accounting for “multiple sources of clustering” (Raudenbush Reference Raudenbush2009, 473). Crucially, there can be no correlation between the group mean centered covariate and the higher-level variance, because each group mean centered covariate has a mean of zero for each higher-level entity j. Equally, at the higher level, the mean term is no longer constrained by Level 1 effects, so it is free to account for all the higher-level variance associated with that variable. As such, the estimate of β 1 in Equations 11 and 12 above will be identical to that obtained by FE, as Mundlak (Reference Mundlak1978a, 70) stated clearly:
When the model is properly specified, the GLSE [that is RE] is identical to the ‘within’ [that is, the FE] estimator. Thus there is only one estimator. The whole literature which has been based on an imaginary difference between the two estimators … is based on an incorrect specification which ignores the correlation between the effects and the explanatory variables.
While it is still possible that there is correlation between the group mean centered xij and eij, and between ![]() $$${{\bar{x}}_j}$$$
(and other higher-level variables) and uj (Kravdal Reference Kravdal2011), this is no more likely than in FE models for the former and aggregate regression for the latter, because we have accounted for the key source of this correlation by specifying the model correctly (Bartels Reference Bartels2008).Footnote 15 After all, “all models are wrong; the practical question is how wrong do they have to be to not be useful” (Box and Draper Reference Box and Draper1987, 74). How useful the model is depends, as with any model, on how well the researcher has accounted for possible omitted variables, simultaneity or other potential model misspecifications.
$$${{\bar{x}}_j}$$$
(and other higher-level variables) and uj (Kravdal Reference Kravdal2011), this is no more likely than in FE models for the former and aggregate regression for the latter, because we have accounted for the key source of this correlation by specifying the model correctly (Bartels Reference Bartels2008).Footnote 15 After all, “all models are wrong; the practical question is how wrong do they have to be to not be useful” (Box and Draper Reference Box and Draper1987, 74). How useful the model is depends, as with any model, on how well the researcher has accounted for possible omitted variables, simultaneity or other potential model misspecifications.
We see the FE model as a constrained form of the RE model,Footnote 16 meaning that the latter can encompass the former but not vice versa. By using the RE configuration, we keep all the advantages associated with RE modeling.Footnote 17 First, the ‘problem’ of heterogeneity bias across levels is not simply solved; it is explicitly modeled. The effect of xij is separated into two associations, one at each level, which are interesting, interpretable and relevant to the researcher (Enders and Tofighi Reference Enders and Tofighi2007, 130). Second, by assuming Normality of the higher-level variance, the model need only estimate a single term for each level (the variance), which are themselves useful measures, allowing calculation of the variance partitioning coefficient (VPC),Footnote 18 for example. Further, higher-level residuals (conditional on the variables in the fixed part of the model) are precision weighted or shrunken by multiplying by the higher-level entity's reliability λj (see Snijders and Bosker Reference Snijders and Bosker2012, 62),Footnote 19 calculated as:
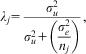 $${{\lambda }_j} = \frac{{\sigma _{u}^{2} }}{{\sigma _{u}^{2} + \left(\dfrac{{\sigma _{e}^{2} }}{{{{n}_j}}}\right)}},$$
$${{\lambda }_j} = \frac{{\sigma _{u}^{2} }}{{\sigma _{u}^{2} + \left(\dfrac{{\sigma _{e}^{2} }}{{{{n}_j}}}\right)}},$$
where nj is the sample size of higher-level entity j, ![]() $$$\sigma _{u}^{{\rm{2}}} $$$
is the between-entity variance and
$$$\sigma _{u}^{{\rm{2}}} $$$
is the between-entity variance and ![]() $$$\sigma _{e}^{{\rm{2}}} $$$
is the variance within higher-level entities, between occasions. One can thus estimate reliable residuals for each higher-level entity that are less prone to measurement error than FE dummy coefficients. By partially pooling by assuming that uj comes from a common distribution with a variance that has been estimated from the data, we can obtain much more reliable predictions for individual higher-level units (see Rubin Reference Rubin1980 for an early example of this).Footnote 20 While this is rarely of interest in individual panel data, it is likely to be of interest with TSCS data with repeated measures of countries.
$$$\sigma _{e}^{{\rm{2}}} $$$
is the variance within higher-level entities, between occasions. One can thus estimate reliable residuals for each higher-level entity that are less prone to measurement error than FE dummy coefficients. By partially pooling by assuming that uj comes from a common distribution with a variance that has been estimated from the data, we can obtain much more reliable predictions for individual higher-level units (see Rubin Reference Rubin1980 for an early example of this).Footnote 20 While this is rarely of interest in individual panel data, it is likely to be of interest with TSCS data with repeated measures of countries.
The methods we are proposing here are beginning to be taken up by researchers under the guise of a ‘hybrid’ or ‘compromise’ approach between FE and RE (Allison Reference Allison2009, 23; Bartels Reference Bartels2008; Greene Reference Greene2012, 421). Yet this is to misrepresent the nature of the model. There is nothing FE-like about the model at all—it is an RE model with additional time-invariant predictors. Perhaps as a consequence of this potentially misleading terminology, many of those who use such models fail to recognize its potential as an RE model. Allison (Reference Allison2009, 25), for example, argues that the effects of the mean variables (![]() $$${{\bar{x}}_j}$$$
) “are not particularly enlightening in themselves,” while many have suggested using the formulation as a form of the Hausman test and use the results to choose between fixed and random effects (Allison Reference Allison2009, 25; Baltagi Reference Baltagi2005; Greene Reference Greene2012, 421; Hsiao Reference Hsiao2003, 50; Wooldridge Reference Wooldridge2002, 290, Reference Wooldridge2009). Thus β 3 in Equation 11 is thought of simply as a measure of ‘correlation’ between xij and uj and when
$$${{\bar{x}}_j}$$$
) “are not particularly enlightening in themselves,” while many have suggested using the formulation as a form of the Hausman test and use the results to choose between fixed and random effects (Allison Reference Allison2009, 25; Baltagi Reference Baltagi2005; Greene Reference Greene2012, 421; Hsiao Reference Hsiao2003, 50; Wooldridge Reference Wooldridge2002, 290, Reference Wooldridge2009). Thus β 3 in Equation 11 is thought of simply as a measure of ‘correlation’ between xij and uj and when ![]() $$${{\beta }_3} \ne 0$$$
in Equation 11, or
$$${{\beta }_3} \ne 0$$$
in Equation 11, or ![]() $$${{\beta }_1} \ne {{\beta }_4}$$$
in Equation 12, the Hausman test fails and it is argued that the FE model should be used. It is clear to us (and to Skrondal and Rabe-Hesketh Reference Skrondal and Rabe-Hesketh2004, 53; Snijders and Berkhof Reference Snijders and Berkhof2007, 145), however, that the use of this model makes that choice utterly unnecessary.
$$${{\beta }_1} \ne {{\beta }_4}$$$
in Equation 12, the Hausman test fails and it is argued that the FE model should be used. It is clear to us (and to Skrondal and Rabe-Hesketh Reference Skrondal and Rabe-Hesketh2004, 53; Snijders and Berkhof Reference Snijders and Berkhof2007, 145), however, that the use of this model makes that choice utterly unnecessary.
To reiterate, the Hausman test is not a test of FE versus RE; it is a test of the similarity of within and between effects. An RE model that properly specifies the within and between effects will provide identical results to FE, regardless of the result of a Hausman test. Furthermore, between effects, other higher-level variables and higher-level residuals (none of which can be estimated with FE) should not be dismissed lightly; they are often enlightening, especially for meaningful entities such as countries. For these reasons, and the ease with which they can now be fitted in most statistical software packages, RE models are the obvious choice.
Simulations
We now present simulations results that show that, under a range of situations, the RE solution that we propose performs at least as well as the alternatives on offer—it predicts the same effects as both FE and FEVD for time-varying variables, and the same results as FEVD for time-invariant variables. Furthermore, the simulations show that standard errors are poorly estimated by FEVD when there is imbalance in the data.
The simulationsFootnote 21 are similar to those conducted by Plümper and Troeger (Reference Plümper and Troeger2007), using the following underlying data generating process:
where
β 0 = 1, β 1 = 0.5, β 2 = 2, β 3 = −1.5, β 4 = −2.5, β 5 = 1.8, β 6 = 3.
In order to simulate correlation between x 3ij and uj, the value of β 3C varies (-1, 0, 1, 2) between simulations. This parameter is also estimated in its own right—as we have argued, it is often of substantive interest in itself. We also vary the extent of correlation between z3j and uj (-0.2, 0, 0.2, 0.4, 0.6). All variables were generated to be Normally distributed with a mean of zero—fixed part variables with a standard deviation of 1, Level 1 and 2 residuals with standard deviations of 3 and 4, respectively. In addition, we varied the sample size—both the number of Level 2 units (100, 30) and the number of time points (20, 70). Additionally we tested the effect of imbalance in the data (no missingness, 50 percent missingness in all but five of the higher-level units) on the performance of the various estimators. The simulations were run in Stata using the xtreg and xtfevd commands.
For each simulation scenario, the data were generated and models estimated 1,000 times, and three quantities were calculated: bias, root mean square error (RMSE) and optimism, calculated as in Shor et al. (Reference Shor, Bafumi, Keele and Park2007) and in line with the simulations presented by Plümper and Troeger (Reference Plümper and Troeger2007, Reference Plümper and Troeger2011). Bias is the mean of the ratios of the true parameter value to the estimated parameter, and so a value of 1 suggests that the model estimates are, on average, exactly correct. RMSE also assesses bias, as well as efficiency: the lower the value, the more accurate and precise the estimator. Finally, optimism evaluates how the standard errors compare to the true sampling variability of the simulations; values greater than 1 suggest that the estimator is overconfident in its estimates, while values below 1 suggest that they are more conservative than necessary.
Table 2 presents the results from some permutations of the simulations when the data is balanced. As can be seen, and as expected, the standard RE estimator is outperformed by the other estimators, because of bias resulting from the omission of the between effect associated with X3 from the model. It can also be seen that the within-between RE model (REWB) performs at least as well as both FE and FEVD for all three measures. What is more surprising is the effect of data imbalance (see Table 3) on the performance of the estimators—while for RE, FE and REWB the results remain much the same, the standard errors are estimated poorly by the FEVD—too high (type 2 errors) for lower-level variables and too low (type 1 errors) for higher-level variables. The online appendices show that this result is repeated for all the simulation scenarios that we tested, regardless of the size of correlations present in the data and the data sample size. It is clear that it would be unwise to use the FEVD with unbalanced data, and even when data is balanced, Mundlak's (1978a) claim, that the models will produce identical results, is fully justified.
Table 2 RMSE, Bias and Optimism from the Simulation Results over Five Permutations (times 1,000 estimations)
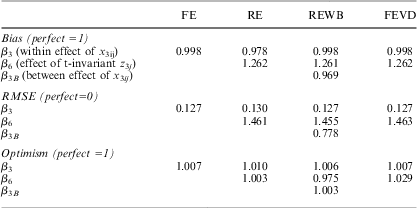
Note: units (30), time periods (20) and the contextual effect size (1) are kept constant. Correlation between Z3 and uj varies, with values -0.2, 0, 0.2, 0.4 and 0.6. The data are balanced.
Table 3 RMSE, Bias and Optimism from the Simulation Results over Five Permutations (times 1,000 estimations)

Note: units (30), time periods (20) and the contextual effect size (1) are kept constant. Correlation between Z3 and uj varies, with values -0.2, 0, 0.2, 0.4 and 0.6. The data are unbalanced.
Having shown that the REWB model produces results that are at least as unbiased as alternatives including FE and FEVD, the question remains why one should choose the RE option over these others. If higher-level variables and/or shrunken residuals are not of substantive interest, why not simply estimate an FE regression (or the FEVD estimator if time-invariant variables or other between effects happen to be of interest and the data is balanced)? The answer is twofold. First, with the ability to estimate both effects in a single model (rather than the three steps of the FEVD estimator), the RE model is more general than the other models. We believe it is valuable to be able to model things in a single coherent framework. Second, and more importantly, the RE model can be extended to allow for variation in effects across space and time to be explicitly modeled, as we show in the following section. That is, while FE models assume a priori that there is a single effect that affects all higher-level units in the same way, the RE framework allows for that assumption to be explicitly tested. This does not simply provide additional results to those already found—failing to do this can lead to results that are seriously and substantively misleading.
Extending The Basic Model: Random Coefficient Models And Cross-Level Interactions
We have argued that the main advantage of RE models is their generalizability and extendibility, and this section outlines oneFootnote 22 such extension: the random coefficient model (RCM). This allows the effects of β coefficients to vary by the higher-level entities (Bartels Reference Bartels2008; Mundlak Reference Mundlak1978b; Schurer and Yong Reference Schurer and Yong2012). Heteroscedasticity at the occasion level can also be explicitly modeled by including additional random effects at Level 1. Thus our model could become:
where
These equations (one micro and two macro) combine to form:
with the following distributional assumptions:
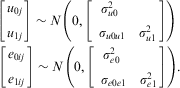 $$\matrix {\left[ {\matrix{ {{{u}_{{\rm{0}}j}}} \cr{{{u}_{{\rm{1}}j}}} \\\end{}} }\right] \sim N\left( {0,\left[ {\matrix {{\sigma _{{u{\rm{0}}}}^{{\rm{2}}} } & {} \cr\ {{{\sigma }_{u{\rm{0}}u{\rm{1}}}}} & {\sigma _{{u{\rm{1}}}}^{{\rm{2}}} } \\\end{}}} \right]} \right) \cr\ \left[ {\matrix{ {{{e}_{{\rm{0}}ij}}} \cr{{{e}_{{\rm{1}}ij}}} \\\end{}}} \right] \sim N\left( {0,\left[ {\matrix{ {\sigma _{{e{\rm{0}}}}^{{\rm{2}}} } & {} \cr\ {{{\sigma }_{e{\rm{0}}e{\rm{1}}}}} & {\sigma _{{e{\rm{1}}}}^{{\rm{2}}} }} \\\end{}} \right]} \right). \\ \end{}$$
$$\matrix {\left[ {\matrix{ {{{u}_{{\rm{0}}j}}} \cr{{{u}_{{\rm{1}}j}}} \\\end{}} }\right] \sim N\left( {0,\left[ {\matrix {{\sigma _{{u{\rm{0}}}}^{{\rm{2}}} } & {} \cr\ {{{\sigma }_{u{\rm{0}}u{\rm{1}}}}} & {\sigma _{{u{\rm{1}}}}^{{\rm{2}}} } \\\end{}}} \right]} \right) \cr\ \left[ {\matrix{ {{{e}_{{\rm{0}}ij}}} \cr{{{e}_{{\rm{1}}ij}}} \\\end{}}} \right] \sim N\left( {0,\left[ {\matrix{ {\sigma _{{e{\rm{0}}}}^{{\rm{2}}} } & {} \cr\ {{{\sigma }_{e{\rm{0}}e{\rm{1}}}}} & {\sigma _{{e{\rm{1}}}}^{{\rm{2}}} }} \\\end{}} \right]} \right). \\ \end{}$$
These variances and covariances can be used to form quadratic ‘variance functions’ (Goldstein Reference Goldstein2010, 73) to see how the variance varies with ![]() $$$\left( {{{x}_{ij}}\,{\rm{ - }}\,{{{\bar{x}}}_j}} \right)$$$
. At the higher level, the total variance is calculated by
$$$\left( {{{x}_{ij}}\,{\rm{ - }}\,{{{\bar{x}}}_j}} \right)$$$
. At the higher level, the total variance is calculated by
and at Level 1, it is
These can often be substantively interesting, as well as correct misspecification of a model that would otherwise assume homogeneity at each level (Rasbash et al. Reference Rasbash, Steele, Browne and Goldstein2009, 106). As such, even when time-invariant variables are not of interest, the RE model is preferable because it means that “a richer class of models can be estimated” (Raudenbush Reference Raudenbush2009, 481), and rigid assumptions of FE and FEVD can be relaxed.
RCMs additionally allow cross-level interactions between higher- and lower-level variables. In the TSCS case, that is an interaction between a variable measured at the country level and one measured at the occasion level. This is achieved by extending Equation 15 to, for example:
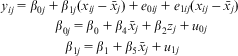 $$\matrix{ {{y}_{ij}}\, = \,{{\beta }_{{\rm{0}}j}}\, + \,{{\beta }_{{\rm{1}}j}}({{x}_{ij}}\,{\rm{ - }}\,{{{\bar{x}}}_j})\, + \,{{e}_{{\rm{0}}ij}}\, + \,{{e}_{{\rm{1}}ij}}({{x}_{ij}}\,{\rm{ - }}\,{{{\bar{x}}}_j}) \cr\ \ \ \ \ {{\beta }_{{\rm{0}}j}}\, = \,{{\beta }_{\rm{0}}}\, + \,{{\beta }_{\rm{4}}}{{{\bar{x}}}_j}\, + \,{{\beta }_{\rm{2}}}{{z}_j}\, + \,{{u}_{{\rm{0}}j}} \cr\ {{\beta }_{{\rm{1}}j}}\, = \,{{\beta }_{\rm{1}}}\, + \,{{\beta }_{\rm{5}}}{{{\bar{x}}}_j}\, + \,{{u}_{{\rm{1}}j}} \\ \end{}$$
$$\matrix{ {{y}_{ij}}\, = \,{{\beta }_{{\rm{0}}j}}\, + \,{{\beta }_{{\rm{1}}j}}({{x}_{ij}}\,{\rm{ - }}\,{{{\bar{x}}}_j})\, + \,{{e}_{{\rm{0}}ij}}\, + \,{{e}_{{\rm{1}}ij}}({{x}_{ij}}\,{\rm{ - }}\,{{{\bar{x}}}_j}) \cr\ \ \ \ \ {{\beta }_{{\rm{0}}j}}\, = \,{{\beta }_{\rm{0}}}\, + \,{{\beta }_{\rm{4}}}{{{\bar{x}}}_j}\, + \,{{\beta }_{\rm{2}}}{{z}_j}\, + \,{{u}_{{\rm{0}}j}} \cr\ {{\beta }_{{\rm{1}}j}}\, = \,{{\beta }_{\rm{1}}}\, + \,{{\beta }_{\rm{5}}}{{{\bar{x}}}_j}\, + \,{{u}_{{\rm{1}}j}} \\ \end{}$$
which combine to form:
The models can thus give an indication of whether the effect of a time-varying predictor varies by time-invariant predictors (or vice versa), and this is quantified by the coefficient β 5. Note that these could include interactions between the time-variant and time-invariant parts of the same variable, as is the case above, or could involve other time-invariant variables. The possibility of such interactions is not new (Davis, Spaeth and Huson Reference Davis, Spaeth and Huson1961); they have been an established part of the multilevel modeling literature for many years (Jones and Duncan Reference Jones and Duncan1995, 33). While the interaction terms themselves can be included in an FE model (for example see Boyce and Wood Reference Boyce and Wood2011; Wooldridge Reference Wooldridge2009), it is only when they are considered together with the additive effects of the higher-level variable (β 4) that their full meaning can be properly established. This can only be done in a random coefficient model. Such relationships ought to be of interest to any researcher studying time-varying variables. If the effect of a time-varying education policy is different for boys and girls, the researcher needs to know this. It is even conceivable that such relationships could be in opposite directions for different types of higher-level entities. Therefore, an FE study that suggests that a policy generally helps everyone could be hiding the fact that it actually hinders certain types of people. Resources could be wasted applying a policy to individuals who are harmed by it. Following Pawson (Reference Pawson2006), we believe that context should be central to any evidence-based policy.
To reiterate this point, even when time-invariant variables are not directly relevant to the research question itself, it is important to think about what is happening at the higher level, in a multilevel RE framework. Simpler models that control out context assume that occasion-level covariates have only ‘stylized’ (see Clark Reference Clark1998; Kaldor Reference Kaldor1961; Solow Reference Solow1988, 2) mean effects that affect all higher-level entities in exactly the same way. This leads to nice simple conclusions (a policy either works or does not), but it misses out important information about what is going on:
Continuing to do individual-level analyses stripped out of its context will never inform us about how context may or may not shape individual and ecological outcomes (Subramanian et al. Reference Subramanian, Jones, Kaddour and Krieger2009a, 355).
An example illustrating the ideas presented in this article can be found online,Footnote 23 where we reanalyze the data used by Milner and Kubota (Reference Milner and Kubota2005) in their FE study of democracy and free trade. A Hausman test would suggest that for this dataset, an FE model should be used; we show that doing so leads to considerably impoverished results.
Conclusions
In the introduction to his book on FE models, Allison (Reference Allison2009, 2) criticizes an early proponent of RE:
Such characterisations are very unhelpful in a nonexperimental setting, however, because they suggest that a random effects approach is nearly always preferable. Nothing could be further from the truth.
We have argued in this article that the RE approach is, in fact, nearly always preferable. We have shown that the main criticism of RE, the correlation between covariates and residuals, is readily solvable using the within-between formulation espoused here, although the solution is used all too rarely in RE modeling. This is why, in fact, Allison argues in favor of the same RE formulation that we have used, even though he calls it a ‘hybrid’ solution. Our strong position is not simply based on finding a technical fix, however. We believe that understanding the role of context (households, individuals, neighborhoods, countries, etc.) that defines the higher level, is usually of profound importance to a given research question—one must model it explicitly—and requires the use of an RE model that analyzes and separates both the within and between components of an effect explicitly, and assesses how those effects vary over time and space rather than assuming heterogeneity away with FE:
Heterogeneity is not a technical problem calling for an econometric solution but a reflection of the fact that we have not started on our proper business, which is trying to understand what is going on (Deaton Reference Deaton2010, 430).
This point is as much philosophical as it is statistical (Jones Reference Jones2010). We as researchers are aiming to understand the world. FE models attempt to do this by cutting out much of “what is going on,” leaving only a supposedly universal effect and controlling out differences at the higher level. In contrast, an RE approach explicitly models this difference, leading “to a richer description of the relationship under scrutiny” (Subramanian et al. Reference Subramanian, Jones, Kaddour and Krieger2009b, 373). To be absolutely clear, this is not to say that within-between RE models are perfect—no model is. If there are only a very small number of higher-level units, RE may not be appropriate. As with any model, it is important to consider whether important variables have been omitted and whether causal interpretations are justified, using theory—particularly regarding time-invariant variables. No statistical model can act as a substitute for intelligent research design and forethought regarding the substantive meaning of parameters. However, the advantages of within-between RE over the more restrictive FE are at odds with the dominance of FE as the ‘default’ option in a number of social science disciplines. We hope this article will go some way toward ending that dominance and stimulating much-needed debate on this issue.
Supplementary material
To view supplementary material for this article, please visit http://dx.doi.org/10.1017/psrm.2014.7

 The multilevel modeling literature has not significantly engaged with the Mundlak formulation or the issue of endogeneity.
The multilevel modeling literature has not significantly engaged with the Mundlak formulation or the issue of endogeneity.


