Hostname: page-component-76c49bb84f-c7tcl Total loading time: 0 Render date: 2025-07-09T23:33:42.746Z Has data issue: false hasContentIssue false
  • English
  • Français

A Frostman-Type Lemma for Sets with Large Intersections, and an Application to Diophantine Approximation

Part of: Diophantine approximation, transcendental number theory Classical measure theory Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  27 October 2014

Tomas Persson  and
Henry W. J. Reeve
Tomas Persson
Affiliation:
Centre for Mathematical Sciences, Lund University, Box 118, SE-22100 Lund, Sweden, (tomasp@maths.lth.se)
Henry W. J. Reeve
Affiliation:
Department of Mathematics, University of Bristol, University Walk, Clifton, Bristol BS8 1TW, UK, (henrywjreeve@gmail.com)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

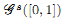We consider classes of subsets of [0, 1], originally introduced by Falconer, that are closed under countable intersections, and such that every set in the class has Hausdorff dimension at least s. We provide a Frostman-type lemma to determine if a limsup set is in such a class. Suppose that E = lim sup En ⊂ [0, 1], and that μn are probability measures with support in En. If there exists a constant C such that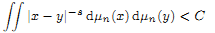

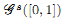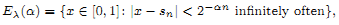
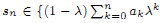for all n, then, under suitable conditions on the limit measure of the sequence (μn), we prove that the set E is in the class .

As an application we prove that, for α > 1 and almost all λ ∈ (½, 1), the set

where and ak ∈ {0, 1}}, belongs to the class 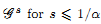. This improves one of our previously published results.

Keywords

diophantine approximationHausdorff dimensionclasses with large intersections

MSC classification

Primary: 11J83: Metric theory
Secondary: 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension 28A78: Hausdorff and packing measures 28A80: Fractals

Information

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 58 , Issue 2 , June 2015 , pp. 521 - 542
Copyright
Copyright © Edinburgh Mathematical Society 2014 

References

1.Bugeaud, Y., Intersective sets and Diophantine approximation, Michigan Math. J. 52 (2004), 667–682.CrossRefGoogle Scholar
2.Falconer, K., Classes of sets with large intersections, Mathematika 32(2) (1985), 191–205.CrossRefGoogle Scholar
3.Falconer, K., Sets with large intersection properties, J. Lond. Math. Soc. 49(2) (1994), 267–280.CrossRefGoogle Scholar
4.Palis, J. and Yoccoz, J.-C., Homoclinic tangencies for hyperbolic sets of large Hausdorff dimension, Acta Math. 172 (1994), 91–136.CrossRefGoogle Scholar
5.Persson, T. and Reeve, H., On the Diophantine properties of λ-expansions, Mathematika 59(1) (2013), 65–86.CrossRefGoogle Scholar
6.Solomyak, B., On the random series Σ±λn (an Erdös problem), Annals Math. 142(3) (1995), 611–625.CrossRefGoogle Scholar