No CrossRef data available.
Article contents
On the Range Inclusion for Normal Derivations on C*-algebras
Published online by Cambridge University Press: 22 February 2017
Abstract
For a von Neumann subalgebra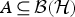 
$A \, \subseteq \, {\cal B}({\cal H})$ and any two elements a, b ∈ A with a normal, such that the corresponding derivations d a and d b satisfy the condition ‖d b (x)‖ ≤ ‖d a (x)‖ for all x ∈ A, there exist completely bounded (a)ʹ-bimodule map 
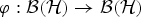$\varphi : {\cal B}({\cal H}) \rightarrow {\cal B}({\cal H})$ such that d b |A = φ d a |A=d a φ|A. (In particular d b (A) ⊆ d a (A).) Moreover, if A is a factor, then φ can be taken to be normal and these equalities hold on 
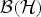${\cal B}({\cal H})$ instead of just on A. This result is not true for general (even primitive) C*-algebras 
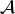${\cal A}$ .
Information
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 61 , Issue 1 , February 2018 , pp. 1 - 11
- Copyright
- Copyright © Edinburgh Mathematical Society 2018
References
1
Aleksandrov, A. B., Peller, V. V., Potapov, D. and Sukochev, F., Functions of normal operators under perturbations, Adv. Math.
226 (2011), 5216–5251.Google Scholar
2
Ara, P. and Mathieu, M., Local multipliers of C*-algebras, Springer Monographs in Mathematics (Springer, 2003).Google Scholar
3
Archbold, R. J., Kaniuth, E. and Somerset, D. W. B., Norms of inner derivations for multiplier algebras of C*-algebras and group C*-algebras II, Adv. Math.
280 (2015), 225–255.Google Scholar
4
Bonsall, F. F. and Duncan, J., Complete Normed Algebras, Ergebnisse der Mathematik und ihrer Grenzgebiete Volume 80 (Springer, 1973).Google Scholar
5
Brešar, M., The range and kernel inclusion of algebraic derivations and commuting maps, Q. J. Math.
56 (2005), 31–41.Google Scholar
6
Brešar, M., Magajna, B. and Špenko, S., Identifying derivations through the spectra of their values, Integ. Eqns Operat. Theory
73, (2012), 395–411.Google Scholar
7
Elliott, G. A. and Zsido, L., Almost uniformly continuous automorphism groups of operator algebras, J. Operat. Theory
8 (1982), 227–277.Google Scholar
8
Fong, C. K., Range inclusion for normal derivations, Glasgow Math. J.
25 (1984), 255–262.Google Scholar
9
Glimm, J., A Stone-Weierstrass theorem for C*-algebras, Ann. Math.
72 (1960), 216–244.Google Scholar
10
Halpern, H., Irreducible module homomorphisms of a von Neumann algebra into its center, Trans. Am. Math. Soc.
140 (1969), 195–221.Google Scholar
12
Johnson, B. E. and Williams, J.P., The range of a normal derivation, Pac. J. Math.
58 (1975), 105–122.Google Scholar
13
Kissin, E. and Shulman, V. S., On the range inclusion of normal derivations: variations on a theme by Johnson, Williams and Fong, Proc. Lond. Math. Soc.
83 (2001), 176–198.Google Scholar
14
Kissin, E. and Shulman, V. S., Classes of operator smooth functions, I, operator Lipschitz functions, Proc. Edinb. Math. Soc.
48 (2005), 151–173.Google Scholar
15
Magajna, B., The Haagerup norm on the tensor product of operator modules, J. Funct. Analysis
129 (1995), 325–348.Google Scholar
16
Magajna, B., Variance of operators and derivations, J. Math. Analysis Applic.
433 (2016), 1–30.Google Scholar
18
Paulsen, V. I., Completely bounded maps and operator algebras, Cambridge Studies in Advanced Mathematics, Volume 78 (Cambridge University Press, 2002).Google Scholar
20
Sinclair, A. M. and Roger Smith, R., Hochschild cohomology of von Neumann algebras, London Mathematical Society Lecture Notes Series, Volume 203 (Cambridge Universit Press, 1995).Google Scholar
21
Smith, R. R., Completely bounded module maps and the Haagerup tensor product, J. Funct. Analysis
102 (1991), 156–175.Google Scholar