Published online by Cambridge University Press: 22 June 2021
We compute the deficiency spaces of operators of the form $H_A{\hat {\otimes }} I + I{\hat {\otimes }} H_B$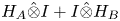 , for symmetric $H_A$
, for symmetric $H_A$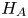 and self-adjoint $H_B$
and self-adjoint $H_B$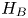 . This enables us to construct self-adjoint extensions (if they exist) by means of von Neumann's theory. The structure of the deficiency spaces for this case was asserted already in Ibort et al. [Boundary dynamics driven entanglement, J. Phys. A: Math. Theor.47(38) (2014) 385301], but only proven under the restriction of $H_B$
. This enables us to construct self-adjoint extensions (if they exist) by means of von Neumann's theory. The structure of the deficiency spaces for this case was asserted already in Ibort et al. [Boundary dynamics driven entanglement, J. Phys. A: Math. Theor.47(38) (2014) 385301], but only proven under the restriction of $H_B$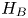 having discrete, non-degenerate spectrum.
having discrete, non-degenerate spectrum.
Address at the time of publication: IST Austria, Klosterneuburg, Austria.