Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-24T21:17:47.064Z Has data issue: false hasContentIssue false
  • English
  • Français

Structure theory and stable rank for C*-algebras of finite higher-rank graphs

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  04 October 2021

David Pask Open the ORCID record for David Pask [Opens in a new window] ,
Adam Sierakowski Open the ORCID record for Adam Sierakowski [Opens in a new window]  and
Aidan Sims Open the ORCID record for Aidan Sims [Opens in a new window]
David Pask
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, WollongongNSW2522, Australia(dpask@uow.edu.au; asierako@uow.edu.au; asims@uow.edu.au)
Adam Sierakowski
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, WollongongNSW2522, Australia(dpask@uow.edu.au; asierako@uow.edu.au; asims@uow.edu.au)
Aidan Sims
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, WollongongNSW2522, Australia(dpask@uow.edu.au; asierako@uow.edu.au; asims@uow.edu.au)
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the structure and compute the stable rank of $C^{*}$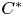-algebras of finite higher-rank graphs. We completely determine the stable rank of the $C^{*}$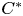-algebra when the $k$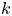-graph either contains no cycle with an entrance or is cofinal. We also determine exactly which finite, locally convex $k$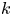-graphs yield unital stably finite $C^{*}$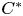-algebras. We give several examples to illustrate our results.

Keywords

higher-rank graphstable rankC*-algebraoperator algebra

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 4 , November 2021 , pp. 822 - 847
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

an Huef, A. and Raeburn, I., The ideal structure of Cuntz-Krieger algebras, Ergodic Theory Dynam. Syst. 17(3) (1997), 611–624.CrossRefGoogle Scholar
Blackadar, B., Operator algebras, Encyclopaedia of Mathematical Sciences, Volume 122 (Springer-Verlag, Berlin, 2006). Theory of $C^{*}$-algebras and von Neumann algebras, Operator Algebras and Non-commutative Geometry, III.CrossRefGoogle Scholar
Brown, L. G., On higher real and stable ranks for $CCR$ $C^{*}$-algebras, Trans. Amer. Math. Soc. 368(10) (2016), 7461–7475.CrossRefGoogle Scholar
Brown, J. H., Clark, L. O. and an Huef, A., Dense subalgebras of purely infinite simple groupoid C*-algebras, Proc. Edinb. Math. Soc. (2) 63(3) (2020), 609–629.CrossRefGoogle Scholar
Carlsen, T. M., Kang, S., Shotwell, J. and Sims, A., The primitive ideals of the Cuntz-Krieger algebra of a row-finite higher-rank graph with no sources, J. Funct. Anal. 266(4) (2014), 2570–2589.CrossRefGoogle Scholar
Castillejos, J., Evington, S., Tikuisis, A., White, S. and Winter, W., Nuclear dimension of simple $C^{\ast }$-algebras, Invent. Math. 224 (2021), 245–290.CrossRefGoogle Scholar
Clark, L. O., an Huef, A. and Sims, A., AF-embeddability of 2-graph algebras and quasidiagonality of $k$-graph algebras, J. Funct. Anal. 271(4) (2016), 958–991.10.1016/j.jfa.2016.04.024CrossRefGoogle Scholar
Dădărlat, M., Nagy, G., Némethi, A. and Pasnicu, C., Reduction of topological stable rank in inductive limits of $C^{*}$-algebras, Pacific J. Math. 153(2) (1992), 267–276.CrossRefGoogle Scholar
Davidson, K. R. and Yang, D., Representations of higher rank graph algebras, New York J. Math. 15 (2009), 169–198.Google Scholar
Deicke, K., Hong, J. H. and Szymański, W., Stable rank of graph algebras. Type I graph algebras and their limits, Indiana Univ. Math. J. 52(4) (2003), 963–979.CrossRefGoogle Scholar
Eilers, S. and Elliott, G. A., The Riesz property for the $K_*$-group of a $C^{*}$-algebra of minimal stable and real rank, C. R. Math. Acad. Sci. Soc. R. Can. 25(4) (2003), 108–113.Google Scholar
Elliott, G. A., Ho, T. M. and Toms, A. S., A class of simple $C^{*}$-algebras with stable rank one, J. Funct. Anal. 256(2) (2009), 307–322.CrossRefGoogle Scholar
Elliott, G. A. and Niu, Z., On the classification of simple amenable $C^{*}$-algebras with finite decomposition rank, in Operator algebras and their applications, pp. 117–125, Contemporary Mathematics, Volume 671 (American Mathematical Society, Providence, RI, 2016).CrossRefGoogle Scholar
Evans, D. G. and Sims, A., When is the Cuntz–Krieger algebra of a higher-rank graph approximately finite-dimensional?, J. Funct. Anal. 263(1) (2012), 183–215.10.1016/j.jfa.2012.03.024CrossRefGoogle Scholar
Farah, I. and Rørdam, M., Axiomatizability of the stable rank of ${\rm C}^{*}$-algebras, Münster J. Math. 10(2) (2017), 269–275.Google Scholar
Hazlewood, R., Raeburn, I., Sims, A. and Webster, S. B. G., Remarks on some fundamental results about higher-rank graphs and their $C^{*}$-algebras, Proc. Edinb. Math. Soc. (2) 56(2) (2013), 575–597.CrossRefGoogle Scholar
Jeong, J. A., Stable rank and real rank of graph $C^{*}$-algebras, in Operator algebras and applications, pp. 97–106, Advanced Studies in Pure Mathematics, Volume 38 (Mathematical Society of Japan, Tokyo, 2004).Google Scholar
Jeong, J. A., Park, G. H. and Shin, D. Y., Stable rank and real rank of graph $C^{*}$-algebras, Pacific J. Math. 200(2) (2001), 331–343.CrossRefGoogle Scholar
Kirchberg, E., Exact $\textrm {C}^{*}$-algebras, tensor products, and the classification of purely infinite algebras. In Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Zürich, 1994), pp. 943–954 (Birkhäuser, Basel, 1995).CrossRefGoogle Scholar
Kirchberg, E. and Rørdam, M., Non-simple purely infinite $C^{*}$-algebras, Amer. J. Math. 122(3) (2000), 637–666.10.1353/ajm.2000.0021CrossRefGoogle Scholar
Kumjian, A. and Pask, D., Higher rank graph $C^{*}$-algebras, New York J. Math. 6 (2000), 1–20.Google Scholar
Kumjian, A., Pask, D. and Sims, A., $C^{*}$-algebras associated to coverings of $k$-graphs, Doc. Math. 13 (2008), 161–205.Google Scholar
Lewin, P. and Sims, A., Aperiodicity and cofinality for finitely aligned higher-rank graphs, Math. Proc. Cambridge Philos. Soc. 149(2) (2010), 333–350.CrossRefGoogle Scholar
Osaka, H. and Phillips, N. C., Stable and real rank for crossed products by automorphisms with the tracial Rokhlin property, Ergodic Theory Dynam. Syst. 26(5) (2006), 1579–1621.CrossRefGoogle Scholar
Pask, D., Quigg, J. and Raeburn, I., Coverings of $k$-graphs, J. Algebra 289(1) (2005), 161–191.10.1016/j.jalgebra.2005.01.051CrossRefGoogle Scholar
Pask, D., Raeburn, I., Rørdam, M. and Sims, A., Rank-two graphs whose $C^{*}$-algebras are direct limits of circle algebras, J. Funct. Anal. 239(1) (2006), 137–178.CrossRefGoogle Scholar
Pask, D., Rennie, A. and Sims, A., The noncommutative geometry of $k$-graph $C^{*}$-algebras, J. K-Theory 1(2) (2008), 259–304.CrossRefGoogle Scholar
Pask, D., Sierakowski, A. and Sims, A., Twisted $k$-graph algebras associated to Bratteli diagrams, Int. Eq. Oper. Theory 81(3) (2015), 375–408.CrossRefGoogle Scholar
Phillips, N. C., A classification theorem for nuclear purely infinite simple $C^{*}$-algebras, Doc. Math. 5 (2000), 49–114.Google Scholar
Putnam, I. F., On the topological stable rank of certain transformation group $C^{*}$-algebras, Ergodic Theory Dynam. Syst. 10(1) (1990), 197–207.CrossRefGoogle Scholar
Raeburn, I. and Sims, A., Product systems of graphs and the Toeplitz algebras of higher-rank graphs, J. Oper. Theory 53(2) (2005), 399–429.Google Scholar
Raeburn, I., Sims, A. and Yeend, T., Higher-rank graphs and their $C^{*}$-algebras, Proc. Edinb. Math. Soc. (2) 46(1) (2003), 99–115.CrossRefGoogle Scholar
Riedel, N., On the topological stable rank of irrational rotation algebras, J. Oper. Theory 13(1) (1985), 143–150.Google Scholar
Rieffel, M. A., Dimension and stable rank in the $K$-theory of $C^{\ast }$-algebras, Proc. London Math. Soc. (3) 46(2) (1983), 301–333.CrossRefGoogle Scholar
Robertson, D. and Sims, A., Simplicity of $C^{\ast }$-algebras associated to row-finite locally convex higher-rank graphs, Israel J. Math. 172 (2009), 171–192.CrossRefGoogle Scholar
Rørdam, M., The stable and the real rank of $\mathcal {Z}$-absorbing $C^{*}$-algebras, Internat. J. Math. 15(10) (2004), 1065–1084.CrossRefGoogle Scholar
Rørdam, M., Larsen, F. and Laustsen, N., An introduction to $K$-theory for $C^{*}$-algebras, London Mathematical Society Student Texts, Volume 49 (Cambridge University Press, Cambridge, 2000).Google Scholar
Rørdam, M. and Størmer, E., Classification of nuclear $C^{*}$-algebras. Entropy in operator algebras, Encyclopaedia of Mathematical Sciences, Volume 126 (Springer-Verlag, Berlin, 2002). Operator Algebras and Non-commutative Geometry, 7.10.1007/978-3-662-04825-2CrossRefGoogle Scholar
Ruiz, E., Sims, A. and Sørensen, A. P. W., UCT-Kirchberg algebras have nuclear dimension one, Adv. Math. 279 (2015), 1–28.CrossRefGoogle Scholar
Sato, Y., White, S. and Winter, W., Nuclear dimension and $\mathcal {Z}$-stability, Invent. Math. 202(2) (2015), 893–921.CrossRefGoogle Scholar
Schafhauser, C. P., Finiteness properties of certain topological graph algebras, Bull. Lond. Math. Soc. 47(3) (2015), 443–454.10.1112/blms/bdv012CrossRefGoogle Scholar
Sims, A., Gauge-invariant ideals in the $C^{*}$-algebras of finitely aligned higher-rank graphs, Canad. J. Math. 58(6) (2006), 1268–1290.CrossRefGoogle Scholar
Sims, A. and Williams, D. P., Amenability for Fell bundles over groupoids, Illinois J. Math. 57(2) (2013), 429–444.CrossRefGoogle Scholar
Suzuki, Y., Almost finiteness for general Étale Groupoids and its applications to stable rank of crossed products, Int. Math. Res. Not. IMRN 19 (2020), 6007–6041.CrossRefGoogle Scholar
Tomforde, M., The ordered $K_0$-group of a graph $C^{*}$-algebra, C. R. Math. Acad. Sci. Soc. R. Can. 25(1) (2003), 19–25.Google Scholar
Villadsen, J., On the stable rank of simple $C^{\ast }$-algebras, J. Amer. Math. Soc. 12(4) (1999), 1091–1102.CrossRefGoogle Scholar