Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Pavlovic, Miroslav
2014.
Definition and Properties of the Libera Operator on Mixed Norm Spaces.
The Scientific World Journal,
Vol. 2014,
Issue. ,
p.
1.
Chatzifountas, Christos
Girela, Daniel
and
Peláez, José Ángel
2014.
A generalized Hilbert matrix acting on Hardy spaces.
Journal of Mathematical Analysis and Applications,
Vol. 413,
Issue. 1,
p.
154.
Constantin, Olivia
and
Peláez, José Ángel
2015.
Boundedness of the Bergman projection on Lp-spaces with exponential weights.
Bulletin des Sciences Mathématiques,
Vol. 139,
Issue. 3,
p.
245.
Jevtić, Miroljub
Vukotić, Dragan
and
Arsenović, Miloš
2016.
Taylor Coefficients and Coefficient Multipliers of Hardy and Bergman-Type Spaces.
Vol. 2,
Issue. ,
p.
107.
Mleczko, Paweł
2016.
Hadamard Multipliers and Abel Dual of Hardy Spaces.
Journal of Function Spaces,
Vol. 2016,
Issue. ,
p.
1.
Jevtić, Miroljub
Vukotić, Dragan
and
Arsenović, Miloš
2016.
Taylor Coefficients and Coefficient Multipliers of Hardy and Bergman-Type Spaces.
Vol. 2,
Issue. ,
p.
179.
Popa, N.
2017.
Order Structures in Banach Spaces of Analytic Functions.
Complex Analysis and Operator Theory,
Vol. 11,
Issue. 8,
p.
1765.
Girela, Daniel
and
Merchán, Noel
2017.
A Hankel Matrix Acting on Spaces of Analytic Functions.
Integral Equations and Operator Theory,
Vol. 89,
Issue. 4,
p.
581.
Merchán, Noel
2019.
Mean Lipschitz spaces and a generalized Hilbert operator.
Collectanea Mathematica,
Vol. 70,
Issue. 1,
p.
59.
Blasco, O.
and
García-Bayona, I.
2020.
On the Taylor Coefficients of Functions in the Hardy Space Over the Bidisc.
Complex Analysis and Operator Theory,
Vol. 14,
Issue. 6,
Liu, Chao
2020.
Multipliers for Dirichlet type spaces by randomization.
Banach Journal of Mathematical Analysis,
Vol. 14,
Issue. 3,
p.
935.
Peláez, José Ángel
and
de la Rosa, Elena
2021.
Hilbert-type operator induced by radial weight.
Journal of Mathematical Analysis and Applications,
Vol. 495,
Issue. 1,
p.
124689.
Peláez, José Ángel
Rättyä, Jouni
and
Wu, Fanglei
2022.
Integral Operators Induced by Symbols with Non-negative Maclaurin Coefficients Mapping into $$H^\infty $$.
The Journal of Geometric Analysis,
Vol. 32,
Issue. 5,
Peláez, José Ángel
Rättyä, Jouni
and
Wu, Fanglei
2023.
Volterra-type operators mapping weighted Dirichlet space into $$H^\infty $$.
Mathematische Zeitschrift,
Vol. 304,
Issue. 2,
Sun, Fangmei
and
Ye, Fangqin
2023.
Characterizations of Hankel type measures.
Journal of Mathematical Analysis and Applications,
Vol. 527,
Issue. 1,
p.
127434.
Tang, Pengcheng
and
Zhang, Xuejun
2023.
Generalized integral type Hilbert operator acting between weighted Bloch spaces.
Mathematical Methods in the Applied Sciences,
Vol. 46,
Issue. 17,
p.
18458.
Blasco, Oscar
2024.
Cesàro-type operators on Hardy spaces.
Journal of Mathematical Analysis and Applications,
Vol. 529,
Issue. 2,
p.
127017.
Tang, Pengcheng
2025.
Hilbert type operators acting from the Bloch space into Bergman spaces.
Proceedings of the Edinburgh Mathematical Society,
Vol. 68,
Issue. 1,
p.
205.
Das, Suman
Huang, Jie
and
Rasila, Antti
2025.
Zygmund’s Theorem for Harmonic Quasiregular Mappings.
Complex Analysis and Operator Theory,
Vol. 19,
Issue. 5,
Lv, Xiaofen
Wang, Lei
and
Tang, Xiaomin
2025.
p-Hankel matrices on Dirichlet-type spaces.
Banach Journal of Mathematical Analysis,
Vol. 19,
Issue. 3,
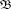 1(⊂ H1), of the Bloch space. Assertion (1) extends the Hardy–Littlewood theorem, which says the following.
1(⊂ H1), of the Bloch space. Assertion (1) extends the Hardy–Littlewood theorem, which says the following.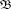 1 into H1.
1 into H1.
