Hostname: page-component-76c49bb84f-229nc Total loading time: 0 Render date: 2025-07-05T17:22:14.454Z Has data issue: false hasContentIssue false
  • English
  • Français

Cesàro-type operators on Bergman–Morrey spaces and Dirichlet–Morrey spaces

Part of: Other generalizations Spaces and algebras of analytic functions Special classes of linear operators

Published online by Cambridge University Press:  26 November 2024

Huayou Xie ,
Qingze Lin  and
Junming Liu
Huayou Xie
Affiliation:
Department of Mathematics, Sun Yat-sen University, Guangzhou, 510275, P.R. China
Qingze Lin
Affiliation:
Department of Mathematics, Shantou University, Shantou, 515063, P.R. China
Junming Liu*
Affiliation:
School of Mathematics and Statistics, Guangdong University of Technology, Guangzhou, 510520, P.R. China
*
Corresponding author: Junming Liu, email: jmliu@gdut.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we will show the Carleson measure characterizations for the boundedness and compactness of the Cesàro-type operator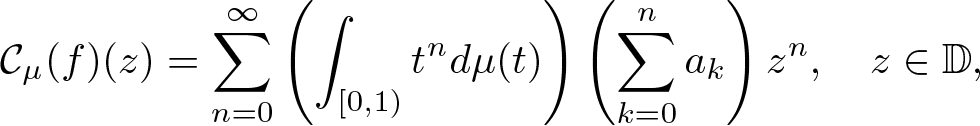

\begin{equation*}\mathcal{C}_{\mu}(f)(z)=\sum^{\infty}_{n=0}\left( \int_{[0,1)}t^nd\mu(t)\right) \left(\sum^{n}_{k=0}a_k \right)z^n, \quad z\in \mathbb{D},\end{equation*}

acting on a number of important analytic function spaces on $\mathbb{D}$, where µ is a positive finite Borel measure. The function spaces are some newly appeared analytic function spaces (e.g., Bergman–Morrey spaces 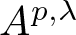$A^{p,\lambda}$ and Dirichlet–Morrey spaces 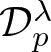$\mathcal{D}_p^{\lambda}$) . This work continues the lines of the previous characterizations by Blasco and Galanopoulos et al. for classical Hardy spaces and weighted Bergman spaces and so forth.

Keywords

Cesàro-type operatorsBergman–Morrey spacesDirichlet–Morrey spacesboundednesscompactness

MSC classification

Primary: 47B38: Operators on function spaces (general)
Secondary: 30H05: Bounded analytic functions 31C25: Dirichlet spaces

Information

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 68 , Issue 1 , February 2025 , pp. 268 - 299
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abadias, L. and Miana, P. J., Generalized Cesáro operators, fractional finite differences and gamma functions, J. Funct. Anal. 274(5) (2018), 1424–1465.CrossRefGoogle Scholar
Adams, D. R. and Xiao, J., Nonlinear potential analysis on Morrey spaces and their capacities, Indiana Univ. Math. J. 53(6) (2004), 1629–1663.CrossRefGoogle Scholar
Adams, D. R. and Xiao, J., Morrey spaces in harmonic analysis, Ark. Mat. 50(2) (2012), 201–230.CrossRefGoogle Scholar
Agrawal, M. R., Howlett, P. G., Lucas, S. K., Naik, S. and Ponnusamy, S., Boundedness of generalized Cesáro averaging operators on certain function spaces, J. Comput. Appl. Math. 180(2) (2005), 333–344.CrossRefGoogle Scholar
Andersen, K. F., Cesáro averaging operators on Hardy spaces, Proc. Roy. Soc. Edinburgh Sect. A 126(3) (1996), 617–624.CrossRefGoogle Scholar
Andersen, K. F., Boundedness of the Cesáro averaging operators on Dirichlet spaces, Proc. Roy. Soc. Edinburgh Sect. A 134(4) (2004), 609–616.CrossRefGoogle Scholar
Bao, G., Sun, F. and Wulan, H., Carleson measures and the range of a Cesáro-like operator acting on $H^\infty$, Anal. Math. Phys. 12(6) (2022), .CrossRefGoogle Scholar
Blasco, O., Operators on weighted Bergman spaces $(0 \lt p\leq1)$ and applications, Duke Math. J. 66(3) (1992), 443–467.CrossRefGoogle Scholar
Blasco, O., Cesáro-type operators on Hardy spaces, J. Math. Anal. Appl. 529(2) (2024), .CrossRefGoogle Scholar
Borgohain, D. and Naik, S., Generalized Cesáro operators on the spaces of Cauchy transforms, Acta Sci. Math. (Szeged) 83(1-2) (2017), 143–154.CrossRefGoogle Scholar
Bourdon, P. S., Shapiro, J. H. and Sledd, W. T., Fourier series, mean Lipschitz spaces, and bounded mean oscillation, Analysis at Urbana I, London Math. Soc. Lecture Note Ser., Volume 137, (Cambridge Univ. Press, Cambridge, 1989).Google Scholar
Carleson, L., An interpolation problem for bounded analytic functions, Amer. J. Math. 80 (2) (1958), 921–930.CrossRefGoogle Scholar
Carleson, L., Interpolations by bounded analytic functions and the corona problem, Ann. of Math. 76 (3) (1962), 547–559.CrossRefGoogle Scholar
Duong, X. T., Xiao, J. and Yan, L., Old and new Morrey spaces with heat kernel bounds, J. Fourier Anal. Appl. 13(1) (2007), 87–111.CrossRefGoogle Scholar
Galanopoulos, P., The Cesáro operator on Dirichlet spaces, Acta Sci. Math. (Szeged) 67(1-2) (2001), 411–420.Google Scholar
Galanopoulos, P., Girela, D., Mas, A. and Merchán, N., Operators induced by radial measures acting on the Dirichlet space, Results Math. 78(3) (2023), .CrossRefGoogle Scholar
Galanopoulos, P., Girela, D. and Merchán, N., Cesáro-like operators acting on spaces of analytic functions, Anal. Math. Phys. 12(2) (2022), .CrossRefGoogle Scholar
Galanopoulos, P., Girela, D. and Merchán, N., Cesáro-type operators associated with Borel measures on the unit disc acting on some Hilbert spaces of analytic functions, J. Math. Anal. Appl. 526(2) (2023), .CrossRefGoogle Scholar
Galanopoulos, P., Merchán, N. and Siskakis, A. G., A family of Dirichlet-Morrey spaces, Complex Var. Elliptic Equ. 64(10) (2019), 1686–1702.CrossRefGoogle Scholar
Galanopoulos, P., Merchán, N. and Siskakis, A. G., Semigroups of composition operators in analytic Morrey spaces, Integral Equations Operator Theory, 92(2) (2020), CrossRefGoogle Scholar
Hardy, G. H., Note on a theorem of Hilbert, Math. Z. 6(3-4) (1920), 314–317.CrossRefGoogle Scholar
Hardy, G. H., Notes on some points in the integral calculus LXVI: the arithmetic mean of a Fourier constant, Messenger Math. 58(3–4) (1929), 50–52.Google Scholar
Hastings, W. W., A Carleson measure theorem for Bergman spaces, Proc. Amer. Math. Soc. 52 (1) (1975), 237–241.CrossRefGoogle Scholar
Hu, L., Li, S. and Yang, R., Corona and Wolff theorems for the multiplier algebra of Dirichlet-Morrey spaces, Canad. Math. Bull. 65(4) (2022), 963–975.CrossRefGoogle Scholar
Jin, J. and Tang, S., Generalized Cesáro operators on Dirichlet-type spaces, Acta Math. Sci. Ser. B (Engl. Ed.) 42(1) (2022), 212–220.Google Scholar
Kozono, H. and Yamazaki, M., The stability of small stationary solutions in Morrey spaces of the Navier-Stokes equation, Indiana Univ. Math. J. 44(4) (1995), 1307–1336.CrossRefGoogle Scholar
Kukavica, I., Regularity for the Navier-Stokes equations with a solution in a Morrey space, Indiana Univ. Math. J. 57(6) (2008), 2843–2860.CrossRefGoogle Scholar
Landau, E., A note on a theorem of series of positive terms: extract from a letter, from Prof. E. Landau to Prof. I. Shur (communicated by G. Hardy), J. London Math. Soc. 1 (1) (1926), 38–39.CrossRefGoogle Scholar
Lemarié-Rieusset, P. G., The Navier-Stokes equations in the critical Morrey-Campanato space, Rev. Mat. Iberoam. 23(3) (2007), 897–930.CrossRefGoogle Scholar
Lemarié-Rieusset, P. G., Multipliers and Morrey spaces, Potential Anal. 38(3) (2013), 741–752.CrossRefGoogle Scholar
Liu, J. and Lou, Z., Carleson measure for analytic Morrey spaces, Nonlinear Anal. 125 (13) (2015), 423–432.CrossRefGoogle Scholar
Liu, J. and Lou, Z., Properties of analytic Morrey spaces and applications, Math. Nachr. 288(14–15) (2015), 1673–1693.CrossRefGoogle Scholar
MacCluer, B. and Zhao, R., Vanishing logarithmic Carleson measures, Illinois J. Math. 46(2) (2002), 507–518.CrossRefGoogle Scholar
Miao, J., The Cesáro operator is bounded on Hp for $0 \lt p \lt 1$, Proc. Amer. Math. Soc. 116(4) (1992), 1077–1079.Google Scholar
Morrey, C. B., On the solutions of quasi-linear elliptic partial differential equations, Trans. Amer. Math. Soc. 43(1) (1938), 126–166.CrossRefGoogle Scholar
Naik, S., Generalized Cesáro operators on certain function spaces, Ann. Polon. Math. 98(2) (2010), 189–199.CrossRefGoogle Scholar
Ohno, S., Stroethoff, K. and Zhao, R., Weighted composition operators between Bloch-type spaces, The Rocky Mountain Journal of Mathematics 33 (1) (2003), 191–215.CrossRefGoogle Scholar
Olsen, P. A., Fractional integration, Morrey spaces and a Schrödinger equation, Comm. Partial Differential Equations. 20(11–12) (1995), 2005–2055.CrossRefGoogle Scholar
Ortega, J. M. and Fábrega, J., Pointwise multipliers and corona type decomposition in BMOA, Ann. Inst. Fourier (Grenoble) 46(1) (1996), 111–137.CrossRefGoogle Scholar
Palagachev, D. K. and Softova, L. G., Singular integral operators, Morrey spaces and fine regularity of solutions to PDE’s, Potential Anal. 20(3) (2004), 237–263.CrossRefGoogle Scholar
Pinchover, Y. and Psaradakis, G., On positive solutions of the (p, A)-Laplacian with potential in Morrey space, Anal. PDE 9(6) (2016), 1317–1358.CrossRefGoogle Scholar
Siskakis, A. G., Composition semigroups and the Cesáro operator on Hp, J. London Math. Soc. 36(1) (1987), 153–164.CrossRefGoogle Scholar
Siskakis, A. G., The Cesáro operator is bounded on H 1, Proc. Amer. Math. Soc. 110(2) (1990), 461–462.Google Scholar
Siskakis, A. G., On the Bergman space norm of the Cesáro operator, Arch. Math. (Basel) 67(4) (1996), 312–318.CrossRefGoogle Scholar
Souplet, P., Morrey spaces and classification of global solutions for a supercritical semilinear heat equation in $\mathbb{R}^n$, J. Funct. Anal. 272(5) (2017), 2005–2037.CrossRefGoogle Scholar
Stempak, K., Cesáro averaging operators, Proc. Roy. Soc. Edinburgh Sect. A 124(1) (1994), 121–126.CrossRefGoogle Scholar
Stević, S., Cesáro averaging operators, Math. Nachr. 248(249) (2003), 185–189.CrossRefGoogle Scholar
Stević, S., The generalized Cesáro operator on Dirichlet spaces, Studia Sci. Math. Hungar. 40(1–2) (2003), 83–94.Google Scholar
Sun, F., Ye, F. and Zhou, L., A Cesáro-like operator from Besov spaces to some spaces of analytic functions. arXiv:2305.02717, 2023.Google Scholar
Tang, P., Cesáro-like operators acting on a class of analytic function spaces, Anal. Math. Phys. 13 (6) (2023), 96.CrossRefGoogle Scholar
Taylor, M. E., Analysis on Morrey spaces and applications to Navier-Stokes and other evolution equations, Comm. Partial Differential Equations. 17(9–10) (1992), 1407–1456.CrossRefGoogle Scholar
Wakabayashi, F., The Keller-Segel system of parabolic-parabolic type in Morrey space, J. Differential Equations 265(9) (2018), 4661–4686.CrossRefGoogle Scholar
Wulan, H. and Zhou, J., Q_{K} and Morrey type spaces, Ann. Acad. Sci. Fenn. Math. 38(1) (2013), 193–207.CrossRefGoogle Scholar
Wu, Z. and Xie, C., Q spaces and Morrey spaces, J. Funct. Anal. 201(1) (2003), 282–297.CrossRefGoogle Scholar
Yang, Y. and Liu, J., Integral operators on Bergman-Morrey spaces, J. Geom. Anal. 32(6) (2022), .CrossRefGoogle Scholar
Zhao, R., On logarithmic Carleson measures, Acta Sci. Math. (Szeged) 69(3–4) (2003), 605–618.Google Scholar
Zhu, K., Bloch type spaces of analytic functions, Rocky Mountain J. Math. 23(3) (1993), 1143–1177.CrossRefGoogle Scholar
Zhu, K., Operator Theory in Function Spaces, Mathematical Surveys and Monographs, Second edition, Volume 138 (Amer. Math. Soc., Providence, 2007).CrossRefGoogle Scholar
Zhu, X., Qian, R. and Hu, N., Embedding and Volterra integral operators from Dirichlet-Morrey spaces into general function spaces, Complex Var. Elliptic Equ. 67(9) (2022), 2303–2317.CrossRefGoogle Scholar