Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Beardone, Alan F.
2001.
Continued Fractions, Discrete Groups and Complex Dynamics.
Computational Methods and Function Theory,
Vol. 1,
Issue. 2,
p.
535.

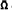 of Ω is also such a convergence set. Actually, we prove more: every continued fraction
of Ω is also such a convergence set. Actually, we prove more: every continued fraction 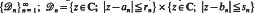 where
where 
