Hostname: page-component-cb9f654ff-5jtmz Total loading time: 0 Render date: 2025-08-03T01:46:30.985Z Has data issue: false hasContentIssue false
  • English
  • Français

The fibred product near-rings and near-ring modules for certain categories

Published online by Cambridge University Press:  20 January 2009

James R. Clay
James R. Clay
Affiliation:
University of Arizona Tucson, Arizona 85721 USA
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In somes categories, there are structures that look very much like groups, and they usually are. These structures are called group-objects and were first studied by Eckmann and Hilton (1). If our category 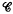has an object T such that hom(X, T)= {tx}, a singleton, for each object X ∈ Ob 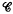, T is called a terminal object. Our category 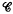must have products; i.e. for A1,…, An ∈;. Ob 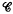, there is an object A1 × … × An ∈ Ob 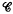and morphisms pi: A1 × … × An → Ai so that if fi: X → Ai, i = 1, 2, …, n, are morphisms of 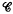, then there is a unique morphism [f1, …, fn]: X → A1 × … × An such that 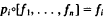for i = 1, 2, …, n.

Information

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 23 , Issue 1 , February 1980 , pp. 15 - 25
Copyright
Copyright © Edinburgh Mathematical Society 1980

References

REFERENCES

(1) Eckmann, B. and Hilton, P. J., Group-like structures in general categories I: Multiplications and comultiplications, Math. Ann. 145 (1962), 227–255.CrossRefGoogle Scholar
(2) Eckmann, B. and Hilton, P. J., Group-like structures in general categories II: Equalizers, limits, lengths, Math. Ann. 151 (1963), 150–186.Google Scholar
(3) Eckmann, B. and Hilton, P. J., Group-like structures in general categories III: Primitive categories, Math Ann. 150 (1963), 165–187.CrossRefGoogle Scholar
(4) Fröhlich, A., Distributively generated near-rings I. Ideal theory, Proc. London Math. Soc. 8 (1958), 76–94.CrossRefGoogle Scholar
(5) Gonshor, H., On abstract affine near-rings, Pacific J. Math. 14 (1964), 1237–1240.Google Scholar
(6) Holcombe, M., Categorical representations of endomorphism near-rings, J. London Math. Soc. (2) 16 (1977), 21–37.CrossRefGoogle Scholar
(7) Maclane, S., Homology (Springer-Verlag, Berlin, 1963).CrossRefGoogle Scholar
(8) Maclane, S. and Birkoff, G., Algebra (Macmillan, New York, 1967).Google Scholar
(9) Rotman, J., The theory of groups: an introduction (Allyn and Bacon, Boston, 1965).Google Scholar