Article contents
The “Fourier” Theory of the Cardinal Function
Published online by Cambridge University Press: 20 January 2009
Extract
The generalised Riesz-Fischer theorem states that if
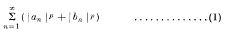
is convergent, with 1 < p ≤ 2, then

is the Fourier series of a function of class 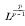 . When p > 2 the series (2) is not necessarily a Fourier series; neither is it necessarily a Fourier D-series. It will be shown below that it must however be what may be called a “Fourier Stieltjes” series. That is to say, the condition (1) with (p > 1) implies that there is a continuous function F (x) such that
. When p > 2 the series (2) is not necessarily a Fourier series; neither is it necessarily a Fourier D-series. It will be shown below that it must however be what may be called a “Fourier Stieltjes” series. That is to say, the condition (1) with (p > 1) implies that there is a continuous function F (x) such that
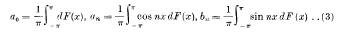
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1928
References
page 169 note 1 Hobson, . Functions of a Real Variable (1926), vol. II., p. 599.Google Scholar
page 19 note 2 ibid., p. 488.
page 170 note 1 CfHobson, . loc. cit., vol. I., p. 506.Google Scholar
page 172 note 1 Monatshefte für Math. u. Physik, 32 (1922), 84.Google Scholar
page 172 note 2 Hobson, . loc. cit., vol. II., pp. 560, 580.Google Scholar
page 172 note 3 cf. sec. 3.Google Scholar
page 173 note 1 By a theorem due to Hyslop, Proc. Edin. Math. Soc., 44 (1926), 79.Google Scholar
page 174 note 1 This process is legitimate, cfHobson, , loc. cit., p. 582.Google Scholar
page 174 note 2 Proc. Land. Math. Soc., 2, 26 (1926), 12.Google ScholarProc. Camb. Phil. Soc., 23 (1926), 373.CrossRefGoogle ScholarSee also Miss Grimshaw, M. E., “A case of distinction between Fourier integrals and Fourier series”, loc. cit., p. 755.Google Scholar
page 174 note 3 Bull, de I'Acad. Roy. de Belg. (Clause de Sciences) (1908), pp. 319–410 esp. p. 341.Google Scholar
page 176 note 1 Proc. Lond. Math. Soc. (2), 26 (1926), 1.Google Scholar
- 83
- Cited by

