Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-18T10:49:21.065Z Has data issue: false hasContentIssue false
  • English
  • Français

Freudenthal's theorem and spherical classes in H*QS0

Part of: Homotopy groups Homotopy theory

Published online by Cambridge University Press:  20 December 2019

Hadi Zare
Hadi Zare*
Affiliation:
College of Science, University of Tehran, Tehran, Iranhadi.zare@ut.ac.ir
Get access Rights & Permissions [Opens in a new window]

Abstract

This note is on spherical classes in 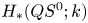$H_*(QS^0;k)$ when 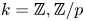$k=\mathbb{Z}, \mathbb{Z}/p$, with a special focus on the case of p=2 related to the Curtis conjecture. We apply Freudenthal's theorem to prove a vanishing result for the unstable Hurewicz image of elements in 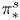${\pi _*^s}$ that factor through certain finite spectra. After either p-localization or p-completion, this immediately implies that elements of well-known infinite families in 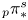${_p\pi _*^s}$, such as Mahowaldean families, map trivially under the unstable Hurewicz homomorphism 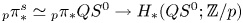${_p\pi _*^s}\simeq {_p\pi _*}QS^0\to H_*(QS^0;\mathbb{Z} /p)$. We also observe that the image of the submodule of decomposable elements under the integral unstable Hurewicz homomorphism 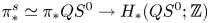$\pi _*^s\simeq \pi _*QS^0\to H_*(QS^0;\mathbb{Z} )$ is given by 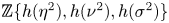$\mathbb{Z} \{h(\eta ^2),h(\nu ^2),h(\sigma ^2)\}$. We apply the latter to completely determine spherical classes in 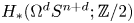$H_*(\Omega ^dS^{n+d};\mathbb{Z} /2)$ for certain values of n>0 and d>0; this verifies Eccles' conjecture on spherical classes in 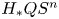$H_*QS^n$, n>0, on finite loop spaces associated with spheres.

Keywords

Freudenthal's theoreminfinite loop spacesHurewicz homomorphism

MSC classification

Primary: 55Q45: Stable homotopy of spheres 55P42: Stable homotopy theory, spectra
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 2 , May 2020 , pp. 323 - 341
Copyright
Copyright © Edinburgh Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Adams, J. F., On the non-existence of elements of Hopf invariant one, Ann. of Math. (2) 72 (1960), 20–104.CrossRefGoogle Scholar
2Asadi-Golmankhaneh, M. A. and Eccles, P. J., Double point self-intersection surfaces of immersions, Geom. Topol. 4 (2000), 149–170.CrossRefGoogle Scholar
3Barratt, M. G. and Eccles, P. J., Γ+-structures. I: a free group functor for stable homotopy theory, Topology 13 (1974), 25–45.CrossRefGoogle Scholar
4Boardman, J. M. and Steer, B., On Hopf invariants, Comment. Math. Helv. 42 (1967), 180–221.CrossRefGoogle Scholar
5Bousfield, A. K., K-localizations and K-equivalences of infinite loop spaces, Proc. Lond. Math. Soc. (3) 44(2) (1982), 291–311.CrossRefGoogle Scholar
6Bousfield, A. K. and Kan, D. M., Homotopy limits, completions and localizations, Lecture Notes in Mathematics, Volume 304 (Springer-Verlag, Berlin–New York, 1972).CrossRefGoogle Scholar
7Brown, E. H. Jr. and Gitler, S., A spectrum whose cohomology is a certain cyclic module over the Steenrod algebra, Topology 12 (1973), 283–295.CrossRefGoogle Scholar
8Brown, E. H. Jr. and Peterson, F. P., On the stable decomposition of Ω2S r + 2, Trans. Am. Math. Soc. 243 (1978), 287–298.CrossRefGoogle Scholar
9Curtis, E. B., The Dyer–Lashof algebra and the Λ-algebra, Ill. J. Math. 19 (1975), 231–246.CrossRefGoogle Scholar
10Eccles, P. J., Codimension one immersions and the Kervaire invariant one problem, Math. Proc. Cambridge Philos. Soc. 90 (1981), 483–493.CrossRefGoogle Scholar
11Harper, J. R., Secondary cohomology operations (American Mathematical Society, Providence, RI, 2002).Google Scholar
12Hu'ng, N. H. V., Erratum to: ‘Spherical classes and the algebraic transfer’, Trans. Am. Math. Soc. 355(9) (2003), 3841–3842.CrossRefGoogle Scholar
13Hu'ng, N. H. V. and Peterson, F. P., Spherical classes and the Dickson algebra, Math. Proc. Cambridge Philos. Soc. 124(2) (1998), 253–264.CrossRefGoogle Scholar
14Hunter, D. J. and Kuhn, N. J., Mahowaldean families of elements in stable homotopy groups revisited, Math. Proc. Cambridge Philos. Soc. 127(2) (1999), 237–251.CrossRefGoogle Scholar
15James, I. M., Reduced product spaces, Ann. Math. (2) 62 (1955), 170–197.CrossRefGoogle Scholar
16Kuhn, N. J., Constructions of families of elements in the stable homotopy groups of spheres, in Topology and representation theory (Evanston, IL, 1992). Contemporary Mathematics, Volume 158, pp. 135–155 (American Mathematical Society, Providence, RI, 1994).Google Scholar
17Lin, W. H., Some elements in the stable homotopy of spheres, Proc. Amer. Math. Soc. 95(2) (1985), 295–298.CrossRefGoogle Scholar
18Lin, W. H., Some infinite families in the stable homotopy of spheres, Math. Proc. Cambridge Philos. Soc. 101(3) (1987), 477–485.CrossRefGoogle Scholar
19Lin, W. H., An infinite family in $_2\pi ^{\rm s}_*$ at Adams filtration seven, Trans. Amer. Math. Soc. 328(1) (1991), 133–149.Google Scholar
20Mahowald, M., A new infinite family in $_2\pi ^s_*$, Topology 16 (1977), 249–256.CrossRefGoogle Scholar
21May, J. P., The geometry of iterated loop spaces, Lecture Notes in Mathematics, Volume 271 (Springer-Verlag, Berlin–Heidelberg–New York, 1972).CrossRefGoogle Scholar
22Mosher, R. E. and Tangora, M. C., Cohomology operations and applications in homotopy theory, Harper's Series in Modern Mathematics (Harper and Row, New York–Evanston–London, 1968).Google Scholar
23Ravenel, D. C., Nilpotence and periodicity in stable homotopy theory (Princeton University Press, Princeton, NJ, 1992).Google Scholar
24Snaith, V. P., A stable decomposition of ΩnS nX, J. Lond. Math. Soc. II. Ser. 7 (1974), 577–583.CrossRefGoogle Scholar
25Wellington, R. J., The unstable Adams spectral sequence for free iterated loop spaces, Mem. Am. Math. Soc. 36(258) (1982), 225.Google Scholar
26Zare, H., On the Hurewicz homomorphism on the extensions of ideals in $\pi _*^s$ and spherical classes in $H_*Q_0S^0$ (arXiv:1504.06752, 2015).Google Scholar
27Zare, H., Spherical classes in some finite loop spaces of spheres, Topology Appl. 224 (2017), 1–18.CrossRefGoogle Scholar