Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Castravet, Ana-Maria
and
Tevelev, Jenia
2015.
M ¯ 0 , n is not a Mori dream space.
Duke Mathematical Journal,
Vol. 164,
Issue. 8,
Belkale, Prakash
Gibney, Angela
and
Kazanova, Anna
2016.
Scaling of conformal blocks and generalized theta functions over $$\overline{\mathcal {M}}_{g,n}$$ M ¯ g , n.
Mathematische Zeitschrift,
Vol. 284,
Issue. 3-4,
p.
961.
Kazanova, Anna
2016.
On S n -invariant conformal blocks vector bundles of rank one on $${\overline{M}_{0,n}}$$ M ¯ 0 , n.
Manuscripta Mathematica,
Vol. 149,
Issue. 1-2,
p.
107.
Mukhopadhyay, Swarnava
2016.
Rank-level duality and conformal block divisors.
Advances in Mathematics,
Vol. 287,
Issue. ,
p.
389.
Swinarski, David
2018.
Software for computing conformal block divisors
on M0,n.
Journal of Software for Algebra and Geometry,
Vol. 8,
Issue. 1,
p.
81.
Moon, Han-Bom
and
Swinarski, David
2019.
On the S-invariant F-conjecture.
Journal of Algebra,
Vol. 517,
Issue. ,
p.
439.
Hobson, Natalie L. F.
2019.
Quantum Kostka and the rank one problem for 𝔰𝔩2m
.
Advances in Geometry,
Vol. 19,
Issue. 1,
p.
71.
Damiolini, Chiara
Gibney, Angela
and
Tarasca, Nicola
2021.
Conformal blocks from vertex algebras and their
connections on ℳg,n.
Geometry & Topology,
Vol. 25,
Issue. 5,
p.
2235.
Chen, L.
Gibney, A.
Heller, L.
Kalashnikov, E.
Larson, H.
and
Xu, W.
2024.
On an Equivalence of Divisors on $\overline {\text {M}}_{0,n}$ from Gromov-Witten Theory and Conformal Blocks.
Transformation Groups,
Vol. 29,
Issue. 2,
p.
561.
Belkale, Prakash
and
Fakhruddin, Najmuddin
2025.
Perspectives on Four Decades of Algebraic Geometry, Volume 1.
Vol. 351,
Issue. ,
p.
263.

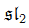 Conformal Blocks Divisors on
Conformal Blocks Divisors on