Hostname: page-component-7479d7b7d-8zxtt Total loading time: 0 Render date: 2024-07-12T23:31:14.634Z Has data issue: false hasContentIssue false
  • English
  • Français

A New Class of Maximal Triangular Algebras

Part of: Linear spaces and algebras of operators

Published online by Cambridge University Press:  03 May 2018

John Lindsay Orr
John Lindsay Orr*
Affiliation:
Toll House, Traquair Road, Innerleithen EH44 6PF, UKme@johnorr.us
Get access Rights & Permissions [Opens in a new window]

Abstract

Triangular algebras, and maximal triangular algebras in particular, have been objects of interest for over 50 years. Rich families of examples have been studied in the context of many w*- and C*-algebras, but there remains a dearth of concrete examples in 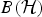$B({\cal H})$. In previous work, we described a family of maximal triangular algebras of finite multiplicity. Here, we investigate a related family of maximal triangular algebras with infinite multiplicity, and unearth a new asymptotic structure exhibited by these algebras.

Keywords

triangular algebranest algebrainfinite multiplicity

MSC classification

Primary: 47L35: Nest algebras, CSL algebras 47L75: Other nonselfadjoint operator algebras
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 61 , Issue 4 , November 2018 , pp. 909 - 931
Copyright
Copyright © Edinburgh Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Davidson, K. R., Similarity and compact perturbations of nest algebras, J. Reine Angew. Math. 348 (1984), 286–294.Google Scholar
2Davidson, K. R., Nest algebras (eds Brezis, H., Douglas, R. G. and Jeffrey, A.), Research Notes in Mathematics, Volume 191, pp. 1–412 (Pitman, Boston, MA, 1988).Google Scholar
3Erdos, J. A., Unitary invariants for nests, Pacific J. Math. 23 (1967), 229–256.Google Scholar
4Kadison, R. V., Triangular algebras–another chapter, In Selfadjoint and nonselfadjoint operator algebras and operator theory (ed. Doran, R. S.), Contemporary Mathematics, Volume 120, pp. 63–76 (CBMS), (American Mathematical Society, 1991).Google Scholar
5Kadison, R. V. and Singer, I. M., Extensions of pure states, Amer. J. Math. 81 (1959), 383–400.Google Scholar
6Kadison, R. V. and Singer, I. M., Triangular operator algebras, Amer. J. Math. 82(2) (1960), 227–259.Google Scholar
7Larson, D. R., Nest algebras and similarity transformations, Ann. Math. 121 (1985), 409–427.Google Scholar
8Muhly, P. S., Saito, K.-S. and Solel, B., Coordinates for triangular operator algebras, Ann. of Math. (2) 127 (1988), 245–278.Google Scholar
9Muhly, P. S. and Solel, B., Subalgebras of groupoid C*-algebras, J. Reine Angew. Math. 402 (1989), 41–75.Google Scholar
10Orr, J. L., On the closure of triangular algebras, Amer. J. Math. 112 (1990), 481–497.Google Scholar
11Orr, J. L., An estimate on the norm of the product of infinite block operator matrices, J. Combin. Theory Ser. A 63(2) (1993), 195–209.Google Scholar
12Orr, J. L., The maximal ideals of a nest algebra, J. Func. Anal. 124 (1994), 119–134.Google Scholar
13Orr, J. L., Triangular algebras and ideals of nest algebras, Mem. Amer. Math. Soc. 117(562) 1995, 49pp.Google Scholar
14Orr, J. L., The stable ideals of a continuous nest algebra, J. Operator Theory 45 (2001), 377–412.Google Scholar
15Peters, J. R., Poon, Y. T. and Wagner, B. H., Triangular AF algebras, J. Operator Theory 23(1) (1990), 81–114.Google Scholar
16Poon, Y. T., Maximal triangular subalgebras need not be closed, Proc. Amer. Math. Soc. (1991), 475–479.Google Scholar
17Power, S. C., The classification of triangular subalgebras of AF C*-algebras, Bull. Lond. Math. Soc. 22(3) (1990), 269–272.Google Scholar
18Ringrose, J. R., On some algebras of operators, Proc. London Math. Soc. 15(3) (1965), 61–83.Google Scholar
19Solel, B., Irreducible triangular algebras, Volume 290 (American Mathematical Society, 1984).Google Scholar