Hostname: page-component-7dd5485656-glrdx Total loading time: 0 Render date: 2025-10-31T01:50:01.192Z Has data issue: false hasContentIssue false
  • English
  • Français

On Kilmister's Conditions for the Existence of Linear Integrals of Dynamical Systems

Published online by Cambridge University Press:  20 January 2009

R. H. Boyer
R. H. Boyer
Affiliation:
Department of Applied Mathematics, University of Liverpool
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Kilmister (1) has considered dynamical systems specified by coordinates q( = 1, 2, , n) and a Lagrangian

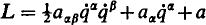
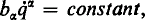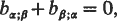
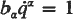(with summation convention). He sought to determine generally covariant conditions for the existence of a first integral, , linear in the velocities. He showed that it is not, as is usually stated, necessary that there must exist an ignorable coordinate (equivalently, that b must be a Killing field:

where covariant derivation is with respect to a). On the contrary, a singular integral, in the sense that for all time if satisfied initially, need not be accompanied by an ignorable coordinate.

Information

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 14 , Issue 3 , June 1965 , pp. 243 - 244
Copyright
Copyright Edinburgh Mathematical Society 1965

References

REFERENCES

(1) Kilmister, C. W., Proc. Edinburgh Math. Soc. (II), 12 (1961), 13 (Mathematical Note).Google Scholar
(2) Rayner, C. B., C. R. Acad. Sci. Paris, 249 (1959), 1327.Google Scholar