We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 20 January 2009
The sequence of orthogonal functions derived from Laguerre-polynomials is known to be complete, and hence closed, in L2 (0, ∞) if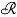 
(a) > − 1. In a recent paper Dr Kober introduced a generalisation of this sequence, which enables him to extend the known results also for 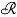(a) < − 1. Kober's guiding principle seems to be the following one: The Laguerre orthogonal functions form, for 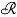(a) > − 1, a complete system of self and skew reciprocal functions of the Hankel transformation of order a. Now, if 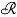(a) < − 1, the ordinary Hankel transform has to be replaced by so-called cut Hankel transform. Hence the system of functions which has to replace-Laguerre orthogonal functions when 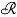(a) < − 1, should be a complete system of self and skew reciprocal functions of the cut Hankel transformation of order a, such that it reduces for 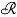(a) > − 1 (when the cut Hankel transform reduces to the ordinary one) to the sequence of Laguerre orthogonal functions. This, of course, is by no means a unique definition; nevertheless, together with what one would call the permanence of the Mellin transform, it enabled Kober to find a sequence of functions 
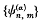which (i) reduces to the sequence of Laguerre orthogonal functions when 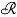(a) > − 1, m = 0, (ii) is a complete set of self and skew reciprocal functions of the cut Hankel transformation with kernel Ja, m and (iii) has the required qualities of completeness and closedness.
page 193 note 1 Kober, Kober.Proc. Edinburgh Math. Soc. (2), 6 (1940), 135–146.CrossRefGoogle Scholar
page 196 note 1 Erdélyi, A., Quart. J. of Math. (Oxford Series) 9 (1938), 196–8 (8).Google Scholar
page 196 note 2 Kober, H.Quart. J. of Math. (Oxford Series) 10 (1939), 45–59CrossRefGoogle Scholar, especially section Kober takes k = ½ (1 + i cot π r), r real and not integral.
page 197 note 1 The cut Hankel transform is mentioned in Titchinarsh's, E. C.Introduction to the theory of Fourier integrals (Oxford, 1937)Google Scholar, § 8.4 Example (1); a full discussion of 
was given by Kober, H.Quart. J. of Math. (Oxford Series) 8 (1937), 186–99.CrossRefGoogle Scholar
page 198 note 1 Quart. J. of Math. (Oxford Series) 11 (1940), 212–21, Theorems 3 and 4.Google Scholar
page 200 note 1 Humbert, P., Proc. Royal Soc, Edinburgh, 41 (1920/1921), 73–96.CrossRefGoogle Scholar See also Appell, P. et Kampé, J., Fonctions hypergéometriques. Polynoines d'Uermite. (Paris, 1926), p. 126.Google Scholar
page 200 note 2 Erdeélyi, A.Wiener Sitzungsberichte, 146 (1937), 431–67 (11, 3).Google Scholar
page 200 note 3 Abschnitt III of the paper quoted in the preceding footnote.Google Scholar
page 202 note 1 Appell et Kampé de Fériet, l.e., p. 14 (11). See also Whittaker, E. T. and Watson, G. N.Modem Analysis (Cambridge, 1927), p. 300, Example 22.Google Scholar
page 208 note 1 Quart. J. of Math. (Oxford Series), 11 (1940), 111–123.Google Scholar
page 209 note 1 Kober, H., Ann. of Math., 40 (1939), 549–59, Satz IV.CrossRefGoogle Scholar
page 211 note 1 DrKober, in a letter, remarks that, of course, a (u2) may be a Laurent series as well. In this case the summation has to run from – α to + α.Google Scholar
page 213 note 1 For the definition of total operators see Banach, S., Théorie des opérations linéaires (Warszawa, 1932), p. 42.Google Scholar
page 213 note 2 Kober, H., Proc. Edinburgh Math. Soc. (2), 6 (1940), 135–146 (3.5).CrossRefGoogle Scholar
page 215 note 1 Watson, G. N., Proc. London Math. Soc. (2), 35 (1933), 156–99.CrossRefGoogle Scholar
page 215 note 2 Busbridge, I. W.Journal London Math. Soc, 9 (1934), 179–87.CrossRefGoogle Scholar
page 215 note 3 Kober, H.Quart. J. of Math. (Oxford Series), 8 (1937), 172–85.CrossRefGoogle Scholar
page 215 note 4 H. Kober Ibidem, 186–99.
page 215 note 5 Tricomi, F., Rend, dei Lincei (6), 22 (1935), 564–71 and 572–6.Google ScholarAtti Torino, 71 (1936), 285–91.Google Scholar
page 215 note 6 Tricomi's method has been used in connection with the operational calculus. van der Pol, B. and Niessen, K. F., Phil. Mag. (7), 13 (1932), 537–75CrossRefGoogle Scholar, eventually established Tricomi's theorem as a “rule” in the particular cases a = 0, 1 before Tricomi dealt with the general case. Niessen, K. F., Phil. Mag. (7), 20 (1935), 977–97, formulated the general rule for a = 0, 1, 2,…… independent from and at the same time as Tricomi. This rule has been frequently used by several authors for evaluation of Hankel transforms.CrossRefGoogle Scholar
page 217 note 1 Cf. also § 9.3 of Titchmarsh's Fourier integrals.Google Scholar
You have
Access
