Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-06-02T20:08:23.127Z Has data issue: false hasContentIssue false
  • English
  • Français

A quantitative version of James's Compactness Theorem

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  23 February 2012

Bernardo Cascales ,
Ondřej F. K. Kalenda  and
Jiří Spurný
Bernardo Cascales
Affiliation:
Departamento de Matemáticas, Universidad de Murcia, 30100 Espinardo, Murcia, Spain (beca@um.es)
Ondřej F. K. Kalenda
Affiliation:
Department of Mathematical Analysis, Faculty of Mathematics and Physics, Charles University, Sokolovská 83, 18675 Praha 8, Czech Republic (kalenda@karlin.mff.cuni.cz; spurny@karlin.mff.cuni.cz)
Jiří Spurný
Affiliation:
Department of Mathematical Analysis, Faculty of Mathematics and Physics, Charles University, Sokolovská 83, 18675 Praha 8, Czech Republic (kalenda@karlin.mff.cuni.cz; spurny@karlin.mff.cuni.cz)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

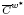We introduce two measures of weak non-compactness JaE and Ja that quantify, via distances, the idea of boundary that lies behind James's Compactness Theorem. These measures tell us, for a bounded subset C of a Banach space E and for given x* ∈ E*, how far from E or C one needs to go to find x** ∈ ⊂ E** with x**(x*) = sup x*(C). A quantitative version of James's Compactness Theorem is proved using JaE and Ja, and in particular it yields the following result. Let C be a closed convex bounded subset of a Banach space E and r > 0. If there is an element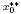in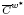whose distance to C is greater than r, then there is x* ∈ E* such that each x** ∈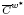at which sup x*(C) is attained has distance to E greater than ½r. We indeed establish that JaE and Ja are equivalent to other measures of weak non-compactness studied in the literature. We also collect particular cases and examples showing when the inequalities between the different measures of weak non-compactness can be equalities and when the inequalities are sharp.

Keywords

Banach spacemeasure of weak non-compactnessJames's Compactness Theorem

MSC classification

Secondary: 46B50: Compactness in Banach (or normed) spaces
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 55 , Issue 2 , June 2012 , pp. 369 - 386
Copyright
Copyright © Edinburgh Mathematical Society 2012

References

1.Angosto, C., Distance to spaces of functions, PhD Thesis, Universidad de Murcia (2007).Google Scholar
2.Angosto, C. and Cascales, B., Measures of weak noncompactness in Banach spaces, Topol. Applic. 156(7) (2009), 1412–1421.CrossRefGoogle Scholar
3.Astala, K. and Tylli, H.-O., Seminorms related to weak compactness and to Tauberian operators, Math. Proc. Camb. Phil. Soc. 107 (1990), 367–375.CrossRefGoogle Scholar
4.Banaś, J. and Martinón, A., Measures of weak noncompactness in Banach sequence spaces, Portugaliae Math. 52 (1995), 131–138.Google Scholar
5.Cascales, B., Marciszewski, W. and Raja, M., Distance to spaces of continuous functions, Topol. Applic. 153 (2006), 2303–2319.CrossRefGoogle Scholar
6.De Blasi, F. S., On a property of the unit sphere in a Banach space, Colloq. Math. 65 (1992), 333–343.Google Scholar
7.Fabian, M., Hájek, P., Montesinos, V. and Zizler, V., A quantitative version of Krein's Theorem, Rev. Mat. Ibero. 21 (2005), 237–248.CrossRefGoogle Scholar
8.Granero, A. S., An extension of the Krein–Šmulian theorem, Rev. Mat. Ibero. 22(1) (2006), 93–110.CrossRefGoogle Scholar
9.Granero, A. S. and Sánchez, M., Convexity, compactness and distances, in Methods in Banach space theory, London Mathematical Society Lecture Note Series, Volume 337, pp. 215–237 (Cambridge University Press, 2006).CrossRefGoogle Scholar
10.Granero, A. S., Hájek, P. and Santalucía, V. Montesinos, Convexity and w *-compactness in Banach spaces, Math. Annalen 328 (2004), 625–631.CrossRefGoogle Scholar
11.James, R. C., Weakly compact sets, Trans. Am. Math. Soc. 113 (1964), 129–140.CrossRefGoogle Scholar
12.Kryczka, A., Quantitative approach to weak noncompactness in the polygon interpolation method, Bull. Austral. Math. Soc. 69 (2004), 49–62.CrossRefGoogle Scholar
13.Kryczka, A., Prus, S., and Szczepanik, M., Measure of weak noncompactness and real interpolation of operators, Bull. Austral. Math. Soc. 62 (2000), 389–401.CrossRefGoogle Scholar
14.Pryce, J. D., Weak compactness in locally convex spaces, Proc. Am. Math. Soc. 17 (1966), 148–155.CrossRefGoogle Scholar