No CrossRef data available.
Published online by Cambridge University Press: 13 June 2016
We define the Schur multipliers of a separable von Neumann algebra 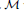 with Cartan maximal abelian self-adjoint algebra
with Cartan maximal abelian self-adjoint algebra 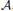 , generalizing the classical Schur multipliers of
, generalizing the classical Schur multipliers of 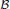 (ℓ 2). We characterize these as the normal
(ℓ 2). We characterize these as the normal 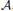 -bimodule maps on
-bimodule maps on 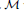 . If
. If 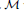 contains a direct summand isomorphic to the hyperfinite II1 factor, then we show that the Schur multipliers arising from the extended Haagerup tensor product
contains a direct summand isomorphic to the hyperfinite II1 factor, then we show that the Schur multipliers arising from the extended Haagerup tensor product 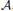 ⊗ eh
⊗ eh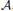 are strictly contained in the algebra of all Schur multipliers.
are strictly contained in the algebra of all Schur multipliers.