Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-05-11T13:46:02.631Z Has data issue: false hasContentIssue false
  • English
  • Français

Some inequalities for a hypergeometric integral

Published online by Cambridge University Press:  20 January 2009

T. M. Flett
T. M. Flett
Affiliation:
Department of Pure Mathematics, The University, Sheffield
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In various problems in harmonic analysis (4, 5, 6), I have required an estimate for the integral for the hypergeometric function

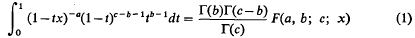
in the case where a>c−b>0, b>0, and 0 ≦ x < 1 (the integral is then unbounded as x→l−). Although there are innumerable identities for hypergeometric functions, few inequalities for these functions seem to be known, and in estimating the integral (1) I employed ad hoc arguments that made no use of the theory of hypergeometric functions. The estimates obtained were adequate for my purposes, but were far from sharp, and the object of this note is to show that, by assembling a few known facts concerning hypergeometric functions, we can obtain sharp inequalities for the integral (1). We also give (in §4) several related inequalities that can be obtained by transforming the integral.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 18 , Issue 1 , June 1972 , pp. 31 - 34
Copyright
Copyright © Edinburgh Mathematical Society 1972

References

REFERENCES

(1) Copson, E. T., An Introduction to the Theory of Functions of a Complex Variable (Oxford, 1935).Google Scholar
(2) Erber, T., Inequalities for hypergeometric functions, Arch. Rational Mech. and Anal. 4 (1959-1960), 341–351.CrossRefGoogle Scholar
(3) Erdèlyi, A. (Ed.), Higher Transcendental Functions, Vol. 1, Bateman Manuscript Project (McGraw-Hill, 1953).Google Scholar
(4) Flett, T. M., Some theorems on fractional integrals, Proc. Cambridge Philos. Soc. 55 (1959), 31–50.CrossRefGoogle Scholar
(5) Flett, T. M., A theorem on functions of class Hλ, Proc. London Math. Soc. (3) 14A (1965), 86–92.CrossRefGoogle Scholar
(6) Flett, T. M., Mean values of power series, Pacific J. Math. 25 (1968), 463–494.CrossRefGoogle Scholar