No CrossRef data available.
Article contents
Unit sphere fibrations in Euclidean space
Published online by Cambridge University Press: 07 March 2024
Abstract
We show that if an open set in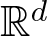 
$\mathbb{R}^d$ can be fibered by unit n-spheres, then 
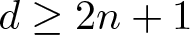$d \geq 2n+1$, and if 
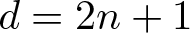$d = 2n+1$, then the spheres must be pairwise linked, and 
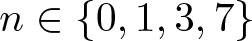$n \in \left\{0, 1, 3, 7 \right\}$. For these values of n, we construct unit n-sphere fibrations in 
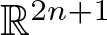$\mathbb{R}^{2n+1}$.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.
References
Bankston, P. and Fox, R., Topological partitions of Euclidean space by spheres, Amer. Math. Monthly 92(6) (1985), 423–424.CrossRefGoogle Scholar
Bankston, P. and McGovern, R., Topological partitions, General Topol. Appl. 10(3) (1979), 215–229.CrossRefGoogle Scholar
Bass, C., Some special decompositions of E 3, Trans. Amer. Math. Soc. 216 (1976), 115–130.Google Scholar
Bing, R. H., Partially continuous decompositions, Proc. Amer. Math. Soc. 6(1) (1955), 124–133.CrossRefGoogle Scholar
Bing, R. H., Some monotone decompositions of a cube, Ann. Math. 61 (1955), 279–288.CrossRefGoogle Scholar
Bing, R. H., A decomposition of E 3 into points and tame arcs such that the decomposition space is topologically different from E 3, Ann. Math. 65 (1957), 484–500.CrossRefGoogle Scholar
Bing, R. H., Upper semicontinuous decompositions of E 3, Ann. Math. 65 (1957), 363–374.CrossRefGoogle Scholar
Bing, R. H. and Curtis, M. L., Imbedding decompositions of E 3 in E 4, Proc. Amer. Math. Soc. 11(1) (1960), 149–155.Google Scholar
Cobb, J., Nice decompositions of 
$\mathbb{R}^n$ entirely into nice sets are mostly impossible, Geom. Dedicata 62(1) (1996), 107–114.CrossRefGoogle Scholar
$\mathbb{R}^n$ entirely into nice sets are mostly impossible, Geom. Dedicata 62(1) (1996), 107–114.CrossRefGoogle ScholarConway, J. H. and Croft, H. T., Covering a sphere with congruent great-circle arcs, Math. Proc. Cambridge Philos. Soc. 60 (1964), 787–800.CrossRefGoogle Scholar
Gluck, H. and Warner, F., Great circle fibrations of the three-sphere, Duke Math. J. 50 (1983), 107–132.CrossRefGoogle Scholar
Gluck, H., Warner, F. and Yang, C., Division algebras, fibrations of spheres by great spheres and the topological determination of a space by the gross behavior of its geodesics, Duke Math. J. 50 (1983), 1041–1076.CrossRefGoogle Scholar
Gluck, H., Warner, F. and Ziller, W., The geometry of the Hopf fibrations, Enseign. Math. (2) 32(3–4) (1986), 173–198.Google Scholar
Harrison, M., Contact structures induced by skew fibrations of $\mathbb{R}^3$, Bull. Lond. Math. Soc. 51 (2019), 887–899.CrossRefGoogle Scholar
$\mathbb{R}^3$, Bull. Lond. Math. Soc. 51 (2019), 887–899.CrossRefGoogle ScholarHarrison, M., Skew and sphere fibrations, Trans. Amer. Math. Soc. 376 (2023), 7107–7137.Google Scholar
Jonsson, M. and Wästlund, J., Partitions of $\mathbb{R}^3$ into curves, Math. Scand. 83 (1998), 192–204.CrossRefGoogle Scholar
$\mathbb{R}^3$ into curves, Math. Scand. 83 (1998), 192–204.CrossRefGoogle ScholarKomjáth, P., Set theoretic constructions in euclidean spaces, New trends in discrete and computational geometry, Algorithms and Combinatorics (ed. Pach, J.), pp. 303–325 (Berlin Heidelberg: Springer, 1993).CrossRefGoogle Scholar
, MathOverflow, Can $\mathbb{R}^3$ be expressed as a disjoint union of pairwise linked circles? Available at: https://mathoverflow.net/questions/173387/can-r3-be-expressed-as-a-disjoint-union-of-pairwise-linked-circles, Accessed: 2022-09-12.Google Scholar
$\mathbb{R}^3$ be expressed as a disjoint union of pairwise linked circles? Available at: https://mathoverflow.net/questions/173387/can-r3-be-expressed-as-a-disjoint-union-of-pairwise-linked-circles, Accessed: 2022-09-12.Google Scholar, MathOverflow, Concerning proofs from the axiom of choice that $\mathbb{R}^3$ admits surprising geometrical decompositions: can we prove there is no borel decomposition? Available at: https://mathoverflow.net/questions/93601/concerning-proofs-from-the-axiom-of-choice-that-R3-admits-surprising-geometrical, Accessed: 2022-09-12.Google Scholar
$\mathbb{R}^3$ admits surprising geometrical decompositions: can we prove there is no borel decomposition? Available at: https://mathoverflow.net/questions/93601/concerning-proofs-from-the-axiom-of-choice-that-R3-admits-surprising-geometrical, Accessed: 2022-09-12.Google Scholar, MathOverflow, Covering the space by disjoint unit circles, Available at: https://mathoverflow.net/questions/162324/covering-the-space-by-disjoint-unit-circles, Accessed: 2022-09-12.Google Scholar
, MathOverflow, Filling $\mathbb{R}^3$ with skew lines, Available at: https://mathoverflow.net/questions/92919/filling-mathbbr3-with-skew-lines, Accessed: 2022-09-12.Google Scholar
$\mathbb{R}^3$ with skew lines, Available at: https://mathoverflow.net/questions/92919/filling-mathbbr3-with-skew-lines, Accessed: 2022-09-12.Google Scholar, MathOverflow, Is it possible to partition $\mathbb{R}^3$ into unit circles? Available at: https://mathoverflow.net/questions/28647/is-it-possible-to-partition-mathbb-r3-into-unit-circles, Accessed: 2022-09-12.Google Scholar
$\mathbb{R}^3$ into unit circles? Available at: https://mathoverflow.net/questions/28647/is-it-possible-to-partition-mathbb-r3-into-unit-circles, Accessed: 2022-09-12.Google ScholarMcKay, B., The Blaschke conjecture and great circle fibrations of spheres, Amer. J. Math. 126 (2004), 1155–1191.CrossRefGoogle Scholar
Moussong, G. and Simányi, N., Circle decompositions of surfaces, Topology Appl. 158(3) (2011), 392–396.CrossRefGoogle Scholar
Ovsienko, V. and Tabachnikov, S., On fibrations with flat fibres, Bull. Lond. Math. Soc. 45 (2013), 625–632.CrossRefGoogle Scholar
Ovsienko, V. and Tabachnikov, S., Hopf fibrations and Hurwitz-Radon numbers, Math. Intelligencer 38(4) (2016), 11–18.CrossRefGoogle Scholar
Szulkin, A., R3 is the union of disjoint circles, Amer. Math. Monthly 90(9) (1983), 640–641.Google Scholar
Vogt, E., A foliation of $\mathbb{R}^3$ and other punctured 3-manifolds by circles, Publ. Math. IHES 69 (1989), 215–232.CrossRefGoogle Scholar
$\mathbb{R}^3$ and other punctured 3-manifolds by circles, Publ. Math. IHES 69 (1989), 215–232.CrossRefGoogle ScholarWilker, J. B., Tiling $\mathbb{R}^3$ with circles and disks, Geom. Dedicata 32(2) (1989), 203–209.CrossRefGoogle Scholar
$\mathbb{R}^3$ with circles and disks, Geom. Dedicata 32(2) (1989), 203–209.CrossRefGoogle Scholar