Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hestroffer, Daniel
Mouret, S.
Mignard, F.
Tanga, P.
and
Berthier, J.
2009.
Gaia and the asteroids: Local test of GR.
Proceedings of the International Astronomical Union,
Vol. 5,
Issue. S261,
p.
325.
Anderson, John D.
and
Nieto, Michael Martin
2009.
Astrometric solar-system anomalies.
Proceedings of the International Astronomical Union,
Vol. 5,
Issue. S261,
p.
189.
Iorio, Lorenzo
2010.
Solar system constraints on planetary Coriolis-type effects induced by rotation of distant masses.
Journal of Cosmology and Astroparticle Physics,
Vol. 2010,
Issue. 08,
p.
030.
Iorio, Lorenzo
2010.
Phenomenological constraints on Lemaître-Tolman-Bondi cosmological inhomogeneities from solar system dynamics.
Journal of Cosmology and Astroparticle Physics,
Vol. 2010,
Issue. 06,
p.
004.
Fienga, A.
Laskar, J.
Kuchynka, P.
Manche, H.
Desvignes, G.
Gastineau, M.
Cognard, I.
and
Theureau, G.
2011.
The INPOP10a planetary ephemeris and its applications in fundamental physics.
Celestial Mechanics and Dynamical Astronomy,
Vol. 111,
Issue. 3,
p.
363.
Gai, Mario
Vecchiato, Alberto
Ligori, Sebastiano
Sozzetti, Alessandro
and
Lattanzi, Mario G.
2012.
Gravitation astrometric measurement experiment.
Experimental Astronomy,
Vol. 34,
Issue. 2,
p.
165.
Křížek, Michal
2012.
Dark energy and the anthropic principle.
New Astronomy,
Vol. 17,
Issue. 1,
p.
1.
Pitjeva, E. V.
and
Pitjev, N. P.
2012.
Changes in the Sun’s mass and gravitational constant estimated using modern observations of planets and spacecraft.
Solar System Research,
Vol. 46,
Issue. 1,
p.
78.
Avalos-Vargas, A.
and
Ares de Parga, G.
2012.
The precession of the orbit of a charged body interacting with a massive charged body in General Relativity.
The European Physical Journal Plus,
Vol. 127,
Issue. 12,
Kuchynka, Petr
and
Folkner, William M.
2013.
A new approach to determining asteroid masses from planetary range measurements.
Icarus,
Vol. 222,
Issue. 1,
p.
243.
Pitjeva, E. V.
and
Pitjev, N. P.
2014.
Development of planetary ephemerides EPM and their applications.
Celestial Mechanics and Dynamical Astronomy,
Vol. 119,
Issue. 3-4,
p.
237.
Fienga, A.
Laskar, J.
Exertier, P.
Manche, H.
and
Gastineau, M.
2015.
Numerical estimation of the sensitivity of INPOP planetary ephemerides to general relativity parameters.
Celestial Mechanics and Dynamical Astronomy,
Vol. 123,
Issue. 3,
p.
325.
Lucchesi, D M
Anselmo, L
Bassan, M
Pardini, C
Peron, R
Pucacco, G
and
Visco, M
2015.
Testing the gravitational interaction in the field of the Earth via satellite laser ranging and the Laser Ranged Satellites Experiment (LARASE).
Classical and Quantum Gravity,
Vol. 32,
Issue. 15,
p.
155012.
Nyambuya, G.G.
2017.
Apsidal precession of the outer solar planetary orbits due to the pioneer anomaly.
New Astronomy,
Vol. 57,
Issue. ,
p.
22.
Hees, Aurélien
Bourgoin, Adrien
Delva, Pacome
Le Poncin-Lafitte, Christophe
and
Wolf, Peter
2019.
Relativistic Geodesy.
Vol. 196,
Issue. ,
p.
317.
Ye, Hanlin
Zheng, Wei
Guo, Huadong
and
Liu, Guang
2020.
Effects of Temporal Sampling Interval on the Moon-Based Earth Observation Geometry.
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,
Vol. 13,
Issue. ,
p.
4016.
Dudziński, G
Podlewska-Gaca, E
Bartczak, P
Benseguane, S
Ferrais, M
Jorda, L
Hanuš, J
Vernazza, P
Rambaux, N
Carry, B
Marchis, F
Marsset, M
Viikinkoski, M
Brož, M
Fetick, R
Drouard, A
Fusco, T
Birlan, M
Jehin, E
Berthier, J
Castillo-Rogez, J
Cipriani, F
Colas, F
Dumas, C
Kryszczynska, A
Lamy, P
Le Coroller, H
Marciniak, A
Michalowski, T
Michel, P
Santana-Ros, T
Tanga, P
Vachier, F
Vigan, A
Witasse, O
and
Yang, B
2020.
Volume uncertainty of (7) Iris shape models from disc-resolved images.
Monthly Notices of the Royal Astronomical Society,
Vol. 499,
Issue. 3,
p.
4545.
Fienga, A
Avdellidou, C
and
Hanuš, J
2020.
Asteroid masses obtained with INPOP planetary ephemerides.
Monthly Notices of the Royal Astronomical Society,
Vol. 492,
Issue. 1,
p.
589.
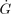 /G = (−5.9±4.4) ⋅ 10−14 per year, the statistic zero corrections to the planet perihelion advances.
/G = (−5.9±4.4) ⋅ 10−14 per year, the statistic zero corrections to the planet perihelion advances.