Published online by Cambridge University Press: 14 November 2011
Let us consider equations in the form
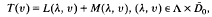
where Λ is an open subset of a normed space. For any fixed λ ∊ Λ, T, L(λ,.) and M(λ,.) are mappings from the closure D0 of a neighbourhood D0 of the origin in a Banach space X into another Banach space Y with T(0) = L(λ, 0) = M(λ, 0) = 0. Let λ be a characteristic value of the pair (T, L) such that T − L(λ,.) is a Fredholm mapping with nullity p and index s, p> s≧ 0. Under sufficient hypotheses on T, L and M, (λ, 0) is a bifurcation point of the above equations. Some well-known results obtained by Crandall and Rabinowitz [2], McLeod and Sattinger [5] and others will be generalised. The results in this paper are extensions of the results obtained by the author in [7].