Hostname: page-component-7dd5485656-frp75 Total loading time: 0 Render date: 2025-10-30T10:18:28.165Z Has data issue: false hasContentIssue false
  • English
  • Français

Schatten class composition operators on the Hardy space

Part of: Holomorphic functions of several complex variables Special classes of linear operators Spaces and algebras of analytic functions

Published online by Cambridge University Press:  24 July 2023

Wenwan Yang  and
Cheng Yuan
Wenwan Yang
Affiliation:
School of Mathematics and Statistics, Guangdong University of Technology, Guangzhou, Guangdong 510520, China (wenwan_yang@163.com, yuancheng1984@163.com)
Cheng Yuan
Affiliation:
School of Mathematics and Statistics, Guangdong University of Technology, Guangzhou, Guangdong 510520, China (wenwan_yang@163.com, yuancheng1984@163.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose $2< p<\infty$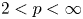 and $\varphi$ 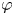is a holomorphic self-map of the open unit disk $\mathbb {D}$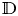. We show the following assertions:

  1. (1) If $\varphi$ 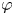has bounded valence and0.1

    \begin{equation} \int_{\mathbb{D}} \left(\frac{1-|z|^2}{1-|\varphi(z)|^2}\right)^{p/2}\frac{\mathrm{d} A(z)}{(1-|z|^2)^2}<\infty, \end{equation}
    then $C_{\varphi }$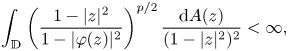 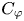is in the Schatten $p$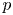-class of the Hardy space $H^2$.

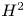  2. (2) There exists a holomorphic self-map $\varphi$ 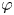(which is, of course, not of bounded valence) such that the inequality (0.1) holds and $C_{\varphi }: H^2\to H^2$ 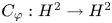does not belong to the Schatten $p$-class.

Keywords

composition operatorsHardy spacesSchatten p-class

MSC classification

Primary: 30H10: Hardy spaces
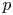Secondary: 32A35: $H^p$-spaces, Nevanlinna spaces 47B10: Operators belonging to operator ideals (nuclear, $p$-summing, in the Schatten-von Neumann classes, etc.) 47B33: Composition operators

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 154 , Issue 5 , October 2024 , pp. 1364 - 1377
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Benazzouz, H., El-Fallah, O., Kellay, K. and Mahzouli, H.. Contact points and Schatten composition operators. Math. Z. 279 (2015), 407–422.CrossRefGoogle Scholar
Bendaoud, Z., Korrichi, F., Merghni, L. and Yagoub, A.. Contact points and Schatten class of composition operators. Indian J. Pure Appl. Math. 49 (2018), 651–661.CrossRefGoogle Scholar
Cowen, C. C. and MacCluer, B. D.. Composition Operators on Spaces of Analytic Functions. Studies in Advanced Mathematics (CRC Press, Boca Raton, FL, 1995).Google Scholar
Luecking, D. H.. Trace ideal criteria for Toeplitz operators. J. Funct. Anal. 73 (1987), 345–368.CrossRefGoogle Scholar
Luecking, D. and Zhu, K.. Composition operators belonging to the Scatten ideals. Amer. J. Math. 114 (1992), 1127–1145.CrossRefGoogle Scholar
Pau, J. and Perälä, A.. A Toeplitz-type operator on Hardy spaces in the unit ball. Trans. Amer. Math. Soc. 373 (2020), 3031–3062.CrossRefGoogle Scholar
Pau, J. and Pérez, P.. Composition operators acting on weighted Dirichlet spaces. J. Math. Anal. Appl. 401 (2013), 682–694.CrossRefGoogle Scholar
Shapiro, J. H.. Composition Operators and Classical Function Theory. Springer (New York, 1993).CrossRefGoogle Scholar
Wirths, K.-J. and Xiao, J.. Global integral criteria for composition operators. J. Math. Anal. Appl. 269 (2002), 702–715.CrossRefGoogle Scholar
Xia, J.. On a proposed characterization of Schatten-class composition operators. Proc. Amer. Math. Soc. 131 (2003), 2505–2514.CrossRefGoogle Scholar
Yang, W. and Liu, J.. Schatten classes of Toeplitz operators on Bergman-Besov Hilbert spaces in the unit ball. J. Math. Anal. Appl. 526 (2023), 127257.CrossRefGoogle Scholar
Yuan, C. and Zhou, Z.. Composition operators belonging to the Schatten class $\mathcal {S}_p$. Bull. Aust. Math. Soc. 81 (2010), 465–472.CrossRefGoogle Scholar
Yuan, C. and Zhou, Z.. The Hilbert-Schmidt norm of a composition operator on the Bergman space. Bull. Aust. Math. Soc. 95 (2017), 250–259.CrossRefGoogle Scholar
Zhu, K.. Schatten class composition operators on weighted Bergman spaces of the disk. J. Operator Theory 46 (2001), 173–181.Google Scholar
Zhu, K.. Translating certain inequalities between Hardy and Bergman spaces. Amer. Math. Monthly 111 (2004), 520–525.CrossRefGoogle Scholar
Zhu, K.. Operator Theory in Function Spaces (American Mathematical Society, Providence, RI, 2007).CrossRefGoogle Scholar