Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gmeineder, Franz
and
Kristensen, Jan
2019.
Sobolev regularity for convex functionals on BD.
Calculus of Variations and Partial Differential Equations,
Vol. 58,
Issue. 2,
Chambolle, Antonin
Conti, Sergio
and
Iurlano, Flaviana
2019.
Approximation of functions with small jump sets and existence of strong minimizers of Griffith's energy.
Journal de Mathématiques Pures et Appliquées,
Vol. 128,
Issue. ,
p.
119.
Conti, Sergio
Focardi, Matteo
and
Iurlano, Flaviana
2019.
Existence of strong minimizers for the Griffith static fracture model in dimension two.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 36,
Issue. 2,
p.
455.
Crismale, Vito
2019.
On the Approximation of SBD Functions and Some Applications.
SIAM Journal on Mathematical Analysis,
Vol. 51,
Issue. 6,
p.
5011.
De Philippis, Guido
and
Rindler, Filip
2020.
Fine properties of functions of bounded deformation-an approach via linear PDEs.
Mathematics in Engineering,
Vol. 2,
Issue. 3,
p.
386.
Friedrich, Manuel
and
Solombrino, Francesco
2020.
Functionals Defined on Piecewise Rigid Functions: Integral Representation and $$\varGamma $$-Convergence.
Archive for Rational Mechanics and Analysis,
Vol. 236,
Issue. 3,
p.
1325.
Caroccia, M.
Focardi, M.
and
Goethem, N. Van
2020.
On the Integral Representation of Variational Functionals on $BD$.
SIAM Journal on Mathematical Analysis,
Vol. 52,
Issue. 4,
p.
4022.
Friedrich, Manuel
2020.
Griffith energies as small strain limit of nonlinear models for nonsimple brittle materials.
Mathematics in Engineering,
Vol. 2,
Issue. 1,
p.
75.
Crismale, Vito
and
Friedrich, Manuel
2020.
Equilibrium Configurations for Epitaxially Strained Films and Material Voids in Three-Dimensional Linear Elasticity.
Archive for Rational Mechanics and Analysis,
Vol. 237,
Issue. 2,
p.
1041.
Friedrich, Manuel
Perugini, Matteo
and
Solombrino, Francesco
2021.
Lower semicontinuity for functionals defined on piecewise rigid functions and on GSBD.
Journal of Functional Analysis,
Vol. 280,
Issue. 7,
p.
108929.
Lipton, Robert P.
and
Jha, Prashant K.
2021.
Nonlocal elastodynamics and fracture.
Nonlinear Differential Equations and Applications NoDEA,
Vol. 28,
Issue. 3,
Benvenuti, Elena
and
Orlando, Nicola
2021.
A mesh-independent framework for crack tracking in elastodamaging materials through the regularized extended finite element method.
Computational Mechanics,
Vol. 68,
Issue. 1,
p.
25.
Cagnetti, Filippo
Chambolle, Antonin
and
Scardia, Lucia
2022.
Korn and Poincaré-Korn inequalities for functions with a small jump set.
Mathematische Annalen,
Vol. 383,
Issue. 3-4,
p.
1179.
Crismale, Vito
Friedrich, Manuel
and
Solombrino, Francesco
2022.
Integral representation for energies in linear elasticity with surface discontinuities.
Advances in Calculus of Variations,
Vol. 15,
Issue. 4,
p.
705.
Almi, Stefano
Davoli, Elisa
and
Friedrich, Manuel
2023.
Non-interpenetration conditions in the passage from nonlinear to linearized Griffith fracture.
Journal de Mathématiques Pures et Appliquées,
Vol. 175,
Issue. ,
p.
1.
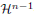 -almost everywhere away from the jump set. On the negative side, we construct a function that is BD but not in BV and has distributional strain consisting only of a jump part, and one that has a distributional strain consisting of only a Cantor part.
-almost everywhere away from the jump set. On the negative side, we construct a function that is BD but not in BV and has distributional strain consisting only of a jump part, and one that has a distributional strain consisting of only a Cantor part.
