Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Peñafort Sanchis, Guillermo
and
Tari, Farid
2024.
On k-folding map-germs and hidden symmetries of surfaces in the Euclidean 3-space.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 154,
Issue. 1,
p.
60.

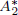 points’, which are not detected by the flat geometry of the surface. These
points’, which are not detected by the flat geometry of the surface. These 