No CrossRef data available.
Article contents
The boundary value problem for triholomorphic maps
Part of:
Global differential geometry
General first-order equations and systems
Variational problems in infinite-dimensional spaces
Published online by Cambridge University Press: 20 November 2025
Abstract
We introduce a natural boundary value problem for a triholomorphic map 
$u$ from a compact almost hyper-Hermitian manifold 
$M$ with smooth boundary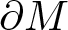 
$\partial M$ into a closed hyperKähler manifold 
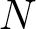$N$ with free boundary 
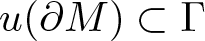$u(\partial M)\subset \Gamma$ lying on some geometrically natural closed supporting submanifold 
$\Gamma\subset N$, called tri-isotropic submanifold. We establish partial regularity theory and energy quantization result in this boundary setting under some additional assumption on the 
$W^{2,1}$ norm of the weakly converging sequences.
Keywords
MSC classification
Primary:
58E20: Harmonic maps , etc.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
Anselmi, D. and Fré, P.. Topological 
$\unicode{x03C3}$-models in four dimensions and triholomorphic maps. Nuclear Phys. B. 416 (1994), 255–300.CrossRefGoogle Scholar
$\unicode{x03C3}$-models in four dimensions and triholomorphic maps. Nuclear Phys. B. 416 (1994), 255–300.CrossRefGoogle ScholarBellettini, C. and Tian, G.. Compactness results for triholomorphic maps. J. Eur. Math. Soc. (JEMS). 21 (2019), 1271–1317.CrossRefGoogle Scholar
Bethuel, F.. On the singular set of stationary harmonic maps. Manuscr. Math. 78 (1993), 417–443.CrossRefGoogle Scholar
Caniato, R. and Rivière, T.. The unique tangent cone property for weakly holomorphic maps into projective algebraic varieties. Duke Math. J. 172 (2023), 2471–2536.CrossRefGoogle Scholar
Charles, B., Morrey, Jr. Multiple integrals in the calculus of variations. Die Grundlehren der Mathematischen Wissenschaften., Vol.130, pp. xii+506 (Springer-Verlag, 1966).Google Scholar
Chen, J. -Y.. Complex anti-self-dual connections on a product of Calabi-Yau surfaces and triholomorphic curves. Comm. Math. Phys. 201 (1999), 217–247.CrossRefGoogle Scholar
Chen, J. -Y. and Jia-Yu, L.. Quaternionic maps between hyperKähler manifolds. J. Diff. Geom. 55 (2000), 355–384.Google Scholar
De-Liang, X.. Liouville type theorems of harmonic maps with free boundary. Acta Math. Sinica. (Chinese Ser.). 47 (2004), 19–26.Google Scholar
Ding, W. -Y. and Tian, G.. Energy identity for a class of approximate harmonic maps from surfaces. Commun. Anal. Geom. 3 (1995), 543–554.CrossRefGoogle Scholar
Donaldson, S. K. and Thomas, P. R.. Gauge theory in higher dimensions. In: The Geometric Universe, pp. 31–47 (Oxford University Press, Oxford, 1998).CrossRefGoogle Scholar
Frè, P. G., Grassi, P. A. and Sorin, A. S.. Hyperinstantons, the Beltrami equation, and triholomorphic maps. Fortschr. Phys. 64 (2016), 151–175.CrossRefGoogle Scholar
Giaquinta, M.. Multiple Integrals in the Calculus of Variations and Nonlinear Elliptic systems. (Princeton Univ. Press, Princeton, NJ, 1983).Google Scholar
Gulliver, R. and Jost, J.. Harmonic maps which solve a free-boundary problem. J. Reine Angew. Math. 381 (1987), 61–89.Google Scholar
Hélein, F.. Harmonic maps, Conservation Laws and Moving frames. (Cambridge University Press, 2002) No. 150.CrossRefGoogle Scholar
Jin, Z. -R.. Liouville theorems for harmonic maps. Invent. Math. 108 (1992), 1–10.CrossRefGoogle Scholar
Jost, J., Liu, L. and Zhu, M.. The qualitative behavior at the free boundary for approximate harmonic maps from surfaces. Math. Ann. 374 (2019), 133–177.CrossRefGoogle ScholarPubMed
Lin, F. -H.. Gradient estimates and blow-up analysis for stationary harmonic maps. Ann. Math. 149 (1999), 785–829.CrossRefGoogle Scholar
Lin, F. -H. and Rivière, T.. Energy quantization for harmonic maps. Duke Math. J. 111 (2002), 177–193.CrossRefGoogle Scholar
Miguel Figueroa-O’Farrill, J., Köhl, C. and Spence, B.. Supersymmetric Yang-Mills, octonionic instantons and triholomorphic curves. Nuclear Phys. B. 521 (1998), 419–443.CrossRefGoogle Scholar
Nigel, J. H.. The self-duality equations on a Riemann surface. Proc. London Math. Soc. 55 (1987), 59–126.Google Scholar
Richard, M. S.. Analytic aspects of the harmonic map problem. Seminar on Nonlinear Partial Differential Εquations 2. pp. 321–358, (Mathematical Sciences Research Institute Publications, Springer, New York, 1984).Google Scholar
Rivière, T.. Interpolation spaces and energy quantization for Yang-Mills fields. Comm. Anal. Geom. 10 (2002), 683–708.CrossRefGoogle Scholar
Rivière, T. and Tian, G.. The singular set of J-holomorphic maps into projective algebraic varieties. J. Reine Angew. Math. 570 (2004), 47–87.Google Scholar
Scheven, C.. (2004) Zur Regularitätstheorie stationärer harmonischer Abbildungen mit freier Randbedingung. Heinrich-Heine-Universität Düsseldorf, Mathematisch-Naturwissenschaftliche Fakultät download under, http://diss.ub.uni-duesseldorf.de/ebib/diss/show?dissid=886.Google Scholar
Scheven, C.. Partial regularity for stationary harmonic maps at a free boundary. Math. Z. 253 (2006), 135–157.CrossRefGoogle Scholar
Schoen, R. M. and Uhlenbeck, K. K.. A regularity theory for harmonic maps. J. Diff. Geom. 17 (1982), 307–335.Google Scholar
Tian, G.. Some regularity problems of stationary harmonic maps. In: Noncompact Problems at the Intersection of Geometry, Analysis, and Topology. Contemp Math., Vol. 350, Amer. Math. Soc (2004), 245–252.CrossRefGoogle Scholar
Wang, C. -Y.. Energy quantization for triholomorphic maps. Calc. Var. Partial Differential Equations. 18 (2003), 145–158.CrossRefGoogle Scholar
William, K. A.. An integrality theorem and a regularity theorem for surfaces whose first variation with respect to a parametric elliptic integrand is controlled. Proc. Symp. Pure Math. 44 (1986), 1–28.Google Scholar