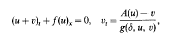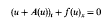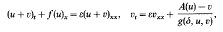Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Klingenberg, Christian
and
Lu, Yun-Guang
1999.
Hyperbolic Problems: Theory, Numerics, Applications.
p.
553.
Dafermos, Constantine M.
2000.
Hyperbolic Conservation Laws in Continuum Physics.
Vol. 325,
Issue. ,
p.
371.
Lu, Yun-Guang
2002.
Singular Limits of Stiff Relaxation and Dominant Diffusion for Nonlinear Systems.
Journal of Differential Equations,
Vol. 179,
Issue. 2,
p.
687.
Gosse, Laurent
2003.
Time-Splitting Schemes and Measure Source Terms for a Quasilinear Relaxing System.
Mathematical Models and Methods in Applied Sciences,
Vol. 13,
Issue. 08,
p.
1081.
Lu, Yun-guang
and
Klingenberg, Christian
2003.
A mixed type system of three equations modelling reacting flows.
Proceedings of the American Mathematical Society,
Vol. 131,
Issue. 11,
p.
3511.
2005.
Hyberbolic Conservation Laws in Continuum Physics.
Vol. 325,
Issue. ,
p.
511.
Scott, James M.
Laiu, M. Paul
and
Hauck, Cory D.
2019.
Analysis of the Zero Relaxation Limit of Hyperbolic Balance Laws with Random Initial Data.
SIAM/ASA Journal on Uncertainty Quantification,
Vol. 7,
Issue. 3,
p.
806.