Article contents
Differential Operators of infinite order
Published online by Cambridge University Press: 14 November 2011
Synopsis
The differential operators in question are of the form G(DZ) where G(w)is an entire function of order at most 1/n and minimal type while Dz is a linear differential operator of order n with coefficients which are entire ( = integral) functions of z, usually polynomials. This class of operators form a natural generalization of the class G(d/dz) studied during the first half of the century Muggli, Polya, Ritt and others. The class G(DZ) was introduced by the present author and his pupils in the 1940s. In fact, the present paper is partly based on a MS from that period, mostly devoted to the special case
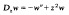
but also containing generalizations, some of which were later worked out by Klimczak. A basic tool in this paper is the characteristic series
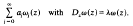
Examples are given showing that the domain of absolute convergence of such a series need neither be convex nor of finite connectivity, a question which has puzzled the author for forty odd years. Characteristic series arising from regular or singular boundary value problems for the operator Dz are used to study the inversion problem
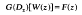
for given F(z). In particular it is shown that exp (Dx)[W(z)] = 0 has the unique solution W(z) ≡ 0. Some singular boundary value problems are considered briefly.
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 86 , Issue 1-2 , 1980 , pp. 85 - 101
- Copyright
- Copyright © Royal Society of Edinburgh 1980
References
- 1
- Cited by

