Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Levine, Howard A.
1990.
The Role of Critical Exponents in Blowup Theorems.
SIAM Review,
Vol. 32,
Issue. 2,
p.
262.
Lindblad, Hans
1990.
Blow-up for solutions of □u=|u|pwith small initial data..
Communications in Partial Differential Equations,
Vol. 15,
Issue. 6,
p.
757.
Pecher, Hartmut
1990.
Global smooth solutions to a class of semilinear wave equaiions with strong nonlinearities.
Manuscripta Mathematica,
Vol. 69,
Issue. 1,
p.
71.
Kimitoshi, Tsutaya
and
Agemi, R.
1992.
A Global Existence Theorem for Semilinear Wave Equations with Data of Non Compact Support in Two Space Dimensions.
Communications in Partial Differential Equations,
Vol. 17,
Issue. 11-12,
p.
1925.
Tsutaya, Kimitoshi
1992.
Scattering theory for semilinear wave equations with small data in two space dimensions.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 68,
Issue. 8,
Takamura, Hiroyuki
1994.
An elementary proof of the exponential blow‐up for semi‐linear wave equations.
Mathematical Methods in the Applied Sciences,
Vol. 17,
Issue. 4,
p.
239.
Tsutaya, Kimitoshi
1994.
Scattering theory for semilinear wave equations with small data in two space dimensions.
Transactions of the American Mathematical Society,
Vol. 342,
Issue. 2,
p.
595.
Liu, Yue
1995.
Instability and Blow-Up of Solutions to a Generalized Boussinesq Equation.
SIAM Journal on Mathematical Analysis,
Vol. 26,
Issue. 6,
p.
1527.
Lindblad, Hans
and
Sogge, Christopher D.
1996.
Partial Differential Equations and Mathematical Physics.
p.
211.
Deng, Keng
1997.
Nonexistence of global solutions of a nonlinear hyperbolic system.
Transactions of the American Mathematical Society,
Vol. 349,
Issue. 4,
p.
1685.
KUBO, Hideo
and
KUBOTA, Kôji
1998.
Asymptotic behaviors of radially symmetric solutions of _??_<i>u</i>=|<i>u</i>|<sup><i>p</i></sup> for super critical values <i>p</i> in even space dimensions.
Japanese journal of mathematics. New series,
Vol. 24,
Issue. 2,
p.
191.
Belchev, Eugene
Kepka, Mariusz
and
Zhou, Zhengfang
1999.
Global Existence of Solutions to Nonlinear Wave Equations.
Communications in Partial Differential Equations,
Vol. 24,
Issue. 11-12,
p.
110.
Kubo, Hideo
and
Ohta, Masahito
1999.
Critical Blowup for Systems of Semilinear Wave Equations in Low Space Dimensions.
Journal of Mathematical Analysis and Applications,
Vol. 240,
Issue. 2,
p.
340.
Deng, Keng
1999.
Blow-Up of Solutions of Some Nonlinear Hyperbolic Systems.
Rocky Mountain Journal of Mathematics,
Vol. 29,
Issue. 3,
Agemi, Rentaro
Kurokawa, Yuki
and
Takamura, Hiroyuki
2000.
Critical Curve for p-q Systems of Nonlinear Wave Equations in Three Space Dimensions.
Journal of Differential Equations,
Vol. 167,
Issue. 1,
p.
87.
Lai, Shaoyong
2000.
THE GLOBAL AND LOCAL C 2 -SOLUTIONS FOR THE WAVE EQUATION□u=G(ut, Du)IN THREE SPACE DIMENSIONS.
Acta Mathematica Scientia,
Vol. 20,
Issue. 4,
p.
495.
Kubo, Hideo
and
Ohta, Masahito
2000.
Small Data Blowup for Systems of Semilinear Wave Equations with Different Propagation Speeds in Three Space Dimensions.
Journal of Differential Equations,
Vol. 163,
Issue. 2,
p.
475.
D'Ancona, Piero
Georgiev, Vladimir
and
Kubo, Hideo
2001.
Weighted Decay Estimates for the Wave Equation.
Journal of Differential Equations,
Vol. 177,
Issue. 1,
p.
146.
Zhang, Ping
and
Zheng, Yuxi
2001.
RAREFACTIVE SOLUTIONS TO A NONLINEAR VARIATIONAL WAVE EQUATION OF LIQUID CRYSTALS.
Communications in Partial Differential Equations,
Vol. 26,
Issue. 3-4,
p.
381.
Belchev, Eugene
Kepka, Mariusz
and
Zhou, Zhengfang
2002.
Finite-Time Blow-Up of Solutions to Semilinear Wave Equations.
Journal of Functional Analysis,
Vol. 190,
Issue. 1,
p.
233.

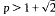 but that small data solutions blow up in finite time if
but that small data solutions blow up in finite time if 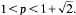 Glassey has shown the two dimensional case is similar. This paper shows that small data solutions blow up in finite time when
Glassey has shown the two dimensional case is similar. This paper shows that small data solutions blow up in finite time when 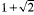 in three dimensions and
in three dimensions and 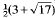 in two.
in two.