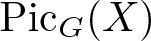1. Introduction
In this paper, we take the approach of functor of points to study equivariant vector bundles on schemes over semirings and monoids. The functor of points approach of schemes says that one may view schemes as locally representable sheaves on the category of commutative rings. In fact, Töen and Vaquié [Reference Perling and Schröer28] developed scheme theory over a closed symmetric monoidal category ![]() $\mathcal{C}$ by defining schemes as (suitably defined) locally representable sheaves on
$\mathcal{C}$ by defining schemes as (suitably defined) locally representable sheaves on ![]() $\mathcal{C}$. The construction is entirely formal and category-theoretic, and hence one may immediately apply the construction of Töen and Vaquié to various closed symmetric monoidal categories
$\mathcal{C}$. The construction is entirely formal and category-theoretic, and hence one may immediately apply the construction of Töen and Vaquié to various closed symmetric monoidal categories ![]() $\mathcal{C}$ to have scheme theory over
$\mathcal{C}$ to have scheme theory over ![]() $\mathcal{C}$ without much effort. For instance, when
$\mathcal{C}$ without much effort. For instance, when ![]() $\mathcal{C}$ is the category of
$\mathcal{C}$ is the category of ![]() $\mathbb{N}$-algebras (i.e., semirings), the theory of Töen and Vaquié immediately gives us schemes over
$\mathbb{N}$-algebras (i.e., semirings), the theory of Töen and Vaquié immediately gives us schemes over ![]() $\mathbb{N}$, as it does for schemes over
$\mathbb{N}$, as it does for schemes over ![]() $\mathbb{Z}$. Likewise, Töen and Vaquié’s theory applied to the category of (pointed) monoids gives one monoid schemes, which is equivalent to monoid schemes constructed via prime ideals first introduced by Deitmar [Reference Deitmar10] (See [Reference Marty25] for the equivalence between [Reference Perling and Schröer28] and [Reference Deitmar10] for monoid schemes).
$\mathbb{Z}$. Likewise, Töen and Vaquié’s theory applied to the category of (pointed) monoids gives one monoid schemes, which is equivalent to monoid schemes constructed via prime ideals first introduced by Deitmar [Reference Deitmar10] (See [Reference Marty25] for the equivalence between [Reference Perling and Schröer28] and [Reference Deitmar10] for monoid schemes).
While the theory proposed by Töen and Vaquié [Reference Perling and Schröer28] is intriguing, it offers an opportunity for further enrichment through the incorporation of concrete examples. In this regard, the exploration of monoids and semirings presents an ideal place for not only testing but also enhancing the applicability and clarity of this theory.
We will take this approach in the special case of the category of monoids and semirings in order to study vector bundles. Scheme theory over monoids is very closely related to toric varieties. For instance, in [Reference Cortiñas, Haesemeyer, Walker and Weibel8], Cortiñas, Haesemeyer, Walker, and Weibel utilized the theory of monoid schemes to study the algebraic K-theory of blow-up squares of toric varieties and schemes. Semirings naturally appear in various areas of mathematics; however in this paper, our focus will be on algebraic geometry over semirings.
To develop scheme theory over semirings, one may consider two types of semirings based on their relations to rings.
Firstly, there are semirings which are subsets of rings, such as ![]() $\mathbb{N}$ or
$\mathbb{N}$ or ![]() $\mathbb{R}_{ \gt 0}$. One potential application of developing scheme theory over these semirings would be to obtain positive models for schemes over rings. This can be seen as an analogy to the fact that schemes over
$\mathbb{R}_{ \gt 0}$. One potential application of developing scheme theory over these semirings would be to obtain positive models for schemes over rings. This can be seen as an analogy to the fact that schemes over ![]() $\mathbb{Z}$ provide integral models of schemes over
$\mathbb{Z}$ provide integral models of schemes over ![]() $\mathbb{Q}$. For instance, in [Reference Borger and Jun6], Borger and the first author show that the narrow class group of a number field can be recovered as a reflexive Picard group of its subsemiring of totally nonnegative algebraic integers (See the introduction of [Reference Borger and Jun6] for more detailed explanation concerning positive models of schemes). Similarly, one can develop a theory of algebraic groups over semifields to capture positivity, such as in [Reference Bao and Xuhua3] and [Reference Lusztig24].
$\mathbb{Q}$. For instance, in [Reference Borger and Jun6], Borger and the first author show that the narrow class group of a number field can be recovered as a reflexive Picard group of its subsemiring of totally nonnegative algebraic integers (See the introduction of [Reference Borger and Jun6] for more detailed explanation concerning positive models of schemes). Similarly, one can develop a theory of algebraic groups over semifields to capture positivity, such as in [Reference Bao and Xuhua3] and [Reference Lusztig24].
The second type is (additively) idempotent semirings, which can never be embedded in rings. A class of such semirings arises naturally from totally ordered abelian groups G as follows: let ![]() $S=G\cup \{-\infty\}$. The multiplication of S is the addition of G and the addition of S is defined by
$S=G\cup \{-\infty\}$. The multiplication of S is the addition of G and the addition of S is defined by ![]() $a+b = \max\{a,b\}$ with
$a+b = \max\{a,b\}$ with ![]() $-\infty$ the smallest element. When
$-\infty$ the smallest element. When ![]() $G=\mathbb{R}$, the associated semiring is called the tropical semifield denoted by
$G=\mathbb{R}$, the associated semiring is called the tropical semifield denoted by ![]() $\mathbb{T}$.
$\mathbb{T}$.
Tropical geometry is a version of algebraic geometry over the tropical semifield (or its variants, described for instance in [Reference Lorscheid23]). Tropical geometry brings a new set of combinatorial tools to approach classical problems in algebraic geometry.
Although the two types of semirings and semiring geometries described above may seem intrinsically different, they complement each other. In algebraic geometry, we often study a scheme X over ![]() $\mathbb{Z}$ through its base changes to
$\mathbb{Z}$ through its base changes to ![]() $X_{{\mathbb{F}}_q}$ or
$X_{{\mathbb{F}}_q}$ or ![]() $X_{\mathbb{C}}$. Similarly here, one may consider a scheme X over
$X_{\mathbb{C}}$. Similarly here, one may consider a scheme X over ![]() $\mathbb{N}$ and its base change to
$\mathbb{N}$ and its base change to ![]() $\mathbb{T}$, which we denote by
$\mathbb{T}$, which we denote by ![]() $X_{\mathbb{T}}$. In some sense, for a scheme X over
$X_{\mathbb{T}}$. In some sense, for a scheme X over ![]() $\mathbb{N}$, the ‘complement’ of
$\mathbb{N}$, the ‘complement’ of ![]() $X_{\mathbb{T}}$ is
$X_{\mathbb{T}}$ is ![]() $X_{\mathbb{Z}}$ as a semiring R is a ring if and only if
$X_{\mathbb{Z}}$ as a semiring R is a ring if and only if ![]() $R\otimes_{\mathbb{N}}\mathbb{T}=\{0\}$. See [Reference Borger4] and [Reference Borger and Grinberg5].
$R\otimes_{\mathbb{N}}\mathbb{T}=\{0\}$. See [Reference Borger4] and [Reference Borger and Grinberg5].
In this paper we focus our attention to schemes over additively idempotent semifields. We explore several properties of equivariant vector bundles on schemes over idempotent semifields, especially torus-equivariant vector bundles on the toric scheme XR associated with a fan, where R is a semiring. Loosely speaking, XR is a semiring scheme over R obtained from the monoid scheme associated with a fan via a base change to R. For a rigorous definition and examples we refer the reader to §2.
Recently, there has been a lot of interest in extending tropical methods to the study of vector bundles and thus developing the notion of tropical vector bundles. The proposed definitions of tropical vector bundles are on different (mostly incomparable) kinds of bases.
In [Reference Jun, Mincheva and Tolliver18], we defined tropical vector bundles algebraically on general idempotent semiring schemes. These schemes are more general than the tropical schemes of Giansiracusa–Giansiracusa defined in [Reference Giansiracusa and Giansiracusa13]. In this setting, we define vector bundles as locally free sheaves of finite rank. There we observe that vector bundles globally split as sum of line bundles.
In [Reference Khan and Maclagan22], Khan and Maclagan and independently in [Reference Kaveh and Manon21], Kaveh and Manon propose a different definition of a toric vector bundle on a tropical toric variety. This combinatorial approach is inspired by the observation that tropical linear spaces correspond to (valuated) matroids (A matroid is a combinatorial abstraction of linear independence. See [Reference Oxley26]. We refer the reader whose background is in algebraic geometry to [Reference Katz20]). Roughly speaking, a tropical toric vector bundle in the sense of Khan and Maclagan on a tropical toric variety associated with a fan Δ is a triple ![]() $(\mathcal{M},\mathcal{G},\{E^\rho(j)\})$, where
$(\mathcal{M},\mathcal{G},\{E^\rho(j)\})$, where ![]() $\mathcal{M}$ is a (simple) valuated matroid on a ground set
$\mathcal{M}$ is a (simple) valuated matroid on a ground set ![]() $\mathcal{G}$, and
$\mathcal{G}$, and ![]() $\{E^\rho(j)\}$ is a collection of flats of the underlying matroid
$\{E^\rho(j)\}$ is a collection of flats of the underlying matroid ![]() $\underline{\mathcal{M}}$ with some compatibility condition analogous to compatibility condition of the filtrations in Klyachko’s classification of toric vector bundles [Reference Aleksander1, Theorem 2.2.1]. A more general case is defined by using embedded tropicalization and restriction of tropical toric vector bundle. The tropical toric vector bundles of Khan and Maclagan (in the case of trivial valuated matroid structure) are the same as the Kaveh and Manon’s toric matroid bundles.
$\underline{\mathcal{M}}$ with some compatibility condition analogous to compatibility condition of the filtrations in Klyachko’s classification of toric vector bundles [Reference Aleksander1, Theorem 2.2.1]. A more general case is defined by using embedded tropicalization and restriction of tropical toric vector bundle. The tropical toric vector bundles of Khan and Maclagan (in the case of trivial valuated matroid structure) are the same as the Kaveh and Manon’s toric matroid bundles.
The biggest difference with the present work is the information used to glue the vector bundle out of local data. In this work, the group of transition functions of our tropical toric vector bundles is the tropical ![]() $GL_n(\mathbb{T})$, which consists of invertible n × n matrices which are isomorphic to
$GL_n(\mathbb{T})$, which consists of invertible n × n matrices which are isomorphic to ![]() $S_n \lt imes \mathbb{R}^n$. In [Reference Khan and Maclagan22], the authors use the data of the flats of a valuated matroid, i.e., tropical subspaces, and a Klyachko-like filtration and thus obtain non-trivial tropical toric vector bundles.
$S_n \lt imes \mathbb{R}^n$. In [Reference Khan and Maclagan22], the authors use the data of the flats of a valuated matroid, i.e., tropical subspaces, and a Klyachko-like filtration and thus obtain non-trivial tropical toric vector bundles.
Another definition of tropical vector bundles is given in [Reference Allermann2]; the base for these bundles are tropical varieties (as polyhedral complexes). They are defined as principal ![]() $GL_n(\mathbb{T})$ bundles over a topological space. With this definition all vector bundles on a simply connected tropical variety are trivial. In [Reference Gross, Ulirsch and Zakharov15], the base of the vector bundle is a tropical curve (as a metric graph). A vector bundle on Γ is a
$GL_n(\mathbb{T})$ bundles over a topological space. With this definition all vector bundles on a simply connected tropical variety are trivial. In [Reference Gross, Ulirsch and Zakharov15], the base of the vector bundle is a tropical curve (as a metric graph). A vector bundle on Γ is a ![]() $S_n \lt imes \mathcal H$ Γ-torsor on Γ, where
$S_n \lt imes \mathcal H$ Γ-torsor on Γ, where ![]() $\mathcal H$ is the sheaf of real-valued harmonic functions with integer slopes on Γ. These two definitions agree when we consider the base as a topological space.
$\mathcal H$ is the sheaf of real-valued harmonic functions with integer slopes on Γ. These two definitions agree when we consider the base as a topological space.
Note that while metric graphs are a type of ‘tropical curves’, they employ an analytic approach to tropical geometry. Comparing these vector bundles to the algebraic ones in [Reference Jun, Mincheva and Tolliver18] or [Reference Khan and Maclagan22] and [Reference Kaveh and Manon21] requires an analogue of rigid-analytic methods to tropical scheme theory which is only partially developed. Notably, the topology on the base space in the cases considered is different leading to different incomparable notions of vector bundles.
Yet another approach to a notion of vector bundles over semirings focuses on the impact of the choice of (Grothendieck) topology on the base space. In [Reference Borger and Jun6], Borger and the first author study the module theory over semirings and show that while not all of the classical definitions of vector bundles agree over semirings, all definitions of line bundle agree. In particular, for a module M over a semiring R, the following three are equivalent: (1) M is Zariski-locally free of rank 1, (2) M is fpqc-locally free of rank 1, and (3) M is invertible.
Our previous results in [Reference Jun, Mincheva and Tolliver18] do not cover the case of equivariant vector bundles. In particular, while we show that a tropical vector bundle globally splits as sum of line bundles, we do not know if this happens equivariantly in the case of tropical toric vector bundles.
In this paper, we define toric vector bundles over a semiring in a purely algebraic way, and we show they equivariantly split as a sum of line bundles and show that we have a classification analogous to Klyachko’s classification of toric vector bundles in [Reference Aleksander1]. At the end, we briefly discuss how our work is related to the notion of tropical vector bundles by Khan and Maclagan [Reference Khan and Maclagan22].
1.1. Summary of results
In this paper, we begin by confirming that the natural correspondence between locally free sheaves and geometric vector bundles still hold in the semiring setting. One may easily modify the classical proofs for schemes (over rings) to prove the correspondence in the context of semirings, but we include sketches of some proofs for the readers who are not familiar with commutative algebra of semirings.
We introduce a notion of the functor of points of a locally free sheaf ![]() $\mathcal{F}$ of a scheme over a semiring R as follows (definition 3.14): for an R-algebra A and a morphism
$\mathcal{F}$ of a scheme over a semiring R as follows (definition 3.14): for an R-algebra A and a morphism ![]() $x:\operatorname{Spec} A \to X$, we define the fibre
$x:\operatorname{Spec} A \to X$, we define the fibre ![]() $\mathcal{F}_x$ as
$\mathcal{F}_x$ as
In other words, ![]() $\mathcal{F}_x$ is the global sections of the pullback
$\mathcal{F}_x$ is the global sections of the pullback ![]() $x^*\mathcal{F}$ of
$x^*\mathcal{F}$ of ![]() $\mathcal{F}$ along x. Then we define the set:
$\mathcal{F}$ along x. Then we define the set:
 \begin{equation*}
\mathcal{F}(A):=\bigsqcup_{x \in X(A)}\mathcal{F}_x,
\end{equation*}
\begin{equation*}
\mathcal{F}(A):=\bigsqcup_{x \in X(A)}\mathcal{F}_x,
\end{equation*} where ![]() $X(A)=\operatorname{Hom}(\operatorname{Spec} A, X)$, the set of A-rational points of X. The functor of points of
$X(A)=\operatorname{Hom}(\operatorname{Spec} A, X)$, the set of A-rational points of X. The functor of points of ![]() $\mathcal{F}$ is the functor sending an R-algebra A to
$\mathcal{F}$ is the functor sending an R-algebra A to ![]() $\mathcal{F}(A)$ and an R-algebra morphism
$\mathcal{F}(A)$ and an R-algebra morphism ![]() $f:A \to B$ to the morphism
$f:A \to B$ to the morphism ![]() $\mathcal{F}(A) \to \mathcal{F}(B)$ given by
$\mathcal{F}(A) \to \mathcal{F}(B)$ given by ![]() $v \mapsto f^*(v)$, where
$v \mapsto f^*(v)$, where ![]() $f^*(v) \in \mathcal{F}_{f^*(x)}$ is the pullback of the global section v along
$f^*(v) \in \mathcal{F}_{f^*(x)}$ is the pullback of the global section v along ![]() $f^*:\operatorname{Spec} B \to \operatorname{Spec} A$ (see remark 3.13). With this definition in mind, we prove our first main result.
$f^*:\operatorname{Spec} B \to \operatorname{Spec} A$ (see remark 3.13). With this definition in mind, we prove our first main result.
Theorem A (corollary 3.16)
The functor of points of a geometric vector bundle on a scheme X over a semiring R is the same as that of the corresponding locally free sheaf on a scheme X over a semiring R.
We define equivariant vector bundles on a scheme X over a semiring R by using the functor of points of a locally free sheaf (definition 4.1). It is well-known that any vector bundle on an affine toric variety is trivial [Reference Gubeladze16] and that any toric vector bundle on an affine toric variety is equivariantly trivializable [Reference Payne27, Proposition 2.2]. We prove that a similar result holds for schemes over an idempotent semifield under irreducibility assumption.
Theorem B (theorem 5.17)
Let X be an irreducible scheme over an idempotent semifield K and G be an irreducible algebraic group over K acting on X. Let E be a G-equivariant vector bundle on X which is trivial as a vector bundle. Then E is a direct sum of equivariant line bundles.
The above theorem is a consequence of several results. The first such result is that the functor of points of a scheme over an idempotent semiring is characterized by its values at irreducible idempotent semirings (proposition 5.3). Another aspect of the theory that heavily relies on working over idempotent semifields is irreducibility. More precisely, if X and Y are irreducible schemes over an idempotent semifield R, then ![]() $X\times_R Y$ is irreducible (proposition 5.13). This clearly fails for schemes over
$X\times_R Y$ is irreducible (proposition 5.13). This clearly fails for schemes over ![]() $\mathbb{Z}$. We also make use of the fact that every invertible matrix with entries in a zero-sum-free semiring is a product of a diagonal matrix and a permutation matrix (corollary 2.14). As a consequence, we prove that any equivariant vector bundle on a toric scheme X over an idempotent semifield, which is trivial as a vector bundle, equivariantly splits as a sum of equivariant line bundles.
$\mathbb{Z}$. We also make use of the fact that every invertible matrix with entries in a zero-sum-free semiring is a product of a diagonal matrix and a permutation matrix (corollary 2.14). As a consequence, we prove that any equivariant vector bundle on a toric scheme X over an idempotent semifield, which is trivial as a vector bundle, equivariantly splits as a sum of equivariant line bundles.
In §6, we classify equivariant vector bundles, which will be used later to prove a version of Klyachko’s classification of toric vector bundles in the setting of an idempotent semifield. We first show that analogously to the results for schemes over ![]() $\mathbb{Z}$ we have a natural isomorphism for schemes over a semiring or a monoid K:
$\mathbb{Z}$ we have a natural isomorphism for schemes over a semiring or a monoid K:
where ![]() $\text{GL}_1=\operatorname{Spec} K[t,t^{-1}]$. This allows us to go back and forth between morphisms and global sections.
$\text{GL}_1=\operatorname{Spec} K[t,t^{-1}]$. This allows us to go back and forth between morphisms and global sections.
Let K be a semiring or monoid, X be a scheme over K, and G be a group scheme over K acting on X. We say a map ![]() $u:G \times_KX \to \text{GL}_1$ is principal if for any K-algebra A and for
$u:G \times_KX \to \text{GL}_1$ is principal if for any K-algebra A and for ![]() $(g,h,x) \in (G\times_KG\times_KX)(A)$, the following holds:
$(g,h,x) \in (G\times_KG\times_KX)(A)$, the following holds:
Then, we prove the following correspondence.
Theorem C (proposition 6.8)
With the same notation as above, there is a one-to-one correspondence between
and
Moreover, this correspondence is a group isomorphism, where the first set is viewed as a group under tensor product, (Proposition 4.3 ensures that the first set is a group) and the second is a group under point-wise multiplication.
In §7, we explore how we can glue equivariant vector bundles on affine subschemes to obtain an equivariant vector bundle on a scheme. It turns out that the only obstruction to gluing is each affine subscheme has to be closed under the G-action (lemma 7.1 and proposition 7.2). As a consequence, we prove the following, an equivariant version of our previous result on vector bundles in [Reference Jun, Mincheva and Tolliver18].
Theorem D (theorem 7.4)
Let X be a toric scheme over an idempotent semifield R, and let G be the corresponding torus. Let E be a G-equivariant vector bundle on X. Then there are unique (up to permutation) equivariant line bundles ![]() $L_1, \ldots, L_n$ such that
$L_1, \ldots, L_n$ such that ![]() $E = L_1 \oplus \ldots \oplus L_n$ (as G-equivariant vector bundles).
$E = L_1 \oplus \ldots \oplus L_n$ (as G-equivariant vector bundles).
We prove that the G-action on an equivariant vector bundle is determined by the action on the torus (proposition 7.8). To introduce our next result, let R be an idempotent semifield and let X be a toric scheme over R. We denote by G the corresponding torus and by Λ the dual lattice and Δ be the fan corresponding to X. Based on the isomorphism (1), we further prove (proposition 6.15 and lemma 7.11) that there is a group homomorphism from Λ to ![]() $\operatorname{Pic}_G(X)$, the group of isomorphism classes of G-equivariant line bundles on X and characterize its kernel (proposition 7.13). As a result, we prove the following.
$\operatorname{Pic}_G(X)$, the group of isomorphism classes of G-equivariant line bundles on X and characterize its kernel (proposition 7.13). As a result, we prove the following.
Theorem E (theorem 7.14)
With the same notation as above, there is an exact sequence of abelian groups
 \begin{equation*}
0 \rightarrow \bigcap_{\sigma \in \Delta} (\Lambda \cap \sigma^\vee)^\perp \rightarrow \Lambda \rightarrow \mathrm{Pic}_G(X) \rightarrow \mathrm{Pic}(X) \rightarrow 0,
\end{equation*}
\begin{equation*}
0 \rightarrow \bigcap_{\sigma \in \Delta} (\Lambda \cap \sigma^\vee)^\perp \rightarrow \Lambda \rightarrow \mathrm{Pic}_G(X) \rightarrow \mathrm{Pic}(X) \rightarrow 0,
\end{equation*} where ![]() $\operatorname{Pic}_G(X) \to \operatorname{Pic}(X)$ is the forgetful map.
$\operatorname{Pic}_G(X) \to \operatorname{Pic}(X)$ is the forgetful map.
We note that if the rays of σ span ![]() $\Lambda_{\mathbb{R}}$ then
$\Lambda_{\mathbb{R}}$ then  $\bigcap_{\sigma \in \Delta} (\Lambda \cap \sigma^\vee)^\perp$ is 0. In this case, we obtain the semiring analog of the classical result for tropic varieties. More precisely, we get the first short exact sequence in [Reference Fulton12, Proposition 1].
$\bigcap_{\sigma \in \Delta} (\Lambda \cap \sigma^\vee)^\perp$ is 0. In this case, we obtain the semiring analog of the classical result for tropic varieties. More precisely, we get the first short exact sequence in [Reference Fulton12, Proposition 1].
In §8, we prove a version of Klyachko’s classification on toric vector bundles in our setting. Thanks to theorem D, classifying toric vector bundles on the toric scheme X over an idempotent semifield associated with a fan Δ reduces to classifying toric line bundles on X.
Let Λ be the dual lattice. We first prove that toric line bundles on X are in one-to-one correspondence with families of elements ![]() $[u_{\sigma}] \in \Lambda/(\Lambda\cap \sigma^\vee)^\perp$ indexed by cones satisfying some compatibility condition (proposition 8.4), which we call Klyachko families (definition 8.8).
$[u_{\sigma}] \in \Lambda/(\Lambda\cap \sigma^\vee)^\perp$ indexed by cones satisfying some compatibility condition (proposition 8.4), which we call Klyachko families (definition 8.8).
To turn this into a version of Klyachko’s classification theorem, we define an n-dimensional Δ-Klyachko space over an idempotent semifield K as a free K-module E of rank n with collections of decreasing filtrations ![]() $\{E^\rho(i)\}_{i\in \mathbb{Z}}$ indexed by the rays of Δ, satisfying some compatibility condition analogous to Klyachko’s theorem (definition 8.12). Then, we prove an equivalence between isomorphism classes of n-dimensional Δ-Klyachko spaces over an idempotent semifield K and Sn-orbits of n-tuples of Klyachko families (lemma 8.14). By appealing to these results, we prove the following.
$\{E^\rho(i)\}_{i\in \mathbb{Z}}$ indexed by the rays of Δ, satisfying some compatibility condition analogous to Klyachko’s theorem (definition 8.12). Then, we prove an equivalence between isomorphism classes of n-dimensional Δ-Klyachko spaces over an idempotent semifield K and Sn-orbits of n-tuples of Klyachko families (lemma 8.14). By appealing to these results, we prove the following.
Theorem F (theorem 8.15)
Let K be an idempotent semifield. Let XK be the toric scheme over K associated with a fan Δ. The set of isomorphism classes of toric vector bundles on XK is in one-to-one correspondence with the set of isomorphism classes of Δ-Klyachko spaces over K.
Finally, we note in remark 8.16 that a Δ-Klyachko space is a valuated matroid satisfying a certain compatibility condition, and that it is a tropical vector bundle in the sense of Khan and Maclagan in [Reference Khan and Maclagan22] whose underlying matroid is free.
1.2. Organization of the paper
We begin in §2 by reviewing some basic definitions and propositions needed for the paper.
In §3, we prove that the correspondence between geometric vector bundles and locally free sheaves is still valid in the setting of semirings. We then introduce the functor of points of a locally free sheaf and prove theorem A.
In §4, we define equivariant vector bundles via functor of points perspective.
In §5, we study irreducibility and equivariant bundles on irreducible schemes over an idempotent semifield. We then prove theorem B.
In §6, we classify equivariant bundles and prove theorem C.
In §7, we prove theorems D and E.
In §8, we prove theorem F, a tropical version of Klyachko’s classification theorem.
In Appendix A, we prove some basic results connecting toric varieties, toric monoid schemes, and toric schemes over ![]() $\mathbb{T}$.
$\mathbb{T}$.
In Appendix B, we prove that Sn can be seen as a scheme over ![]() $\mathbb{N}$.
$\mathbb{N}$.
2. Preliminaries
2.1. Toric vector bundles
We refer the reader to [Reference Fulton12] or [Reference Cox, Little and Schenck9] for standard notation and background on toric varieties. We denote by N a lattice and by ![]() $\Lambda= \operatorname{Hom}_{\mathbb{Z}}(N, \mathbb{Z})$ its dual, and by
$\Lambda= \operatorname{Hom}_{\mathbb{Z}}(N, \mathbb{Z})$ its dual, and by ![]() $\Lambda_{\mathbb{R}}$ and
$\Lambda_{\mathbb{R}}$ and ![]() $N_{\mathbb{R}}$ the dual vector spaces
$N_{\mathbb{R}}$ the dual vector spaces ![]() $\Lambda\otimes_{\mathbb{Z}}\mathbb{R}$ and
$\Lambda\otimes_{\mathbb{Z}}\mathbb{R}$ and ![]() $N\otimes_{\mathbb{Z}}\mathbb{R}$. We call Λ the character lattice. Given an isomorphism
$N\otimes_{\mathbb{Z}}\mathbb{R}$. We call Λ the character lattice. Given an isomorphism ![]() $\Lambda \cong \mathbb{Z}^n$, every point
$\Lambda \cong \mathbb{Z}^n$, every point ![]() $u =(u_1, \dots, u_n)$ in Λ gives rise to a character (group homomorphism)
$u =(u_1, \dots, u_n)$ in Λ gives rise to a character (group homomorphism)
where Gk is an algebraic torus over a field k. When k is a semifield a point in Λ similarly gives rise to a homomorphism of groups ![]() $(k^\times)^n \rightarrow k^\times$.
$(k^\times)^n \rightarrow k^\times$.
We will denote by σ a strongly convex rational polyhedral cone in ![]() $N_{\mathbb{R}}$, that is,
$N_{\mathbb{R}}$, that is,
 \begin{equation*}
\sigma = \sum\limits_{i=1}^{r}\mathbb{R}_{\geq 0}v_i, \quad v_i \in N.
\end{equation*}
\begin{equation*}
\sigma = \sum\limits_{i=1}^{r}\mathbb{R}_{\geq 0}v_i, \quad v_i \in N.
\end{equation*} All the cones we will consider from now on will be strongly convex rational polyhedral. We denote by ![]() $\sigma^\vee$ the dual cone of σ:
$\sigma^\vee$ the dual cone of σ:
A fan Δ is a finite collection of cones σ in ![]() $N_{\mathbb{R}}$ such that each face of σ is also a cone of Δ and the intersection of two cones of Δ is a face of both.
$N_{\mathbb{R}}$ such that each face of σ is also a cone of Δ and the intersection of two cones of Δ is a face of both.
We recall the definition of a toric vector bundle. Let X be a toric variety (with torus G). We say that ![]() $\mathcal{E}$ is a toric vector bundle on X if it is a vector bundle, together with an action of G, compatible with the action on X.
$\mathcal{E}$ is a toric vector bundle on X if it is a vector bundle, together with an action of G, compatible with the action on X.
We recall a classification of toric vector bundles.
Theorem 2.1 Klyachko’s classification theorem
Let k be a field. The category of toric vector bundles on ![]() $X(\Delta)_k$ is naturally equivalent to the category of finite-dimensional k-vector spaces E with collections of decreasing filtrations
$X(\Delta)_k$ is naturally equivalent to the category of finite-dimensional k-vector spaces E with collections of decreasing filtrations ![]() $\{E^\rho(n)\}$ indexed by the rays of Δ, satisfying the following compatibility condition: For each cone
$\{E^\rho(n)\}$ indexed by the rays of Δ, satisfying the following compatibility condition: For each cone ![]() $\sigma \in \Delta$, there exists a decomposition
$\sigma \in \Delta$, there exists a decomposition  $E=\bigoplus \limits_{[u] \in \Lambda_{\sigma}} E_{[u]}$ such that
$E=\bigoplus \limits_{[u] \in \Lambda_{\sigma}} E_{[u]}$ such that
 \begin{equation*}
E^\rho(i) = \sum_{\left \lt [u],v_\rho\right \gt \geq i}E_{[u]},
\end{equation*}
\begin{equation*}
E^\rho(i) = \sum_{\left \lt [u],v_\rho\right \gt \geq i}E_{[u]},
\end{equation*} for every ![]() $\rho \preceq \sigma$ and
$\rho \preceq \sigma$ and ![]() $i \in \mathbb{Z}$, where
$i \in \mathbb{Z}$, where ![]() $\Lambda_{\sigma}:=\Lambda/(\sigma^\perp \cap \Lambda)$.
$\Lambda_{\sigma}:=\Lambda/(\sigma^\perp \cap \Lambda)$.
2.2. Monoids and monoid schemes
One may mimic the construction of schemes to define monoid schemes. Alternatively, one may take a functor of points approach to define the category of affine monoid schemes as the opposite category of monoids, and monoid schemes as (Zariski) sheaves on the category of monoids. As in the case of schemes, these two definitions are equivalent.
In this paper, by a monoid, we mean a commutative (multiplicative) monoid A. By a pointed monoid, which means that there exists an absorbing element ![]() $0_A \in A$, that is,
$0_A \in A$, that is, ![]() $0_A\cdot a=0_A$ for all
$0_A\cdot a=0_A$ for all ![]() $a \in A$.
$a \in A$.
By a module over a monoid A, we mean a set M together with a map ![]() $\phi: A\times M \to M$, defined by
$\phi: A\times M \to M$, defined by ![]() $\phi(a, m) = am$, where
$\phi(a, m) = am$, where ![]() $1m = m$ and
$1m = m$ and ![]() $(ab)m=a(bm)$.
$(ab)m=a(bm)$.
The tensor product ![]() $M \otimes_A N$ of two modules
$M \otimes_A N$ of two modules ![]() $M, N$ of a monoid A is defined to be the quotient of M × N by the equivalence relation generated by
$M, N$ of a monoid A is defined to be the quotient of M × N by the equivalence relation generated by ![]() $(am, n) \sim (m, an)$, for all
$(am, n) \sim (m, an)$, for all ![]() $a\in A$,
$a\in A$, ![]() $m\in M$ and
$m\in M$ and ![]() $n\in N$. As usual we denote the equivalence class on (m, n) by
$n\in N$. As usual we denote the equivalence class on (m, n) by ![]() $m\otimes n$. If M and N are two pointed modules of A with distinguished points m 0 and n 0, respectively, then their tensor product is
$m\otimes n$. If M and N are two pointed modules of A with distinguished points m 0 and n 0, respectively, then their tensor product is
For properties of the tensor product of (pointed) monoids, we refer the reader to [Reference Deitmar11].
Denote by ![]() $\mathbb{F}_1$ the initial object in the category of (pointed) monoids. We interpret it as a pointed multiplicative monoid with one element which we call 1 and absorbing element 0. A (pointed) monoid is automatically an
$\mathbb{F}_1$ the initial object in the category of (pointed) monoids. We interpret it as a pointed multiplicative monoid with one element which we call 1 and absorbing element 0. A (pointed) monoid is automatically an ![]() $\mathbb{F}_1$-module.
$\mathbb{F}_1$-module.
By an ![]() $\mathbb{F}_1$-algebra, we mean a pointed monoid. An
$\mathbb{F}_1$-algebra, we mean a pointed monoid. An ![]() $\mathbb{F}_1$-algebra A is said to be irreducible if the product of non-nilpotents is not nilpotent.
$\mathbb{F}_1$-algebra A is said to be irreducible if the product of non-nilpotents is not nilpotent.
For a monoid A, a nonempty subset ![]() $I\subseteq A$ is said to be an ideal if
$I\subseteq A$ is said to be an ideal if ![]() $AI \subseteq I$. An ideal I is said to be prime if A − I is a multiplicative nonempty subset of A, and maximal if I is a proper ideal (i.e., I ≠ A) which is not contained in any other proper ideal.
$AI \subseteq I$. An ideal I is said to be prime if A − I is a multiplicative nonempty subset of A, and maximal if I is a proper ideal (i.e., I ≠ A) which is not contained in any other proper ideal.
We can define the prime spectrum ![]() $\operatorname{Spec} A$ of a monoid A as the set of all prime ideals of A equipped with the Zariski topology. The set
$\operatorname{Spec} A$ of a monoid A as the set of all prime ideals of A equipped with the Zariski topology. The set ![]() $\{D(f)\}_{f \in A}$ forms an open basis of
$\{D(f)\}_{f \in A}$ forms an open basis of ![]() $\operatorname{Spec} A$, where
$\operatorname{Spec} A$, where ![]() $D(f):=\{\mathfrak{p} \in \operatorname{Spec} A \mid f \not\in \mathfrak{p}\}$.
$D(f):=\{\mathfrak{p} \in \operatorname{Spec} A \mid f \not\in \mathfrak{p}\}$.
A monoid scheme (or ![]() $\mathbb{F}_1$-scheme) is defined to be a topological space equipped with a structure sheaf of monoids locally isomorphic to affine monoid schemes
$\mathbb{F}_1$-scheme) is defined to be a topological space equipped with a structure sheaf of monoids locally isomorphic to affine monoid schemes ![]() $(\operatorname{Spec} A, \mathcal{O}_{\operatorname{Spec} A})$. We refer the reader to [Reference Jun, Mincheva and Tolliver17, §2] for the precise definitions and details.
$(\operatorname{Spec} A, \mathcal{O}_{\operatorname{Spec} A})$. We refer the reader to [Reference Jun, Mincheva and Tolliver17, §2] for the precise definitions and details.
A special class of monoid schemes called toric monoid schemes (or toric ![]() $\mathbb{F}_1$-schemes) can be obtained from fans. A toric monoid scheme is locally isomorphic to
$\mathbb{F}_1$-schemes) can be obtained from fans. A toric monoid scheme is locally isomorphic to ![]() $\operatorname{Spec} A$, where A is a toric monoid (By a toric monoid, we mean the monoid obtained from a cone giving rise to an affine toric variety). The fan tells us how to glue the affine pieces corresponding to each cone of the fan. For more details, we refer the reader to [Reference Cortiñas, Haesemeyer, Walker and Weibel8].
$\operatorname{Spec} A$, where A is a toric monoid (By a toric monoid, we mean the monoid obtained from a cone giving rise to an affine toric variety). The fan tells us how to glue the affine pieces corresponding to each cone of the fan. For more details, we refer the reader to [Reference Cortiñas, Haesemeyer, Walker and Weibel8].
2.3. Semirings, toric schemes over semirings, and vector bundles
Definition 2.2. A semiring is a nonempty set R with two binary operations ![]() $(+,\cdot)$ satisfying:
$(+,\cdot)$ satisfying:
•
 $(R,+)$ is a commutative monoid with identity element 0 R
$(R,+)$ is a commutative monoid with identity element 0 R•
 $(R,\cdot)$ is a monoid with identity element 1R
$(R,\cdot)$ is a monoid with identity element 1R• For any
 $a,b,c \in R$:
$a,b,c \in R$:  $a(b+c) = ab+ac$
$a(b+c) = ab+ac$•
 $1_R \neq 0_R$ and
$1_R \neq 0_R$ and  $a\cdot 0_R = 0_R$ for all
$a\cdot 0_R = 0_R$ for all  $a \in R$
$a \in R$
In this paper, all semirings are assumed to be commutative, i.e., ![]() $(R,\cdot)$ is a commutative monoid.
$(R,\cdot)$ is a commutative monoid.
R is said to be zero-sum free if ![]() $a+b=0$ implies
$a+b=0$ implies ![]() $a=b=0$ for all
$a=b=0$ for all ![]() $a,b \in R$.
$a,b \in R$.
A semifield is a semiring in which all non-zero elements have a multiplicative inverse.
We will denote by ![]() $\mathbb{B}$ the semifield with two elements
$\mathbb{B}$ the semifield with two elements ![]() $\{1,0\}$, where 1 is the multiplicative identity, 0 is the additive identity and
$\{1,0\}$, where 1 is the multiplicative identity, 0 is the additive identity and ![]() $1+1 = 1$. The tropical semifield, denoted
$1+1 = 1$. The tropical semifield, denoted ![]() $\mathbb{T}$, is the set
$\mathbb{T}$, is the set ![]() $\mathbb{R} \cup \{-\infty\} $ with the + operation to be the maximum and the · operation to be the usual addition, with
$\mathbb{R} \cup \{-\infty\} $ with the + operation to be the maximum and the · operation to be the usual addition, with ![]() $-\infty = 0_{\mathbb{T}}$.
$-\infty = 0_{\mathbb{T}}$.
Definition 2.3. An affine semiring scheme is the prime spectrum ![]() $X=\operatorname{Spec} R$ of some semiring R, equipped with a structure sheaf
$X=\operatorname{Spec} R$ of some semiring R, equipped with a structure sheaf ![]() $\mathcal{O}_X$. A locally semiringed space is a topological space with a sheaf of semirings such that the stalk at each point has a unique maximal ideal. A semiring scheme is a locally semiringed space that is locally isomorphic to an affine semiring scheme (As we noted in the introduction, this is equivalent to the functor of points approach).
$\mathcal{O}_X$. A locally semiringed space is a topological space with a sheaf of semirings such that the stalk at each point has a unique maximal ideal. A semiring scheme is a locally semiringed space that is locally isomorphic to an affine semiring scheme (As we noted in the introduction, this is equivalent to the functor of points approach).
Remark 2.4. In [Reference Giansiracusa and Giansiracusa13] J. Giansiracusa and N. Giansiracusa propose a special case of the semiring schemes called tropical schemes in such a way that the tropicalization of an algebraic variety can be understood as a set of ![]() $\mathbb{T}$-rational points of a tropical scheme.
$\mathbb{T}$-rational points of a tropical scheme.
Definition 2.5. By a toric scheme X over a ring (resp. semiring) R, we mean a scheme containing an algebraic torus ![]() $(R^\times)^n$ as an open dense subset, such that the action of the torus on itself extends to the whole scheme.
$(R^\times)^n$ as an open dense subset, such that the action of the torus on itself extends to the whole scheme.
Toric schemes over idempotent semirings are intimately related to monoid schemes, in fact they arise from monoid schemes via base change. We make this relation precise.
Definition 2.6. For any ring (resp. semiring) R we define ![]() $M\otimes_{\mathbb{F}_1}R$ to be the monoid ring (resp. semiring)
$M\otimes_{\mathbb{F}_1}R$ to be the monoid ring (resp. semiring) ![]() $R[M]$, where we identify 0 M and 0 R. This defines a functor from the category of monoids to the category of R-algebras, sending M to
$R[M]$, where we identify 0 M and 0 R. This defines a functor from the category of monoids to the category of R-algebras, sending M to ![]() $ R[M]$. There is also a natural functor (forgetful functor)
$ R[M]$. There is also a natural functor (forgetful functor) ![]() $\mathfrak{F}$ from the category of rings (resp. semirings) to the category of monoids sending a ring (resp. semiring) A to
$\mathfrak{F}$ from the category of rings (resp. semirings) to the category of monoids sending a ring (resp. semiring) A to ![]() $(A,\times)$, the underlying multiplicative monoid with 0 A. There is an adjunction:
$(A,\times)$, the underlying multiplicative monoid with 0 A. There is an adjunction:
This gives rise to a functor ![]() $-\otimes_{\mathbb{F}_1}R$ from the category of monoid schemes to the category of schemes (resp. semiring schemes) sending X to
$-\otimes_{\mathbb{F}_1}R$ from the category of monoid schemes to the category of schemes (resp. semiring schemes) sending X to ![]() $X_R:=X\otimes_{\mathbb{F}_1}R$. One can find the details of that construction in [Reference Giansiracusa and Giansiracusa13, Section 2.3].
$X_R:=X\otimes_{\mathbb{F}_1}R$. One can find the details of that construction in [Reference Giansiracusa and Giansiracusa13, Section 2.3].
From Appendix A, one can see that a toric scheme X (whether over a ring or a semiring) is purely determined by the combinatorial data of a fan.
Remark 2.7. An affine toric scheme ![]() $X(\sigma)$ over a ring (resp. semiring) R is determined by the combinatorial data of a cone σ in a lattice
$X(\sigma)$ over a ring (resp. semiring) R is determined by the combinatorial data of a cone σ in a lattice ![]() $N \cong \mathbb{Z}^n$. Denote by M the dual lattice of N. Now,
$N \cong \mathbb{Z}^n$. Denote by M the dual lattice of N. Now, ![]() $X(\sigma)$ is the affine toric scheme (resp. semiring scheme)
$X(\sigma)$ is the affine toric scheme (resp. semiring scheme) ![]() $\operatorname{Spec} R[\sigma^{\vee} \cap M]$. In particular, an affine toric scheme is isomorphic to the base change of the toric monoid scheme
$\operatorname{Spec} R[\sigma^{\vee} \cap M]$. In particular, an affine toric scheme is isomorphic to the base change of the toric monoid scheme ![]() $\operatorname{Spec} (\sigma^{\vee} \cap M)$. A toric scheme X over a ring (resp. semiring) R is determined by the combinatorial data of a fan Σ and is isomorphic to the base change of the toric monoid scheme determined by that fan.
$\operatorname{Spec} (\sigma^{\vee} \cap M)$. A toric scheme X over a ring (resp. semiring) R is determined by the combinatorial data of a fan Σ and is isomorphic to the base change of the toric monoid scheme determined by that fan.
Example 2.8. Let ![]() $R = \mathbb{T}[x, y]$. Then
$R = \mathbb{T}[x, y]$. Then ![]() $\operatorname{Spec} R$ is a toric scheme over
$\operatorname{Spec} R$ is a toric scheme over ![]() $\mathbb{T}$, which is the tropical analogue of the affine 2-space. In this case,
$\mathbb{T}$, which is the tropical analogue of the affine 2-space. In this case, ![]() $R = \mathbb{T}[M]$, where
$R = \mathbb{T}[M]$, where ![]() $M = \mathbb{N}^2 \cup \{0\}$.
$M = \mathbb{N}^2 \cup \{0\}$.
Definition 2.9. Let R be a semiring and M be an R-module.
(1) A subset
 $\{x_1,\dots,x_n\} \subseteq M$ is linearly independent if
$\{x_1,\dots,x_n\} \subseteq M$ is linearly independent if
 \begin{equation*}
\sum_{i=1}^na_ix_i = \sum_{i=1}^n b_ix_i
\end{equation*}
\begin{equation*}
\sum_{i=1}^na_ix_i = \sum_{i=1}^n b_ix_i
\end{equation*}implies that
 $a_i=b_i$ for all
$a_i=b_i$ for all  $i=1,\dots,n$.
$i=1,\dots,n$.(2) M is free of rank n if there exists a set
 $\{x_1,\dots,x_n\} $ of linearly independent generators of M over R.
$\{x_1,\dots,x_n\} $ of linearly independent generators of M over R.
One can easily see that if M is a free R-module of rank n, then ![]() $M\simeq R^n$ (as an R-module).
$M\simeq R^n$ (as an R-module).
We recall some results from [Reference Jun, Mincheva and Tolliver18] which will be used in this paper. We first recall the definition of idempotent pairs.
Definition 2.10. [Reference Jun, Mincheva and Tolliver18] Definition 3.6
Let R be a semiring. By an idempotent pair of R, we mean a pair (e, f) such that ![]() $e+f=1$ and ef = 0. An idempotent pair (e, f) is said to be trivial if
$e+f=1$ and ef = 0. An idempotent pair (e, f) is said to be trivial if ![]() $\{e,f\} = \{0,1\}$.
$\{e,f\} = \{0,1\}$.
Proposition 2.11. [Reference Jun, Mincheva and Tolliver18] Proposition 3.10
Let R be a semiring, ![]() $\operatorname{Spec} R$ is connected if and only if any idempotent pair of R is trivial.
$\operatorname{Spec} R$ is connected if and only if any idempotent pair of R is trivial.
Lemma 2.12. [Reference Jun, Mincheva and Tolliver18] Lemma 3.14
Let R be a zero-sum-free semiring with only trivial idempotent pairs, and M be a free module over R with basis ![]() $S\subseteq M$. Suppose
$S\subseteq M$. Suppose ![]() $M=P\oplus Q$. Then there exists a subset
$M=P\oplus Q$. Then there exists a subset ![]() $S'\subseteq S$ such that P is free with basis S ʹ and Q is free with basis
$S'\subseteq S$ such that P is free with basis S ʹ and Q is free with basis ![]() $S \setminus S'$.
$S \setminus S'$.
Proposition 2.13. [Reference Jun, Mincheva and Tolliver18] Proposition 3.18
Let R be a zero-sum-free semiring. If R has only trivial idempotent pairs, then one has the following split short exact sequence of groups which is natural in R:

where f is the diagonal map and g sends a matrix A to the unique permutation σ such that ![]() $A_{\sigma(i)i}\neq 0$ for all i.
$A_{\sigma(i)i}\neq 0$ for all i.
Proposition 2.14. [Reference Jun, Mincheva and Tolliver18] Corollary 3.19
Let R be a zero-sum free semiring. If R has only trivial idempotent pairs, then one has the following isomorphism of groups:
where Sn acts on ![]() $(R^\times)^n$ by permuting factors.
$(R^\times)^n$ by permuting factors.
Proposition 2.15. [Reference Jun, Mincheva and Tolliver18] Theorem 4.7
Let X be an irreducible semiring scheme that is locally isomorphic to ![]() $\operatorname{Spec} R$, where R is a zero-sum free semiring. Then any vector bundle of rank n on X is a direct sum of n copies of line bundles on X. Moreover, this decomposition is unique up to permuting summands.
$\operatorname{Spec} R$, where R is a zero-sum free semiring. Then any vector bundle of rank n on X is a direct sum of n copies of line bundles on X. Moreover, this decomposition is unique up to permuting summands.
Remark 2.16. In [Reference Jun, Mincheva and Tolliver18], Proposition 2.15 assumes that R has only trivial idempotent pairs, however, this follows from the irreducibility of X.
Let X be an irreducible monoid scheme. Suppose that X has an open affine cover ![]() $\mathcal{U}=\{U_\alpha\}$ such that any finite intersection of the sets Uα is isomorphic to the prime spectrum of a cancellative monoid (This condition is always satisfied with toric monoid schemes as in this case monoids are subsets of dual lattices. Also, all of our monoids are finitely generated by Gordan’s lemma).
$\mathcal{U}=\{U_\alpha\}$ such that any finite intersection of the sets Uα is isomorphic to the prime spectrum of a cancellative monoid (This condition is always satisfied with toric monoid schemes as in this case monoids are subsets of dual lattices. Also, all of our monoids are finitely generated by Gordan’s lemma).
For instance, when X is a toric scheme over ![]() $\mathbb{T}$, then the above condition holds.
$\mathbb{T}$, then the above condition holds.
We now define vector bundles on monoid and semiring schemes and give some relations between them.
Definition 2.18. Let X be a monoid scheme or a semiring scheme.
(1) A vector bundle on X is an
 $\mathcal{O}_X$-module
$\mathcal{O}_X$-module  $\mathcal{F}$ such that for each
$\mathcal{F}$ such that for each  $x \in X$, there exists an open neighborhood U of x and a finite set I such that
$x \in X$, there exists an open neighborhood U of x and a finite set I such that
 \begin{equation*}
\mathcal{F}|_{U} \simeq \bigoplus_{i \in I} \mathcal{O}_X|_U
\end{equation*}
\begin{equation*}
\mathcal{F}|_{U} \simeq \bigoplus_{i \in I} \mathcal{O}_X|_U
\end{equation*}as an
 $\mathcal{O}_X|_U$-module. A vector bundle
$\mathcal{O}_X|_U$-module. A vector bundle  $\mathcal{F}$ on X is said to be rank n if
$\mathcal{F}$ on X is said to be rank n if  $|I|=n$ for each open subset U.
$|I|=n$ for each open subset U.(2) We let
 $\mathbf{Vect}(X)$ be the category of vector bundles on X, and
$\mathbf{Vect}(X)$ be the category of vector bundles on X, and  $\mathbf{Vect}_n(X)$ be the full subcategory consisting of vector bundles of rank n on X.
$\mathbf{Vect}_n(X)$ be the full subcategory consisting of vector bundles of rank n on X.(3) We denote by
 $\operatorname{Pic}(X)$, the group of isomorphism classes of rank 1 vector bundles, i.e., line bundles on X.
$\operatorname{Pic}(X)$, the group of isomorphism classes of rank 1 vector bundles, i.e., line bundles on X.
Proposition 2.19. [Reference Jun, Mincheva and Tolliver18] Corollary 4.8
Let M be a cancellative monoid and K be an idempotent semifield. Then any vector bundle on ![]() $X=\operatorname{Spec} K[M]$ is trivial.
$X=\operatorname{Spec} K[M]$ is trivial.
Proposition 2.20. [Reference Jun, Mincheva and Tolliver18] Theorem 4.11
Let X be an irreducible monoid scheme satisfying condition 2.17, and K be an idempotent semifield. Then, there exists a natural bijection between ![]() $Vect_n(X)$ and
$Vect_n(X)$ and ![]() $Vect_n(X_K)$.
$Vect_n(X_K)$.
3. Equivalence between locally free sheaves and geometric vector bundles
In this section, we show that the one-to-one correspondence between isomorphism classes of geometric vector bundles and locally free sheaves is still valid for semirings. The proofs are almost identical to the case of rings, but we include them here for completeness. We then provide a definition of the functor of points of a locally free sheaf, which is equivalent to the functor of points of the corresponding geometric vector bundle.
In what follows, instead of saying a semiring scheme, we will simply say a scheme over ![]() $\mathbb{N}$. Equivalently, one can think of a semiring scheme as a scheme X with a structure map
$\mathbb{N}$. Equivalently, one can think of a semiring scheme as a scheme X with a structure map ![]() $X \to \operatorname{Spec} \mathbb{N}$.
$X \to \operatorname{Spec} \mathbb{N}$.
Let X be a scheme over ![]() $\mathbb{N}$. By
$\mathbb{N}$. By ![]() $\mathbb{A}^n_X$, we mean the scheme
$\mathbb{A}^n_X$, we mean the scheme ![]() $X\times_{\mathbb{N}} \mathbb{A}^n_{\mathbb{N}}$, where
$X\times_{\mathbb{N}} \mathbb{A}^n_{\mathbb{N}}$, where ![]() $\mathbb{A}^n_{\mathbb{N}}=\operatorname{Spec} \mathbb{N}[x_1,\dots,x_n]$.
$\mathbb{A}^n_{\mathbb{N}}=\operatorname{Spec} \mathbb{N}[x_1,\dots,x_n]$.
Definition 3.1. Let Y be a scheme over ![]() $\mathbb{N}$. A geometric vector bundle of rank n over Y is a scheme X over Y and a morphism
$\mathbb{N}$. A geometric vector bundle of rank n over Y is a scheme X over Y and a morphism ![]() $f:X \to Y$, together with an open covering
$f:X \to Y$, together with an open covering ![]() $\{U_i\}$ of Y, and isomorphisms:
$\{U_i\}$ of Y, and isomorphisms:
 \begin{equation}
\psi_i:f^{-1}(U_i)=X\times_YU_i \to \mathbb{A}^n_{U_i},
\end{equation}
\begin{equation}
\psi_i:f^{-1}(U_i)=X\times_YU_i \to \mathbb{A}^n_{U_i},
\end{equation} such that for any ![]() $i, j$ and for any open affine subset
$i, j$ and for any open affine subset ![]() $V=\operatorname{Spec} A \subseteq U_i \cap U_j$, the automorphism
$V=\operatorname{Spec} A \subseteq U_i \cap U_j$, the automorphism  $\psi=\psi_j \circ \psi_i^{-1}$ of
$\psi=\psi_j \circ \psi_i^{-1}$ of ![]() $\mathbb{A}_V^n=\operatorname{Spec} A[x_1,\dots,x_n]$ is given by a linear automorphism θ of
$\mathbb{A}_V^n=\operatorname{Spec} A[x_1,\dots,x_n]$ is given by a linear automorphism θ of ![]() $A[x_1,\dots,x_n]$.
$A[x_1,\dots,x_n]$.
Let ![]() $(X,f,\{U_i\},\{\psi_i\})$ and
$(X,f,\{U_i\},\{\psi_i\})$ and ![]() $(X',f',\{U_j'\},\{\psi_j\})$ be geometric vector bundles on a scheme Y over
$(X',f',\{U_j'\},\{\psi_j\})$ be geometric vector bundles on a scheme Y over ![]() $\mathbb{N}$. An isomorphism is an isomorphism
$\mathbb{N}$. An isomorphism is an isomorphism ![]() $g:X \to X'$ of underlying schemes X and X ʹ such that
$g:X \to X'$ of underlying schemes X and X ʹ such that
and X and ![]() $f:X \to Y$ together with the covering of Y consisting of
$f:X \to Y$ together with the covering of Y consisting of ![]() $\{U_i\}\cup\{U_j'\}$ and the isomorphisms ψi,
$\{U_i\}\cup\{U_j'\}$ and the isomorphisms ψi, ![]() $\psi'_j\circ g$ also gives a geometric vector bundle structure on X.
$\psi'_j\circ g$ also gives a geometric vector bundle structure on X.
Lemma 3.2. Let Y be a scheme over ![]() $\mathbb{N}$ and
$\mathbb{N}$ and ![]() $f:X \to Y$ be a geometric vector bundle of rank n. Then the following defines a locally free sheaf of rank n on Y: for each open
$f:X \to Y$ be a geometric vector bundle of rank n. Then the following defines a locally free sheaf of rank n on Y: for each open ![]() $U \subseteq Y$
$U \subseteq Y$
Proof. The proof follows mutatis mutandis as the one for schemes over rings.
Tensor algebras and symmetric algebras can be also constructed for semirings in the same way of those for rings. More precisely, let R be a semiring. Then tensor product ![]() $M\otimes_RN$ of R-modules M, N are defined as for rings. For more details, see [Reference Borger4] or [Reference Giansiracusa and Giansiracusa14]. Now, we let
$M\otimes_RN$ of R-modules M, N are defined as for rings. For more details, see [Reference Borger4] or [Reference Giansiracusa and Giansiracusa14]. Now, we let ![]() $\text{T}^0(M)=R$ and we inductively define
$\text{T}^0(M)=R$ and we inductively define
Define the tensor algebra of M to be  $\text{T} (M) = \bigoplus_{d\geq 0} \text{T}^d(M)$, where multiplication is determined by the following natural isomorphism (concatenation):
$\text{T} (M) = \bigoplus_{d\geq 0} \text{T}^d(M)$, where multiplication is determined by the following natural isomorphism (concatenation):
We proceed to define the symmetric algebra ![]() $\text{S} (M)$ as the quotient of
$\text{S} (M)$ as the quotient of ![]() $ \text{T} (M)$ by the equivalence relation generated by
$ \text{T} (M)$ by the equivalence relation generated by ![]() $ m_i \otimes m_j \sim m_j \otimes m_i$, for all mi,
$ m_i \otimes m_j \sim m_j \otimes m_i$, for all mi, ![]() $m_j \in M$. As in the case of rings, we have that
$m_j \in M$. As in the case of rings, we have that ![]() $\text{Sym}^d(M)$ is the quotient of
$\text{Sym}^d(M)$ is the quotient of ![]() $\text{T}^d(M)$ by the equivalence relation generated by the elements
$\text{T}^d(M)$ by the equivalence relation generated by the elements ![]() $m_1 \otimes \dots \otimes m_d \sim m_{\sigma(1)} \otimes \dots \otimes m_{\sigma(d)}$, for all
$m_1 \otimes \dots \otimes m_d \sim m_{\sigma(1)} \otimes \dots \otimes m_{\sigma(d)}$, for all ![]() $m_i\in M$ and σ a permutation on d elements. Thus we have
$m_i\in M$ and σ a permutation on d elements. Thus we have  $\text{Sym} (M) = \bigoplus_{d\geq 0} \text{Sym}^d(M)$.
$\text{Sym} (M) = \bigoplus_{d\geq 0} \text{Sym}^d(M)$.
Likewise, for an ![]() $\mathcal{O}_Y$-module
$\mathcal{O}_Y$-module ![]() $\mathcal{F}$ of a scheme Y over
$\mathcal{F}$ of a scheme Y over ![]() $\mathbb{N}$, the tensor algebra
$\mathbb{N}$, the tensor algebra ![]() $\text{T}(\mathcal{F})$ and symmetric algebra
$\text{T}(\mathcal{F})$ and symmetric algebra ![]() $\text{Sym}(\mathcal{F})$ can be defined similarly for rings, as the sheafification of the obvious presheaves.
$\text{Sym}(\mathcal{F})$ can be defined similarly for rings, as the sheafification of the obvious presheaves.
Next, let ![]() $\mathcal{F}$ be a quasi-coherent sheaf of algebras on a scheme Y over
$\mathcal{F}$ be a quasi-coherent sheaf of algebras on a scheme Y over ![]() $\mathbb{N}$. We let
$\mathbb{N}$. We let ![]() $\operatorname{Spec} \mathcal{F}$ be the scheme over
$\operatorname{Spec} \mathcal{F}$ be the scheme over ![]() $\mathbb{N}$ defined as follows: for each open subset
$\mathbb{N}$ defined as follows: for each open subset ![]() $U \subseteq Y$, we have an affine scheme
$U \subseteq Y$, we have an affine scheme ![]() $\operatorname{Spec} \mathcal{F}(U)$. The scheme
$\operatorname{Spec} \mathcal{F}(U)$. The scheme ![]() $\operatorname{Spec} \mathcal{F}$ is obtained by gluing these affine pieces. Note that there is a natural projection map
$\operatorname{Spec} \mathcal{F}$ is obtained by gluing these affine pieces. Note that there is a natural projection map
If ![]() $\mathcal{F}$ denotes a quasicoherent sheaf of modules, by
$\mathcal{F}$ denotes a quasicoherent sheaf of modules, by ![]() $\mathbf{V}(\mathcal{F})$, we will mean
$\mathbf{V}(\mathcal{F})$, we will mean ![]() $\operatorname{Spec}(\text{Sym}(\mathcal{F}))$.
$\operatorname{Spec}(\text{Sym}(\mathcal{F}))$.
Remark 3.3. Let ![]() $\mathcal{F}$ be a locally free sheaf of rank n on a scheme Y over
$\mathcal{F}$ be a locally free sheaf of rank n on a scheme Y over ![]() $\mathbb{N}$. Then the symmetric algebra
$\mathbb{N}$. Then the symmetric algebra ![]() $\text{Sym}(\mathcal{F})$ is also a locally free sheaf on Y. In fact, the question is local. Hence it is enough to show it when
$\text{Sym}(\mathcal{F})$ is also a locally free sheaf on Y. In fact, the question is local. Hence it is enough to show it when ![]() $M=R^n$ for some semiring R. But, in this case, clearly the symmetric algebra
$M=R^n$ for some semiring R. But, in this case, clearly the symmetric algebra ![]() $\text{Sym}(M)$ is a free R-module.
$\text{Sym}(M)$ is a free R-module.
In what follows by a scheme, we always mean a scheme over ![]() $\mathbb{N}$ (equivalently semiring schemes) unless otherwise stated.
$\mathbb{N}$ (equivalently semiring schemes) unless otherwise stated.
Let ![]() $\mathcal{F}$ be a locally free sheaf of rank n on a scheme Y. Let
$\mathcal{F}$ be a locally free sheaf of rank n on a scheme Y. Let ![]() $X=\mathbf{V}(\mathcal{F})$, with projection morphism
$X=\mathbf{V}(\mathcal{F})$, with projection morphism ![]() $f:X \to Y$ as in (5). For each open affine subset
$f:X \to Y$ as in (5). For each open affine subset ![]() $U \subseteq Y$ for which
$U \subseteq Y$ for which ![]() $\mathcal{F}|_U$ is free, choose a basis of
$\mathcal{F}|_U$ is free, choose a basis of ![]() $\mathcal{F}$, and let
$\mathcal{F}$, and let
be the isomorphism resulting from the identification of ![]() $\text{Sym}(\mathcal{F}(U))$ with
$\text{Sym}(\mathcal{F}(U))$ with ![]() $\mathcal{O}_Y(U)[x_1,\dots,x_n]$.
$\mathcal{O}_Y(U)[x_1,\dots,x_n]$.
Let R be a semiring, T be a multiplicative subset of R, and M be an R-module. As in the case for rings, one has the following isomorphism:
Now, the following lemma 3.4 and proposition 3.5 boil down to (7).
Lemma 3.4. Let ![]() $(X,f,\{U_i\},\{\psi_i\})$ be geometric vector bundles on a scheme Y over
$(X,f,\{U_i\},\{\psi_i\})$ be geometric vector bundles on a scheme Y over ![]() $\mathbb{N}$. Let
$\mathbb{N}$. Let ![]() $\{U_j'\}$ be another covering of Y. Let
$\{U_j'\}$ be another covering of Y. Let ![]() $U_{ij}:=U_i \cap U_j'$ and ψij be the restriction of ψi to
$U_{ij}:=U_i \cap U_j'$ and ψij be the restriction of ψi to ![]() $f^{-1}(U_{ij})$. Then,
$f^{-1}(U_{ij})$. Then, ![]() $(X,f,\{U_{ij}\},\{\psi_{ij}\}\}$ is a geometric vector bundle that is isomorphic to
$(X,f,\{U_{ij}\},\{\psi_{ij}\}\}$ is a geometric vector bundle that is isomorphic to ![]() $(X,f,\{U_i\},\{\psi_i\})$.
$(X,f,\{U_i\},\{\psi_i\})$.
Proof. To show that ![]() $(X,f,\{U_{ij}\},\{\psi_{ij}\}\}$ is a geometric vector bundle, it suffices to prove that
$(X,f,\{U_{ij}\},\{\psi_{ij}\}\}$ is a geometric vector bundle, it suffices to prove that  $\psi_{ij}:f^{-1}(U_{ij}) \to \mathbb{A}^n_{U_{ij}}$ is an isomorphism. In fact, we may further assume that
$\psi_{ij}:f^{-1}(U_{ij}) \to \mathbb{A}^n_{U_{ij}}$ is an isomorphism. In fact, we may further assume that ![]() $U_{i}=\operatorname{Spec} R_i$ and
$U_{i}=\operatorname{Spec} R_i$ and ![]() $U_{ij}=\operatorname{Spec} (R_i)_{f_j}$ for some
$U_{ij}=\operatorname{Spec} (R_i)_{f_j}$ for some ![]() $f_j \in R_i$. Then, it reduces to show that for a free Ri-module Mi,
$f_j \in R_i$. Then, it reduces to show that for a free Ri-module Mi,
which is true for modules over semirings.
Finally, it is clear that ![]() $(X,f,\{U_{ij}\},\{\psi_{ij}\}\}$ is isomorphic to
$(X,f,\{U_{ij}\},\{\psi_{ij}\}\}$ is isomorphic to ![]() $(X,f,\{U_i\},\{\psi_i\})$.
$(X,f,\{U_i\},\{\psi_i\})$.
Proposition 3.5. Let ![]() $\mathcal{F}$ be a locally free sheaf of rank n on a scheme Y over
$\mathcal{F}$ be a locally free sheaf of rank n on a scheme Y over ![]() $\mathbb{N}$ and
$\mathbb{N}$ and ![]() $X=\operatorname{Spec} (\text{Sym}(\mathcal{F}))$. With f and Ui as in (5),
$X=\operatorname{Spec} (\text{Sym}(\mathcal{F}))$. With f and Ui as in (5), ![]() $(X,f,\{U_i\},\{\psi_i\})$ is a geometric vector bundle of rank n over Y, which (up to isomorphism) does not depend on the basis of
$(X,f,\{U_i\},\{\psi_i\})$ is a geometric vector bundle of rank n over Y, which (up to isomorphism) does not depend on the basis of ![]() $\mathcal{F}|_{U_i}$ chosen.
$\mathcal{F}|_{U_i}$ chosen.
Proof. The proof follows mutatis mutandis as the one for schemes over rings.
Lemma 3.6. (Universal property of symmetric algebras) Let Y be a scheme and ![]() $\mathcal{F}$ be an
$\mathcal{F}$ be an ![]() $\mathcal{O}_Y$-module. Let
$\mathcal{O}_Y$-module. Let ![]() $i:\mathcal{F} \to \text{Sym}(\mathcal{F})$ be a natural map. For each sheaf
$i:\mathcal{F} \to \text{Sym}(\mathcal{F})$ be a natural map. For each sheaf ![]() $\mathcal{G}$ of
$\mathcal{G}$ of ![]() $\mathcal{O}_Y$-algebras and map
$\mathcal{O}_Y$-algebras and map ![]() $f:\mathcal{F} \to \mathcal{G}$ of
$f:\mathcal{F} \to \mathcal{G}$ of ![]() $\mathcal{O}_Y$-modules, there exists a unique map
$\mathcal{O}_Y$-modules, there exists a unique map ![]() $g:\text{Sym}(\mathcal{F}) \to \mathcal{G}$ of
$g:\text{Sym}(\mathcal{F}) \to \mathcal{G}$ of ![]() $\mathcal{O}_Y$-algebras such that
$\mathcal{O}_Y$-algebras such that ![]() $g=f\circ i$.
$g=f\circ i$.
Proof. The proof follows mutatis mutandis as the one for schemes over rings.
Let Y be a scheme. For ![]() $\mathcal{O}_Y$-modules
$\mathcal{O}_Y$-modules ![]() $\mathcal{F}$ and
$\mathcal{F}$ and ![]() $\mathcal{G}$, we let
$\mathcal{G}$, we let ![]() $\underline{\mathrm{Hom}}_{\mathcal{O}_Y}(\mathcal{F},\mathcal{G})$ be the sheaf: for each open
$\underline{\mathrm{Hom}}_{\mathcal{O}_Y}(\mathcal{F},\mathcal{G})$ be the sheaf: for each open ![]() $U \subseteq Y$
$U \subseteq Y$
Note that as in the case for rings, ![]() $\underline{\mathrm{Hom}}_{\mathcal{O}_Y}(\mathcal{F},\mathcal{G})$ is indeed a sheaf. We let
$\underline{\mathrm{Hom}}_{\mathcal{O}_Y}(\mathcal{F},\mathcal{G})$ is indeed a sheaf. We let ![]() $\mathrm{Hom}_{\mathcal{O}_Y}(\mathcal{F},\mathcal{G})$ be the monoid of maps of
$\mathrm{Hom}_{\mathcal{O}_Y}(\mathcal{F},\mathcal{G})$ be the monoid of maps of ![]() $\mathcal{O}_Y$-modules.
$\mathcal{O}_Y$-modules.
We will later need an explicit description of the functor of points of a tensor product of locally free sheaves. For this we will need the Hom-tensor adjunction.
Lemma 3.7. Let ![]() $(X, \mathcal{O}_X)$ be a semiringed space. Let
$(X, \mathcal{O}_X)$ be a semiringed space. Let ![]() $\mathcal{E}, \mathcal{F}, \mathcal{G}$ be
$\mathcal{E}, \mathcal{F}, \mathcal{G}$ be ![]() $\mathcal{O}_X$-modules. Then there is an isomorphism
$\mathcal{O}_X$-modules. Then there is an isomorphism
which is natural in all arguments, where ![]() $\underline{\mathrm{Hom}}$ is the sheaf-valued Hom.
$\underline{\mathrm{Hom}}$ is the sheaf-valued Hom.
Proof. The proof follows mutatis mutandis as the one for schemes over rings.
As in the case for rings, one also has the following.
Lemma 3.8. Let ![]() $f:X \to Y$ be a morphism of schemes over
$f:X \to Y$ be a morphism of schemes over ![]() $\mathbb{N}$. Let
$\mathbb{N}$. Let ![]() $\mathcal{F}$ (resp.
$\mathcal{F}$ (resp. ![]() $\mathcal{G}$) be an
$\mathcal{G}$) be an ![]() $\mathcal{O}_X$-module (resp.
$\mathcal{O}_X$-module (resp. ![]() $\mathcal{O}_Y$-module). Then one has the following pullback-pushforward adjunction:
$\mathcal{O}_Y$-module). Then one has the following pullback-pushforward adjunction:
Proof. The proof follows mutatis mutandis as the one for schemes over rings.
Proposition 3.9. Let Y be a scheme and ![]() $\mathcal{F}$ be a locally free
$\mathcal{F}$ be a locally free ![]() $\mathcal{O}_Y$-module of finite rank. The dual
$\mathcal{O}_Y$-module of finite rank. The dual ![]() $\mathcal{F}^\vee$ is defined to be the sheaf
$\mathcal{F}^\vee$ is defined to be the sheaf ![]() $\underline{\mathrm{Hom}}_{\mathcal{O}_Y}(\mathcal{F},\mathcal{O}_Y)$. Let
$\underline{\mathrm{Hom}}_{\mathcal{O}_Y}(\mathcal{F},\mathcal{O}_Y)$. Let ![]() $X=\mathbf{V}(\mathcal{F})$ be the geometric vector bundle over Y associated with
$X=\mathbf{V}(\mathcal{F})$ be the geometric vector bundle over Y associated with ![]() $\mathcal{F}$ with
$\mathcal{F}$ with ![]() $f:X \to Y$. Let
$f:X \to Y$. Let ![]() $\mathcal{E}$ be the locally free sheaf of sections of X. Then
$\mathcal{E}$ be the locally free sheaf of sections of X. Then ![]() $\mathcal{E}$ is isomorphic to
$\mathcal{E}$ is isomorphic to ![]() $\mathcal{F}^\vee$.
$\mathcal{F}^\vee$.
Proof. The proof follows mutatis mutandis as the one for schemes over rings.
From lemma 3.2 and propositions 3.5 and 3.9, one obtains the following.
Proposition 3.10. Let Y be a scheme over ![]() $\mathbb{N}$. Then there is a one-to-one correspondence between isomorphism classes of geometric vector bundles on Y and isomorphism classes of locally free sheaves on Y.
$\mathbb{N}$. Then there is a one-to-one correspondence between isomorphism classes of geometric vector bundles on Y and isomorphism classes of locally free sheaves on Y.
From the above proposition, over semirings, we may identify geometric vector bundles and locally free sheaves. In the following, we provide a description of a locally free sheaf as a functor of points. This perspective will be used in later sections. We start with the following lemma.
Lemma 3.11. Let ![]() $f: X\rightarrow Y$ be a morphism of schemes over
$f: X\rightarrow Y$ be a morphism of schemes over ![]() $\mathbb{N}$. Let
$\mathbb{N}$. Let ![]() $\pi: E\rightarrow Y$ be a geometric vector bundle. Then the pullback
$\pi: E\rightarrow Y$ be a geometric vector bundle. Then the pullback ![]() $p: E \times_Y X \rightarrow X$ of E along f is a geometric vector bundle.
$p: E \times_Y X \rightarrow X$ of E along f is a geometric vector bundle.
Proof. The proof follows mutatis mutandis as the one for schemes over rings.
Let Y be a scheme over a semiring R and ![]() $\pi:E \to Y$ be a geometric vector bundle. Let A be an R-algebra and
$\pi:E \to Y$ be a geometric vector bundle. Let A be an R-algebra and ![]() $Y(A)=\operatorname{Hom}_{R}(\operatorname{Spec} A, Y)$ and
$Y(A)=\operatorname{Hom}_{R}(\operatorname{Spec} A, Y)$ and ![]() $E(A)=\operatorname{Hom}_{R}(\operatorname{Spec} A, E)$. For each
$E(A)=\operatorname{Hom}_{R}(\operatorname{Spec} A, E)$. For each ![]() $y:\operatorname{Spec} A \to Y$ of Y(A), we let Ey be the pullback of the following diagram (taken in the category of sets):
$y:\operatorname{Spec} A \to Y$ of Y(A), we let Ey be the pullback of the following diagram (taken in the category of sets):

where ![]() $\tilde{\pi}(x)=\pi\circ x$.
$\tilde{\pi}(x)=\pi\circ x$.
For an R-algebra morphism ![]() $\phi:A \to B$ and the induced map
$\phi:A \to B$ and the induced map ![]() $\phi^*:\operatorname{Spec} B \to \operatorname{Spec} A$, we have
$\phi^*:\operatorname{Spec} B \to \operatorname{Spec} A$, we have
Proposition 3.12. With the same notation as above, the functor of points E(A) has the following properties:
(1) The pullback Ey is in canonical bijection with the set of global sections of the pullback bundle
 $p:E \times_Y \operatorname{Spec} A \to \operatorname{Spec} A$, where
$p:E \times_Y \operatorname{Spec} A \to \operatorname{Spec} A$, where  $\operatorname{Spec} A$ is viewed as a scheme over Y via y.
$\operatorname{Spec} A$ is viewed as a scheme over Y via y.(2) For an R-algebra morphism
 $\phi: A \rightarrow B$ and
$\phi: A \rightarrow B$ and  $y \in Y(A)$, the restriction of
$y \in Y(A)$, the restriction of  $\phi_*:E(A) \to E(B)$ to Ey is the map
$\phi_*:E(A) \to E(B)$ to Ey is the map
 \begin{equation*}
\phi_*: E_y \rightarrow E_{x}, \quad \textrm{where } x=y\circ \phi^*,
\end{equation*}
\begin{equation*}
\phi_*: E_y \rightarrow E_{x}, \quad \textrm{where } x=y\circ \phi^*,
\end{equation*}given by sending a section
 $s\in E_y$ (which may be viewed as a map
$s\in E_y$ (which may be viewed as a map  $\operatorname{Spec} A\rightarrow E \times_Y \operatorname{Spec} A$) to the pullback map
$\operatorname{Spec} A\rightarrow E \times_Y \operatorname{Spec} A$) to the pullback map  $\operatorname{Spec} B\rightarrow E \times_Y \operatorname{Spec} B$ viewed as an element of the fibre Ex.
$\operatorname{Spec} B\rightarrow E \times_Y \operatorname{Spec} B$ viewed as an element of the fibre Ex.
Proof. Let ![]() $y\in Y(A)$. Elements of Ey are morphisms
$y\in Y(A)$. Elements of Ey are morphisms ![]() $v: \operatorname{Spec} A\rightarrow E$ such that
$v: \operatorname{Spec} A\rightarrow E$ such that ![]() $\pi\circ v = y$. These are equivalent to pairs of morphisms
$\pi\circ v = y$. These are equivalent to pairs of morphisms ![]() $v: \operatorname{Spec} A\rightarrow E$ and
$v: \operatorname{Spec} A\rightarrow E$ and ![]() $u: \operatorname{Spec} A\rightarrow \operatorname{Spec} A$ such that u is the identity map and
$u: \operatorname{Spec} A\rightarrow \operatorname{Spec} A$ such that u is the identity map and ![]() $\pi\circ v = y \circ \mathrm{id}$. Without the condition that u is the identity, such pairs correspond to morphisms
$\pi\circ v = y \circ \mathrm{id}$. Without the condition that u is the identity, such pairs correspond to morphisms ![]() $\eta: \operatorname{Spec} A \rightarrow E\times_Y \operatorname{Spec} A$, so with this condition included, such pairs correspond to morphisms
$\eta: \operatorname{Spec} A \rightarrow E\times_Y \operatorname{Spec} A$, so with this condition included, such pairs correspond to morphisms ![]() $\eta: \operatorname{Spec} A \rightarrow E\times_Y \operatorname{Spec} A$ whose composition with the projection
$\eta: \operatorname{Spec} A \rightarrow E\times_Y \operatorname{Spec} A$ whose composition with the projection ![]() $p: E\times_Y \operatorname{Spec} A \rightarrow \operatorname{Spec} A$ is the identity. These are the same as global sections of the sheaf associated with the pullback bundle
$p: E\times_Y \operatorname{Spec} A \rightarrow \operatorname{Spec} A$ is the identity. These are the same as global sections of the sheaf associated with the pullback bundle ![]() $p: E\times_Y \operatorname{Spec} A \rightarrow \operatorname{Spec} A$. This establishes the first claim.
$p: E\times_Y \operatorname{Spec} A \rightarrow \operatorname{Spec} A$. This establishes the first claim.
Let ![]() $v\in E_y$. We identify v with the map
$v\in E_y$. We identify v with the map ![]() $s: \operatorname{Spec} A\rightarrow E \times_Y \operatorname{Spec} A$ obtained by applying the universal property of the pullback to v and
$s: \operatorname{Spec} A\rightarrow E \times_Y \operatorname{Spec} A$ obtained by applying the universal property of the pullback to v and ![]() $\mathrm{id}$. By applying
$\mathrm{id}$. By applying ![]() $- \times_{\operatorname{Spec} A} \operatorname{Spec} B$ we obtain a map
$- \times_{\operatorname{Spec} A} \operatorname{Spec} B$ we obtain a map ![]() $t: \operatorname{Spec} B\rightarrow E \times_Y \operatorname{Spec} B$. So, we have the following diagram:
$t: \operatorname{Spec} B\rightarrow E \times_Y \operatorname{Spec} B$. So, we have the following diagram:

Since all squares are pullback squares, one can easily see that t is the global section corresponding to the element ![]() $\phi_*(v)=v\circ \phi^*$.
$\phi_*(v)=v\circ \phi^*$.
Proposition 3.12 motivates our definition of the functor of points of a locally free sheaf, which will be given shortly. But first we need to define the pullback of a global section of a sheaf.
Remark 3.13. Let ![]() $f: Y\rightarrow X$ be a morphism of schemes over
$f: Y\rightarrow X$ be a morphism of schemes over ![]() $\mathbb{N}$ and
$\mathbb{N}$ and ![]() $\mathcal{F}$ be an
$\mathcal{F}$ be an ![]() $\mathcal{O}_X$-module. Then any global section
$\mathcal{O}_X$-module. Then any global section ![]() $s\in \Gamma(X, \mathcal{F})$ induces a global section of
$s\in \Gamma(X, \mathcal{F})$ induces a global section of ![]() $f^*\mathcal{F}$ by functoriality of pullbacks: Specifying the global section s is equivalent to specifying a morphism
$f^*\mathcal{F}$ by functoriality of pullbacks: Specifying the global section s is equivalent to specifying a morphism ![]() $\mathcal{O}_X\rightarrow \mathcal{F}$, which may be pulled back to a morphism
$\mathcal{O}_X\rightarrow \mathcal{F}$, which may be pulled back to a morphism ![]() $\mathcal{O}_Y = f^*\mathcal{O}_X \rightarrow f^*\mathcal{F}$.
$\mathcal{O}_Y = f^*\mathcal{O}_X \rightarrow f^*\mathcal{F}$.
Let ![]() $\mathcal{F}$ be a locally free sheaf on a scheme X over a semiring R. For an R-algebra A and a morphism
$\mathcal{F}$ be a locally free sheaf on a scheme X over a semiring R. For an R-algebra A and a morphism ![]() $x: \operatorname{Spec} A\rightarrow X$, the fibre
$x: \operatorname{Spec} A\rightarrow X$, the fibre ![]() $\mathcal{F}_x$ is defined as the global sections of the pullback sheaf
$\mathcal{F}_x$ is defined as the global sections of the pullback sheaf ![]() $x^*\mathcal{F}$, i.e.,
$x^*\mathcal{F}$, i.e.,
The set ![]() $\mathcal{F}(A)$ of A-valued points is defined as the union of
$\mathcal{F}(A)$ of A-valued points is defined as the union of ![]() $\mathcal{F}_x$ over all
$\mathcal{F}_x$ over all ![]() $x\in X(A)$.
$x\in X(A)$.
Given an R-algebra morphism ![]() $f: A\rightarrow B$ and an element
$f: A\rightarrow B$ and an element ![]() $v\in \mathcal{F}_x$ of some fibre, let
$v\in \mathcal{F}_x$ of some fibre, let ![]() $f^*(v) \in \mathcal{F}_{f^*(x)}$ as the pullback of the global section v along
$f^*(v) \in \mathcal{F}_{f^*(x)}$ as the pullback of the global section v along ![]() $f^*:\operatorname{Spec} B \to \operatorname{Spec} A$ as explained in remark 3.13. Now, the functor of points of
$f^*:\operatorname{Spec} B \to \operatorname{Spec} A$ as explained in remark 3.13. Now, the functor of points of ![]() $\mathcal{F}$ is defined as follows.
$\mathcal{F}$ is defined as follows.
Definition 3.14. Let ![]() $\mathcal{F}$ be a locally free sheaf on a scheme X over a semiring R. The functor of points of
$\mathcal{F}$ be a locally free sheaf on a scheme X over a semiring R. The functor of points of ![]() $\mathcal{F}$ is the functor sending an R-algebra A to
$\mathcal{F}$ is the functor sending an R-algebra A to ![]() $\mathcal{F}(A)$ and an R-algebra morphism
$\mathcal{F}(A)$ and an R-algebra morphism ![]() $f:A\rightarrow B$ to the morphism
$f:A\rightarrow B$ to the morphism ![]() $\mathcal{F}(A)\rightarrow\mathcal{F}(B)$ given by
$\mathcal{F}(A)\rightarrow\mathcal{F}(B)$ given by ![]() $v\mapsto f^*(v)$.
$v\mapsto f^*(v)$.
We show that the functor of points of a locally free sheaf is equal to the functor of points of the corresponding geometric vector bundle. The only difficulty is that the definition of the functor of points of a locally free sheaf involves the pullback sheaf rather than the sheaf corresponding to the pullback of the geometric vector bundle.
Lemma 3.15. Let ![]() $\pi: E\rightarrow X$ be a geometric vector bundle, and let
$\pi: E\rightarrow X$ be a geometric vector bundle, and let ![]() $f:Y\rightarrow X$ be a morphism of schemes. Let
$f:Y\rightarrow X$ be a morphism of schemes. Let ![]() $\mathcal{F}$ be the sheaf of sections of E. Then the sheaf
$\mathcal{F}$ be the sheaf of sections of E. Then the sheaf ![]() $\mathcal{G}$ of sections of
$\mathcal{G}$ of sections of ![]() $E\times_X Y\rightarrow Y$ is canonically isomorphic to
$E\times_X Y\rightarrow Y$ is canonically isomorphic to ![]() $f^*\mathcal{F}$.
$f^*\mathcal{F}$.
Proof. Let ![]() $U\subseteq X$ be an open subset. A section of E over U may be pulled back to a section of
$U\subseteq X$ be an open subset. A section of E over U may be pulled back to a section of ![]() $E\times_X Y$ over
$E\times_X Y$ over ![]() $f^{-1}(U)$. Since
$f^{-1}(U)$. Since ![]() $f_*\mathcal{G}$ sends U to the sections of
$f_*\mathcal{G}$ sends U to the sections of ![]() $E\times_X Y$ over
$E\times_X Y$ over ![]() $f^{-1}(U)$, we have obtained a homomorphism
$f^{-1}(U)$, we have obtained a homomorphism ![]() $\mathcal{F}\rightarrow f_*\mathcal{G}$. By adjunction we obtain a homomorphism
$\mathcal{F}\rightarrow f_*\mathcal{G}$. By adjunction we obtain a homomorphism ![]() $f^*\mathcal{F}\rightarrow \mathcal{G}$.
$f^*\mathcal{F}\rightarrow \mathcal{G}$.
To check this is an isomorphism, we may work locally (or even on stalks), and so we may assume E is the trivial bundle. Choose a basis ![]() $v_1,\ldots, v_n$ of sections of E, and equip
$v_1,\ldots, v_n$ of sections of E, and equip ![]() $E\times_X Y$ with the pulled back basis
$E\times_X Y$ with the pulled back basis ![]() $w_1, \ldots, w_n$. We may now identify
$w_1, \ldots, w_n$. We may now identify ![]() $\mathcal{F}$ with
$\mathcal{F}$ with ![]() $\mathcal{O}_X^n$ and
$\mathcal{O}_X^n$ and ![]() $\mathcal{G}$ with
$\mathcal{G}$ with ![]() $\mathcal{O}_Y^n$. The map
$\mathcal{O}_Y^n$. The map ![]() $\mathcal{F}\rightarrow f_*\mathcal{G}$ we constructed above is the map
$\mathcal{F}\rightarrow f_*\mathcal{G}$ we constructed above is the map ![]() $\mathcal{O}_X^n \rightarrow f_*\mathcal{O}_Y^n$ sending one basis to the other (i.e., the direct sum of many copies of the canonical map
$\mathcal{O}_X^n \rightarrow f_*\mathcal{O}_Y^n$ sending one basis to the other (i.e., the direct sum of many copies of the canonical map ![]() $\mathcal{O}_X\rightarrow f_*\mathcal{O}_Y$. The map
$\mathcal{O}_X\rightarrow f_*\mathcal{O}_Y$. The map ![]() $f^*\mathcal{F}\rightarrow \mathcal{G}$ is then the map
$f^*\mathcal{F}\rightarrow \mathcal{G}$ is then the map ![]() $f^*\mathcal{O}_X^n\rightarrow \mathcal{O}_Y^n$ obtained as the direct sum of copies of the canonical isomorphism
$f^*\mathcal{O}_X^n\rightarrow \mathcal{O}_Y^n$ obtained as the direct sum of copies of the canonical isomorphism ![]() $f^*\mathcal{O}_X\rightarrow \mathcal{O}_Y$.
$f^*\mathcal{O}_X\rightarrow \mathcal{O}_Y$.
Note that proposition 3.12 looks almost identical to the definition of the functor of points of a locally free sheaf in definition 3.14; the only major difference is that it involves pullbacks of schemes instead of pullbacks of sheaves, which is shown to be equivalent by lemma 3.15. To be precise, we have following.
Corollary 3.16. The functor of points of a geometric vector bundle is the same as that of the corresponding locally free sheaf.
Proof. First, we consider what the functor of points looks like on objects via the first statement of proposition 3.12.
Let R be a semiring and A be an R-algebra. For any geometric vector bundle E on a scheme Y over R, the set E(A) is the disjoint union of Ey over all ![]() $ y \in Y(A)$. Also, for each
$ y \in Y(A)$. Also, for each ![]() $y \in Y(A)$, proposition 3.12 says that Ey is the set of global sections of the pullback of E along y.
$y \in Y(A)$, proposition 3.12 says that Ey is the set of global sections of the pullback of E along y.
Moreover, from lemma 3.15, we know that the sections of this pullback bundle are just global sections of the pullback sheaf. It follows that Ey is the set of global sections of ![]() $y^*\mathcal{F}$ where
$y^*\mathcal{F}$ where ![]() $\mathcal{F}$ is the sheaf of sections of E. By the definition of the functor of points of a locally free sheaf, we can write this as
$\mathcal{F}$ is the sheaf of sections of E. By the definition of the functor of points of a locally free sheaf, we can write this as ![]() $E_y = \mathcal{F}_y$. Then taking the union over all
$E_y = \mathcal{F}_y$. Then taking the union over all ![]() $y \in Y(A)$ gives
$y \in Y(A)$ gives
The case of morphisms is followed by a similar argument.
Because the functor of points is defined in terms of the pullback sheaf, it will be useful to understand the pullback of a tensor product. For this, the following lemma will be helpful.
Lemma 3.17. Let ![]() $f:X\rightarrow Y$ be a morphism of schemes over
$f:X\rightarrow Y$ be a morphism of schemes over ![]() $\mathbb{N}$. Let
$\mathbb{N}$. Let ![]() $U\subseteq Y$ be an open subset.
$U\subseteq Y$ be an open subset.
(1) Let
 $\mathcal{F}$ be an
$\mathcal{F}$ be an  $\mathcal{O}_Y$-module and
$\mathcal{O}_Y$-module and  $\mathcal{G}$ be a module over
$\mathcal{G}$ be a module over  $\mathcal{O}_Y\mid_U$. Define
$\mathcal{O}_Y\mid_U$. Define  $\mathcal{H}$ on Y by
$\mathcal{H}$ on Y by  $\mathcal{H}(V) = \mathcal{G}(U\cap V)$. Then
$\mathcal{H}(V) = \mathcal{G}(U\cap V)$. Then  $\operatorname{Hom}_{\mathcal{O}_Y\mid_U}(\mathcal{F}\mid_U, \mathcal{G}) \cong \operatorname{Hom}_{\mathcal{O}_Y}(\mathcal{F}, \mathcal{H})$.
$\operatorname{Hom}_{\mathcal{O}_Y\mid_U}(\mathcal{F}\mid_U, \mathcal{G}) \cong \operatorname{Hom}_{\mathcal{O}_Y}(\mathcal{F}, \mathcal{H})$.(2) Let
 $\mathcal{F}$ be an
$\mathcal{F}$ be an  $\mathcal{O}_X$-module. Let
$\mathcal{O}_X$-module. Let  $j: f^{-1}(U)\rightarrow X$ be the inclusion. Then
$j: f^{-1}(U)\rightarrow X$ be the inclusion. Then  $f_*j_*(\mathcal{F}\mid_{f^{-1}(U)})$ sends an open subset
$f_*j_*(\mathcal{F}\mid_{f^{-1}(U)})$ sends an open subset  $V\subseteq X$ to
$V\subseteq X$ to  $(f_*\mathcal{F})(U\cap V)$.
$(f_*\mathcal{F})(U\cap V)$.(3) Let
 $\mathcal{F}$ be an
$\mathcal{F}$ be an  $\mathcal{O}_Y$-module and
$\mathcal{O}_Y$-module and  $\mathcal{G}$ be an
$\mathcal{G}$ be an  $\mathcal{O}_X$-module. There is a natural isomorphism
(9)
$\mathcal{O}_X$-module. There is a natural isomorphism
(9) \begin{equation}
\underline{\operatorname{Hom}}_{\mathcal{O}_Y}(\mathcal{F}, f_*\mathcal{G}) \cong f_*\underline{\operatorname{Hom}}_{\mathcal{O}_X}(f^*\mathcal{F}, \mathcal{G}).
\end{equation}
\begin{equation}
\underline{\operatorname{Hom}}_{\mathcal{O}_Y}(\mathcal{F}, f_*\mathcal{G}) \cong f_*\underline{\operatorname{Hom}}_{\mathcal{O}_X}(f^*\mathcal{F}, \mathcal{G}).
\end{equation}
Proof. The proof follows mutatis mutandis as the one for schemes over rings.
Lemma 3.18. Let ![]() $f:X\rightarrow Y$ be a morphism of schemes over
$f:X\rightarrow Y$ be a morphism of schemes over ![]() $\mathbb{N}$. Let
$\mathbb{N}$. Let ![]() $\mathcal{F}, \mathcal{G}$ be locally free sheaves on Y. Then there is a natural isomorphism
$\mathcal{F}, \mathcal{G}$ be locally free sheaves on Y. Then there is a natural isomorphism ![]() $f^*(\mathcal{F})\otimes_{\mathcal{O}_X} f^*(\mathcal{G})\rightarrow f^*(\mathcal{F}\otimes_{\mathcal{O}_Y} \mathcal{G})$.
$f^*(\mathcal{F})\otimes_{\mathcal{O}_X} f^*(\mathcal{G})\rightarrow f^*(\mathcal{F}\otimes_{\mathcal{O}_Y} \mathcal{G})$.
Proof. Let ![]() $\mathcal{H}$ be a sheaf on X. Then by the hom-tensor adjunction and the pullback-pushforward adjunction, we obtain
$\mathcal{H}$ be a sheaf on X. Then by the hom-tensor adjunction and the pullback-pushforward adjunction, we obtain
and
The result follows by using (9) (with ![]() $\mathcal{G}, \mathcal{H}$ in place of
$\mathcal{G}, \mathcal{H}$ in place of ![]() $\mathcal{F}, \mathcal{G}$) to compare the right sides of the two equations above.
$\mathcal{F}, \mathcal{G}$) to compare the right sides of the two equations above.
Proposition 3.19. Let X be a scheme over a semiring R and ![]() $\mathcal{F}, \mathcal{G}$ be locally free sheaves on X. The functor of points of
$\mathcal{F}, \mathcal{G}$ be locally free sheaves on X. The functor of points of ![]() $\mathcal{F}\otimes_{\mathcal{O}_X}\mathcal{G}$ is given by
$\mathcal{F}\otimes_{\mathcal{O}_X}\mathcal{G}$ is given by  $A\mapsto \bigsqcup_{x\in X(A)}\mathcal{F}_x\otimes_{A}\mathcal{G}_x$.
$A\mapsto \bigsqcup_{x\in X(A)}\mathcal{F}_x\otimes_{A}\mathcal{G}_x$.
Proof. This is just a restatement of lemma 3.18. Let A be an R-algebra and let ![]() $x\in X(A)$. Then by definition, the fibre of
$x\in X(A)$. Then by definition, the fibre of ![]() $(\mathcal{F}\otimes_{\mathcal{O}_X}\mathcal{G})(A)\rightarrow X(A)$ over x is the A-module corresponding to
$(\mathcal{F}\otimes_{\mathcal{O}_X}\mathcal{G})(A)\rightarrow X(A)$ over x is the A-module corresponding to ![]() $x^*(\mathcal{F}\otimes_{\mathcal{O}_X}\mathcal{G})$, which is isomorphic to
$x^*(\mathcal{F}\otimes_{\mathcal{O}_X}\mathcal{G})$, which is isomorphic to ![]() $x^*(\mathcal{F})\otimes_A x^*(\mathcal{G})$. This is the tensor product of the fibres of
$x^*(\mathcal{F})\otimes_A x^*(\mathcal{G})$. This is the tensor product of the fibres of ![]() $\mathcal{F}$ and
$\mathcal{F}$ and ![]() $\mathcal{G}$.
$\mathcal{G}$.
Proposition 3.20. Let E be a locally free sheaf on a scheme X over a semiring R. Consider the map ![]() $+:E\times_X E \to E$ which is simply vector addition on the level of functors of points. Then, + is a morphism of schemes when E is viewed as a geometric vector bundle. Similarly, there is a morphism of schemes
$+:E\times_X E \to E$ which is simply vector addition on the level of functors of points. Then, + is a morphism of schemes when E is viewed as a geometric vector bundle. Similarly, there is a morphism of schemes ![]() $\mathbb{A}^1_X \times_XE \to E$ whose functor of points is the scalar multiplication map
$\mathbb{A}^1_X \times_XE \to E$ whose functor of points is the scalar multiplication map ![]() $(A \times X(A))\times_{X(A)} E(A) \cong A \times E(A) \to E(A)$.
$(A \times X(A))\times_{X(A)} E(A) \cong A \times E(A) \to E(A)$.
Proof. Since the fibres are A-modules, we have an addition operation
which is natural in A because pulling back sections yields an additive map ![]() $E(A)\rightarrow E(B)$ for any
$E(A)\rightarrow E(B)$ for any ![]() $f: A\rightarrow B$. The universal property of pullback yields a natural isomorphism
$f: A\rightarrow B$. The universal property of pullback yields a natural isomorphism
Composing gives a natural addition operation ![]() $(E\times_X E)(A) \rightarrow E(A)$. By naturality, this must be the functor of points of a morphism of schemes.
$(E\times_X E)(A) \rightarrow E(A)$. By naturality, this must be the functor of points of a morphism of schemes.
The proof for scalar multiplication is similar; the only substantial difference is that we need to check that ![]() $A \times E(A)\rightarrow E(A)$ is natural. If
$A \times E(A)\rightarrow E(A)$ is natural. If ![]() $x\in X(A)$ and
$x\in X(A)$ and ![]() $f:A\rightarrow B$, this amounts to showing that the composition of
$f:A\rightarrow B$, this amounts to showing that the composition of ![]() $A\times E_x \rightarrow E_x$ with the map
$A\times E_x \rightarrow E_x$ with the map ![]() $E_x \rightarrow E_{f(x)} \cong E_x \otimes_A B$ (given by
$E_x \rightarrow E_{f(x)} \cong E_x \otimes_A B$ (given by ![]() $v\mapsto v\otimes 1$) is equal to the composition of the map
$v\mapsto v\otimes 1$) is equal to the composition of the map ![]() $A\times E_x \rightarrow B \times E_{f(x)}$ (given by
$A\times E_x \rightarrow B \times E_{f(x)}$ (given by ![]() $a,v \mapsto f(a), v\otimes 1$) with
$a,v \mapsto f(a), v\otimes 1$) with ![]() $B \times E_{f(x)}\rightarrow E_{f(x)}$, which is clear.
$B \times E_{f(x)}\rightarrow E_{f(x)}$, which is clear.
4. Equivariant vector bundles
From now on, by a vector bundle, we mean a locally free sheaf.
Let E be a vector bundle on a scheme X over a semiring R. Let A be an R-algebra. Consider any element of X(A):
As we noted in remark 3.13, any global section s of E determines a global section of the pullback bundle ![]() $x^*E$. Since
$x^*E$. Since ![]() $E_x:=x^*(E)(\operatorname{Spec} A)$, the element s determines an element s(x) of Ex. Hence, s also determines a section of the projection
$E_x:=x^*(E)(\operatorname{Spec} A)$, the element s determines an element s(x) of Ex. Hence, s also determines a section of the projection ![]() $\pi_A:E(A) \to X(A)$.
$\pi_A:E(A) \to X(A)$.
Let R be a semiring. By a group scheme over R, we mean a group object in the category of schemes over R. In particular, for any R-algebra A, the set G(A) of A-points of G is a group. Also, recall that for any vector bundle E on X and ![]() $x \in X(A)$, since
$x \in X(A)$, since ![]() $E_x:=x^*E(\operatorname{Spec} A)$, the set Ex is indeed an A-module.
$E_x:=x^*E(\operatorname{Spec} A)$, the set Ex is indeed an A-module.
Definition 4.1. Let X be a scheme over a semiring R and G be a group scheme over R acting on X. We define an equivariant vector bundle to be a vector bundle E on X together with an action of G(A) on E(A) for each R-algebra A satisfying the following:
(1) the action is natural in A,
(2) the action makes πA equivariant, and
(3) the action makes the induced map
 $E_x \to E_{gx}$ A-linear.
$E_x \to E_{gx}$ A-linear.
The first condition means the following: for R-algebras A and B with a map ![]() $f^*:\operatorname{Spec} B \to \operatorname{Spec} A$ induced by an R-algebra map
$f^*:\operatorname{Spec} B \to \operatorname{Spec} A$ induced by an R-algebra map ![]() $f:A \to B$, the following diagram commutes:
$f:A \to B$, the following diagram commutes:

where ![]() $\varphi(\alpha)=\alpha \circ f^*$ and
$\varphi(\alpha)=\alpha \circ f^*$ and ![]() $\psi(\beta)=f^*(\beta)$ (as in definition 3.14) and ρA (resp. ρB) is an action of G(A) (resp. G(B)) on E(A) (resp. E(B)).
$\psi(\beta)=f^*(\beta)$ (as in definition 3.14) and ρA (resp. ρB) is an action of G(A) (resp. G(B)) on E(A) (resp. E(B)).
The second condition means that the following diagram commutes:

where the top row is the action of G(A) on E(A) and the bottom row is the action of G(A) on X(A).
The third condition is clear: each ![]() $g \in X(A)$ induces an automorphism of E(A) and it has to be A-linear for each fibre.
$g \in X(A)$ induces an automorphism of E(A) and it has to be A-linear for each fibre.
Example 4.2. Let X be a scheme over a semiring R with a G-action, where G is a group scheme over R. Consider a free sheaf ![]() $\mathcal{F} = \mathcal{O}_X^n$. Let
$\mathcal{F} = \mathcal{O}_X^n$. Let ![]() $v_1, \ldots, v_n$ be a basis for
$v_1, \ldots, v_n$ be a basis for ![]() $\mathcal{F}$. Let
$\mathcal{F}$. Let ![]() $x\in X(A)$ for some R-algebra A. Then
$x\in X(A)$ for some R-algebra A. Then ![]() $\mathcal{F}_x$ is free with basis
$\mathcal{F}_x$ is free with basis ![]() $(v_1)_x, \ldots, (v_n)_x$ where
$(v_1)_x, \ldots, (v_n)_x$ where ![]() $(v_i)_x\in \mathcal{F}_x$ corresponds to
$(v_i)_x\in \mathcal{F}_x$ corresponds to ![]() $x^*v_i\in \Gamma(\operatorname{Spec} A, x^*\mathcal{F})$.
$x^*v_i\in \Gamma(\operatorname{Spec} A, x^*\mathcal{F})$.
Define an action ![]() $\rho_A: G(A)\times \mathcal{F}(A)\rightarrow \mathcal{F}(A)$ by the condition that for
$\rho_A: G(A)\times \mathcal{F}(A)\rightarrow \mathcal{F}(A)$ by the condition that for ![]() $g\in G(A)$,
$g\in G(A)$, ![]() $x\in X(A)$ and
$x\in X(A)$ and ![]() $v\in \mathcal{F}_x$,
$v\in \mathcal{F}_x$,
 \begin{equation*}
\rho_A((g,v)) = \sum_i a_i (v_i)_{gx},
\end{equation*}
\begin{equation*}
\rho_A((g,v)) = \sum_i a_i (v_i)_{gx},
\end{equation*} where ![]() $v = \sum_i a_i (v_i)_x$ is the basis expansion of v.
$v = \sum_i a_i (v_i)_x$ is the basis expansion of v. ![]() $\mathcal{O}_X^n$ with this action is called the trivial G-equivariant vector bundle. It is clear that ρA is compatible with the projection since it maps the fibre over x to the fibre over gx. It is also clear that ρA is an action and that it induces linear isomorphisms between fibres. To show the trivial G-equivariant vector bundle is in fact an equivariant vector bundle, we only need to check naturality.
$\mathcal{O}_X^n$ with this action is called the trivial G-equivariant vector bundle. It is clear that ρA is compatible with the projection since it maps the fibre over x to the fibre over gx. It is also clear that ρA is an action and that it induces linear isomorphisms between fibres. To show the trivial G-equivariant vector bundle is in fact an equivariant vector bundle, we only need to check naturality.
Let ![]() $f^*:\operatorname{Spec} B \to \operatorname{Spec} A$ be a map induced by a map
$f^*:\operatorname{Spec} B \to \operatorname{Spec} A$ be a map induced by a map ![]() $f:A \to B$ of R-algebras. We want the following diagram to commute:
$f:A \to B$ of R-algebras. We want the following diagram to commute:

For ![]() $(g,v) \in G(A) \times \mathcal{F}(A)$, we have
$(g,v) \in G(A) \times \mathcal{F}(A)$, we have
 \begin{equation*}
\psi\circ\rho_A((g,v))=\psi(\sum_i a_i (v_i)_{gx})= \sum_i f(a_i) \psi((v_i)_{gx}) = \sum_i f(a_i) (f^*v_i)_{f^*(gx)}.
\end{equation*}
\begin{equation*}
\psi\circ\rho_A((g,v))=\psi(\sum_i a_i (v_i)_{gx})= \sum_i f(a_i) \psi((v_i)_{gx}) = \sum_i f(a_i) (f^*v_i)_{f^*(gx)}.
\end{equation*} On the other hand, with ![]() $v=\sum_i a_i(v_i)_x$, we have
$v=\sum_i a_i(v_i)_x$, we have
 \begin{equation*}
\psi(v)=\psi(\sum_ia_i(v_i)_x) = \sum_i f(a_i) \psi((v_i)_x) = \sum_i f(a_i)f^*((v_i)_x).
\end{equation*}
\begin{equation*}
\psi(v)=\psi(\sum_ia_i(v_i)_x) = \sum_i f(a_i) \psi((v_i)_x) = \sum_i f(a_i)f^*((v_i)_x).
\end{equation*}Hence, we have
 \begin{align*}
\rho_B\circ (\varphi \times \psi)(g,v)&= \rho_B(f^*(g), \sum_i f(a_i)(f^*v_i)_{f^*x}))=\sum_i f(a_i) (f^*v_i)_{f^*(g)f^*x}\\
&=\sum_i f(a_i)(f^*v_i)_{f^*(gx)},
\end{align*}
\begin{align*}
\rho_B\circ (\varphi \times \psi)(g,v)&= \rho_B(f^*(g), \sum_i f(a_i)(f^*v_i)_{f^*x}))=\sum_i f(a_i) (f^*v_i)_{f^*(g)f^*x}\\
&=\sum_i f(a_i)(f^*v_i)_{f^*(gx)},
\end{align*} showing that ![]() $\psi\circ \rho_A = \rho_B\circ (\varphi \times \psi)$.
$\psi\circ \rho_A = \rho_B\circ (\varphi \times \psi)$.
Obviously, a direct sum of equivariant vector bundles is an equivariant vector bundle. We now show that the same is true for tensor products.
Lemma 4.2. Let ![]() $f: Y\rightarrow X$ be a morphism of schemes over a semiring R and let
$f: Y\rightarrow X$ be a morphism of schemes over a semiring R and let ![]() $\mathcal{F}$ be a locally free sheaf on X. Then there is a canonical isomorphism
$\mathcal{F}$ be a locally free sheaf on X. Then there is a canonical isomorphism ![]() $f^*\underline{\operatorname{Hom}}_{\mathcal{O}_X}(\mathcal{F}, \mathcal{O}_X) \simeq \underline{\operatorname{Hom}}_{\mathcal{O}_Y}(f^*\mathcal{F}, \mathcal{O}_Y)$.
$f^*\underline{\operatorname{Hom}}_{\mathcal{O}_X}(\mathcal{F}, \mathcal{O}_X) \simeq \underline{\operatorname{Hom}}_{\mathcal{O}_Y}(f^*\mathcal{F}, \mathcal{O}_Y)$.
Proof. The proof follows mutatis mutandis as the one for schemes over rings.
Let X be a scheme over a semiring R with an action of a group scheme G over R. Let ![]() $\mathcal{E},\mathcal{F}$ be equivariant vector bundles on X. Let A be an R-algebra. We apply proposition 3.19 to identify
$\mathcal{E},\mathcal{F}$ be equivariant vector bundles on X. Let A be an R-algebra. We apply proposition 3.19 to identify ![]() $(\mathcal{E}\otimes\mathcal{F})_x$ with
$(\mathcal{E}\otimes\mathcal{F})_x$ with ![]() $\mathcal{E}_x \otimes_A \mathcal{F}_x$ for each
$\mathcal{E}_x \otimes_A \mathcal{F}_x$ for each ![]() $x\in X(A)$.
$x\in X(A)$.
Proposition 4.3. With the same notation as above, ![]() $\mathcal{E}\otimes\mathcal{F}$ is an equivariant vector bundle via the action obtained by linearly extending the following:
$\mathcal{E}\otimes\mathcal{F}$ is an equivariant vector bundle via the action obtained by linearly extending the following:
Moreover, the set of isomorphism classes of equivariant line bundles is a group under tensor product.
Proof. If ![]() $v\otimes w$ is in the fibre over x, then it is clear that
$v\otimes w$ is in the fibre over x, then it is clear that ![]() $gv\otimes gw$ is in the fibre over gx, which establishes compatibility with the projections, showing (2) of definition 4.1.
$gv\otimes gw$ is in the fibre over gx, which establishes compatibility with the projections, showing (2) of definition 4.1.
The linearity of the actions on ![]() $\mathcal{E}_x$ and
$\mathcal{E}_x$ and ![]() $\mathcal{F}_x$ implies
$\mathcal{F}_x$ implies ![]() $gv\otimes gw$ depends bilinearly on v and w. By the universal property of the tensor product, there is a unique linear map
$gv\otimes gw$ depends bilinearly on v and w. By the universal property of the tensor product, there is a unique linear map ![]() $\mathcal{E}_x \otimes \mathcal{F}_x \rightarrow \mathcal{E}_{gx} \otimes \mathcal{F}_{gx} $ sending
$\mathcal{E}_x \otimes \mathcal{F}_x \rightarrow \mathcal{E}_{gx} \otimes \mathcal{F}_{gx} $ sending ![]() $v\otimes w$ to
$v\otimes w$ to ![]() $gv\otimes gw$. This establishes that the map of interest is well-defined and linear on fibres. This shows (3) of definition 4.1.
$gv\otimes gw$. This establishes that the map of interest is well-defined and linear on fibres. This shows (3) of definition 4.1.
One can easily observe that (1) of definition 4.1 follows immediately from the naturality of the actions on ![]() $\mathcal{E}$ and
$\mathcal{E}$ and ![]() $\mathcal{F}$ plus naturality of the multiplication map
$\mathcal{F}$ plus naturality of the multiplication map ![]() $G(A)\times G(A)\rightarrow G(A)$. Thus the tensor product is an equivariant vector bundle.
$G(A)\times G(A)\rightarrow G(A)$. Thus the tensor product is an equivariant vector bundle.
Now let ![]() $\mathcal{O}_X$ be the trivial equivariant line bundle (with the basis element denoted 1). We have an isomorphism of vector bundles
$\mathcal{O}_X$ be the trivial equivariant line bundle (with the basis element denoted 1). We have an isomorphism of vector bundles
which on the level of functors of points is given by ![]() $1_x \otimes v \mapsto v$. To check if it is an isomorphism of G-equivariant vector bundles (so that
$1_x \otimes v \mapsto v$. To check if it is an isomorphism of G-equivariant vector bundles (so that ![]() $\mathcal{O}_X$ is the tensor product identity), we need to check that
$\mathcal{O}_X$ is the tensor product identity), we need to check that ![]() $g(1_x \otimes v)$ maps to gv. But this follows immediately from
$g(1_x \otimes v)$ maps to gv. But this follows immediately from ![]() $g(1_x \otimes v) = g1_x \otimes gv = 1_{gx} \otimes gv$.
$g(1_x \otimes v) = g1_x \otimes gv = 1_{gx} \otimes gv$.
It remains to show that equivariant line bundles are invertible under tensor product. Let L be an equivariant line bundle. There is a canonical morphism ![]() $\underline{\operatorname{Hom}}_{\mathcal{O}_X}(L, \mathcal{O}_X) \otimes L \rightarrow \mathcal{O}_X$. This is clearly an isomorphism for
$\underline{\operatorname{Hom}}_{\mathcal{O}_X}(L, \mathcal{O}_X) \otimes L \rightarrow \mathcal{O}_X$. This is clearly an isomorphism for ![]() $L = \mathcal{O}_X$, and so for any line bundle it induces isomorphisms on stalks, and hence is an isomorphism.
$L = \mathcal{O}_X$, and so for any line bundle it induces isomorphisms on stalks, and hence is an isomorphism.
By lemma 4.2, the functor of points of ![]() $\underline{\operatorname{Hom}}_{\mathcal{O}_X}(L, \mathcal{O}_X)$ has fibre over a point
$\underline{\operatorname{Hom}}_{\mathcal{O}_X}(L, \mathcal{O}_X)$ has fibre over a point ![]() $x\in X(A)$ given by
$x\in X(A)$ given by ![]() $\operatorname{Hom}_A(L_x, A)$. We may then define the action by saying
$\operatorname{Hom}_A(L_x, A)$. We may then define the action by saying ![]() $g\in G(A)$ acts on
$g\in G(A)$ acts on ![]() $\ell\in \operatorname{Hom}_A(L_x, A)$ by
$\ell\in \operatorname{Hom}_A(L_x, A)$ by
 \begin{equation*}
(g\ell)(v) = g(\ell(g^{-1}v)) \textrm{for } v\in L_{gx}.
\end{equation*}
\begin{equation*}
(g\ell)(v) = g(\ell(g^{-1}v)) \textrm{for } v\in L_{gx}.
\end{equation*} Let ![]() $L^\vee=\underline{\operatorname{Hom}}_{\mathcal{O}_X}(L, \mathcal{O}_X)$. We claim that
$L^\vee=\underline{\operatorname{Hom}}_{\mathcal{O}_X}(L, \mathcal{O}_X)$. We claim that ![]() $L^\vee$ is an equivariant line bundle. In fact, from the definition, one can easily check that
$L^\vee$ is an equivariant line bundle. In fact, from the definition, one can easily check that ![]() $g\ell$ is in the fibre over gx and
$g\ell$ is in the fibre over gx and ![]() $(L^\vee)_{x} \to (L^\vee)_{gx}$ is A-linear. The only nontrivial part is the naturality. In other words, for
$(L^\vee)_{x} \to (L^\vee)_{gx}$ is A-linear. The only nontrivial part is the naturality. In other words, for ![]() $f:A \to B$, we have to show that the following diagram commutes
$f:A \to B$, we have to show that the following diagram commutes

First, for ![]() $\ell \in \operatorname{Hom}_A(L_x,A)$, we have
$\ell \in \operatorname{Hom}_A(L_x,A)$, we have
Hence, we have
So, for ![]() $w=\sum v_i\otimes b_i \in L_{f^*x}$ from the linearity, we have
$w=\sum v_i\otimes b_i \in L_{f^*x}$ from the linearity, we have
 \begin{equation*}
\psi\circ\rho_A (g,\ell)(w)=\sum_i g(\ell(g^{-1}v_i)) \otimes b_i.
\end{equation*}
\begin{equation*}
\psi\circ\rho_A (g,\ell)(w)=\sum_i g(\ell(g^{-1}v_i)) \otimes b_i.
\end{equation*}On the other hand, we have
 \begin{equation*}
f^*g(w)=f^*g(\sum_iv_i\otimes b_i)=\sum_i gv_i \otimes b_i.
\end{equation*}
\begin{equation*}
f^*g(w)=f^*g(\sum_iv_i\otimes b_i)=\sum_i gv_i \otimes b_i.
\end{equation*}Hence, we have
 \begin{equation*}
\rho_B\circ (\varphi\times\psi)(g,\ell)(w) = (f^*gf^*\ell)(w) = f^*g(f^*\ell(f^*g^{-1}w))=f^*g(f^*\ell(\sum_ig^{-1}v_i\otimes b_i))
\end{equation*}
\begin{equation*}
\rho_B\circ (\varphi\times\psi)(g,\ell)(w) = (f^*gf^*\ell)(w) = f^*g(f^*\ell(f^*g^{-1}w))=f^*g(f^*\ell(\sum_ig^{-1}v_i\otimes b_i))
\end{equation*} \begin{equation*}
=f^*g (\sum_i \ell(g^{-1}v_i)\otimes b_i) = \sum_i g(\ell(g^{-1}v_i))\otimes b_i.
\end{equation*}
\begin{equation*}
=f^*g (\sum_i \ell(g^{-1}v_i)\otimes b_i) = \sum_i g(\ell(g^{-1}v_i))\otimes b_i.
\end{equation*} This shows that ![]() $\psi\circ\rho_A =\rho_B\circ (\varphi\times\psi)$.
$\psi\circ\rho_A =\rho_B\circ (\varphi\times\psi)$.
The canonical isomorphism
sends ![]() $(\ell, v)$ to
$(\ell, v)$ to ![]() $\ell(v)$. Since
$\ell(v)$. Since ![]() $(g\ell)(gv) = g(\ell(v))$, this isomorphism is equivariant, so the line bundle
$(g\ell)(gv) = g(\ell(v))$, this isomorphism is equivariant, so the line bundle ![]() $L^\vee$ is the inverse under tensor product.
$L^\vee$ is the inverse under tensor product.
Later, we will consider toric vector bundles in the affine setting and then glue them to obtain toric vector bundles in the general setting. An arbitrary vector bundle is trivial over an affine toric variety [Reference Gubeladze16]. For toric vector bundles, one has the following statement.
Proposition. [Reference Payne27, Proposition 2.2] Every toric vector bundle on an affine toric variety splits equivariantly as a sum of toric line bundles whose underlying line bundles are trivial.
The statement also holds in the semiring case, however, one cannot use a similar argument as in the classical proof. In fact, we prove an analogous theorem (theorem 5.17) in §5 saying that under the irreducibility assumption, any equivariant vector bundle which is trivial as a vector bundle splits equivariantly over an idempotent semifield.
Note that we can understand Sn in our exact sequence in proposition 2.14 as a scheme over ![]() $\mathbb{N}$. See Appendix B. This fact be used in the next section.
$\mathbb{N}$. See Appendix B. This fact be used in the next section.
5. Splitting of G-equivariant vector bundles on irreducible schemes
In this section, we study properties of G-equivariant vector bundles on irreducible schemes over an idempotent semifield K, where G is an irreducible algebraic group over K. In [Reference Jun, Mincheva and Tolliver18], we proved that any vector bundle on a scheme over an idempotent semifield, satisfying a certain local condition splits. In this section, we prove that for an irreducible algebraic group G over an idempotent semifield K, any G-equivariant vector bundle, which is trivial as a vector bundle, on an irreducible scheme X over K equivariantly splits. Along with other results, this result will be used to study toric vector bundles on toric schemes in later sections.
In what follows, by a scheme we mean a scheme over ![]() $\mathbb{N}$, i.e., semiring scheme, unless otherwise stated.
$\mathbb{N}$, i.e., semiring scheme, unless otherwise stated.
Definition 5.1. We say a semiring A is irreducible if the following condition holds: for any ![]() $x,y\in A$ if xy is nilpotent, then x or y is nilpotent.
$x,y\in A$ if xy is nilpotent, then x or y is nilpotent.
The usual argument for rings can be modified to prove the following.
Lemma 5.2. A semiring A is irreducible if and only if ![]() $\operatorname{Spec} A$ is irreducible.
$\operatorname{Spec} A$ is irreducible.
Because we prefer to work with irreducible schemes, we will need the following variant of Yoneda’s lemma. To any scheme X, we associate a functor of points ![]() $X(A) = \operatorname{Hom}(\mathrm{Spec} A, X)$ mapping the category of irreducible idempotent semirings to the category of sets.
$X(A) = \operatorname{Hom}(\mathrm{Spec} A, X)$ mapping the category of irreducible idempotent semirings to the category of sets.
Proposition 5.3. Let ![]() $X, Y$ be schemes over
$X, Y$ be schemes over ![]() $\mathbb{B}$ (i.e., over some an idempotent semiring). Suppose that X irreducible. There is a bijective correspondence between morphisms
$\mathbb{B}$ (i.e., over some an idempotent semiring). Suppose that X irreducible. There is a bijective correspondence between morphisms ![]() $f: X \rightarrow Y$ and natural transformations
$f: X \rightarrow Y$ and natural transformations ![]() $f_A: X(A) \rightarrow Y(A)$ of functors of points on the category of irreducible idempotent semirings.
$f_A: X(A) \rightarrow Y(A)$ of functors of points on the category of irreducible idempotent semirings.
Proof. Suppose ![]() $f, g: X \rightarrow Y$ are such that
$f, g: X \rightarrow Y$ are such that ![]() $f_A = g_A$ for all irreducible idempotent semirings A. Take an open affine cover
$f_A = g_A$ for all irreducible idempotent semirings A. Take an open affine cover ![]() $\{U_i=\operatorname{Spec} A_i\}_{i \in I}$ of X, where Ai are idempotent semirings. Observe that Ai is irreducible, because X is irreducible. The inclusion
$\{U_i=\operatorname{Spec} A_i\}_{i \in I}$ of X, where Ai are idempotent semirings. Observe that Ai is irreducible, because X is irreducible. The inclusion ![]() $\iota_i: U_i \rightarrow X$ is an element
$\iota_i: U_i \rightarrow X$ is an element ![]() $\iota_i \in X(A_i)$. Then
$\iota_i \in X(A_i)$. Then
Since this holds for all i, we have f = g.
Now suppose we are given functions ![]() $f_A: X(A) \rightarrow Y(A)$ for all irreducible idempotent semirings A, and that this is natural in A. Let Ui, Ai, and ιi be as before. For each
$f_A: X(A) \rightarrow Y(A)$ for all irreducible idempotent semirings A, and that this is natural in A. Let Ui, Ai, and ιi be as before. For each ![]() $i, j$, let
$i, j$, let ![]() $\{V_{ijk}\}$ be a cover of
$\{V_{ijk}\}$ be a cover of ![]() $U_i \cap U_j$ by affine open sets and write
$U_i \cap U_j$ by affine open sets and write ![]() $V_{ijk} = \mathrm{Spec}(B_{ijk})$. Let
$V_{ijk} = \mathrm{Spec}(B_{ijk})$. Let ![]() $\kappa_{ijk} \in X(B_{ijk})$ be the inclusion
$\kappa_{ijk} \in X(B_{ijk})$ be the inclusion ![]() $V_{ijk}\rightarrow X$. Let
$V_{ijk}\rightarrow X$. Let ![]() $\phi_{ijk}: V_{ijk} \rightarrow U_i$ be the inclusion. Note that
$\phi_{ijk}: V_{ijk} \rightarrow U_i$ be the inclusion. Note that ![]() $\iota_{i} \circ \phi_{ijk} = \kappa_{ijk}$.
$\iota_{i} \circ \phi_{ijk} = \kappa_{ijk}$.
We obtain maps
Naturality implies that
Similarly, the restriction of aj to Vijk is bijk. So ai and aj agree on Vijk for all k, which implies they agree on ![]() $U_i \cap U_j$. Since we have a collection of morphisms
$U_i \cap U_j$. Since we have a collection of morphisms ![]() $a_i: U_i \rightarrow Y$ that agree on overlaps, we obtain a morphism
$a_i: U_i \rightarrow Y$ that agree on overlaps, we obtain a morphism ![]() $g:X \to Y$ such that
$g:X \to Y$ such that ![]() $g|_{U_i} = a_i$. In particular, we have
$g|_{U_i} = a_i$. In particular, we have
It remains to show that ![]() $g_A = f_A$ for all irreducible A. We fix a morphism
$g_A = f_A$ for all irreducible A. We fix a morphism ![]() $x: \operatorname{Spec} A \rightarrow X$ and show that
$x: \operatorname{Spec} A \rightarrow X$ and show that
Consider first the case where x factors through some Ui, i.e., ![]() $x = \iota_i \circ y$ for some
$x = \iota_i \circ y$ for some ![]() $y \in U_i(A)$. By naturality, we have
$y \in U_i(A)$. By naturality, we have
and similarly for g. Since ![]() $g_{A_i} = f_{A_i}$ by construction,
$g_{A_i} = f_{A_i}$ by construction, ![]() $f_A(x) = g_A(x)$ for such x.
$f_A(x) = g_A(x)$ for such x.
We now consider the general case. Cover each ![]() $x^{-1}(U_i)$ by open affines, to get a cover
$x^{-1}(U_i)$ by open affines, to get a cover ![]() $\{W_{ij}=\operatorname{Spec} C_{ij}\}$ of
$\{W_{ij}=\operatorname{Spec} C_{ij}\}$ of ![]() $\operatorname{Spec} A$ such that
$\operatorname{Spec} A$ such that ![]() $x(W_{ij})\subseteq U_i$. Let
$x(W_{ij})\subseteq U_i$. Let ![]() $\mu_{ij}: W_{ij} \rightarrow \operatorname{Spec} A$ be the inclusion. Let
$\mu_{ij}: W_{ij} \rightarrow \operatorname{Spec} A$ be the inclusion. Let ![]() $x_{ij}: W_{ij} \rightarrow X$ be given by
$x_{ij}: W_{ij} \rightarrow X$ be given by
We have that xij factors through Ui, and hence
By rewriting in terms of x and µij and by using naturality, we have
It follows that the maps ![]() $f_A(x), g_A(x): \operatorname{Spec} A \rightarrow Y$ agree on each Wij, and thus are equal.
$f_A(x), g_A(x): \operatorname{Spec} A \rightarrow Y$ agree on each Wij, and thus are equal.
Our next task is to construct some examples of irreducible schemes over any additively idempotent semiring. We will start with some affine examples. For this, we will need the following lemma.
Lemma 5.4. Let A be an idempotent semiring and I be the nilradical of A, i.e.,
Then I is a subtractive ideal, i.e., if ![]() $a+b \in I$, then
$a+b \in I$, then ![]() $a \in I$. Moreover, if A is irreducible then I is prime.
$a \in I$. Moreover, if A is irreducible then I is prime.
Proof. I is an ideal by the same proof as the classical case.
Since ![]() $a+b \in I$, there exists
$a+b \in I$, there exists ![]() $n \in \mathbb{N}$ such that
$n \in \mathbb{N}$ such that ![]() $(a+b)^n=0$. Since A is idempotent, we have
$(a+b)^n=0$. Since A is idempotent, we have
 \begin{equation*}
(a+b)^n = \sum a^kb^{n-k} =0,
\end{equation*}
\begin{equation*}
(a+b)^n = \sum a^kb^{n-k} =0,
\end{equation*} which implies that ![]() $a^kb^{n-k}=0$ for all k, as any idempotent semiring is zero-sum-free. In particular
$a^kb^{n-k}=0$ for all k, as any idempotent semiring is zero-sum-free. In particular ![]() $a^n=0$, showing that
$a^n=0$, showing that ![]() $a \in I$. Thus I is subtractive.
$a \in I$. Thus I is subtractive.
The claim about primality follows immediately from the definition of an irreducible semiring.
Remark 5.5. For many of our results on irreducible idempotent semirings, the only place we need idempotence is to establish that if I is the nilradical then ![]() $A / I$ is zero-sum-free and
$A / I$ is zero-sum-free and ![]() $x + y \in I$ implies
$x + y \in I$ implies ![]() $x \in I$. These facts are trivially true for zero-sum-free semirings with no nontrivial nilpotents. Thus many of the below results apply in this setting as well. In particular if A is zero-sum-free (e.g.,
$x \in I$. These facts are trivially true for zero-sum-free semirings with no nontrivial nilpotents. Thus many of the below results apply in this setting as well. In particular if A is zero-sum-free (e.g., ![]() $A = \mathbb{N}$), then any monoid algebra
$A = \mathbb{N}$), then any monoid algebra ![]() $A[M]$ has no nontrivial zero-divisors.
$A[M]$ has no nontrivial zero-divisors.
The only tool for establishing a semiring is irreducible that will be needed for our focus on the toric case is proposition 5.6. However, we will prove other irreducibility results for the sake of making the theory more general.
Recall that for an ![]() $\mathbb{F}_1$-algebra M and a semiring A, by the base change
$\mathbb{F}_1$-algebra M and a semiring A, by the base change ![]() $A\otimes_{\mathbb{F}_1}M$ we mean the monoid semiring
$A\otimes_{\mathbb{F}_1}M$ we mean the monoid semiring ![]() $A[M]/\sim$, where ∼ identifies
$A[M]/\sim$, where ∼ identifies ![]() $0 \in M$ and
$0 \in M$ and ![]() $0 \in A$. See §2.3.
$0 \in A$. See §2.3.
Proposition 5.6. Let A be an irreducible idempotent semiring, and let M be an irreducible ![]() $\mathbb{F}_1$-algebra. Then the semiring
$\mathbb{F}_1$-algebra. Then the semiring ![]() $A \otimes_{\mathbb{F}_1} M$ is irreducible. Moreover, if neither A nor M have nontrivial zero-divisors, then neither does
$A \otimes_{\mathbb{F}_1} M$ is irreducible. Moreover, if neither A nor M have nontrivial zero-divisors, then neither does ![]() $A \otimes_{\mathbb{F}_1} M$. In particular for any monoid M,
$A \otimes_{\mathbb{F}_1} M$. In particular for any monoid M, ![]() $A[M]$ is irreducible, and if A has no nontrivial zero-divisors,
$A[M]$ is irreducible, and if A has no nontrivial zero-divisors, ![]() $A[M]$ does not either.
$A[M]$ does not either.
Proof. In the monoid case, we can adjoin a zero element to get to the case of an ![]() $\mathbb{F}_1$-algebra with no non-trivial zero-divisors.
$\mathbb{F}_1$-algebra with no non-trivial zero-divisors.
Let ![]() $x, y\in A \otimes_{\mathbb{F}_1} M$ be such that xy is nilpotent. We wish to show either x or y is nilpotent. Write
$x, y\in A \otimes_{\mathbb{F}_1} M$ be such that xy is nilpotent. We wish to show either x or y is nilpotent. Write
 \begin{equation*}
x = \sum_{m\in M} x_m [m],
\end{equation*}
\begin{equation*}
x = \sum_{m\in M} x_m [m],
\end{equation*} where ![]() $x_m \in A$, and we have a similar expansion for y. Then
$x_m \in A$, and we have a similar expansion for y. Then
 \begin{equation*} \sum_{m, n \in M} x_m y_n [mn] \end{equation*}
\begin{equation*} \sum_{m, n \in M} x_m y_n [mn] \end{equation*} is nilpotent. Thus, from lemma 5.4, ![]() $x_m y_n [mn]$ is nilpotent for all
$x_m y_n [mn]$ is nilpotent for all ![]() $m, n\in M$. Then there is some k such that
$m, n\in M$. Then there is some k such that ![]() $(x_m y_n)^k [(mn)^k] = 0$. Since non-zero elements of M form a basis for
$(x_m y_n)^k [(mn)^k] = 0$. Since non-zero elements of M form a basis for ![]() $A \otimes_{\mathbb{F}_1} M$, either
$A \otimes_{\mathbb{F}_1} M$, either ![]() $[(mn)^k] = 0$ or
$[(mn)^k] = 0$ or ![]() $(x_m y_n)^k = 0$.
$(x_m y_n)^k = 0$.
If for all ![]() $n\in M$ either yn is nilpotent or
$n\in M$ either yn is nilpotent or ![]() $[n]$ is nilpotent, then
$[n]$ is nilpotent, then ![]() $y = \sum y_n [n]$ lies in the nilradical, and we are done. Otherwise choose
$y = \sum y_n [n]$ lies in the nilradical, and we are done. Otherwise choose ![]() $n\in M$ such that neither yn nor
$n\in M$ such that neither yn nor ![]() $[n]$ is nilpotent and choose
$[n]$ is nilpotent and choose ![]() $m\in M$ arbitrarily. In the case that
$m\in M$ arbitrarily. In the case that ![]() $x_m y_n$ is nilpotent, since yn is not, irreducibility of A tells us xm is nilpotent. In the other case where
$x_m y_n$ is nilpotent, since yn is not, irreducibility of A tells us xm is nilpotent. In the other case where ![]() $[mn]$ is nilpotent, irreducibility of M tells us
$[mn]$ is nilpotent, irreducibility of M tells us ![]() $[m]$ is nilpotent. Thus for all
$[m]$ is nilpotent. Thus for all ![]() $m\in M$,
$m\in M$, ![]() $x_m [m]$ is nilpotent and thus
$x_m [m]$ is nilpotent and thus ![]() $x = \sum x_m [m]$ is nilpotent. This shows irreducibility of
$x = \sum x_m [m]$ is nilpotent. This shows irreducibility of ![]() $A\otimes_{\mathbb{F}_1}M$.
$A\otimes_{\mathbb{F}_1}M$.
For the second assertion, if neither A nor M have non-trivial zero-divisors (in particular all nilpotents are trivial), suppose xy = 0 (in particular xy is nilpotent). We may follow the argument above, and in the first case of the previous paragraph, we obtain that for all ![]() $n\in M$, either yn is nilpotent (so
$n\in M$, either yn is nilpotent (so ![]() $y_n = 0$) or
$y_n = 0$) or ![]() $[n]$ is nilpotent (so
$[n]$ is nilpotent (so ![]() $[n] = 0$). Either way
$[n] = 0$). Either way ![]() $y = \sum y_n [n] = 0$. In the remaining case, as in the previous paragraph, we get that for each m, xm or
$y = \sum y_n [n] = 0$. In the remaining case, as in the previous paragraph, we get that for each m, xm or ![]() $[m]$ is nilpotent, and as in the previous case, we get
$[m]$ is nilpotent, and as in the previous case, we get ![]() $x = \sum x_m [m] = 0$.
$x = \sum x_m [m] = 0$.
Note that the above result is false over rings, as seen in the case ![]() $A = \mathbb{C}$ and
$A = \mathbb{C}$ and ![]() $M = \mathbb{Z}/2\mathbb{Z}$. Also note that while we generally assume commutativity, the above result holds for noncommutative
$M = \mathbb{Z}/2\mathbb{Z}$. Also note that while we generally assume commutativity, the above result holds for noncommutative ![]() $\mathbb{F}_1$-algebras as well.
$\mathbb{F}_1$-algebras as well.
The following lemma will be useful for studying irreducibility of quotient semirings.
Lemma 5.7. Let A be an irreducible idempotent semiring. Let ∼ be a congruence generated by a collection of pairs ![]() $(x_i, y_i)$ with the property that for each i in the index set, either both xi and yi are nilpotent or both are non-nilpotent. Then if
$(x_i, y_i)$ with the property that for each i in the index set, either both xi and yi are nilpotent or both are non-nilpotent. Then if ![]() $x \sim y$, either both x and y are nilpotent or both are non-nilpotent. Moreover, the quotient
$x \sim y$, either both x and y are nilpotent or both are non-nilpotent. Moreover, the quotient ![]() $A / \sim$ is irreducible. If A has no nontrivial zero-divisors, then neither does
$A / \sim$ is irreducible. If A has no nontrivial zero-divisors, then neither does ![]() $A / \sim$.
$A / \sim$.
Proof. Let P be the nilradical, which is a subtractive prime ideal by lemma 5.4. Then ![]() $A / P$ is a zero-sum-free semiring with no nontrivial zero-divisors. This implies the map
$A / P$ is a zero-sum-free semiring with no nontrivial zero-divisors. This implies the map ![]() $\phi: A/ P \rightarrow \mathbb{B}$ given by
$\phi: A/ P \rightarrow \mathbb{B}$ given by ![]() $\phi(0) = 0$ and
$\phi(0) = 0$ and ![]() $\phi(x) = 1$ for x ≠ 0 is a homomorphism. We consider instead the epimorphism
$\phi(x) = 1$ for x ≠ 0 is a homomorphism. We consider instead the epimorphism ![]() $\psi: A \rightarrow \mathbb{B}$ obtained by composing with the quotient map; explicitly
$\psi: A \rightarrow \mathbb{B}$ obtained by composing with the quotient map; explicitly ![]() $\psi(x)$ is 0 or 1 according to whether x is nilpotent.
$\psi(x)$ is 0 or 1 according to whether x is nilpotent.
Write ![]() $x \equiv y$ if x and y are both nilpotent or both non-nilpotent. Since this is equivalent to
$x \equiv y$ if x and y are both nilpotent or both non-nilpotent. Since this is equivalent to ![]() $\psi(x) = \psi(y)$, ≡ is a congruence. By assumption it contains all generators of the congruence ∼. Thus, if
$\psi(x) = \psi(y)$, ≡ is a congruence. By assumption it contains all generators of the congruence ∼. Thus, if ![]() $x \sim y$, then
$x \sim y$, then ![]() $x \equiv y$, which is the first part of the result.
$x \equiv y$, which is the first part of the result.
For the second part of the result, suppose ![]() $\bar{x} \bar{y} \in A / \sim$ is nilpotent. Pick lifts
$\bar{x} \bar{y} \in A / \sim$ is nilpotent. Pick lifts ![]() $x, y\in A$, and observe that for some k,
$x, y\in A$, and observe that for some k, ![]() $(xy)^k \sim 0$. Thus
$(xy)^k \sim 0$. Thus ![]() $(xy)^k$ is nilpotent, which implies xy is nilpotent. By irreducibility, either x or y is nilpotent, which implies the same for
$(xy)^k$ is nilpotent, which implies xy is nilpotent. By irreducibility, either x or y is nilpotent, which implies the same for ![]() $\bar{x}$ or
$\bar{x}$ or ![]() $\bar{y}$.
$\bar{y}$.
If A has no nontrivial zero-divisors, suppose ![]() $\bar{x} \bar{y} = 0$. It is nilpotent, so we may follow the previous paragraph to obtain that x or y is nilpotent. But A has no nontrivial nilpotents, so x = 0 or y = 0 and hence
$\bar{x} \bar{y} = 0$. It is nilpotent, so we may follow the previous paragraph to obtain that x or y is nilpotent. But A has no nontrivial nilpotents, so x = 0 or y = 0 and hence ![]() $\bar{x} = 0$ or
$\bar{x} = 0$ or ![]() $\bar{y} = 0$.
$\bar{y} = 0$.
One application of the above result is to the tropicalization of a variety not contained in the union of the coordinate hyperplanes. Note that a monoid does not have an absorbing element 0, and hence it is always irreducible as it cannot have nilpotent elements.
Proposition 5.8. Let K be a valued field, M be a monoid, and ![]() $I\subseteq K[M]$ be an ideal. Let
$I\subseteq K[M]$ be an ideal. Let ![]() $R = K[M] / I$, where I does not contain any element of M. Let A be the tropicalization of R, i.e., the quotient of
$R = K[M] / I$, where I does not contain any element of M. Let A be the tropicalization of R, i.e., the quotient of ![]() $\mathbb{T}[M]$ by bend relations corresponding to elements of I. Then A has no nontrivial zero-divisors, in particular A is irreducible.
$\mathbb{T}[M]$ by bend relations corresponding to elements of I. Then A has no nontrivial zero-divisors, in particular A is irreducible.
Proof. Observe that ![]() $\mathbb{T}[M]$ has no nontrivial zero-divisors by proposition 5.6. Let ∼ be the congruence of
$\mathbb{T}[M]$ has no nontrivial zero-divisors by proposition 5.6. Let ∼ be the congruence of ![]() $\mathbb{T}[M]$ generated by bend relations. Let vK be the valuation on K.
$\mathbb{T}[M]$ generated by bend relations. Let vK be the valuation on K.
Let ![]() $f \in I \subseteq K[M]$. Write
$f \in I \subseteq K[M]$. Write ![]() $f = \sum a_i [m_i]$ with the ai all non-zero. If f has no terms (i.e., f = 0), then the set of bend relations for f is empty and the bend congruence is just the diagonal congruence. If there is only one term then
$f = \sum a_i [m_i]$ with the ai all non-zero. If f has no terms (i.e., f = 0), then the set of bend relations for f is empty and the bend congruence is just the diagonal congruence. If there is only one term then ![]() $[m_1] = f / a_1 \in I \cap M$ contradicting the hypothesis. Thus we may assume there are at least two non-zero terms.
$[m_1] = f / a_1 \in I \cap M$ contradicting the hypothesis. Thus we may assume there are at least two non-zero terms.
For each i, consider the corresponding bend relation
 \begin{equation*}
\sum_j v_K(a_j) [m_j] \sim \sum_{j \neq i} v_K(a_j) [m_j].
\end{equation*}
\begin{equation*}
\sum_j v_K(a_j) [m_j] \sim \sum_{j \neq i} v_K(a_j) [m_j].
\end{equation*} Since f contains more than one term, both sums are nonempty. Moreover each term is non-zero. So the bend relation identifies a non-zero element with another non-zero element. Since ![]() $\mathbb{T}[M]$ is reduced, the bend relation identifies two non-nilpotents. Thus the result follows from lemma 5.7.
$\mathbb{T}[M]$ is reduced, the bend relation identifies two non-nilpotents. Thus the result follows from lemma 5.7.
Remark 5.9. Note that one may also prove proposition 5.8 by using [Reference Jun, Mincheva and Tolliver18, Corollary 6.11].
Next we show that a tensor product of irreducible idempotent semirings is irreducible. We do so by viewing the tensor product as a quotient of a monoid algebra.
Proposition 5.10. Let R be an idempotent semiring, and let ![]() $A, B$ be irreducible R-algebras. Assume that the maps
$A, B$ be irreducible R-algebras. Assume that the maps ![]() $R \rightarrow A$ and
$R \rightarrow A$ and ![]() $R \rightarrow B$ have trivial kernels (which is automatic if R is a semifield) (Here, a kernel does not mean an equalizer, but it means simply the inverse image of 0). Then
$R \rightarrow B$ have trivial kernels (which is automatic if R is a semifield) (Here, a kernel does not mean an equalizer, but it means simply the inverse image of 0). Then ![]() $A \otimes_R B$ is irreducible.
$A \otimes_R B$ is irreducible.
Proof. If we forget the addition structure on B, we can view it as an irreducible ![]() $\mathbb{F}_1$-algebra. We can then construct the A-algebra
$\mathbb{F}_1$-algebra. We can then construct the A-algebra ![]() $A \otimes_{\mathbb{F}_1} B$. This is irreducible by proposition 5.6. By abuse of notation, we denote it
$A \otimes_{\mathbb{F}_1} B$. This is irreducible by proposition 5.6. By abuse of notation, we denote it ![]() $A[B]$, since this makes the asymmetry in how we treat A and B more clear.
$A[B]$, since this makes the asymmetry in how we treat A and B more clear.
Define a congruence ∼ on ![]() $A[B]$ generated by
$A[B]$ generated by ![]() $[b_1] + [b_2] \sim [b_1 + b_2]$ for
$[b_1] + [b_2] \sim [b_1 + b_2]$ for ![]() $b_1, b_2 \in B$ and
$b_1, b_2 \in B$ and ![]() $r \sim [r]$ for
$r \sim [r]$ for ![]() $r \in R$ (i.e., ∼ identifies the copy of R for B with the one for A). Because the structure maps have trivial kernel,
$r \in R$ (i.e., ∼ identifies the copy of R for B with the one for A). Because the structure maps have trivial kernel, ![]() $r^k = 0$ if and only if
$r^k = 0$ if and only if ![]() $[r]^k = 0$, so r is nilpotent if and only if
$[r]^k = 0$, so r is nilpotent if and only if ![]() $[r]$ is nilpotent. If
$[r]$ is nilpotent. If ![]() $[b_1 + b_2]$ is nilpotent, there is some k such that
$[b_1 + b_2]$ is nilpotent, there is some k such that ![]() $[(b_1 + b_2)^k] = 0$ and hence
$[(b_1 + b_2)^k] = 0$ and hence ![]() $(b_1 + b_2)^k = 0$, i.e.,
$(b_1 + b_2)^k = 0$, i.e., ![]() $b_1 + b_2$ is nilpotent. By lemma 5.4, this implies b 1 and b 2 are nilpotents in B so
$b_1 + b_2$ is nilpotent. By lemma 5.4, this implies b 1 and b 2 are nilpotents in B so ![]() $[b_1], [b_2] \in A[B]$ are nilpotent, and hence
$[b_1], [b_2] \in A[B]$ are nilpotent, and hence ![]() $[b_1] + [b_2]$ is nilpotent. Conversely if
$[b_1] + [b_2]$ is nilpotent. Conversely if ![]() $[b_1] + [b_2]$ is nilpotent, lemma 5.4 implies each term is nilpotent, so
$[b_1] + [b_2]$ is nilpotent, lemma 5.4 implies each term is nilpotent, so ![]() $b_1, b_2$ are nilpotent, and hence
$b_1, b_2$ are nilpotent, and hence ![]() $[b_1 + b_2]$ is nilpotent. So no generator of ∼ identifies a nilpotent element with a non-nilpotent. Thus
$[b_1 + b_2]$ is nilpotent. So no generator of ∼ identifies a nilpotent element with a non-nilpotent. Thus ![]() $A[B] / \sim$ is irreducible by lemma 5.7.
$A[B] / \sim$ is irreducible by lemma 5.7.
![]() $A[B]$ has the universal property that a homomorphism
$A[B]$ has the universal property that a homomorphism ![]() $A[B] \rightarrow S$ corresponds to a pair of a semiring homomorphism
$A[B] \rightarrow S$ corresponds to a pair of a semiring homomorphism ![]() $A \rightarrow S$ and an
$A \rightarrow S$ and an ![]() $\mathbb{F}_1$-algebra homomorphism
$\mathbb{F}_1$-algebra homomorphism ![]() $B \rightarrow S$ (viewed S as a multiplicative monoid with 0). A homomorphism
$B \rightarrow S$ (viewed S as a multiplicative monoid with 0). A homomorphism ![]() $(A[B] / \sim) \rightarrow S$ corresponds to a homomorphism
$(A[B] / \sim) \rightarrow S$ corresponds to a homomorphism ![]() $\phi: A[B] \rightarrow S$ such that
$\phi: A[B] \rightarrow S$ such that ![]() $\phi(r) = \phi([r])$ for all
$\phi(r) = \phi([r])$ for all ![]() $r\in R$ and
$r\in R$ and ![]() $\phi([b_1]) + \phi([b_2]) = \phi([b_1 + b_2])$ for all
$\phi([b_1]) + \phi([b_2]) = \phi([b_1 + b_2])$ for all ![]() $b_1, b_2 \in B$. This in turn corresponds to a pair of a homomorphism
$b_1, b_2 \in B$. This in turn corresponds to a pair of a homomorphism ![]() $\phi_A: A \rightarrow S$ and an
$\phi_A: A \rightarrow S$ and an ![]() $\mathbb{F}_1$ algebra homomorphism
$\mathbb{F}_1$ algebra homomorphism ![]() $\phi_B: B\rightarrow S$ such that ϕA and ϕB agree on R and such that ϕB preserves addition (i.e., ϕB is in fact a semiring homomorphism).
$\phi_B: B\rightarrow S$ such that ϕA and ϕB agree on R and such that ϕB preserves addition (i.e., ϕB is in fact a semiring homomorphism).
The universal property of tensor products of semirings says that a homomorphism ![]() $A \otimes_R B \rightarrow S$ corresponds to a pair of homomorphisms
$A \otimes_R B \rightarrow S$ corresponds to a pair of homomorphisms ![]() $A \rightarrow S$ and
$A \rightarrow S$ and ![]() $B\rightarrow S$ which agree on R. Thus,
$B\rightarrow S$ which agree on R. Thus, ![]() $A \otimes_R B \cong A[B] / \sim$. Since
$A \otimes_R B \cong A[B] / \sim$. Since ![]() $A[B] / \sim$ is irreducible, so is
$A[B] / \sim$ is irreducible, so is ![]() $A \otimes_R B$.
$A \otimes_R B$.
Remark 5.11. The above result fails for classical schemes, e.g., ![]() $\mathbb{C} \otimes_{\mathbb{R}} \mathbb{C}$ is not even connected.
$\mathbb{C} \otimes_{\mathbb{R}} \mathbb{C}$ is not even connected.
The following lemma is useful in order to prove similar irreducibility results for non-affine schemes.
Lemma 5.12. Let X be a sober space with an open cover ![]() $\{U_i\}$ such that each Ui is irreducible. Construct a graph whose vertices correspond to sets of the open cover. Two vertices i and j are connected by an edge if
$\{U_i\}$ such that each Ui is irreducible. Construct a graph whose vertices correspond to sets of the open cover. Two vertices i and j are connected by an edge if ![]() $U_i \cap U_j \neq \emptyset$. This graph is connected if and only if X is irreducible.
$U_i \cap U_j \neq \emptyset$. This graph is connected if and only if X is irreducible.
Proof. If X is irreducible, clearly the graph is connected. Conversely, suppose that the graph is connected. If Ui and Uj are nondisjoint, then ![]() $U_i \cap U_j$ is an open subset of the irreducible space Ui and therefore contains the generic point of Ui. Similarly, it contains the generic point of Uj. But
$U_i \cap U_j$ is an open subset of the irreducible space Ui and therefore contains the generic point of Ui. Similarly, it contains the generic point of Uj. But ![]() $U_i \cap U_j$ is irreducible (as it is an open subset of an irreducible space), so it contains a unique generic point. Thus, if i and j are connected by an edge, Ui and Uj share the same generic point. Since the graph is connected, all of the Ui share the same generic point η.
$U_i \cap U_j$ is irreducible (as it is an open subset of an irreducible space), so it contains a unique generic point. Thus, if i and j are connected by an edge, Ui and Uj share the same generic point. Since the graph is connected, all of the Ui share the same generic point η.
Let U be an open set. There is some i such that ![]() $U \cap U_i \neq \emptyset$. Since
$U \cap U_i \neq \emptyset$. Since ![]() $U \cap U_i$ is an open set in the irreducible space Ui, it contains the generic point η. Since all open sets contain η, no two open sets can be disjoint.
$U \cap U_i$ is an open set in the irreducible space Ui, it contains the generic point η. Since all open sets contain η, no two open sets can be disjoint.
As an application of this result we show that the product of irreducible schemes is irreducible.
Proposition 5.13. Let X and Y be irreducible schemes over an idempotent semifield K. Then ![]() $X \times_K Y$ is irreducible.
$X \times_K Y$ is irreducible.
Proof. First, we note that the construction of the fibred product in the semiring setting is the same as in the classical case of rings. One can check the same arguments go through mutatis mutandis.
Now, from the construction of the fibred product ![]() $X\times_KY$, if U is an open subset of X, then the preimage of U under
$X\times_KY$, if U is an open subset of X, then the preimage of U under ![]() $\pi_1: X \times_K Y \rightarrow X$ is isomorphic to
$\pi_1: X \times_K Y \rightarrow X$ is isomorphic to ![]() $U \times_K Y$. Moreover, the product of affine schemes corresponds to the tensor product of semirings.
$U \times_K Y$. Moreover, the product of affine schemes corresponds to the tensor product of semirings.
Let ![]() $U_i = \operatorname{Spec} A_i$ be an open affine cover of X and
$U_i = \operatorname{Spec} A_i$ be an open affine cover of X and ![]() $V_j = \operatorname{Spec} B_j$ be an open affine cover of Y.
$V_j = \operatorname{Spec} B_j$ be an open affine cover of Y. ![]() $X \times_K Y$ has an open cover by open subschemes of the form
$X \times_K Y$ has an open cover by open subschemes of the form ![]() $\pi_1^{-1}(U_i) = U_i \times_K Y$, and these in turn may be covered by open subschemes of the form
$\pi_1^{-1}(U_i) = U_i \times_K Y$, and these in turn may be covered by open subschemes of the form ![]() $U_i \times_K V_j = \operatorname{Spec} A_i \otimes_K B_j$. By proposition 5.10, each
$U_i \times_K V_j = \operatorname{Spec} A_i \otimes_K B_j$. By proposition 5.10, each ![]() $U_i \times_K V_j$ is irreducible.
$U_i \times_K V_j$ is irreducible.
Next, we consider the graph associated with this open cover (with an edge linking open subsets if they are not disjoint). This graph has vertices of the form (i, j), where i and j belong to the index sets of the covers ![]() $\{U_i \}$ and
$\{U_i \}$ and ![]() $\{V_j \}$, respectively.
$\{V_j \}$, respectively.
If Ui and Uk are not disjoint, then  $\pi_1^{-1}(U_i \cap U_k) \cong (U_i \cap U_j) \times_K Y$, so the left side is nonempty. In particular,
$\pi_1^{-1}(U_i \cap U_k) \cong (U_i \cap U_j) \times_K Y$, so the left side is nonempty. In particular, ![]() $U_i \times_K Y$ and
$U_i \times_K Y$ and ![]() $U_j \times_K Y$ are not disjoint open subschemes. We may apply this with Vj in place of Y to obtain that
$U_j \times_K Y$ are not disjoint open subschemes. We may apply this with Vj in place of Y to obtain that ![]() $U_i \times_K V_j$ and
$U_i \times_K V_j$ and ![]() $U_k \times_K V_j$ are not disjoint open subschemes of
$U_k \times_K V_j$ are not disjoint open subschemes of ![]() $X \times_K V_j \subseteq X \times_K Y$. So for each j we get an edge linking (i, j) to (k, j). Similarly if Vj and Vl are not disjoint then for each i,
$X \times_K V_j \subseteq X \times_K Y$. So for each j we get an edge linking (i, j) to (k, j). Similarly if Vj and Vl are not disjoint then for each i, ![]() $U_i \times_K V_j$ intersects
$U_i \times_K V_j$ intersects ![]() $U_i \times_K V_l$. So we get edges linking (i, j) to (i, l).
$U_i \times_K V_l$. So we get edges linking (i, j) to (i, l).
Thus the product graph of the graphs associated with the covers ![]() $\{U_i \}$ and
$\{U_i \}$ and ![]() $\{V_j \}$ is a spanning subgraph of the graph associated with the product cover. Since the product of connected graphs is connected, the result follows from lemma 5.12.
$\{V_j \}$ is a spanning subgraph of the graph associated with the product cover. Since the product of connected graphs is connected, the result follows from lemma 5.12.
Next we will establish irreducibility of toric schemes over an idempotent semiring.
Let Δ be a fan. Construct a graph ![]() $G_{\Delta}$ whose vertices correspond to cones in Δ in which two vertices
$G_{\Delta}$ whose vertices correspond to cones in Δ in which two vertices ![]() $\sigma, \tau \in \Delta$ are linked by an edge if σ is a face of τ. Then,
$\sigma, \tau \in \Delta$ are linked by an edge if σ is a face of τ. Then, ![]() $G_{\Delta}$ is connected since
$G_{\Delta}$ is connected since ![]() $\{0\}$ is a face of any cone in Δ.
$\{0\}$ is a face of any cone in Δ.
Proposition 5.14. Let X be the toric scheme associated with a fan Δ over an irreducible idempotent semiring R. Then X is irreducible.
Proof. X has an open cover ![]() $\{U_{\sigma} \}$ (by nonempty sets) indexed by the cones in Δ in which
$\{U_{\sigma} \}$ (by nonempty sets) indexed by the cones in Δ in which ![]() $U_{\sigma} \subseteq U_\tau$ whenever σ is a face of τ. Now, the result directly follows from lemma 5.12 applied to
$U_{\sigma} \subseteq U_\tau$ whenever σ is a face of τ. Now, the result directly follows from lemma 5.12 applied to ![]() $G_{\Delta}$.
$G_{\Delta}$.
Lemma 5.15. Let X be a connected scheme over ![]() $\mathbb{N}$. Let R and S be semirings. Then any morphism
$\mathbb{N}$. Let R and S be semirings. Then any morphism ![]() $X \to \operatorname{Spec} (R\oplus S)$ factors through
$X \to \operatorname{Spec} (R\oplus S)$ factors through ![]() $\operatorname{Spec} R$ or
$\operatorname{Spec} R$ or ![]() $\operatorname{Spec} S$.
$\operatorname{Spec} S$.
Proof. We begin with the affine case in which ![]() $X = \operatorname{Spec} A$, where we are looking at a homomorphism
$X = \operatorname{Spec} A$, where we are looking at a homomorphism ![]() $\phi: R\oplus S\rightarrow A$. Let
$\phi: R\oplus S\rightarrow A$. Let ![]() $e = \phi(1, 0)$ and
$e = \phi(1, 0)$ and ![]() $f = \phi(0, 1)$. Since
$f = \phi(0, 1)$. Since ![]() $(1, 0) + (0, 1) = (1, 1)$ and
$(1, 0) + (0, 1) = (1, 1)$ and ![]() $(1, 0)(0, 1) = (0, 0)$, it follows that (e, f) forms an idempotent pair. By connectedness either e = 0 or f = 0. Without loss of generality consider the latter case. Then
$(1, 0)(0, 1) = (0, 0)$, it follows that (e, f) forms an idempotent pair. By connectedness either e = 0 or f = 0. Without loss of generality consider the latter case. Then ![]() $\phi(r, s) = re + sf = re$ so ϕ factors through the projection
$\phi(r, s) = re + sf = re$ so ϕ factors through the projection ![]() $R\oplus S\rightarrow R$. Note that unless X is the empty scheme, ϕ cannot factor through both projections because then we would have
$R\oplus S\rightarrow R$. Note that unless X is the empty scheme, ϕ cannot factor through both projections because then we would have ![]() $\phi(1, 1) = \phi(0, 0)$ contradicting that homomorphisms are unital.
$\phi(1, 1) = \phi(0, 0)$ contradicting that homomorphisms are unital.
Now consider the non-affine case. Construct a cover by affine open subsets ![]() $\{U_i\}$. Let
$\{U_i\}$. Let ![]() $\phi:X \to \operatorname{Spec}(R\oplus S)$. Then, the restriction
$\phi:X \to \operatorname{Spec}(R\oplus S)$. Then, the restriction ![]() $\phi|_{U_i}$ factors through either
$\phi|_{U_i}$ factors through either ![]() $\operatorname{Spec} R$ or
$\operatorname{Spec} R$ or ![]() $\operatorname{Spec} S$. Suppose that for two indices i and j,
$\operatorname{Spec} S$. Suppose that for two indices i and j, ![]() $\phi|_{U_i}$ factors through
$\phi|_{U_i}$ factors through ![]() $\operatorname{Spec} R$,
$\operatorname{Spec} R$, ![]() $\phi|_{U_j}$ factors through
$\phi|_{U_j}$ factors through ![]() $\operatorname{Spec} S$, and
$\operatorname{Spec} S$, and ![]() $U_i\cap U_j \neq \emptyset$. Then, we obtain a contradiction by letting W be an affine open subset of
$U_i\cap U_j \neq \emptyset$. Then, we obtain a contradiction by letting W be an affine open subset of ![]() $U_i\cap U_j$ and observing that
$U_i\cap U_j$ and observing that ![]() $\phi|_W$ factors through both
$\phi|_W$ factors through both ![]() $\operatorname{Spec} R$ and
$\operatorname{Spec} R$ and ![]() $\operatorname{Spec} S$.
$\operatorname{Spec} S$.
Let U be the union of all Ui such that ![]() $\phi|_{U_i}$ factors through
$\phi|_{U_i}$ factors through ![]() $\operatorname{Spec} R$ and V be the union of all Ui such that
$\operatorname{Spec} R$ and V be the union of all Ui such that ![]() $\phi|_{U_i}$ factors through
$\phi|_{U_i}$ factors through ![]() $\operatorname{Spec} S$. We just showed U and V are disjoint, and clearly they cover X. So one of them is empty; without loss of generality it is V, and so all
$\operatorname{Spec} S$. We just showed U and V are disjoint, and clearly they cover X. So one of them is empty; without loss of generality it is V, and so all ![]() $\phi|_{U_i}$ factor through R. Hence so does ϕ.
$\phi|_{U_i}$ factor through R. Hence so does ϕ.
With these preliminaries on irreducible sets out of the way, we turn to studying the obstruction to an equivariant vector bundle being a sum of one-dimensional bundles equivariantly. We will start by considering a sort of a ‘vector bundle over a set’ rather than a scheme and will later use the functor of points viewpoint to reduce the scheme-theoretic case to this one.
Let A be an irreducible idempotent semiring, G a group, and X a G-set, and let ![]() $n \in \mathbb{N}$. Let
$n \in \mathbb{N}$. Let ![]() $E = X \times A^n$, and for each
$E = X \times A^n$, and for each ![]() $x \in X$, let
$x \in X$, let ![]() $E_x = \{x\} \times A^n$, which is an A-module in the obvious way. Let
$E_x = \{x\} \times A^n$, which is an A-module in the obvious way. Let ![]() $e_i\in A^n$ be the standard basis and
$e_i\in A^n$ be the standard basis and ![]() $e_i(x) = (x, e_i)$ be the corresponding basis of Ex. Fix a G-action on E such that the projection
$e_i(x) = (x, e_i)$ be the corresponding basis of Ex. Fix a G-action on E such that the projection ![]() $E\rightarrow X$ is equivariant and for each
$E\rightarrow X$ is equivariant and for each ![]() $g\in G$ and
$g\in G$ and ![]() $x\in X$, the induced maps
$x\in X$, the induced maps ![]() $g: E_x\rightarrow E_{gx}$ on fibres are A-linear.
$g: E_x\rightarrow E_{gx}$ on fibres are A-linear.
Lemma 5.16. With the same notation as above, there is a unique map ![]() $\phi: G \times X\rightarrow S_n$ such that
$\phi: G \times X\rightarrow S_n$ such that ![]() $g e_i(x)$ is a scalar multiple of
$g e_i(x)$ is a scalar multiple of ![]() $e_{\phi(g, x)(i)}(gx)$ for all
$e_{\phi(g, x)(i)}(gx)$ for all ![]() $(g, x)\in G\times X$.
$(g, x)\in G\times X$.
Proof. Fix ![]() $g\in G$ and
$g\in G$ and ![]() $x\in X$. We consider two bases of Egx: we have the basis
$x\in X$. We consider two bases of Egx: we have the basis ![]() $\{e_i(gx)\}$ and the basis
$\{e_i(gx)\}$ and the basis ![]() $\{g e_i(x)\}$. Because A is an irreducible (hence connected) zero-sum-free semiring and Egx is a free A-module, the basis is unique up to reordering and scalar multiplication (see remark A.5). Thus, there is some permutation σ and some units
$\{g e_i(x)\}$. Because A is an irreducible (hence connected) zero-sum-free semiring and Egx is a free A-module, the basis is unique up to reordering and scalar multiplication (see remark A.5). Thus, there is some permutation σ and some units ![]() $a_i\in A^\times$ such that
$a_i\in A^\times$ such that ![]() $g e_i(x) = a_i e_{\sigma(i)}(gx)$. The desired map ϕ is the map that sends (g, x) to this
$g e_i(x) = a_i e_{\sigma(i)}(gx)$. The desired map ϕ is the map that sends (g, x) to this ![]() $\sigma \in S_n$. Note that ϕ is unique because a basis vector cannot be a multiple of another element of the basis.
$\sigma \in S_n$. Note that ϕ is unique because a basis vector cannot be a multiple of another element of the basis.
To understand the significance of lemma 5.16, note that if the map ϕ in the lemma sends every element to ![]() $1\in S_n$, then
$1\in S_n$, then ![]() $g e_i(x)$ is a scalar multiple of
$g e_i(x)$ is a scalar multiple of ![]() $e_i(gx)$. Thinking of E as essentially an equivariant vector bundle this would mean that
$e_i(gx)$. Thinking of E as essentially an equivariant vector bundle this would mean that ![]() $X \times \mathrm{span}(e_i)$ is an equivariant line subbundle, and E would decompose into equivariant line bundles. Of course this is all taking place over sets rather than schemes, so our definition of equivariant vector bundle does not quite apply.
$X \times \mathrm{span}(e_i)$ is an equivariant line subbundle, and E would decompose into equivariant line bundles. Of course this is all taking place over sets rather than schemes, so our definition of equivariant vector bundle does not quite apply.
Morally we expect that in the scheme-theoretic case, we should have a similar map ![]() $G \times X \rightarrow S_n$ acting as the obstruction to decomposing an equivariant vector bundle which is trivial as a vector bundle into line bundles. We will do this only in the case where X and G are irreducible. Note that furthermore, under these irreducibility assumptions, we should intuitively expect the map to be trivial for connectedness reasons.
$G \times X \rightarrow S_n$ acting as the obstruction to decomposing an equivariant vector bundle which is trivial as a vector bundle into line bundles. We will do this only in the case where X and G are irreducible. Note that furthermore, under these irreducibility assumptions, we should intuitively expect the map to be trivial for connectedness reasons.
Now, fix an irreducible scheme X over an idempotent semifield K and a vector bundle E on X. For any irreducible idempotent semiring A and ![]() $x:Y=\operatorname{Spec} A \to X$, we let
$x:Y=\operatorname{Spec} A \to X$, we let ![]() $E_x=x^*E(\operatorname{Spec} A)$ as before. Let’s recall some more notations. We have
$E_x=x^*E(\operatorname{Spec} A)$ as before. Let’s recall some more notations. We have
 \begin{equation*}
E(A)=\bigsqcup_{x \in X(A)}E_x.
\end{equation*}
\begin{equation*}
E(A)=\bigsqcup_{x \in X(A)}E_x.
\end{equation*}Also, there is a canonical projection
where ![]() $\pi_A(y)=x$ if and only if
$\pi_A(y)=x$ if and only if ![]() $y \in E_x$.
$y \in E_x$.
Theorem 5.17 5.17 Let X be an irreducible scheme over an idempotent semifield K and G be an irreducible algebraic group over K acting on X. Let E be a G-equivariant vector bundle on X which is trivial as a vector bundle. Then E is a direct sum of equivariant line bundles.
Proof. For any irreducible idempotent K-algebra A, we consider the group G(A) of A-valued points of G and its action on the sets X(A) and E(A). Pick a basis ei for E and observe that this induces a basis ![]() $x^*(e_i)$ of Ex for each
$x^*(e_i)$ of Ex for each ![]() $x\in X(A)$. Note that this is essentially due to the fact that
$x\in X(A)$. Note that this is essentially due to the fact that ![]() $x^*$ and
$x^*$ and ![]() $x_*$ are adjoint functors as in the case for rings (lemma 3.8), implying that if
$x_*$ are adjoint functors as in the case for rings (lemma 3.8), implying that if ![]() $E=\mathcal{O}_X^n$, then
$E=\mathcal{O}_X^n$, then ![]() $x^*E=\mathcal{O}_{\operatorname{Spec} A}^n$ since a left adjoint functor preserves colimits. It follows that
$x^*E=\mathcal{O}_{\operatorname{Spec} A}^n$ since a left adjoint functor preserves colimits. It follows that ![]() $E_x=A^n$, and hence we can identify E(A) with
$E_x=A^n$, and hence we can identify E(A) with ![]() $X(A) \times A^n$.
$X(A) \times A^n$.
Now, equivariance of the bundle E means that G(A) acts on E(A) in a manner that is linear on fibres (definition 4.1 (3)) and that it makes the projection ![]() $\pi_A:E(A)\rightarrow X(A)$ equivariant (definition 4.1 (2)). Apply lemma 5.16 to the G(A)-action on
$\pi_A:E(A)\rightarrow X(A)$ equivariant (definition 4.1 (2)). Apply lemma 5.16 to the G(A)-action on ![]() $E(A)\rightarrow X(A)$. We obtain for each A, a map
$E(A)\rightarrow X(A)$. We obtain for each A, a map ![]() $\phi_A: G(A) \times X(A) \rightarrow S_n$ such that
$\phi_A: G(A) \times X(A) \rightarrow S_n$ such that ![]() $g e_i(x)$ is a scalar multiple of
$g e_i(x)$ is a scalar multiple of ![]() $e_{\phi_A(g, x)(i)}(gx)$ for all
$e_{\phi_A(g, x)(i)}(gx)$ for all ![]() $(g, x)\in G(A) \times X(A)$.
$(g, x)\in G(A) \times X(A)$.
First, we want to show this map is natural. Fix a morphism ![]() $f: \operatorname{Spec} B \rightarrow \operatorname{Spec} A$. The induced map
$f: \operatorname{Spec} B \rightarrow \operatorname{Spec} A$. The induced map ![]() $f^*: X(A)\rightarrow X(B)$ sends a point
$f^*: X(A)\rightarrow X(B)$ sends a point ![]() $x:\operatorname{Spec} A\rightarrow X$ to
$x:\operatorname{Spec} A\rightarrow X$ to ![]() $x\circ f$, and the induced map
$x\circ f$, and the induced map ![]() $f^*: G(A)\rightarrow G(B)$ is described similarly.
$f^*: G(A)\rightarrow G(B)$ is described similarly.
Let ![]() $\alpha:G \times_K X \to X$ be a G-action on X. Then for each K-algebra A, one has
$\alpha:G \times_K X \to X$ be a G-action on X. Then for each K-algebra A, one has
Since the action α is a morphism of schemes, it induces a natural transformation of functors of points, i.e., for ![]() $g \in G(A)$ and
$g \in G(A)$ and ![]() $x \in X(A)$, one has
$x \in X(A)$, one has
The induced map ![]() $f^*: E(A)\rightarrow E(B)$ sends
$f^*: E(A)\rightarrow E(B)$ sends ![]() $e_i(x)$ to
$e_i(x)$ to
By (1) of definition 4.1, similar to (13), for any ![]() $e\in E(A)$ and
$e\in E(A)$ and ![]() $g\in G(A)$, we have
$g\in G(A)$, we have
Observe that
is a scalar multiple of
because ![]() $ge_i(x)$ is a multiple of
$ge_i(x)$ is a multiple of ![]() $e_{\phi_A(g, x)(i)}(gx)$. We claim the following:
$e_{\phi_A(g, x)(i)}(gx)$. We claim the following:
which is precisely the naturality result we want to prove. Note that ![]() $f^*$ does not occur on the right side because Sn is a constant functor, so
$f^*$ does not occur on the right side because Sn is a constant functor, so ![]() $f^*$ is the identity here.
$f^*$ is the identity here.
To see (17), define for ![]() $g' \in G(B)$ and
$g' \in G(B)$ and ![]() $x' \in X(B)$,
$x' \in X(B)$,
 \begin{equation}
\psi(g',x')=\begin{cases}
\phi_B(g',x') & \textrm{if } (g', x') \neq (f^*(g), f^*(x)),\\
\phi_A(g, x) & \textrm{if } (g', x') = (f^*(g), f^*(x)).
\end{cases}
\end{equation}
\begin{equation}
\psi(g',x')=\begin{cases}
\phi_B(g',x') & \textrm{if } (g', x') \neq (f^*(g), f^*(x)),\\
\phi_A(g, x) & \textrm{if } (g', x') = (f^*(g), f^*(x)).
\end{cases}
\end{equation} Then for any ![]() $g' \in G(B)$ and
$g' \in G(B)$ and ![]() $x' \in X(B)$, we see that
$x' \in X(B)$, we see that ![]() $g' e_i(x')$ is a multiple of
$g' e_i(x')$ is a multiple of ![]() $e_{\psi(g', x')(i)}(g'x')$; when
$e_{\psi(g', x')(i)}(g'x')$; when ![]() $(g', x') = (f^*(g), f^*(x))$ this is because (15) is a multiple of (16), and otherwise this holds because it is true for ϕB. Now the uniqueness in the defining property of ϕB (in lemma 5.16) implies
$(g', x') = (f^*(g), f^*(x))$ this is because (15) is a multiple of (16), and otherwise this holds because it is true for ϕB. Now the uniqueness in the defining property of ϕB (in lemma 5.16) implies ![]() $\phi_B = \psi$, so in particular
$\phi_B = \psi$, so in particular ![]() $\phi_B(f^*(g), f^*(x)) = \phi_A(g, x)$, as claimed.
$\phi_B(f^*(g), f^*(x)) = \phi_A(g, x)$, as claimed.
We thus have constructed a natural map ![]() $(G \times_K X)(A) \rightarrow S_n = S_n(A)$. Moreover, it follows from proposition 5.13 that
$(G \times_K X)(A) \rightarrow S_n = S_n(A)$. Moreover, it follows from proposition 5.13 that ![]() $G \times_K X$ is irreducible. Therefore, from lemma 5.3, this natural transformation comes from a morphism of schemes
$G \times_K X$ is irreducible. Therefore, from lemma 5.3, this natural transformation comes from a morphism of schemes ![]() $\phi: G \times_K X \rightarrow S_n$. Since
$\phi: G \times_K X \rightarrow S_n$. Since ![]() $G\times_K X$ is connected, and Sn is the spectrum of a direct sum of
$G\times_K X$ is connected, and Sn is the spectrum of a direct sum of ![]() $n!$ copies of K, ϕ is constant, i.e., there is some
$n!$ copies of K, ϕ is constant, i.e., there is some ![]() $\sigma \in S_n$ such that ϕ factors through the inclusion
$\sigma \in S_n$ such that ϕ factors through the inclusion ![]() $\operatorname{Spec} K\rightarrow S_n$ corresponding to the point σ. The same must be true of the corresponding maps on functors of points. Thus,
$\operatorname{Spec} K\rightarrow S_n$ corresponding to the point σ. The same must be true of the corresponding maps on functors of points. Thus, ![]() $\phi_A(g, x) = \sigma$ for all
$\phi_A(g, x) = \sigma$ for all ![]() $(g, x)\in G(A) \times X(A)$. So we obtain that for any
$(g, x)\in G(A) \times X(A)$. So we obtain that for any ![]() $(g, x)\in G(A) \times X(A)$,
$(g, x)\in G(A) \times X(A)$, ![]() $g e_i(x)$ is a scalar multiple of
$g e_i(x)$ is a scalar multiple of ![]() $e_{\sigma (i)}(gx)$. By applying this to g = 1, we must have σ = 1, so
$e_{\sigma (i)}(gx)$. By applying this to g = 1, we must have σ = 1, so ![]() $g e_i(x)$ is a scalar multiple of
$g e_i(x)$ is a scalar multiple of ![]() $e_i(gx)$.
$e_i(gx)$.
Let Li be the line bundle contained in E given as a sheaf by ![]() $L_i(U) = \mathrm{span}(e_i|_U)$. Its functor of points is such that
$L_i(U) = \mathrm{span}(e_i|_U)$. Its functor of points is such that ![]() $L_i(A)$ is the set of pairs (x, e) such that
$L_i(A)$ is the set of pairs (x, e) such that ![]() $x\in X(A)$, and
$x\in X(A)$, and ![]() $e\in \mathrm{span}(e_i(x))\subseteq E_x$. We saw
$e\in \mathrm{span}(e_i(x))\subseteq E_x$. We saw ![]() $g e_i(x)$ is a scalar multiple of
$g e_i(x)$ is a scalar multiple of ![]() $e_i(gx)$ so belongs to
$e_i(gx)$ so belongs to ![]() $L_i(A)$, and the same is true for ge where
$L_i(A)$, and the same is true for ge where ![]() $e\in L_i(A)$ since any such e is a multiple of
$e\in L_i(A)$ since any such e is a multiple of ![]() $e_i(x)$ for some x. Since
$e_i(x)$ for some x. Since ![]() $ge\in L_i(A)$ for
$ge\in L_i(A)$ for ![]() $g\in G(A)$ and
$g\in G(A)$ and ![]() $e\in L_i(A)$, it follows that the G(A) action on E(A) descends to an action on
$e\in L_i(A)$, it follows that the G(A) action on E(A) descends to an action on ![]() $L_i(A)$, making
$L_i(A)$, making ![]() $L_i(A)$ equivariant. Even without equivariance, we of course have
$L_i(A)$ equivariant. Even without equivariance, we of course have ![]() $E = \bigoplus L_i$, and since Li is equivariant, this implies the result.
$E = \bigoplus L_i$, and since Li is equivariant, this implies the result.
Corollary 5.18. Let X be a toric scheme over an idempotent semifield K and G be the algebraic torus over K. Let E be an equivariant vector bundle which is trivial as a vector bundle. Then E is a direct sum of equivariant line bundles.
Remark 5.19. In the non-affine case, there are non-trivial (toric) line bundles both in the classical case [Reference Perling and Schröer29] and the tropical case [Reference Jun, Mincheva and Tolliver17].
6. Classification of equivariant vector bundles
Throughout this section, unless stated otherwise, we let K denote either a semiring or a monoid (with an absorbing element). As in the case for rings and semirings, by a monoid scheme over K, when K is a monoid, we mean a monoid scheme X with a map to ![]() $\operatorname{Spec} K$. Most of the results below hold for both semiring schemes and monoid schemes, with the same proof for both cases. And we will need both cases in order to compare equivariant line bundles on toric schemes over idempotent semirings with those on the underlying monoid schemes.
$\operatorname{Spec} K$. Most of the results below hold for both semiring schemes and monoid schemes, with the same proof for both cases. And we will need both cases in order to compare equivariant line bundles on toric schemes over idempotent semirings with those on the underlying monoid schemes.
The following result justifies thinking of morphisms ![]() $X\rightarrow \text{GL}_1$ as units of X.
$X\rightarrow \text{GL}_1$ as units of X.
Lemma 6.1. Let X be a scheme (resp. monoid scheme) over a semiring (resp. monoid) K. Let ![]() $\text{GL}_1 = \operatorname{Spec} K[t, t^{-1}]$. Then there is a natural isomorphism
$\text{GL}_1 = \operatorname{Spec} K[t, t^{-1}]$. Then there is a natural isomorphism ![]() $\mathrm{Hom}_{\operatorname{Spec} K}(X, \text{GL}_1) \simeq \Gamma(X, \mathcal{O}_X^\times)$.
$\mathrm{Hom}_{\operatorname{Spec} K}(X, \text{GL}_1) \simeq \Gamma(X, \mathcal{O}_X^\times)$.
Proof. We prove the case for semirings. The case for monoids is similar.
Note that we have a canonical global section  $t \in \Gamma(GL_1, \mathcal{O}_{\text{GL}_1}^\times)$, so
$t \in \Gamma(GL_1, \mathcal{O}_{\text{GL}_1}^\times)$, so ![]() $f: X\rightarrow \text{GL}_1$ induces a global section
$f: X\rightarrow \text{GL}_1$ induces a global section ![]() $f^*t \in \Gamma(X, \mathcal{O}_X^\times)$. It is natural, because given
$f^*t \in \Gamma(X, \mathcal{O}_X^\times)$. It is natural, because given ![]() $g: Y\rightarrow \text{GL}_1$, the induced map on
$g: Y\rightarrow \text{GL}_1$, the induced map on ![]() $\mathrm{Hom}_{\operatorname{Spec} K}(-, \text{GL}_1)$ sends f to
$\mathrm{Hom}_{\operatorname{Spec} K}(-, \text{GL}_1)$ sends f to ![]() $f\circ g$, while the induced map on
$f\circ g$, while the induced map on ![]() $\Gamma(-, \mathcal{O}_-^\times)$ sends
$\Gamma(-, \mathcal{O}_-^\times)$ sends ![]() $f^* t$ to
$f^* t$ to ![]() $g^* f^* t = (f\circ g)^* t$.
$g^* f^* t = (f\circ g)^* t$.
To show it is an isomorphism, we begin with the affine case, where ![]() $X = \operatorname{Spec} A$ for some semiring A and so
$X = \operatorname{Spec} A$ for some semiring A and so ![]() $\Gamma(X, \mathcal{O}_X^\times) = A^\times$. The universal property of
$\Gamma(X, \mathcal{O}_X^\times) = A^\times$. The universal property of ![]() $K[t, t^{-1}]$ asserts that morphisms
$K[t, t^{-1}]$ asserts that morphisms
are in bijection with units of A, and that the corresponding element of ![]() $A^\times$ is
$A^\times$ is ![]() $f(t) = f^* t$. So this bijection is the natural map from before.
$f(t) = f^* t$. So this bijection is the natural map from before.
Now consider the general case. Fix an open affine cover ![]() $\{U_i \}$ and let
$\{U_i \}$ and let ![]() $\iota_i: U_i\rightarrow X$ be the inclusion. For each
$\iota_i: U_i\rightarrow X$ be the inclusion. For each ![]() $i, j$, fix an open affine cover
$i, j$, fix an open affine cover ![]() $\{V_{ijk} \}$ of
$\{V_{ijk} \}$ of ![]() $U_i \cap U_j$ with
$U_i \cap U_j$ with ![]() $V_{ijk} = V_{jik}$, and let
$V_{ijk} = V_{jik}$, and let ![]() $\phi_{ijk}: V_{ijk} \rightarrow U_i$ be the inclusion. Given
$\phi_{ijk}: V_{ijk} \rightarrow U_i$ be the inclusion. Given ![]() $u \in \Gamma(X, \mathcal{O}_X^\times)$, we obtain elements
$u \in \Gamma(X, \mathcal{O}_X^\times)$, we obtain elements  $u_i = u\mid_{U_i} \in \Gamma(U_i, \mathcal{O}_{U_i}^\times)$ which satisfy the following condition:
$u_i = u\mid_{U_i} \in \Gamma(U_i, \mathcal{O}_{U_i}^\times)$ which satisfy the following condition:
We let fi be the morphism corresponding to ui; note that the restrictions of fi and fj to each Vijk agree. Our goal is to show there is a unique ![]() $f: X\rightarrow GL_1$ satisfying
$f: X\rightarrow GL_1$ satisfying ![]() $u = f^* t$.
$u = f^* t$.
Given a morphism ![]() $f: X\rightarrow GL_1$, we have
$f: X\rightarrow GL_1$, we have
Thus ![]() $f^* t = u$ if and only if
$f^* t = u$ if and only if ![]() $(f\mid_{U_i})^* t = u_i$. By the affine case of this result, this holds if and only if
$(f\mid_{U_i})^* t = u_i$. By the affine case of this result, this holds if and only if ![]() $f\mid_{U_i}$ is the morphism corresponding to ui, i.e., if and only if
$f\mid_{U_i}$ is the morphism corresponding to ui, i.e., if and only if ![]() $f\mid_{U_i} = f_i$. But since the fi agree on overlaps they glue together to give a unique morphism satisfying this property.
$f\mid_{U_i} = f_i$. But since the fi agree on overlaps they glue together to give a unique morphism satisfying this property.
Let K be a semiring or a monoid. Let X and Y be schemes over K. For each K-algebra A, there is an one-to-one correspondence between the points ![]() $t \in (X\times_KY)(A)$ and the pairs
$t \in (X\times_KY)(A)$ and the pairs ![]() $(x,y) \in X(A) \times Y(A)$ satisfying the following condition
$(x,y) \in X(A) \times Y(A)$ satisfying the following condition
where ![]() $g_X:X \to \operatorname{Spec} K$ and
$g_X:X \to \operatorname{Spec} K$ and ![]() $g_Y:Y \to \operatorname{Spec} K$ are the structure maps. From now on, we replace each
$g_Y:Y \to \operatorname{Spec} K$ are the structure maps. From now on, we replace each ![]() $t \in (X\times_KY)(A)$, with a pair
$t \in (X\times_KY)(A)$, with a pair ![]() $(x,y) \in X(A) \times Y(A)$ satisfying (19).
$(x,y) \in X(A) \times Y(A)$ satisfying (19).
The following result shows how any equivariant structure on the trivial line bundle ![]() $\mathcal{O}_X$ gives rise to a unit on
$\mathcal{O}_X$ gives rise to a unit on ![]() $G \times_K X$. This will be the key to classifying equivariant structures on
$G \times_K X$. This will be the key to classifying equivariant structures on ![]() $\mathcal{O}_X$. Note that this unit could potentially depend on the choice of basis vector. We can just choose the basis vector to be
$\mathcal{O}_X$. Note that this unit could potentially depend on the choice of basis vector. We can just choose the basis vector to be ![]() $1\in \mathcal{O}_X$, but since that 1 is not preserved by line bundle automorphisms, the resulting unit is not completely canonical.
$1\in \mathcal{O}_X$, but since that 1 is not preserved by line bundle automorphisms, the resulting unit is not completely canonical.
To proceed, we need a notion of equivariant vector bundles on a monoid scheme X.
Definition 6.2. Let K be a monoid, X be a scheme over K, and G be a group scheme over K acting on X. By an equivariant vector bundle E on X, we mean a vector bundle E (locally free sheaf) on X together with an action of G(A) for each K-algebra A satisfying the same conditions as in definition 4.1.
Remark 6.3. One can observe that all statements in §3 except proposition 3.20 are valid for locally free sheaves on monoid schemes as proofs do not use something specific to semirings. In fact, the proofs for rings can be modified to proof the semiring case and the monoid case.
Lemma 6.4. Let K be a semiring or monoid. Let X be a scheme over K and G be a group scheme over K acting on X. Let L be an equivariant line bundle on X which is trivial as a line bundle and let v be a basis vector for the global sections of L. Then there is a unique morphism ![]() $u: G \times_K X \rightarrow GL_1$ such that for each K-algebra A, each
$u: G \times_K X \rightarrow GL_1$ such that for each K-algebra A, each ![]() $(g, x) \in (G\times_KX)(A)$, the morphism
$(g, x) \in (G\times_KX)(A)$, the morphism ![]() $u_A: (G\times_KX)(A) \rightarrow GL_1(A)$ satisfies
$u_A: (G\times_KX)(A) \rightarrow GL_1(A)$ satisfies ![]() $u_A(g, x) v_{gx} = g v_x$.
$u_A(g, x) v_{gx} = g v_x$.
Proof. We prove the case for semirings. The case for monoids is similar.
We will construct u via its functor of points. Let v be a basis vector for global sections for L. Since vx is a basis vector for the free module Lx, gvx is a basis vector for Lgx. But vgx is also a basis vector, so there is a unique ![]() $a\in GL_1(A)$ such that
$a\in GL_1(A)$ such that ![]() $a v_{gx} = g v_x$. We let
$a v_{gx} = g v_x$. We let ![]() $u_A(g,x)=a$.
$u_A(g,x)=a$.
We have thus constructed a unique map uA such that ![]() $u_A(g, x) v_{gx} = g v_x$ holds. To obtain the map u, we must show uA is natural in A. Fix a morphism
$u_A(g, x) v_{gx} = g v_x$ holds. To obtain the map u, we must show uA is natural in A. Fix a morphism ![]() $f:\operatorname{Spec} B \to \operatorname{Spec} A$. As in the proof of theorem 5.17, we let the induced maps be
$f:\operatorname{Spec} B \to \operatorname{Spec} A$. As in the proof of theorem 5.17, we let the induced maps be ![]() $f^*:X(A) \to X(B)$,
$f^*:X(A) \to X(B)$, ![]() $f^*:G(A) \to G(B)$, and
$f^*:G(A) \to G(B)$, and ![]() $f^*:L(A) \to L(B)$. Since
$f^*:L(A) \to L(B)$. Since ![]() $f^*(gx)=f^*(g)f^*(x)$, we have
$f^*(gx)=f^*(g)f^*(x)$, we have
Recall that ![]() $v_{f^* x}$ is the result of pulling v back along
$v_{f^* x}$ is the result of pulling v back along ![]() $f^* x : \operatorname{Spec} B \rightarrow X$, while vx is the pullback along
$f^* x : \operatorname{Spec} B \rightarrow X$, while vx is the pullback along ![]() $x: \operatorname{Spec} A \rightarrow X$. Thus
$x: \operatorname{Spec} A \rightarrow X$. Thus ![]() $v_{f^* x}$ is the pullback of vx along
$v_{f^* x}$ is the pullback of vx along ![]() $f: \operatorname{Spec} B \rightarrow \operatorname{Spec} A$. In other words,
$f: \operatorname{Spec} B \rightarrow \operatorname{Spec} A$. In other words, ![]() $v_{f^*x} = f^* v_x$, where the latter
$v_{f^*x} = f^* v_x$, where the latter ![]() $f^*$ denotes the induced map
$f^*$ denotes the induced map ![]() $f^*:L(A)\rightarrow L(B)$.
$f^*:L(A)\rightarrow L(B)$.
Thus we have
But applying ![]() $f^*$ to both sides of
$f^*$ to both sides of
gives
Thus ![]() $u_B(f^* g, f^* x) = u_A(g, x)$, which is the desired naturality.
$u_B(f^* g, f^* x) = u_A(g, x)$, which is the desired naturality.
The next step is to determine which units of ![]() $G \times_K X$ arise this way.
$G \times_K X$ arise this way.
Lemma 6.5. With the notation and assumptions of lemma 6.4, for ![]() $(g, h, x) \in (G\times_K G \times_K X)(A)$, we have
$(g, h, x) \in (G\times_K G \times_K X)(A)$, we have ![]() $u_A(gh, x) = u_A(h, x) u_A(g, hx)$ and
$u_A(gh, x) = u_A(h, x) u_A(g, hx)$ and ![]() $u_A(1, x) = 1$.
$u_A(1, x) = 1$.
Proof. To show the first part of the statement, observe that
Since vghx is a basis vector, the first part of the statement follows. Similarly, the second half of the statement follows from ![]() $u_A(1, x) v_x = 1 v_x = v_x$.
$u_A(1, x) v_x = 1 v_x = v_x$.
Definition 6.6. With the same notation as above, a map ![]() $u:G \times_K X \to \text{GL}_1$ is said to be principal if for any K-algebra A and for
$u:G \times_K X \to \text{GL}_1$ is said to be principal if for any K-algebra A and for ![]() $(g, h, x) \in (G\times_K G \times_K X)(A)$, one has
$(g, h, x) \in (G\times_K G \times_K X)(A)$, one has
Note that Eq. (20) implies that ![]() $u_A(1, x) = 1$.
$u_A(1, x) = 1$.
Lemma 6.7. Let K be either a semiring or a monoid. Let X be a scheme over K and G be a group scheme over K acting on X. Let ![]() $u: G \times_K X \rightarrow \text{GL}_1$ be a principal morphism. Then there is an equivariant line bundle and a basis vector v such that u arises from the construction of lemma 6.4. In other words,
$u: G \times_K X \rightarrow \text{GL}_1$ be a principal morphism. Then there is an equivariant line bundle and a basis vector v such that u arises from the construction of lemma 6.4. In other words,
Proof. We choose any trivial line bundle L and basis vector v. To construct the equivariant structure, we define the action ![]() $\rho_A:G(A) \times L(A) \rightarrow L(A)$ by
$\rho_A:G(A) \times L(A) \rightarrow L(A)$ by
By construction this action is linear and satisfies ![]() $u_A(g, x) v_{gx} = g v_x$. We must check that it is actually a group action, that it is compatible with the action on X, and that it is natural in A.
$u_A(g, x) v_{gx} = g v_x$. We must check that it is actually a group action, that it is compatible with the action on X, and that it is natural in A.
To see that it is a group action, observe that
which is the desired homomorphism property. Also 1 acts via ![]() $1(a v_x) = u_A(1, x) a v_x = a v_x$. The action is compatible with the action on X because
$1(a v_x) = u_A(1, x) a v_x = a v_x$. The action is compatible with the action on X because ![]() $g(a v_x) = a u_A(g, x) v_{gx}$ lies over gx.
$g(a v_x) = a u_A(g, x) v_{gx}$ lies over gx.
To show that the action is natural in A, let ![]() $f:\operatorname{Spec} B \to \operatorname{Spec} A$, and
$f:\operatorname{Spec} B \to \operatorname{Spec} A$, and ![]() $f^*$ be as in the proof of lemma 6.4. We need to show that the following diagram commutes:
$f^*$ be as in the proof of lemma 6.4. We need to show that the following diagram commutes:

Now for ![]() $(g,av_x) \in G(A) \times L(A)$, we have
$(g,av_x) \in G(A) \times L(A)$, we have
 \begin{align*}
f^*\rho_A(g,av_x)&=f^*(au_A(g,x)v_{gx})=au_A(g,x)f^*(v_{gx})\\
&=au_A(g,x)v_{f^*({gx})}=au_A(g,x)v_{f^*gf^*x}.
\end{align*}
\begin{align*}
f^*\rho_A(g,av_x)&=f^*(au_A(g,x)v_{gx})=au_A(g,x)f^*(v_{gx})\\
&=au_A(g,x)v_{f^*({gx})}=au_A(g,x)v_{f^*gf^*x}.
\end{align*}On the other hand,
From the functoriallity of u, we have
implying that
We can now classify actions on the trivial bundle ![]() $\mathcal{O}_X$ which make it into an equivariant line bundle.
$\mathcal{O}_X$ which make it into an equivariant line bundle.
Proposition 6.8. Let K be a semiring or a monoid. Let X be a scheme over K and G be a group scheme over K acting on X. Then there is a one-to-one correspondence between G-actions on ![]() $\mathcal{O}_X$ which make
$\mathcal{O}_X$ which make ![]() $\mathcal{O}_X$ an equivariant line bundle and principal morphisms
$\mathcal{O}_X$ an equivariant line bundle and principal morphisms ![]() $u: G \times_K X \rightarrow GL_1$. Moreover, this correspondence is a group isomorphism, where the first set is viewed as a group under tensor product, and the second is a group under pointwise multiplication.
$u: G \times_K X \rightarrow GL_1$. Moreover, this correspondence is a group isomorphism, where the first set is viewed as a group under tensor product, and the second is a group under pointwise multiplication.
Remark 6.9. Proposition 4.3 shows that the tensor product of equivariant line bundles is an equivariant line bundle, that ![]() $\mathcal{O}_X$ with the trivial action is the tensor product identity and that the dual line bundle is the inverse. Since
$\mathcal{O}_X$ with the trivial action is the tensor product identity and that the dual line bundle is the inverse. Since ![]() $\mathcal{O}_X \otimes \mathcal{O}_X = \mathcal{O}_X = \operatorname{Hom}(\mathcal{O}_X, \mathcal{O}_X)$, the set of equivariant line bundles whose underlying line bundle is
$\mathcal{O}_X \otimes \mathcal{O}_X = \mathcal{O}_X = \operatorname{Hom}(\mathcal{O}_X, \mathcal{O}_X)$, the set of equivariant line bundles whose underlying line bundle is ![]() $\mathcal{O}_X$ is closed under tensor products and duals and hence forms a group.
$\mathcal{O}_X$ is closed under tensor products and duals and hence forms a group.
Proof of proposition 6.8
We have already proved that equivariant structures on ![]() $\mathcal{O}_X$ uniquely give rise to principal morphisms u (lemmas 6.4 and 6.5), and that every such u arises in this way (lemma 6.7).
$\mathcal{O}_X$ uniquely give rise to principal morphisms u (lemmas 6.4 and 6.5), and that every such u arises in this way (lemma 6.7).
Next we prove the uniqueness. Consider two actions ![]() $\alpha, \beta: G \times_K \mathcal{O}_X \rightarrow \mathcal{O}_X$ which give rise to the same morphism u. Any element of L(A) can be written
$\alpha, \beta: G \times_K \mathcal{O}_X \rightarrow \mathcal{O}_X$ which give rise to the same morphism u. Any element of L(A) can be written ![]() $a 1_x$ for some
$a 1_x$ for some ![]() $a\in A$ and
$a\in A$ and ![]() $x\in X(A)$. Under both actions, linearity and the definition of u give
$x\in X(A)$. Under both actions, linearity and the definition of u give
and hence so both actions are the same. In other words, such u arises from a unique equivariant structure on ![]() $\mathcal{O}_X$.
$\mathcal{O}_X$.
Finally, we show this bijective correspondence is a homomorphism. Let ![]() $L, L'$ be equivariant line bundles with basis sections v and w, respectively. Let
$L, L'$ be equivariant line bundles with basis sections v and w, respectively. Let ![]() $u, u', \phi: G \times_K X \rightarrow \mathrm{GL}_1$ correspond to equivariant structures of
$u, u', \phi: G \times_K X \rightarrow \mathrm{GL}_1$ correspond to equivariant structures of ![]() $L, L', L\otimes L'$, respectively. Then by definition of ϕ and of the action on the tensor product,
$L, L', L\otimes L'$, respectively. Then by definition of ϕ and of the action on the tensor product,
On the other hand, by definition of u and u ′,
So ![]() $\phi = uu'$, which implies the correspondence in question is a group homomorphism.
$\phi = uu'$, which implies the correspondence in question is a group homomorphism.
The relationship in lemma 6.1, between units of the global sections of ![]() $G\times_K X$ and morphisms
$G\times_K X$ and morphisms ![]() $G\times_K X \to \text{GL}_1$, lets us phrase proposition 6.8 entirely in terms of units.
$G\times_K X \to \text{GL}_1$, lets us phrase proposition 6.8 entirely in terms of units.
Let K be a semiring or a monoid and X be a scheme over K and G be a group scheme over K acting on X. Let ![]() $m, a, p: G\times_K G \times_K X \rightarrow X$ be the maps induced by the multiplication on G, the action of G on X, and the projection which drops the first factor, respectively, and let
$m, a, p: G\times_K G \times_K X \rightarrow X$ be the maps induced by the multiplication on G, the action of G on X, and the projection which drops the first factor, respectively, and let ![]() $i: X \rightarrow G \times_K X$ be the map which inserts the identity element in the first component. Let
$i: X \rightarrow G \times_K X$ be the map which inserts the identity element in the first component. Let ![]() $\mu: GL_1 \times_K GL_1\rightarrow GL_1$ denote multiplication.
$\mu: GL_1 \times_K GL_1\rightarrow GL_1$ denote multiplication.
Corollary 6.10. With the same notation as above, there is a group isomorphism between the group of equivariant line bundle structures on ![]() $\mathcal{O}_X$ and the group of units
$\mathcal{O}_X$ and the group of units  $u \in \Gamma(G\times_K X, \mathcal{O}_{G\times_K X}^\times)$ satisfying
$u \in \Gamma(G\times_K X, \mathcal{O}_{G\times_K X}^\times)$ satisfying ![]() $i^*u = 1$ and
$i^*u = 1$ and ![]() $\mu \circ (a^* u, p^*u) = m^*(u)$.
$\mu \circ (a^* u, p^*u) = m^*(u)$.
In the case of toric varieties, we can use the above result to relate the tropical setting to the ![]() $\mathbb{F}_1$-setting as follows. We will interchangeably use the terms
$\mathbb{F}_1$-setting as follows. We will interchangeably use the terms ![]() $\mathbb{F}_1$-schemes and monoid schemes. By a group scheme over
$\mathbb{F}_1$-schemes and monoid schemes. By a group scheme over ![]() $\mathbb{F}_1$ we mean a group object in the category of
$\mathbb{F}_1$ we mean a group object in the category of ![]() $\mathbb{F}_1$-schemes. In the following, for monoid schemes
$\mathbb{F}_1$-schemes. In the following, for monoid schemes ![]() $X, Y$ we simply write X × Y instead of
$X, Y$ we simply write X × Y instead of ![]() $X\times_{\mathbb{F}_1}Y$. Likewise, for semiring schemes XR and YR over a semiring R, we write
$X\times_{\mathbb{F}_1}Y$. Likewise, for semiring schemes XR and YR over a semiring R, we write ![]() $X_R\times Y_R$ for
$X_R\times Y_R$ for ![]() $X_R\times_{R}Y_R$.
$X_R\times_{R}Y_R$.
Lemma 6.11. Let X be a toric ![]() $\mathbb{F}_1$-scheme and G be a group scheme over
$\mathbb{F}_1$-scheme and G be a group scheme over ![]() $\mathbb{F}_1$. Let K be an idempotent semifield. Then, we have
$\mathbb{F}_1$. Let K be an idempotent semifield. Then, we have
 \begin{equation}
\Gamma(G_K\times X_K, \mathcal{O}_{G_K\times X_{K}}^\times) = \Gamma(G\times X, K^\times) \times \Gamma(G\times X, \mathcal{O}_{G\times X}^\times).
\end{equation}
\begin{equation}
\Gamma(G_K\times X_K, \mathcal{O}_{G_K\times X_{K}}^\times) = \Gamma(G\times X, K^\times) \times \Gamma(G\times X, \mathcal{O}_{G\times X}^\times).
\end{equation}Proof. We first consider the case when X and G are affine. Let ![]() $X=\operatorname{Spec} M$ and
$X=\operatorname{Spec} M$ and ![]() $G=\operatorname{Spec} N$. Then,
$G=\operatorname{Spec} N$. Then,
and since tensor products preserve colimits
Hence, we have
 \begin{equation*}
\Gamma(G_K\times X_K, \mathcal{O}_{G_K\times X_K}^\times) = (K[N\otimes_{\mathbb{F}_1}M])^\times.
\end{equation*}
\begin{equation*}
\Gamma(G_K\times X_K, \mathcal{O}_{G_K\times X_K}^\times) = (K[N\otimes_{\mathbb{F}_1}M])^\times.
\end{equation*}It follows from [Reference Jun, Mincheva and Tolliver17, Proposition 3.4] that
On the other hand, one can easily check that
showing the claimed identity for affine G and X.
For general G and X, we cover ![]() $G_K \times X_K$ by affine open cover
$G_K \times X_K$ by affine open cover ![]() $\mathcal{U}_K$ obtained by affine open subsets of
$\mathcal{U}_K$ obtained by affine open subsets of ![]() $\mathcal{U}=\{U_i\times V_j\}$, where Ui (resp. Vj) are affine open subsets of G (resp. X). Note that this is possible by [Reference Jun, Mincheva and Tolliver17, Lemma 3.1]. Then, as in [Reference Jun, Mincheva and Tolliver17, Theorem 3.8], by using the affine case, one can obtain isomorphisms of Čech cochains
$\mathcal{U}=\{U_i\times V_j\}$, where Ui (resp. Vj) are affine open subsets of G (resp. X). Note that this is possible by [Reference Jun, Mincheva and Tolliver17, Lemma 3.1]. Then, as in [Reference Jun, Mincheva and Tolliver17, Theorem 3.8], by using the affine case, one can obtain isomorphisms of Čech cochains
 \begin{equation*}
\mathbf{C}^k(\mathcal{U}_K,\mathcal{O}_{G_K\times X_K}^\times) = \mathbf{C}^k(\mathcal{U},K^\times \times \mathcal{O}_{G\times X}^\times),
\end{equation*}
\begin{equation*}
\mathbf{C}^k(\mathcal{U}_K,\mathcal{O}_{G_K\times X_K}^\times) = \mathbf{C}^k(\mathcal{U},K^\times \times \mathcal{O}_{G\times X}^\times),
\end{equation*}showing the desired identity (23).
Proposition 6.12. Let X be a toric ![]() $\mathbb{F}_1$-scheme and G be a group scheme over
$\mathbb{F}_1$-scheme and G be a group scheme over ![]() $\mathbb{F}_1$. Let K be an idempotent semifield. Suppose G × X is connected. Then there is an isomorphism between the group of G-equivariant line bundle structures on
$\mathbb{F}_1$. Let K be an idempotent semifield. Suppose G × X is connected. Then there is an isomorphism between the group of G-equivariant line bundle structures on ![]() $\mathcal{O}_X$ and the group of GK-equivariant line bundle structures on
$\mathcal{O}_X$ and the group of GK-equivariant line bundle structures on ![]() $\mathcal{O}_{X_K}$.
$\mathcal{O}_{X_K}$.
Proof. Let  $u \in \Gamma(G_K\times X_K, \mathcal{O}_{G_K\times X_K}^\times)$. We write
$u \in \Gamma(G_K\times X_K, \mathcal{O}_{G_K\times X_K}^\times)$. We write ![]() $u=(u_1,u_2)$ under the isomorphism in lemma 6.11. Under a connectedness assumption, u 1 is constant, and hence the identity
$u=(u_1,u_2)$ under the isomorphism in lemma 6.11. Under a connectedness assumption, u 1 is constant, and hence the identity
together with the fact that ![]() $K^\times$ is a group (so that
$K^\times$ is a group (so that ![]() $x^2 = x$ implies x = 1) implies that u 1 is 1. It follows that u actually lies in
$x^2 = x$ implies x = 1) implies that u 1 is 1. It follows that u actually lies in ![]() $\Gamma(G\times X, \mathcal{O}_{G\times X}^\times)$. Now, the desired group isomorphism follows from corollary 6.10.
$\Gamma(G\times X, \mathcal{O}_{G\times X}^\times)$. Now, the desired group isomorphism follows from corollary 6.10.
In the classical setting, a result of Rosenlicht states if X and Y are irreducible varieties, then every morphism ![]() $X \times Y \rightarrow GL_1$ is the product of a morphism
$X \times Y \rightarrow GL_1$ is the product of a morphism ![]() $X \rightarrow GL_1$ and a morphism
$X \rightarrow GL_1$ and a morphism ![]() $Y \rightarrow GL_1$ as shown in [Reference Brion7, Proposition 4.1.3] (Rosenlicht only proved a corollary (which is pretty different from what we are referencing)). The expository text [Reference Brion7] explains how this is used to study equivariant line bundles in the classical setting. We will prove an analogue for
$Y \rightarrow GL_1$ as shown in [Reference Brion7, Proposition 4.1.3] (Rosenlicht only proved a corollary (which is pretty different from what we are referencing)). The expository text [Reference Brion7] explains how this is used to study equivariant line bundles in the classical setting. We will prove an analogue for ![]() $\mathbb{F}_1$-schemes.
$\mathbb{F}_1$-schemes.
Lemma 6.13. Let ![]() $X, Y$ be
$X, Y$ be ![]() $\mathbb{F}_1$-schemes that are either affine or irreducible. Let
$\mathbb{F}_1$-schemes that are either affine or irreducible. Let ![]() $u \in \Gamma(X \times Y, \mathcal{O}_{X\times Y}^\times)$. Then there exists unique
$u \in \Gamma(X \times Y, \mathcal{O}_{X\times Y}^\times)$. Then there exists unique ![]() $\alpha \in \Gamma(X, \mathcal{O}_X^\times)$ and
$\alpha \in \Gamma(X, \mathcal{O}_X^\times)$ and ![]() $\beta \in \Gamma(Y, \mathcal{O}_Y^\times)$ such that
$\beta \in \Gamma(Y, \mathcal{O}_Y^\times)$ such that ![]() $u = \alpha\beta$.
$u = \alpha\beta$.
Proof. We consider first the case where ![]() $X = \operatorname{Spec} A$ and
$X = \operatorname{Spec} A$ and ![]() $Y = \operatorname{Spec} B$ are affine. As a monoid,
$Y = \operatorname{Spec} B$ are affine. As a monoid, ![]() $A \otimes_{\mathbb{F}_1} B$ is obtained from the (unpointed) monoid A × B by identifying
$A \otimes_{\mathbb{F}_1} B$ is obtained from the (unpointed) monoid A × B by identifying ![]() $(0, b)$ and
$(0, b)$ and ![]() $(a, 0)$ with
$(a, 0)$ with ![]() $(0, 0)$ for all
$(0, 0)$ for all ![]() $a \in A$ and
$a \in A$ and ![]() $b \in B$; this is an
$b \in B$; this is an ![]() $\mathbb{F}_1$-algebra with zero element
$\mathbb{F}_1$-algebra with zero element ![]() $(0, 0)$. The quotient map
$(0, 0)$. The quotient map ![]() $\pi:A \times B \to (A\otimes_{\mathbb{F}_1}B)$ gives rise to a map
$\pi:A \times B \to (A\otimes_{\mathbb{F}_1}B)$ gives rise to a map
We claim that θ is bijective. In fact, θ is injective because the only fibre of the quotient map π containing more than one element is ![]() $A\times \{0\} \cup \{0\} \times B$, and this fibre contains no units. Surjectivity is similar: if
$A\times \{0\} \cup \{0\} \times B$, and this fibre contains no units. Surjectivity is similar: if ![]() $x \in (A \otimes_{\mathbb{F}_1} B)^\times$ then we can let y be the unique element of
$x \in (A \otimes_{\mathbb{F}_1} B)^\times$ then we can let y be the unique element of ![]() $\pi^{-1}(x)$ and z be the unique element of
$\pi^{-1}(x)$ and z be the unique element of ![]() $\pi^{-1}(x^{-1})$ and observe that
$\pi^{-1}(x^{-1})$ and observe that ![]() $\pi(yz) = 1$. Since the fibre over 1 contains a single element, yz = 1 so
$\pi(yz) = 1$. Since the fibre over 1 contains a single element, yz = 1 so ![]() $x = \pi(y)$ for some unit y and
$x = \pi(y)$ for some unit y and ![]() $x \in \mathrm{im} \theta$. Thus, θ is bijective. Since we can view
$x \in \mathrm{im} \theta$. Thus, θ is bijective. Since we can view ![]() $\pi: A \times B \rightarrow (A \otimes_{\mathbb{F}_1} B)$ as the multiplication map, θ is the multiplication map on units, which establishes the result in the affine case.
$\pi: A \times B \rightarrow (A \otimes_{\mathbb{F}_1} B)$ as the multiplication map, θ is the multiplication map on units, which establishes the result in the affine case.
Next, suppose Y is such that the result holds for any pair (Z, Y) with Z affine. Suppose X is irreducible. Let ![]() $U \subseteq X$ be open affine. Then by the affine case, for
$U \subseteq X$ be open affine. Then by the affine case, for ![]() $u \in \Gamma(X\times Y, \mathcal{O}_{X\times Y}^\times)$, there exists unique elements
$u \in \Gamma(X\times Y, \mathcal{O}_{X\times Y}^\times)$, there exists unique elements ![]() $\alpha_U \in \Gamma(U, \mathcal{O}_X^\times)$ and
$\alpha_U \in \Gamma(U, \mathcal{O}_X^\times)$ and ![]() $\beta_U \in \Gamma(Y, \mathcal{O}_Y^\times)$ such that
$\beta_U \in \Gamma(Y, \mathcal{O}_Y^\times)$ such that
Let ![]() $U_1, U_2$ be open affine subsets of X; they are nondisjoint by irreducibility. Let
$U_1, U_2$ be open affine subsets of X; they are nondisjoint by irreducibility. Let ![]() $V \subseteq U_1 \cap U_2$ be a nonempty open affine subset. Then restricting the factorization of
$V \subseteq U_1 \cap U_2$ be a nonempty open affine subset. Then restricting the factorization of ![]() $u\mid_{U_1\times Y}$ to V × Y gives
$u\mid_{U_1\times Y}$ to V × Y gives
By applying the argument to U 2 and using uniqueness of ![]() $\alpha_V, \beta_V$, we obtain
$\alpha_V, \beta_V$, we obtain
Since βU does depend on U, we denote it β. Fix the open cover ![]() $\{U_i \}$ of X containing all open affine sets. We have seen that the sections
$\{U_i \}$ of X containing all open affine sets. We have seen that the sections ![]() $\alpha_{U_i}\in \Gamma(U_i, \mathcal{O}_X^\times)$ agree on overlaps, so give rise to
$\alpha_{U_i}\in \Gamma(U_i, \mathcal{O}_X^\times)$ agree on overlaps, so give rise to ![]() $\alpha \in \Gamma(X, \mathcal{O}_X^\times)$.
$\alpha \in \Gamma(X, \mathcal{O}_X^\times)$.
We now must show α and β are the unique elements of ![]() $\Gamma(X, \mathcal{O}_X^\times)$ and
$\Gamma(X, \mathcal{O}_X^\times)$ and ![]() $\Gamma(Y, \mathcal{O}_Y^\times)$ such that
$\Gamma(Y, \mathcal{O}_Y^\times)$ such that ![]() $u = \alpha \beta$. For any open affine
$u = \alpha \beta$. For any open affine ![]() $U\subseteq X$, we have
$U\subseteq X$, we have
. Since the sets U × Y where U ranges over open affine sets forms a cover of X × Y, ![]() $u = \alpha\beta$. If
$u = \alpha\beta$. If ![]() $u = \alpha' \beta'$ then restricting to U × Y gives
$u = \alpha' \beta'$ then restricting to U × Y gives ![]() $\alpha'\mid_U \beta' = u\mid_{U\times Y} = \alpha\mid_U \beta$. By the uniqueness of
$\alpha'\mid_U \beta' = u\mid_{U\times Y} = \alpha\mid_U \beta$. By the uniqueness of ![]() $\alpha_U, \beta_U$, we obtain
$\alpha_U, \beta_U$, we obtain ![]() $\beta' = \beta$ and
$\beta' = \beta$ and ![]() $\alpha'\mid_U = \alpha\mid_U$. Since α and
$\alpha'\mid_U = \alpha\mid_U$. Since α and ![]() $\alpha'$ agree on all open affine subsets, they are equal.
$\alpha'$ agree on all open affine subsets, they are equal.
This establishes the result when X is irreducible and Y is such that the result holds for all pairs (Z, Y) with Z affine. Since we have proven the affine case, any affine ![]() $\mathbb{F}_1$-scheme Y satisfies this hypothesis; hence the result holds when X is irreducible and Y is affine or by symmetry when X is affine and Y is irreducible. This implies any irreducible scheme Y satisfies the above hypothesis, so the result holds when X and Y are irreducible.
$\mathbb{F}_1$-scheme Y satisfies this hypothesis; hence the result holds when X is irreducible and Y is affine or by symmetry when X is affine and Y is irreducible. This implies any irreducible scheme Y satisfies the above hypothesis, so the result holds when X and Y are irreducible.
In the ![]() $\mathbb{F}_1$-setting, the above can be used to relate equivariant line bundles to characters of G. We remark that using proposition 6.12, we can also apply proposition 6.15 to the semiring case. We will need the following lemma.
$\mathbb{F}_1$-setting, the above can be used to relate equivariant line bundles to characters of G. We remark that using proposition 6.12, we can also apply proposition 6.15 to the semiring case. We will need the following lemma.
Lemma 6.14. Let X be a scheme over ![]() $\mathbb{F}_1$ and
$\mathbb{F}_1$ and ![]() $f:X \to \text{GL}_1$ be a morphism of
$f:X \to \text{GL}_1$ be a morphism of ![]() $\mathbb{F}_1$-schemes. If
$\mathbb{F}_1$-schemes. If ![]() $f_A(x)$ does not depend on
$f_A(x)$ does not depend on ![]() $x \in X(A)$ for any A, then
$x \in X(A)$ for any A, then ![]() $f_A(x) = 1$ for all
$f_A(x) = 1$ for all ![]() $x \in X(A)$.
$x \in X(A)$.
Proof. The constancy of fA implies it factors through the terminal map (as a set map)
yielding a map  $\hat{f}_A: (\operatorname{Spec} \mathbb{F}_1)(A) \rightarrow \text{GL}_1(A)$.
$\hat{f}_A: (\operatorname{Spec} \mathbb{F}_1)(A) \rightarrow \text{GL}_1(A)$.
We claim that ![]() $\hat{f}$ is natural in A. In fact, let
$\hat{f}$ is natural in A. In fact, let ![]() $\psi:\operatorname{Spec} B \to \operatorname{Spec} A$, and
$\psi:\operatorname{Spec} B \to \operatorname{Spec} A$, and ![]() $\psi_i^*$ be the induced maps on X,
$\psi_i^*$ be the induced maps on X, ![]() $\operatorname{Spec} \mathbb{F}_1$, and
$\operatorname{Spec} \mathbb{F}_1$, and ![]() $\text{GL}_1$. Consider the following diagram:
$\text{GL}_1$. Consider the following diagram:

The whole square and the left square commute by the definition of t and f, i.e.,
 \begin{equation*}
\psi_3^*\hat{f}_At_A=\hat{f}_Bt_B\psi_1^* \textrm{and } \psi_2^*t_A=t_B\psi_1^*.
\end{equation*}
\begin{equation*}
\psi_3^*\hat{f}_At_A=\hat{f}_Bt_B\psi_1^* \textrm{and } \psi_2^*t_A=t_B\psi_1^*.
\end{equation*}Hence we have
 \begin{equation*}
\psi_3^*\hat{f}_At_A=\hat{f}_B\psi_2^*t_A.
\end{equation*}
\begin{equation*}
\psi_3^*\hat{f}_At_A=\hat{f}_B\psi_2^*t_A.
\end{equation*}But, since tA is surjective, we have
 \begin{equation*}
\psi_3^*\hat{f}_A=\hat{f}_B\psi_2^*,
\end{equation*}
\begin{equation*}
\psi_3^*\hat{f}_A=\hat{f}_B\psi_2^*,
\end{equation*} which is precisely the naturality for ![]() $\hat{f}$. Hence, we obtain a morphism
$\hat{f}$. Hence, we obtain a morphism ![]() $\hat{f}: \operatorname{Spec} \mathbb{F}_1 \rightarrow GL_1$. But
$\hat{f}: \operatorname{Spec} \mathbb{F}_1 \rightarrow GL_1$. But ![]() $\mathbb{F}_1^\times $ has only the single element 1, so
$\mathbb{F}_1^\times $ has only the single element 1, so ![]() $\hat{f}_A$ is the constant map 1, and hence so is f.
$\hat{f}_A$ is the constant map 1, and hence so is f.
Proposition 6.15. Let G be a group scheme over ![]() $\mathbb{F}_1$ and X be an
$\mathbb{F}_1$ and X be an ![]() $\mathbb{F}_1$-scheme. Suppose G and X are either affine or irreducible. Then there is a group isomorphism between
$\mathbb{F}_1$-scheme. Suppose G and X are either affine or irreducible. Then there is a group isomorphism between
and
This correspondence is characterized by the property that G acts on the element 1x of the fibre over X(A) via ![]() $g 1_x = \chi_A(g) 1_{gx}$.
$g 1_x = \chi_A(g) 1_{gx}$.
Proof. By proposition 6.8, it suffices to construct a group isomorphism between homomorphisms ![]() $G \rightarrow \text{GL}_1$ and principal maps
$G \rightarrow \text{GL}_1$ and principal maps ![]() $u: G \times X \rightarrow \text{GL}_1$ (as in definition 6.6). In other words,
$u: G \times X \rightarrow \text{GL}_1$ (as in definition 6.6). In other words,
for all ![]() $\mathbb{F}_1$-algebra A and all
$\mathbb{F}_1$-algebra A and all ![]() $(g, h, x) \in G(A) \times G(A) \times X(A)$.
$(g, h, x) \in G(A) \times G(A) \times X(A)$.
First, let u be a principal map. By lemmas 6.1 and 6.13, there exist unique ![]() $\alpha: G \rightarrow \text{GL}_1$ and
$\alpha: G \rightarrow \text{GL}_1$ and ![]() $\beta: X \rightarrow \text{GL}_1$ such that
$\beta: X \rightarrow \text{GL}_1$ such that ![]() $u_A(g, x) = \alpha_A(g) \beta_A(x)$ for all
$u_A(g, x) = \alpha_A(g) \beta_A(x)$ for all ![]() $(g, x)\in G(A) \times X(A)$. Then, we have
$(g, x)\in G(A) \times X(A)$. Then, we have
Since ![]() $\beta_A(x) \in \text{GL}_1(A)$ is invertible, we cancel it from both sides of (24) to obtain
$\beta_A(x) \in \text{GL}_1(A)$ is invertible, we cancel it from both sides of (24) to obtain
Since the image of αA consists of units, this equation gives
 \begin{equation}
\beta_A(hx) = \frac{\alpha_A(gh)}{\alpha_A(g)\alpha_A(h)}.
\end{equation}
\begin{equation}
\beta_A(hx) = \frac{\alpha_A(gh)}{\alpha_A(g)\alpha_A(h)}.
\end{equation} By taking h = 1 in the above, we obtain ![]() $\beta_A(x) = \alpha_A(1)^{-1}$, so βA is constant. By lemma 6.14,
$\beta_A(x) = \alpha_A(1)^{-1}$, so βA is constant. By lemma 6.14, ![]() $\beta_A(x) = 1$ for all x. Then, from (25), we have
$\beta_A(x) = 1$ for all x. Then, from (25), we have
showing that α is a homomorphism.
Thus we have constructed a map from principal maps u to the set of homomorphisms ![]() $\alpha: G \rightarrow GL_1$. Moreover, the equation
$\alpha: G \rightarrow GL_1$. Moreover, the equation ![]() $u_A(g, x) = \alpha_A(g) \beta_A(x) = \alpha_A(g)$ implies u is determined by α, i.e., the map is injective.
$u_A(g, x) = \alpha_A(g) \beta_A(x) = \alpha_A(g)$ implies u is determined by α, i.e., the map is injective.
For surjectivity, fix a homomorphism ![]() $\alpha: G \rightarrow GL_1$ and define u by
$\alpha: G \rightarrow GL_1$ and define u by ![]() $u_A(g, x) = \alpha_A(g)$, i.e., u is the composition
$u_A(g, x) = \alpha_A(g)$, i.e., u is the composition ![]() $\alpha \circ \pi: G \times X \rightarrow G \rightarrow GL_1$. Then, we have
$\alpha \circ \pi: G \times X \rightarrow G \rightarrow GL_1$. Then, we have
which establishes surjectivity.
Because the correspondence we are considering is given by ![]() $u_A(g, x) = \alpha_A(g)$, we show it is a homomorphism as follows. Let
$u_A(g, x) = \alpha_A(g)$, we show it is a homomorphism as follows. Let ![]() $\alpha, \alpha'$ correspond to
$\alpha, \alpha'$ correspond to ![]() $u, u'$. Then, we have
$u, u'$. Then, we have
and hence uu ʹ corresponds to ![]() $\alpha\alpha'$.
$\alpha\alpha'$.
Finally, by proposition 6.8, the equivariant line bundle is characterized by the property that G acts on 1x via ![]() $g1_x = u_A(g, x)1_{gx} = \alpha(g) 1_{gx}$.
$g1_x = u_A(g, x)1_{gx} = \alpha(g) 1_{gx}$.
Note that two different equivariant structures on the line bundle ![]() $\mathcal{O}_X$ may be isomorphic under an automorphism of the line bundle. Our next goal is to determine which equivariant structures are isomorphic.
$\mathcal{O}_X$ may be isomorphic under an automorphism of the line bundle. Our next goal is to determine which equivariant structures are isomorphic.
A first step towards this goal is the following easy lemma.
Lemma 6.16. Let K be either a semiring or a monoid. Let X be a scheme over K and G be a group scheme over K acting on X. Fix a morphism ![]() $f: X \rightarrow GL_1$. Let u be the ratio of the two morphisms
$f: X \rightarrow GL_1$. Let u be the ratio of the two morphisms ![]() $G\times X \rightarrow GL_1$ obtained by composing f with either the action or the projection
$G\times X \rightarrow GL_1$ obtained by composing f with either the action or the projection ![]() $G\times X \rightarrow X$. In other words, the functor of points of u is given by
$G\times X \rightarrow X$. In other words, the functor of points of u is given by
Then u is principal, i.e., u satisfies ![]() $u_A(gh, x) = u_A(h, x) u_A(g, hx)$.
$u_A(gh, x) = u_A(h, x) u_A(g, hx)$.
In what follows, let K be either a semiring or a monoid, X be a scheme over K and G be a group scheme over K acting on X unless otherwise stated.
Lemma 6.17. Let L and L ʹ be two equivariant line bundles whose underlying line bundle is ![]() $\mathcal{O}_X$ and let
$\mathcal{O}_X$ and let ![]() $u, u': G\times X \to \text{GL}_1$ be the associated principal maps from the construction of lemma 6.8. Then
$u, u': G\times X \to \text{GL}_1$ be the associated principal maps from the construction of lemma 6.8. Then ![]() $L \simeq L'$ as equivariant line bundles if and only if there is some
$L \simeq L'$ as equivariant line bundles if and only if there is some ![]() $f: X \rightarrow \text{GL}_1$ such that
$f: X \rightarrow \text{GL}_1$ such that
for all K-algebra A and all ![]() $(g, x)\in G(A) \times X(A)$.
$(g, x)\in G(A) \times X(A)$.
Proof. Let v be a basis element of L and w be a basis element of L ʹ (for concreteness, we take both to be ![]() $1\in \Gamma(X, \mathcal{O}_X^\times)$, but giving them individual names makes the argument more clear). Given an isomorphism
$1\in \Gamma(X, \mathcal{O}_X^\times)$, but giving them individual names makes the argument more clear). Given an isomorphism ![]() $\phi: L \rightarrow L'$, we obtain a basis element
$\phi: L \rightarrow L'$, we obtain a basis element ![]() $\phi(v)$ of L ʹ. Such a basis element must have the form
$\phi(v)$ of L ʹ. Such a basis element must have the form ![]() $\phi(v) = \alpha w$ for some
$\phi(v) = \alpha w$ for some ![]() $\alpha \in \Gamma(X, \mathcal{O}_X^\times)$. Let
$\alpha \in \Gamma(X, \mathcal{O}_X^\times)$. Let ![]() $f: X\rightarrow GL_1$ corresponds to α under lemma 6.1. For
$f: X\rightarrow GL_1$ corresponds to α under lemma 6.1. For ![]() $x\in X(A)$, the naturality part of lemma 6.1 tells us that
$x\in X(A)$, the naturality part of lemma 6.1 tells us that ![]() $f_A(x) = f \circ x$ corresponds to
$f_A(x) = f \circ x$ corresponds to ![]() $x^*(\alpha) \in GL_1(A)$. So, we identify
$x^*(\alpha) \in GL_1(A)$. So, we identify ![]() $x^*(\alpha)$ with
$x^*(\alpha)$ with ![]() $f_A(x)$.
$f_A(x)$.
G(A) acts on the fibre ![]() $L'_x$ via
$L'_x$ via ![]() $g(w_x) = u'_A(g, x) w_{gx}$. So, we have
$g(w_x) = u'_A(g, x) w_{gx}$. So, we have
On the other hand, since ϕ is an isomorphism of equivariant bundles,
Combining the two equations yields Eq. (27) as desired.
Conversely, suppose we are given ![]() $f: X \rightarrow GL_1$ satisfying (27). f corresponds to a unit
$f: X \rightarrow GL_1$ satisfying (27). f corresponds to a unit ![]() $f \in \Gamma(X, \mathcal{O}_X^\times)$, and we obtain a basis vector
$f \in \Gamma(X, \mathcal{O}_X^\times)$, and we obtain a basis vector ![]() $\eta \in \Gamma(X, L')$ by multiplying w with f. For each K-algebra A and each
$\eta \in \Gamma(X, L')$ by multiplying w with f. For each K-algebra A and each ![]() $x\in X(A)$, define
$x\in X(A)$, define ![]() $\phi_x: L_x \rightarrow L'_x$ via
$\phi_x: L_x \rightarrow L'_x$ via
for all ![]() $a\in A$. Combining the maps on different fibres gives rise to maps
$a\in A$. Combining the maps on different fibres gives rise to maps
compatible with the projections of each bundle onto X(A). It remains to show ϕ is an isomorphism of equivariant line bundles. We have seen compatibility with projections, and the fact that ϕx is a linear isomorphism for each point x is clear.
Next we check that ϕ is equivariant. By the same calculations as the other direction of this proof, ![]() $g(\phi_A(v_x)) = f_A(x) u'_A(g, x) w_{gx}$ and
$g(\phi_A(v_x)) = f_A(x) u'_A(g, x) w_{gx}$ and ![]() $\phi_A(g v_x) = u_A(g, x) f_A(gx) w_{gx}$. Combining with (27), we see that
$\phi_A(g v_x) = u_A(g, x) f_A(gx) w_{gx}$. Combining with (27), we see that ![]() $g \circ \phi_x$ and
$g \circ \phi_x$ and ![]() $\phi_{gx} \circ g$ agree on a basis vector, and hence are equal, which implies
$\phi_{gx} \circ g$ agree on a basis vector, and hence are equal, which implies ![]() $g \circ \phi_A = \phi_A \circ g$.
$g \circ \phi_A = \phi_A \circ g$.
Finally, we show that ϕ is natural in A. To show that the action is natural in A, let ![]() $h:\operatorname{Spec} B \to \operatorname{Spec} A$, and
$h:\operatorname{Spec} B \to \operatorname{Spec} A$, and ![]() $h^*$ be the induced maps. We need to show that the following diagram commutes:
$h^*$ be the induced maps. We need to show that the following diagram commutes:

Let ![]() $av_x \in L_x \subseteq L(A)$. Then we have
$av_x \in L_x \subseteq L(A)$. Then we have
and
From the naturality of f, we have ![]() $h^*f_A = f_Bh^*$, it follows that we have
$h^*f_A = f_Bh^*$, it follows that we have
showing that ϕ is natural in A.
Proposition 6.18. Let X be a toric ![]() $\mathbb{F}_1$-scheme and G be a group scheme over
$\mathbb{F}_1$-scheme and G be a group scheme over ![]() $\mathbb{F}_1$. Let K be an idempotent semifield. Suppose G × X is connected. Then there is a one-to-one correspondence between isomorphism classes of GK-equivariant line bundles on XK which are trivial as line bundles and isomorphism classes of G-equivariant line bundles on X which are trivial as line bundles.
$\mathbb{F}_1$. Let K be an idempotent semifield. Suppose G × X is connected. Then there is a one-to-one correspondence between isomorphism classes of GK-equivariant line bundles on XK which are trivial as line bundles and isomorphism classes of G-equivariant line bundles on X which are trivial as line bundles.
Proof. From proposition 6.12, we have a one-to-one correspondence between G-equivariant line bundle structures on ![]() $\mathcal{O}_X$ and GK-equivariant line bundle structures on
$\mathcal{O}_X$ and GK-equivariant line bundle structures on ![]() $\mathcal{O}_{X_K}$. Now, with the same notation as in lemma 6.17, two equivariant structures for the trivial line bundle on X are isomorphic over
$\mathcal{O}_{X_K}$. Now, with the same notation as in lemma 6.17, two equivariant structures for the trivial line bundle on X are isomorphic over ![]() $X_{\mathbb{T}}$ if and only if the ratio of the corresponding units has the form
$X_{\mathbb{T}}$ if and only if the ratio of the corresponding units has the form ![]() $f(gx) / f(x)$. But a constant factor in front of f does not affect this expression, so we may assume that f has no component in
$f(gx) / f(x)$. But a constant factor in front of f does not affect this expression, so we may assume that f has no component in ![]() $K^\times$, so it also yields an isomorphism of equivariant line bundles over X from proposition 6.12.
$K^\times$, so it also yields an isomorphism of equivariant line bundles over X from proposition 6.12.
7. Gluing equivariant vector bundles
It would be useful to be able to restrict equivariant vector bundles on X to open sets ![]() $U\subseteq X$. This is not always possible: if U is not closed under the G-action, it should not inherit a G-action, so the notion of an equivariant vector bundle on U does not even make sense. The next lemma shows that this is the only obstruction.
$U\subseteq X$. This is not always possible: if U is not closed under the G-action, it should not inherit a G-action, so the notion of an equivariant vector bundle on U does not even make sense. The next lemma shows that this is the only obstruction.
Let R be a semiring or monoid. Let G be a group scheme over R. Let X be a scheme over R equipped with a G-action. Let E be a G-equivariant vector bundle on X. Let ![]() $U\subseteq X$ be an open set with the property that the action
$U\subseteq X$ be an open set with the property that the action ![]() $G \times_R X \rightarrow X$ restricts to an action
$G \times_R X \rightarrow X$ restricts to an action ![]() $G \times_R U \rightarrow U$ and let
$G \times_R U \rightarrow U$ and let ![]() $i: U\rightarrow X$ be the inclusion. Let EU be the vector bundle obtained by restricting E to U. As in the previous section, for schemes X and Y over R, we will simply write X × Y instead of
$i: U\rightarrow X$ be the inclusion. Let EU be the vector bundle obtained by restricting E to U. As in the previous section, for schemes X and Y over R, we will simply write X × Y instead of ![]() $X\times_RY$ when there is no possible confusion.
$X\times_RY$ when there is no possible confusion.
Lemma 7.1. With the same notation as above, the following hold.
(1) For any R-algebra A and any
 $u \in U(A)$, the fibre of EU over u is equal to the fibre of E over i(u).
$u \in U(A)$, the fibre of EU over u is equal to the fibre of E over i(u).(2) There is a unique equivariant vector bundle structure on EU such that for each
 $(g, u) \in G(A) \times U(A)$, the induced map on fibres
$(g, u) \in G(A) \times U(A)$, the induced map on fibres  $g: (E_U)_u \rightarrow (E_U)_{gu}$ is the same as the map
$g: (E_U)_u \rightarrow (E_U)_{gu}$ is the same as the map  $g: E_{i(u)} \rightarrow E_{g i(u)}$ induced by the equivariant structure on E.
$g: E_{i(u)} \rightarrow E_{g i(u)}$ induced by the equivariant structure on E.
Proof. (1) EU is the pullback of E along i. The fibre ![]() $(E_U)_u$ is the module of global sections of the pullback
$(E_U)_u$ is the module of global sections of the pullback ![]() $u^* E_U = u^* i^* E$. Since
$u^* E_U = u^* i^* E$. Since ![]() $i(u) = i \circ u$,
$i(u) = i \circ u$, ![]() $(E_U)_u$ equals the module of global sections of
$(E_U)_u$ equals the module of global sections of ![]() $i(u)^* E$, and this module is
$i(u)^* E$, and this module is ![]() $E_{i(u)}$.
$E_{i(u)}$.
(2) The action map ![]() $\rho_A^U:G(A) \times E_U(A) \rightarrow E_U(A)$ is determined by how G(A) acts on each fibre, and this is specified in the statement of the lemma. To show this is an action, we must show that for any
$\rho_A^U:G(A) \times E_U(A) \rightarrow E_U(A)$ is determined by how G(A) acts on each fibre, and this is specified in the statement of the lemma. To show this is an action, we must show that for any ![]() $v \in (E_U)_u$ and
$v \in (E_U)_u$ and ![]() $g, h \in G(A)$,
$g, h \in G(A)$, ![]() $(gh)v = g(hv)$. But this is true because by construction G acts on the fibre in the same way if we view it as
$(gh)v = g(hv)$. But this is true because by construction G acts on the fibre in the same way if we view it as ![]() $E_{i(u)}$, and the map
$E_{i(u)}$, and the map ![]() $\rho_A:G(A) \times E(A) \rightarrow E(A)$ really is a group action. The action map induces linear isomorphisms on fibres, since fibrewise it looks the same as the action on E.
$\rho_A:G(A) \times E(A) \rightarrow E(A)$ really is a group action. The action map induces linear isomorphisms on fibres, since fibrewise it looks the same as the action on E.
It remains to check naturality. Let ![]() $f:\operatorname{Spec} B \to \operatorname{Spec} A$, and
$f:\operatorname{Spec} B \to \operatorname{Spec} A$, and ![]() $f^*$ be the induced maps. We need to show that the following diagram commutes:
$f^*$ be the induced maps. We need to show that the following diagram commutes:

But, under the inclusion i, we may view ![]() $E_U(A)$ as a subset of E(A) and
$E_U(A)$ as a subset of E(A) and ![]() $\rho_A^U=\rho_A\mid_U$. In particular, the naturality directly follows from that of ρ.
$\rho_A^U=\rho_A\mid_U$. In particular, the naturality directly follows from that of ρ.
The following proposition shows that under suitable conditions, we may obtain equivariant vector bundles from gluing equivariant vector bundles on an open cover.
Let R be a semiring or monoid. Let G be a group scheme over R. Let G be a group scheme over R, let X be a scheme over R equipped with a G-action, and let E be a vector bundle over X. Let ![]() $\{U_i \}$ be an open cover of X and suppose each open set Ui is G-invariant in the sense that the action on X restricts to maps
$\{U_i \}$ be an open cover of X and suppose each open set Ui is G-invariant in the sense that the action on X restricts to maps ![]() $G \times U_i \rightarrow U_i$.
$G \times U_i \rightarrow U_i$.
Proposition 7.2. With the same notation as above, there is a one-to-one correspondence between equivariant structures on E and collections of equivariant structures on each ![]() $E_{U_i}$ with the property that restricting the action from
$E_{U_i}$ with the property that restricting the action from ![]() $E_{U_i}$ or
$E_{U_i}$ or ![]() $E_{U_j}$ to
$E_{U_j}$ to ![]() $E_{U_{ij}}$ yield the same morphism
$E_{U_{ij}}$ yield the same morphism ![]() $G \times E_{U_{ij}} \rightarrow E_{U_{ij}}$, where
$G \times E_{U_{ij}} \rightarrow E_{U_{ij}}$, where ![]() $E_{U_{ij}}:=E_{U_i} \cap E_{U_j}$.
$E_{U_{ij}}:=E_{U_i} \cap E_{U_j}$.
Proof. We first prove the semiring case. We will use the geometric vector bundle perspective to view E as a scheme equipped with a map ![]() $\pi: E \rightarrow X$. From the definition, one can easily see that EU is an open subscheme of E for a G-invariant open subset U.
$\pi: E \rightarrow X$. From the definition, one can easily see that EU is an open subscheme of E for a G-invariant open subset U.
If E is an equivariant vector bundle, we can give a geometric description of the action on the bundle EU from lemma 7.1. It is clear that the functor of points for the action on EU is exactly the same as the functor of points from the map ![]() $G \times E_{U} \rightarrow E_{U}$ whose composition with the open immersion
$G \times E_{U} \rightarrow E_{U}$ whose composition with the open immersion ![]() $E_{U}\rightarrow E$ is the restriction
$E_{U}\rightarrow E$ is the restriction ![]() $G \times E_{U} \rightarrow E$ of the action because both are given by
$G \times E_{U} \rightarrow E$ of the action because both are given by ![]() $g, v \mapsto \beta(g, v)$, where β is the action on E, and where we identify U(A) with a subset of X(A). In other words, the equivariant vector bundle structure on EU is the same one that is obtained by restriction of the action viewed as a morphism of schemes.
$g, v \mapsto \beta(g, v)$, where β is the action on E, and where we identify U(A) with a subset of X(A). In other words, the equivariant vector bundle structure on EU is the same one that is obtained by restriction of the action viewed as a morphism of schemes.
Suppose we are given actions ![]() $\beta_i: G \times E_{U_i} \rightarrow E_{U_i}$ which agree on overlaps and which make each
$\beta_i: G \times E_{U_i} \rightarrow E_{U_i}$ which agree on overlaps and which make each ![]() $E_{U_i}$ into an equivariant vector bundle. Then we may glue them to obtain a map
$E_{U_i}$ into an equivariant vector bundle. Then we may glue them to obtain a map ![]() $\beta: G \times E \rightarrow E$. Since each βi is compatible with the action
$\beta: G \times E \rightarrow E$. Since each βi is compatible with the action ![]() $\alpha_{U_i}: G \times U_i \rightarrow U_i$, β must be compatible with
$\alpha_{U_i}: G \times U_i \rightarrow U_i$, β must be compatible with ![]() $\alpha: G\times X \rightarrow X$. Consider the maps
$\alpha: G\times X \rightarrow X$. Consider the maps
given on functors of points by
Consider maps ![]() $\eta_i, \theta_i$ defined similarly using the actions on
$\eta_i, \theta_i$ defined similarly using the actions on ![]() $E_{U_i}$. Since βi is an action, we obtain
$E_{U_i}$. Since βi is an action, we obtain ![]() $\eta_i = \theta_i$. Clearly if
$\eta_i = \theta_i$. Clearly if ![]() $v \in E_{U_i}(A)$ and
$v \in E_{U_i}(A)$ and ![]() $g, h \in G(A)$ then
$g, h \in G(A)$ then ![]() $\eta(g, h, v) = \eta_i(g, h, v)$ and similarly for θ, and hence
$\eta(g, h, v) = \eta_i(g, h, v)$ and similarly for θ, and hence ![]() $\eta = \theta$, showing that β is a group action.
$\eta = \theta$, showing that β is a group action.
Consider the map ![]() $+: E \times E \rightarrow E$ which is simply vector addition on the level of functors of points. From proposition 3.20, + is a morphism of schemes when we view E as a geometric vector bundle. To show that β is additive on fibres we need to show for
$+: E \times E \rightarrow E$ which is simply vector addition on the level of functors of points. From proposition 3.20, + is a morphism of schemes when we view E as a geometric vector bundle. To show that β is additive on fibres we need to show for ![]() $g \in G(A)$,
$g \in G(A)$, ![]() $x \in X(A)$ and
$x \in X(A)$ and ![]() $v, w \in E_x$ that
$v, w \in E_x$ that ![]() $\beta(g, v + w) = \beta(g, v) + \beta(g, w)$. We may rephrase this as
$\beta(g, v + w) = \beta(g, v) + \beta(g, w)$. We may rephrase this as
where ![]() $\Delta: G \to G \times G$ is the diagonal and
$\Delta: G \to G \times G$ is the diagonal and ![]() $\varphi:G\times G \times E \times E \to G\times E \times G \times E$ switches the second and the third coordinates. In view of the assumptions on the open cover, it suffices to check that the additivity holds on each
$\varphi:G\times G \times E \times E \to G\times E \times G \times E$ switches the second and the third coordinates. In view of the assumptions on the open cover, it suffices to check that the additivity holds on each ![]() $E_{U_i}$ and by retracing our steps, this is equivalent to βi being additive on fibres. Since
$E_{U_i}$ and by retracing our steps, this is equivalent to βi being additive on fibres. Since ![]() $E_{U_i}$ is an equivariant vector bundle, β is additive on fibres. We may now show linearity on fibres by using the scalar multiplication map
$E_{U_i}$ is an equivariant vector bundle, β is additive on fibres. We may now show linearity on fibres by using the scalar multiplication map ![]() $\cdot: \mathbb{A}^1_X \times E \rightarrow E$, which is also a morphism of schemes when we view E as a geometric vector bundle from proposition 3.20.
$\cdot: \mathbb{A}^1_X \times E \rightarrow E$, which is also a morphism of schemes when we view E as a geometric vector bundle from proposition 3.20.
Finally, ![]() $\beta_A: G(A) \times X(A) \rightarrow X(A)$ is natural because it is a morphism of schemes. Thus E is an equivariant vector bundle.
$\beta_A: G(A) \times X(A) \rightarrow X(A)$ is natural because it is a morphism of schemes. Thus E is an equivariant vector bundle.
Conversely, suppose E is an equivariant vector bundle. Then we have seen that restricting the action ![]() $G \times E \rightarrow E$ to
$G \times E \rightarrow E$ to ![]() $E_{U_i}$ gives an equivariant vector bundle structure on
$E_{U_i}$ gives an equivariant vector bundle structure on ![]() $E_{U_i}$. Because these maps
$E_{U_i}$. Because these maps ![]() $\beta_i: G \times E_{U_i} \rightarrow E_{U_i}$ are all given by restricting a morphism of schemes, they must agree on overlaps.
$\beta_i: G \times E_{U_i} \rightarrow E_{U_i}$ are all given by restricting a morphism of schemes, they must agree on overlaps.
Now, one can easily see that this gives one-to-one correspondence.
For the monoid case, one may modify proposition 3.20 just for the scalar multiplication map since in this case one does not have an additive map. With this modification, the same proof goes through in this case.
We now show that in the toric case, all equivariant vector bundles are the sum of equivariant line bundles. This reduces the problem of classifying toric vector bundles to the line bundle case.
Definition 7.3. Let X be a scheme over a semiring R and G be a group scheme over R acting on X. Let E1 and E2 be G-equivariant line bundles. The direct sum ![]() $E=E_1\oplus E_2$ is a G-equivariant vector bundle whose underlying vector bundle is
$E=E_1\oplus E_2$ is a G-equivariant vector bundle whose underlying vector bundle is ![]() $E_1\oplus E_2$ (viewed E1 and E2 as vector bundles) and the action is given as follows:
$E_1\oplus E_2$ (viewed E1 and E2 as vector bundles) and the action is given as follows:
where ![]() $\beta_i:G\times E_i \to E_i$ is the action of Ei for
$\beta_i:G\times E_i \to E_i$ is the action of Ei for ![]() $i=1,2$. In other words, the action of E is componentwise.
$i=1,2$. In other words, the action of E is componentwise.
Theorem 7.4 7.4 Let X be a toric scheme over an idempotent semifield R, and let G be the corresponding torus. Let E be a G-equivariant vector bundle on X. Then there are unique (up to permutation) equivariant line bundles ![]() $L_1, \ldots, L_n$ such that
$L_1, \ldots, L_n$ such that ![]() $E = L_1 \oplus \ldots \oplus L_n$ (as G-equivariant vector bundles).
$E = L_1 \oplus \ldots \oplus L_n$ (as G-equivariant vector bundles).
Proof. First we prove uniqueness; the toric assumption is not needed here. By proposition 2.15, any direct sum decomposition of a vector bundle into line bundles is unique. So, we just need to show the action βi on each Li is determined by the action β on E. But by definition of a direct sum of equivariant line bundles, the action on ![]() $E = L_1 \oplus \ldots \oplus L_n$ is given by
$E = L_1 \oplus \ldots \oplus L_n$ is given by
In particular, for ![]() $v_i \in L_i$, βi is given by
$v_i \in L_i$, βi is given by ![]() $\beta_i(g, v_i) = \beta(g, v)$.
$\beta_i(g, v_i) = \beta(g, v)$.
As a vector bundle, again by proposition 2.15, E is a sum of line bundles. Call these line bundles ![]() $L_1, \ldots, L_n$. We need to specify the group action on the Li.
$L_1, \ldots, L_n$. We need to specify the group action on the Li.
For any cone σ, we let Eσ denote the restriction to Uσ and similarly for ![]() $(L_i)_{\sigma}$. Observe that
$(L_i)_{\sigma}$. Observe that
is the unique decomposition into line bundles (by proposition 2.15). Note Eσ is trivial by proposition 2.19. Furthermore, corollary 5.18 implies that Eσ is a sum of equivariant line bundles. By uniqueness of the decomposition into line bundles, these equivariant line bundles must equal ![]() $(L_1)_{\sigma}, \ldots, (L_n)_{\sigma}$. In other words, we have obtained equivariant line bundle structures on each
$(L_1)_{\sigma}, \ldots, (L_n)_{\sigma}$. In other words, we have obtained equivariant line bundle structures on each ![]() $(L_i)_{\sigma}$ such that
$(L_i)_{\sigma}$ such that ![]() $E_{\sigma} = (L_1)_{\sigma} \oplus\ldots\oplus (L_n)_{\sigma}$ as equivariant vector bundles.
$E_{\sigma} = (L_1)_{\sigma} \oplus\ldots\oplus (L_n)_{\sigma}$ as equivariant vector bundles.
Given two cones ![]() $\sigma_1, \sigma_2$, we let
$\sigma_1, \sigma_2$, we let ![]() $E_{\sigma_1, \sigma_2} = E_{U_{\sigma_1} \cap U_{\sigma_2}}$ and similarly for the Li. We obtain two equivariant vector bundle structures on each
$E_{\sigma_1, \sigma_2} = E_{U_{\sigma_1} \cap U_{\sigma_2}}$ and similarly for the Li. We obtain two equivariant vector bundle structures on each ![]() $(L_i)_{\sigma_1, \sigma_2}$ such that
$(L_i)_{\sigma_1, \sigma_2}$ such that ![]() $E_{\sigma_1, \sigma_2} = (L_1)_{\sigma_1, \sigma_2} \oplus\ldots\oplus (L_n)_{\sigma_1, \sigma_2}$: we can either restrict the action on
$E_{\sigma_1, \sigma_2} = (L_1)_{\sigma_1, \sigma_2} \oplus\ldots\oplus (L_n)_{\sigma_1, \sigma_2}$: we can either restrict the action on ![]() $(L_i)_{\sigma_1}$ or restrict the action on
$(L_i)_{\sigma_1}$ or restrict the action on ![]() $(L_i)_{\sigma_2}$. By the uniqueness part of the theorem (which does not really require
$(L_i)_{\sigma_2}$. By the uniqueness part of the theorem (which does not really require ![]() $U_{\sigma_1} \cap U_{\sigma_2}$ to be toric), these must give the same action on
$U_{\sigma_1} \cap U_{\sigma_2}$ to be toric), these must give the same action on ![]() $(L_i)_{\sigma_1, \sigma_2}$. Thus the actions on the
$(L_i)_{\sigma_1, \sigma_2}$. Thus the actions on the ![]() $(L_i)_{\sigma}$ for different values of σ agree on overlaps. By proposition 7.2, these glue together to give an action on Li.
$(L_i)_{\sigma}$ for different values of σ agree on overlaps. By proposition 7.2, these glue together to give an action on Li.
There are now two actions on E which make E into an equivariant vector bundle. The first is the action that comes from the assumption that E is a G-equivariant vector bundle. The other, we can obtain from the actions on the Li, which allow us to put an equivariant vector bundle structure on ![]() $E = L_1 \oplus \ldots \oplus L_n$. We had
$E = L_1 \oplus \ldots \oplus L_n$. We had ![]() $E_{\sigma} = (L_1)_{\sigma} \oplus\ldots\oplus (L_n)_{\sigma}$ as equivariant vector bundles. Hence the two actions on E agree when restricted to any Uσ. By proposition 7.2, this means the two actions are equal. The result now follows.
$E_{\sigma} = (L_1)_{\sigma} \oplus\ldots\oplus (L_n)_{\sigma}$ as equivariant vector bundles. Hence the two actions on E agree when restricted to any Uσ. By proposition 7.2, this means the two actions are equal. The result now follows.
Next we relate equivariant vector bundles on toric varieties to equivariant vector bundles on the torus. Conceptually this should use the density of the torus. But we need something stronger because it is not clear that regular functions that agree on a dense set should agree everywhere. In the classical case ![]() $\{x: f(x) = g(x) \}$ is closed as it is the set of prime ideals containing
$\{x: f(x) = g(x) \}$ is closed as it is the set of prime ideals containing ![]() $\langle f - g \rangle$, but in the tropical case we cannot use subtraction.
$\langle f - g \rangle$, but in the tropical case we cannot use subtraction.
Let X be a toric scheme over a semiring R. As in the case over ![]() $\mathbb{Z}$, one has
$\mathbb{Z}$, one has ![]() $X = \bigcup U_{\sigma_i}$, with each cone σi in a fan, and
$X = \bigcup U_{\sigma_i}$, with each cone σi in a fan, and ![]() $U_{\{0\}}\subseteq X$ is the torus.
$U_{\{0\}}\subseteq X$ is the torus.
Lemma 7.5. Let X be a toric scheme over a semiring R. Let ![]() $f, g \in \Gamma(X, \mathcal{O}_X)$. Suppose f = g on
$f, g \in \Gamma(X, \mathcal{O}_X)$. Suppose f = g on ![]() $U_{\{0\}}$. Then f = g.
$U_{\{0\}}$. Then f = g.
Proof. As a preliminary, observe that an injection of sets ![]() $S \rightarrow T$ induces an injection
$S \rightarrow T$ induces an injection ![]() $R^S \rightarrow R^T$ of free modules. In particular, an injection of monoids
$R^S \rightarrow R^T$ of free modules. In particular, an injection of monoids ![]() $M_1 \rightarrow M_2$ induces a monomorphism
$M_1 \rightarrow M_2$ induces a monomorphism ![]() $R[M_1] \rightarrow R[M_2]$.
$R[M_1] \rightarrow R[M_2]$.
First consider the case where X is an affine scheme, corresponding to a cone σ, i.e., ![]() $X = \operatorname{Spec} R[\Lambda \cap \sigma^\vee]$ for some lattice Λ and some cone σ. The torus is
$X = \operatorname{Spec} R[\Lambda \cap \sigma^\vee]$ for some lattice Λ and some cone σ. The torus is ![]() $\operatorname{Spec} R[\Lambda]$. Because the inclusion
$\operatorname{Spec} R[\Lambda]$. Because the inclusion ![]() $\Lambda \cap \sigma^\vee$ into Λ is injective, the map
$\Lambda \cap \sigma^\vee$ into Λ is injective, the map ![]() $\phi: R[\Lambda \cap \sigma^\vee] \rightarrow R[\Lambda]$ is a monomorphism. Consider two regular functions
$\phi: R[\Lambda \cap \sigma^\vee] \rightarrow R[\Lambda]$ is a monomorphism. Consider two regular functions ![]() $f, g$ on X which agree on the torus. Algebraically, this means
$f, g$ on X which agree on the torus. Algebraically, this means ![]() $\phi(f) = \phi(g)$, and injectivity gives f = g as desired.
$\phi(f) = \phi(g)$, and injectivity gives f = g as desired.
Now we consider the general case. Assume f = g on the torus. For each cone σ in the fan corresponding to X, we may apply this result to Uσ to obtain ![]() $f \mid_{U_{\sigma}} = g \mid_{U_{\sigma}}$. Since the Uσ form an open cover, the result follows.
$f \mid_{U_{\sigma}} = g \mid_{U_{\sigma}}$. Since the Uσ form an open cover, the result follows.
We may view regular functions as sections of the trivial line bundle. In fact, the above result can be generalized to any vector bundle.
Lemma 7.6. Let X be a toric scheme over an idempotent semifield R. Let E be a vector bundle on X. Suppose ![]() $s, t \in \Gamma(X, E)$ are such that
$s, t \in \Gamma(X, E)$ are such that ![]() $s \mid_{U_{\{0\}}} = t \mid_{U_{\{0\}}}$. Then s = t.
$s \mid_{U_{\{0\}}} = t \mid_{U_{\{0\}}}$. Then s = t.
Proof. We have already proven in lemma 7.5 the statement when ![]() $E = \mathcal{O}_X$.
$E = \mathcal{O}_X$.
Next we consider the case where E is a line bundle. For any cone σ, ![]() $E_{U_{\sigma}}$ is trivial by proposition 2.19. Since
$E_{U_{\sigma}}$ is trivial by proposition 2.19. Since ![]() $s \mid_{U_{\sigma}}$ and
$s \mid_{U_{\sigma}}$ and ![]() $t \mid_{U_{\sigma}}$ agree on the torus, they are equal by the case of the trivial line bundle. Since this holds for all σ and since E is a sheaf, we have s = t.
$t \mid_{U_{\sigma}}$ agree on the torus, they are equal by the case of the trivial line bundle. Since this holds for all σ and since E is a sheaf, we have s = t.
Finally, we use proposition 2.15 to write ![]() $E = L_1 \oplus \ldots \oplus L_n$. We may decompose
$E = L_1 \oplus \ldots \oplus L_n$. We may decompose ![]() $s, t$ into sections
$s, t$ into sections ![]() $s_i, t_i \in \Gamma(X, L_i)$ for each i. Since s and t agree on the torus, the same is true for si and ti. By the line bundle case
$s_i, t_i \in \Gamma(X, L_i)$ for each i. Since s and t agree on the torus, the same is true for si and ti. By the line bundle case ![]() $s_i = t_i$ for all i, and hence s = t.
$s_i = t_i$ for all i, and hence s = t.
Lemma 7.7. Let X be a scheme over a semiring R and let E be a vector bundle. Let ![]() $s_A: X(A) \rightarrow E(A)$ be a natural transformation such that
$s_A: X(A) \rightarrow E(A)$ be a natural transformation such that ![]() $s_A(x) \in E_x$ for all x, where A are R-algebras. Then there exists a unique element
$s_A(x) \in E_x$ for all x, where A are R-algebras. Then there exists a unique element ![]() $\check{s} \in \Gamma(X, E)$ which induces sA.
$\check{s} \in \Gamma(X, E)$ which induces sA.
Proof. Let ![]() $\pi:E \to X$ be a projection map, where we view E as a geometric vector bundle. Let
$\pi:E \to X$ be a projection map, where we view E as a geometric vector bundle. Let ![]() $s:X \to E$ be a morphism of schemes corresponding to the given natural transformation. Since
$s:X \to E$ be a morphism of schemes corresponding to the given natural transformation. Since ![]() $s_A(x) \in E_x$, we have that
$s_A(x) \in E_x$, we have that ![]() $\pi\circ s = \text{id}_X$, and hence s is a section of π. The claim follows from the fact that the sections of π bijectively correspond to the elements of
$\pi\circ s = \text{id}_X$, and hence s is a section of π. The claim follows from the fact that the sections of π bijectively correspond to the elements of ![]() $\Gamma(X,E)$.
$\Gamma(X,E)$.
We may use the above results to show that the G-action on an equivariant vector bundle is determined by the action on the part of the vector bundle lying over the torus.
Proposition 7.8. Let X be a toric scheme over an idempotent semifield R Let ![]() $G = U_{\{0\}} \subseteq X$ be the torus. Let E be a vector bundle on X. Let
$G = U_{\{0\}} \subseteq X$ be the torus. Let E be a vector bundle on X. Let ![]() $\beta_1, \beta_2: G \times E \rightarrow E$ be actions which make E into an equivariant vector bundle. If β 1 and β 2 induce the same action on
$\beta_1, \beta_2: G \times E \rightarrow E$ be actions which make E into an equivariant vector bundle. If β 1 and β 2 induce the same action on ![]() $E_{U_{\{0\}}}$, then
$E_{U_{\{0\}}}$, then ![]() $\beta_1 = \beta_2$.
$\beta_1 = \beta_2$.
Proof. Suppose first that E is a trivial vector bundle. Fix a global section v of E. We consider the pullback ![]() $\alpha^* E$ along the action
$\alpha^* E$ along the action ![]() $\alpha:G \times X \rightarrow X$.
$\alpha:G \times X \rightarrow X$.
Let A be an R-algebra. Because fibres are constructed via pullback along a point ![]() $(g, x) \in G(A) \times X(A)$, the fibres of
$(g, x) \in G(A) \times X(A)$, the fibres of ![]() $\alpha^* E$ are given by
$\alpha^* E$ are given by
Note that ![]() $(\beta_1)_A(g, v_x), (\beta_2)_A(g, v_x) \in E_{gx}$. Define
$(\beta_1)_A(g, v_x), (\beta_2)_A(g, v_x) \in E_{gx}$. Define
where we use the identification (28). Hence, we have ![]() $(s_i)_A:G(A) \times X(A) \to \alpha^*E(A)$. Apply lemma 7.7 to obtain global sections
$(s_i)_A:G(A) \times X(A) \to \alpha^*E(A)$. Apply lemma 7.7 to obtain global sections ![]() $\check{s_1}, \check{s_2} \in \Gamma(G\times X, \alpha^*E)$. By assumption, when x is a point of the torus, we have
$\check{s_1}, \check{s_2} \in \Gamma(G\times X, \alpha^*E)$. By assumption, when x is a point of the torus, we have
Hence the functors of points of ![]() $\check{s_1}, \check{s_2} $ agree on the torus G × G. By lemma 7.6,
$\check{s_1}, \check{s_2} $ agree on the torus G × G. By lemma 7.6, ![]() $\check{s_1} = \check{s_2}$, and hence they induce the same element of each fibre, i.e.,
$\check{s_1} = \check{s_2}$, and hence they induce the same element of each fibre, i.e., ![]() $(\beta_1)_A(g, v_x) = (\beta_2)_A(g, v_x)$ for all x. In particular, letting v range over a basis
$(\beta_1)_A(g, v_x) = (\beta_2)_A(g, v_x)$ for all x. In particular, letting v range over a basis ![]() $v_1, \ldots, v_n$ of global sections of the trivial bundle E, for any
$v_1, \ldots, v_n$ of global sections of the trivial bundle E, for any ![]() $x \in X(A)$ there is a basis
$x \in X(A)$ there is a basis ![]() $(v_1)_x, \ldots, (v_n)_x\in E_x$ such that
$(v_1)_x, \ldots, (v_n)_x\in E_x$ such that ![]() $(\beta_1)_A(g, (v_i)_x) = (\beta_2)_A(g, (v_i)_x)$. By linearity, this implies
$(\beta_1)_A(g, (v_i)_x) = (\beta_2)_A(g, (v_i)_x)$. By linearity, this implies ![]() $(\beta_1)_A = (\beta_2)_A$, and hence
$(\beta_1)_A = (\beta_2)_A$, and hence ![]() $\beta_1=\beta_2$.
$\beta_1=\beta_2$.
Now consider the general case. For any cone σ, ![]() $E_{U_{\sigma}}$ is trivial by proposition 2.19. The actions on
$E_{U_{\sigma}}$ is trivial by proposition 2.19. The actions on ![]() $E_{U_{\sigma}}$ induced by β 1 and β 2 agree on the torus, so are equal. Since this is true for all σ, the result follows from proposition 7.2.
$E_{U_{\sigma}}$ induced by β 1 and β 2 agree on the torus, so are equal. Since this is true for all σ, the result follows from proposition 7.2.
Another technique for relating equivariant line bundles over toric schemes to line bundles over the torus is the following result.
Lemma 7.9. Let XR be an affine toric scheme over an idempotent semifield R and let ![]() $G_R = U_{\{0\}}$ be the torus. Let L be a line bundle on XR. Then restriction of the action yields a one-to-one correspondence between G-actions on L which make it an equivariant line bundle and G-actions on
$G_R = U_{\{0\}}$ be the torus. Let L be a line bundle on XR. Then restriction of the action yields a one-to-one correspondence between G-actions on L which make it an equivariant line bundle and G-actions on ![]() $L_{U_{\{0\}}}$ which make it an equivariant line bundle.
$L_{U_{\{0\}}}$ which make it an equivariant line bundle.
Proof. By proposition 2.19, L is trivial. By proposition 6.12, it suffices to prove this in the ![]() $\mathbb{F}_1$-case (i.e., monoid schemes). Let G be the torus over
$\mathbb{F}_1$-case (i.e., monoid schemes). Let G be the torus over ![]() $\mathbb{F}_1$ and X be the affine
$\mathbb{F}_1$ and X be the affine ![]() $\mathbb{F}_1$-scheme associated with XR, i.e.,
$\mathbb{F}_1$-scheme associated with XR, i.e., ![]() $X_R = X\otimes_{\mathbb{F}_1}R$. Since G and X are affine, we may apply proposition 6.15 to see that G-actions which make L into an equivariant line bundle are in bijective correspondence with homomorphisms
$X_R = X\otimes_{\mathbb{F}_1}R$. Since G and X are affine, we may apply proposition 6.15 to see that G-actions which make L into an equivariant line bundle are in bijective correspondence with homomorphisms ![]() $\chi: G \rightarrow GL_1$ and this correspondence is such that
$\chi: G \rightarrow GL_1$ and this correspondence is such that
Applying these propositions again, such homomorphisms are in bijective correspondence with G-actions on ![]() $L_{U_{\{0\}}}$ which make it into a line bundle, and this correspondence is such that
$L_{U_{\{0\}}}$ which make it into a line bundle, and this correspondence is such that
Composing the above bijections gives the desired bijective correspondence. It remains to show that the bijection we obtained is given by restricting the equivariant line bundle structure on L to one on ![]() $L_{U_{\{0\}}}$. Let
$L_{U_{\{0\}}}$. Let ![]() $(g, x)\in G(A) \times U_{\{0\}}(A) \subseteq G(A) \times X(A)$. Then in L, g acts on 1x via
$(g, x)\in G(A) \times U_{\{0\}}(A) \subseteq G(A) \times X(A)$. Then in L, g acts on 1x via ![]() $g1_x = \chi(g)1_{gx}$, where
$g1_x = \chi(g)1_{gx}$, where ![]() $\chi: G\rightarrow GL_1$ is the homomorphism corresponding to the action on L. Thus the same is true for the restriction of this action to
$\chi: G\rightarrow GL_1$ is the homomorphism corresponding to the action on L. Thus the same is true for the restriction of this action to ![]() $L_{U_{\{0\}}}$. But the bijection above is given by the property that the action on
$L_{U_{\{0\}}}$. But the bijection above is given by the property that the action on ![]() $L_{U_{\{0\}}}$ satisfies
$L_{U_{\{0\}}}$ satisfies ![]() $g1_x = \chi(g)1_{gx}$, so it agrees with the restriction map.
$g1_x = \chi(g)1_{gx}$, so it agrees with the restriction map.
Proposition 7.10. Let XR be a toric scheme over an idempotent semifield R and let GR be the torus. Let L be a line bundle over XR. Then there is some action that makes L into an equivariant line bundle.
Proof. This is true if L is trivial by example 4.2 and in particular we may make ![]() $L_{U_{\{0\}}}$ into an equivariant line bundle. For each cone σ, we obtain an equivariant vector bundle structure on
$L_{U_{\{0\}}}$ into an equivariant line bundle. For each cone σ, we obtain an equivariant vector bundle structure on ![]() $L_{U_{\sigma}}$ via lemma 7.9. We must check agreement on overlaps. By [Reference Fulton12, Section 1.4], the intersection of two such open sets is given by
$L_{U_{\sigma}}$ via lemma 7.9. We must check agreement on overlaps. By [Reference Fulton12, Section 1.4], the intersection of two such open sets is given by ![]() $U_{\sigma} \cap U_\tau = U_{\sigma \cap \tau}$.
$U_{\sigma} \cap U_\tau = U_{\sigma \cap \tau}$.
We obtain two equivariant line bundle structures on ![]() $L_{U_{\sigma \cap \tau}}$ by restricting the actions on
$L_{U_{\sigma \cap \tau}}$ by restricting the actions on ![]() $L_{U_{\sigma}}$ and
$L_{U_{\sigma}}$ and ![]() $L_{U_\tau}$, respectively. By construction, both agree when restricted further to the torus
$L_{U_\tau}$, respectively. By construction, both agree when restricted further to the torus ![]() $U_{\{0\}}$. Thus we may apply lemma 7.9 to
$U_{\{0\}}$. Thus we may apply lemma 7.9 to ![]() $U_{\sigma \cap \tau}$ to see that both actions on
$U_{\sigma \cap \tau}$ to see that both actions on ![]() $L_{U_{\sigma \cap \tau}}$ are equal. This implies agreement on overlaps, so the result follows from proposition 7.2
$L_{U_{\sigma \cap \tau}}$ are equal. This implies agreement on overlaps, so the result follows from proposition 7.2
We next turn to the problem of classifying equivariant line bundles which are trivial as line bundles. By proposition 6.15, all such equivariant line bundles may be constructed from homomorphisms ![]() $G \rightarrow GL_1$, where G is the torus over
$G \rightarrow GL_1$, where G is the torus over ![]() $\mathbb{F}_1$. The following lemma classifies such homomorphisms.
$\mathbb{F}_1$. The following lemma classifies such homomorphisms.
Lemma 7.11. Let ![]() $\Lambda \subseteq \mathbb{R}^n$ be a lattice (viewed as a group and written multiplicatively). Define the
$\Lambda \subseteq \mathbb{R}^n$ be a lattice (viewed as a group and written multiplicatively). Define the ![]() $\mathbb{F}_1$-scheme G as
$\mathbb{F}_1$-scheme G as ![]() $G = \operatorname{Spec} (\Lambda \cup \{0 \})$. The functor of points of any morphism
$G = \operatorname{Spec} (\Lambda \cup \{0 \})$. The functor of points of any morphism ![]() $\chi: G \rightarrow GL_1$ satisfies
$\chi: G \rightarrow GL_1$ satisfies ![]() $\chi_A(xy) = \chi_A(x) \chi_A(y)$. Moreover, there is an isomorphism between the group of such morphisms and Λ.
$\chi_A(xy) = \chi_A(x) \chi_A(y)$. Moreover, there is an isomorphism between the group of such morphisms and Λ.
Proof. The fact there is an isomorphism between Λ and the group of morphisms ![]() $G\rightarrow GL_1$ follows from lemma 6.1.
$G\rightarrow GL_1$ follows from lemma 6.1.
Let ![]() $\chi:G \rightarrow GL_1$ be a morphism, and let
$\chi:G \rightarrow GL_1$ be a morphism, and let ![]() $u \in \Lambda$ be the corresponding unit. On the level of
$u \in \Lambda$ be the corresponding unit. On the level of ![]() $\mathbb{F}_1$-algebras χ corresponds to the map
$\mathbb{F}_1$-algebras χ corresponds to the map ![]() $\mathbb{Z} \cup \{0\} \rightarrow \Lambda \cup \{0 \}$ sending the generator of
$\mathbb{Z} \cup \{0\} \rightarrow \Lambda \cup \{0 \}$ sending the generator of ![]() $\mathbb{Z}$ to u. Let
$\mathbb{Z}$ to u. Let ![]() $\mu, \pi_1, \pi_2: G \times G \rightarrow G$ be the multiplication and the two projections respectively. The corresponding maps of
$\mu, \pi_1, \pi_2: G \times G \rightarrow G$ be the multiplication and the two projections respectively. The corresponding maps of ![]() $\mathbb{F}_1$-algebras
$\mathbb{F}_1$-algebras ![]() $\Lambda \cup \{0\} \rightarrow (\Lambda \cup \{0\}) \otimes_{\mathbb{F}_1} (\Lambda \cup \{0\})$ are given respectively by
$\Lambda \cup \{0\} \rightarrow (\Lambda \cup \{0\}) \otimes_{\mathbb{F}_1} (\Lambda \cup \{0\})$ are given respectively by ![]() $\mu^*(x) = x \otimes x$,
$\mu^*(x) = x \otimes x$, ![]() $\pi_1^*(x) = x \otimes 1$, and
$\pi_1^*(x) = x \otimes 1$, and ![]() $\pi_2^*(x) = 1 \otimes x$. Hence the same formulas are true for the induced maps on unit groups of
$\pi_2^*(x) = 1 \otimes x$. Hence the same formulas are true for the induced maps on unit groups of ![]() $\mathbb{F}_1$-algebras. Thus we have
$\mathbb{F}_1$-algebras. Thus we have
Reinterpreting this in terms of maps ![]() $G \times G \rightarrow GL_1$ via lemma 6.1, we see that
$G \times G \rightarrow GL_1$ via lemma 6.1, we see that ![]() $\chi \circ \mu$ is given as the product of
$\chi \circ \mu$ is given as the product of ![]() $\chi \circ \pi_1$ and
$\chi \circ \pi_1$ and ![]() $\chi \circ \pi_2$. Rewriting this in terms of functors of points yields
$\chi \circ \pi_2$. Rewriting this in terms of functors of points yields ![]() $\chi_A(xy) = \chi_A(x) \chi_A(y)$.
$\chi_A(xy) = \chi_A(x) \chi_A(y)$.
While each element of Λ yields an action on the trivial line bundle on a toric scheme over ![]() $\mathbb{F}_1$, two such actions might result in isomorphic equivariant line bundles.
$\mathbb{F}_1$, two such actions might result in isomorphic equivariant line bundles.
Lemma 7.12. Let ![]() $X = U_{\sigma}$ be a toric
$X = U_{\sigma}$ be a toric ![]() $\mathbb{F}_1$-scheme corresponding to a cone σ. Let Λ be the dual lattice and G be the corresponding torus. Let
$\mathbb{F}_1$-scheme corresponding to a cone σ. Let Λ be the dual lattice and G be the corresponding torus. Let ![]() $x \in \Lambda$ and let
$x \in \Lambda$ and let ![]() $\chi: G \rightarrow GL_1$ be the corresponding map under lemma 7.11. Then there is some morphism
$\chi: G \rightarrow GL_1$ be the corresponding map under lemma 7.11. Then there is some morphism ![]() $f: X \rightarrow GL_1$ whose functor of points satisfies
$f: X \rightarrow GL_1$ whose functor of points satisfies
if and only if ![]() $x \in (\Lambda \cap \sigma^\vee)^\perp$.
$x \in (\Lambda \cap \sigma^\vee)^\perp$.
Proof. Let ![]() $\alpha:G\times X \to X$ be the action and let
$\alpha:G\times X \to X$ be the action and let ![]() $\pi_i: G \times X \rightarrow X$ be the projections. The condition
$\pi_i: G \times X \rightarrow X$ be the projections. The condition
can be rewritten as follows:
Letting ![]() $x \in \Lambda$ and
$x \in \Lambda$ and  $u \in \Gamma(U_{\sigma}, \mathcal{O}_{U_{\sigma}}^\times) = (\Lambda \cap \sigma^\vee)^\perp$ correspond to χ and f, respectively, under lemma 6.1, the condition (31) may be rewritten as
$u \in \Gamma(U_{\sigma}, \mathcal{O}_{U_{\sigma}}^\times) = (\Lambda \cap \sigma^\vee)^\perp$ correspond to χ and f, respectively, under lemma 6.1, the condition (31) may be rewritten as
The map of ![]() $\mathbb{F}_1$-algebras
$\mathbb{F}_1$-algebras
corresponding to the action ![]() $G \times X \rightarrow X$ is given by
$G \times X \rightarrow X$ is given by ![]() $u \mapsto u \otimes u$, while the projections correspond to algebra homomorphisms given by tensoring with 1. Thus the same is true for the induced maps on unit groups (with tensor replaced by Cartesian product), so the above equation may be rewritten as
$u \mapsto u \otimes u$, while the projections correspond to algebra homomorphisms given by tensoring with 1. Thus the same is true for the induced maps on unit groups (with tensor replaced by Cartesian product), so the above equation may be rewritten as
or simply x = u. So the existence of ![]() $f: X \rightarrow GL_1$ satisfying (30) is equivalent to the existence of
$f: X \rightarrow GL_1$ satisfying (30) is equivalent to the existence of ![]() $u \in (\Lambda \cap \sigma^\vee)^\perp$ satisfying x = u.
$u \in (\Lambda \cap \sigma^\vee)^\perp$ satisfying x = u.
Let X be a toric ![]() $\mathbb{F}_1$-scheme with fan Δ. Let Λ be the dual lattice and G be the corresponding torus. Let
$\mathbb{F}_1$-scheme with fan Δ. Let Λ be the dual lattice and G be the corresponding torus. Let ![]() $x \in \Lambda$ and let
$x \in \Lambda$ and let ![]() $\chi: G \rightarrow GL_1$ be the corresponding map under lemma 7.11. Let
$\chi: G \rightarrow GL_1$ be the corresponding map under lemma 7.11. Let ![]() $\operatorname{Pic}_G(X)$ be the set of isomorphism classes of equivariant line bundles on X. From proposition 4.3,
$\operatorname{Pic}_G(X)$ be the set of isomorphism classes of equivariant line bundles on X. From proposition 4.3, ![]() $\operatorname{Pic}_G(X)$ is a group. Moreover, lemma 7.11 shows that there is a group homomorphism
$\operatorname{Pic}_G(X)$ is a group. Moreover, lemma 7.11 shows that there is a group homomorphism ![]() $\psi:\Lambda \to \operatorname{Pic}_G(X)$. The following proposition characterizes the kernel of ψ.
$\psi:\Lambda \to \operatorname{Pic}_G(X)$. The following proposition characterizes the kernel of ψ.
Proposition 7.13. With the same notation as above, the equivariant line bundle corresponding to χ under proposition 6.15 is isomorphic to the one corresponding to the trivial homomorphism if and only if  $x \in \bigcap\limits_{\sigma \in \Delta} (\Lambda \cap \sigma^\vee)^\perp$.
$x \in \bigcap\limits_{\sigma \in \Delta} (\Lambda \cap \sigma^\vee)^\perp$.
Proof. By lemma 6.17, the equivariant line bundle corresponding to χ is isomorphic to the one corresponding to the trivial character if and only if there is some ![]() $f: X \rightarrow GL_1$ whose functor of points satisfies (30) for all
$f: X \rightarrow GL_1$ whose functor of points satisfies (30) for all ![]() $(g, x)\in G(A) \times X(A)$. By gluing morphisms of schemes, this is equivalent to the existence of a collection of morphisms
$(g, x)\in G(A) \times X(A)$. By gluing morphisms of schemes, this is equivalent to the existence of a collection of morphisms ![]() $f_{\sigma}: U_{\sigma} \rightarrow GL_1$ which satisfy (30) and agree on overlaps.
$f_{\sigma}: U_{\sigma} \rightarrow GL_1$ which satisfy (30) and agree on overlaps.
First we claim that the condition of agreement on overlaps in the above correspondence is true. In fact, since ![]() $U_{\sigma} \cap U_\tau = U_{\sigma \cap \tau}$ is itself toric, in order to check agreement on overlaps, it will suffice by lemma 7.5 and lemma 6.1 to check that all the maps fσ have the same restriction to the torus. Letting 1 be the identity element of the torus, (30) gives
$U_{\sigma} \cap U_\tau = U_{\sigma \cap \tau}$ is itself toric, in order to check agreement on overlaps, it will suffice by lemma 7.5 and lemma 6.1 to check that all the maps fσ have the same restriction to the torus. Letting 1 be the identity element of the torus, (30) gives
The only natural transformation (which is an inclusion) ![]() $i:\operatorname{Spec} \mathbb{F}_1 \rightarrow GL_1$ is the constant map 1 (this follows from lemma 6.1). For any
$i:\operatorname{Spec} \mathbb{F}_1 \rightarrow GL_1$ is the constant map 1 (this follows from lemma 6.1). For any ![]() $\mathbb{F}_1$-algebra A, iA is a map from the one point set
$\mathbb{F}_1$-algebra A, iA is a map from the one point set ![]() $\operatorname{Spec} (\mathbb{F}_1)(A)=\{p\}$ to the group
$\operatorname{Spec} (\mathbb{F}_1)(A)=\{p\}$ to the group ![]() $\text{GL}_1(A)$. One can easily observe that the image of the only point p is the identity element 1 of
$\text{GL}_1(A)$. One can easily observe that the image of the only point p is the identity element 1 of ![]() $\text{GL}_1(A)$. We can write
$\text{GL}_1(A)$. We can write
and ![]() $f_{\sigma} \circ i$ is a morphism from
$f_{\sigma} \circ i$ is a morphism from ![]() $\operatorname{Spec} \mathbb{F}_1$ to
$\operatorname{Spec} \mathbb{F}_1$ to ![]() $\text{GL}_1$. Hence
$\text{GL}_1$. Hence ![]() $(f_{\sigma})_A(1) = 1$ and
$(f_{\sigma})_A(1) = 1$ and ![]() $\chi_A(g) = (f_{\sigma})_A(g)$ for all
$\chi_A(g) = (f_{\sigma})_A(g)$ for all ![]() $g \in G(A) \subseteq U_{\sigma}(A)$, which establishes the claim.
$g \in G(A) \subseteq U_{\sigma}(A)$, which establishes the claim.
It remains to classify χ such that there exists a collection of morphisms ![]() $f_{\sigma}: U_{\sigma} \rightarrow GL_1$ satisfying (30). Since we may construct each fσ independently, it follows from lemma 7.12 that such χ correspond to
$f_{\sigma}: U_{\sigma} \rightarrow GL_1$ satisfying (30). Since we may construct each fσ independently, it follows from lemma 7.12 that such χ correspond to  $x \in \bigcap\limits_{\sigma \in \Delta} (\Lambda \cap \sigma^\vee)^\perp$.
$x \in \bigcap\limits_{\sigma \in \Delta} (\Lambda \cap \sigma^\vee)^\perp$.
Theorem 7.14 7.14 Let R be an idempotent semifield. Let X be a toric scheme over R. Let G be the corresponding torus, Λ be the dual lattice and Δ be the fan corresponding to X. Then there is an exact sequence of abelian groups
 \begin{equation*}
0 \rightarrow \bigcap_{\sigma \in \Delta} (\Lambda \cap \sigma^\vee)^\perp \rightarrow \Lambda \rightarrow \mathrm{Pic}_G(X) \rightarrow \mathrm{Pic}(X) \rightarrow 0 .
\end{equation*}
\begin{equation*}
0 \rightarrow \bigcap_{\sigma \in \Delta} (\Lambda \cap \sigma^\vee)^\perp \rightarrow \Lambda \rightarrow \mathrm{Pic}_G(X) \rightarrow \mathrm{Pic}(X) \rightarrow 0 .
\end{equation*}Proof. Proposition 7.10 tells us that the forgetful morphism ![]() $\phi: \mathrm{Pic}_G(X) \rightarrow \mathrm{Pic}(X)$ is surjective. The combination of proposition 6.15 and lemma 7.11 gives us a group homomorphism
$\phi: \mathrm{Pic}_G(X) \rightarrow \mathrm{Pic}(X)$ is surjective. The combination of proposition 6.15 and lemma 7.11 gives us a group homomorphism ![]() $\psi: \Lambda \rightarrow \mathrm{Pic}_G(X)$ whose image is
$\psi: \Lambda \rightarrow \mathrm{Pic}_G(X)$ whose image is ![]() $\mathrm{ker}(\phi)$. The kernel of ψ is characterized by proposition 7.13.
$\mathrm{ker}(\phi)$. The kernel of ψ is characterized by proposition 7.13.
8. Klyachko theorem for toric schemes over an idempotent semifield
In this section, we prove a version of Klyachko theorem classifying toric vector bundles on a toric scheme over an idempotent semifield K. By a toric line bundle, we mean a torus-equivariant line bundle.
We begin with a gluing construction, which constructs a toric line bundle by gluing together toric line bundles on open subsets corresponding to cones.
Let X be a toric scheme over ![]() $\mathbb{F}_1$ corresponding to a fan Δ with dual lattice Λ. Let S be a set of families
$\mathbb{F}_1$ corresponding to a fan Δ with dual lattice Λ. Let S be a set of families ![]() $u_{\sigma} \in \Lambda$ indexed by cones
$u_{\sigma} \in \Lambda$ indexed by cones ![]() $\sigma\in \Delta$ such that for each such inclusion
$\sigma\in \Delta$ such that for each such inclusion ![]() $\tau\subseteq\sigma$ of cones, the following holds
$\tau\subseteq\sigma$ of cones, the following holds
For cones ![]() $\tau\subseteq\sigma$, we will let
$\tau\subseteq\sigma$, we will let ![]() $\phi_{\sigma\tau} = u_{\sigma}^{-1} u_\tau\in (\Lambda \cap \tau^\vee)^\perp$.
$\phi_{\sigma\tau} = u_{\sigma}^{-1} u_\tau\in (\Lambda \cap \tau^\vee)^\perp$.
Observe that  $(\Lambda \cap \tau^\vee)^\perp = \Gamma(U_{\tau}, \mathcal{O}_{U_\tau}^\times)$, so
$(\Lambda \cap \tau^\vee)^\perp = \Gamma(U_{\tau}, \mathcal{O}_{U_\tau}^\times)$, so ![]() $\phi_{\sigma\tau}$ can be thought of as a morphism
$\phi_{\sigma\tau}$ can be thought of as a morphism ![]() $\phi_{\sigma\tau}: U_\tau \rightarrow \text{GL}_1$ by lemma 6.1. Similarly, we will identify
$\phi_{\sigma\tau}: U_\tau \rightarrow \text{GL}_1$ by lemma 6.1. Similarly, we will identify ![]() $u_{\sigma} \in \Lambda = \Gamma(G, \mathcal{O}_G^\times)$ with a morphism
$u_{\sigma} \in \Lambda = \Gamma(G, \mathcal{O}_G^\times)$ with a morphism ![]() $u_{\sigma}: G\rightarrow \text{GL}_1$, where
$u_{\sigma}: G\rightarrow \text{GL}_1$, where ![]() $G = \operatorname{Spec} (\Lambda \cup \{0\})$ denotes the torus. Lemma 7.11 ensures this morphism is a homomorphism.
$G = \operatorname{Spec} (\Lambda \cup \{0\})$ denotes the torus. Lemma 7.11 ensures this morphism is a homomorphism.
Lemma 8.1. With the same notation as above, for any ![]() $\mathbb{F}_1$-algebra A,
$\mathbb{F}_1$-algebra A, ![]() $g \in G(A)$,
$g \in G(A)$, ![]() $x \in U_\tau(A)$, one has the following
$x \in U_\tau(A)$, one has the following
where we view ![]() $\phi_{\sigma\tau}:U_\tau \to \text{GL}_1$.
$\phi_{\sigma\tau}:U_\tau \to \text{GL}_1$.
Proof. For the notational convenience, we let ![]() $\gamma:=\phi_{\sigma\tau}$. Let
$\gamma:=\phi_{\sigma\tau}$. Let ![]() $T=\left\langle t \right\rangle$ so that
$T=\left\langle t \right\rangle$ so that ![]() $\text{GL}_1=\operatorname{Spec} T$, and
$\text{GL}_1=\operatorname{Spec} T$, and  $M=\Gamma(U_\tau,\mathcal{O}_{U_\tau}^\times)$.
$M=\Gamma(U_\tau,\mathcal{O}_{U_\tau}^\times)$.
In the affine case, lemma 6.1 states that any ![]() $\gamma \in M^\times$ corresponds to the map
$\gamma \in M^\times$ corresponds to the map ![]() $\gamma:T \to M$ sending t to γ. With
$\gamma:T \to M$ sending t to γ. With ![]() $g:\Lambda \to A$ and
$g:\Lambda \to A$ and ![]() $x:M \to A$, we have
$x:M \to A$, we have
where for ![]() $\gamma_A(g)$ we use the fact that
$\gamma_A(g)$ we use the fact that ![]() $M=(\Lambda \cap \tau^\vee)^\perp \subseteq \Lambda$. Since the group structure on
$M=(\Lambda \cap \tau^\vee)^\perp \subseteq \Lambda$. Since the group structure on ![]() $\text{GL}_1$ is given by
$\text{GL}_1$ is given by ![]() $\Delta:T \to T \otimes T$, which sends t to
$\Delta:T \to T \otimes T$, which sends t to ![]() $t\otimes t$, we have
$t\otimes t$, we have
 \begin{align*}
(\gamma_A(g)\gamma_A(x))(t) &= \mu\circ ((g\circ \gamma)\otimes (x\circ \gamma))\circ \Delta(t)=\mu\circ ((g\circ \gamma)(t)\otimes (x\circ \gamma)(t))
\\
&=g(\gamma)x(\gamma),
\end{align*}
\begin{align*}
(\gamma_A(g)\gamma_A(x))(t) &= \mu\circ ((g\circ \gamma)\otimes (x\circ \gamma))\circ \Delta(t)=\mu\circ ((g\circ \gamma)(t)\otimes (x\circ \gamma)(t))
\\
&=g(\gamma)x(\gamma),
\end{align*} where ![]() $\mu:A \otimes A \to A$ is multiplication of A and we identified
$\mu:A \otimes A \to A$ is multiplication of A and we identified ![]() $\gamma(t)$ with the element
$\gamma(t)$ with the element ![]() $\gamma \in M$.
$\gamma \in M$.
Next, let ![]() $\alpha:G \otimes U_\tau \to U_\tau$ be the action of torus. We let
$\alpha:G \otimes U_\tau \to U_\tau$ be the action of torus. We let ![]() $\alpha^*:M \to \Lambda\otimes M$ be the corresponding map sending m to
$\alpha^*:M \to \Lambda\otimes M$ be the corresponding map sending m to ![]() $m\otimes m$. Then, we have
$m\otimes m$. Then, we have
 \begin{align*}
(\gamma_A(gx))(t)=\mu\circ (g\otimes x)\circ \alpha^*\circ \gamma(t) &= \mu\circ (g\otimes x)\circ \alpha^*\circ \gamma(t)\\
&=\mu (g\otimes x)(\gamma \otimes \gamma) = g(\gamma)x(\gamma).
\end{align*}
\begin{align*}
(\gamma_A(gx))(t)=\mu\circ (g\otimes x)\circ \alpha^*\circ \gamma(t) &= \mu\circ (g\otimes x)\circ \alpha^*\circ \gamma(t)\\
&=\mu (g\otimes x)(\gamma \otimes \gamma) = g(\gamma)x(\gamma).
\end{align*}This proves the desired equality (34).
Lemma 8.2. With the same notation as above, there is a surjection from S to the set of isomorphism classes of toric line bundles on X.
The image of ![]() $\{u_{\sigma}\}$ under this map is the unique toric line bundle L which has a family of sections
$\{u_{\sigma}\}$ under this map is the unique toric line bundle L which has a family of sections ![]() $s_{\sigma} \in \Gamma(U_{\sigma}, L)$ such that
$s_{\sigma} \in \Gamma(U_{\sigma}, L)$ such that
and
and such that sσ is a basis over Uσ.
Proof. For each cone σ with our fixed ![]() $u_{\sigma} \in S$, applying proposition 6.15 gives rise to an equivariant line bundle Lσ (whose underlying line bundle is trivial) on Uσ together with a basis sσ of sections for the equivariant line bundle.
$u_{\sigma} \in S$, applying proposition 6.15 gives rise to an equivariant line bundle Lσ (whose underlying line bundle is trivial) on Uσ together with a basis sσ of sections for the equivariant line bundle.
We construct a line bundle L on X by gluing the Lσ together by identifying ![]() $s_{\sigma}\mid_{U_\tau}$ with
$s_{\sigma}\mid_{U_\tau}$ with ![]() $\phi_{\sigma\tau}s_\tau$ for each inclusion of cones
$\phi_{\sigma\tau}s_\tau$ for each inclusion of cones ![]() $\tau\subseteq\sigma$. Lσ is then the restriction of L to Uσ. To be precise, for each
$\tau\subseteq\sigma$. Lσ is then the restriction of L to Uσ. To be precise, for each ![]() $U_{\sigma_i}$ and
$U_{\sigma_i}$ and ![]() $U_{\sigma_j}$ and
$U_{\sigma_j}$ and ![]() $\delta=\sigma_i \cap \sigma_j$, we consider the isomorphism
$\delta=\sigma_i \cap \sigma_j$, we consider the isomorphism
given by
 \begin{equation*}
(s_{\sigma_i})\mid_{U_\delta} \mapsto u_{\sigma_i}^{-1}u_{\sigma_j}(s_{\sigma_j})\mid_{U_\delta}.
\end{equation*}
\begin{equation*}
(s_{\sigma_i})\mid_{U_\delta} \mapsto u_{\sigma_i}^{-1}u_{\sigma_j}(s_{\sigma_j})\mid_{U_\delta}.
\end{equation*} We have to check the cocycle condition ![]() $\psi_{ik}=\psi_{jk}\circ \psi_{ij}$. But, on
$\psi_{ik}=\psi_{jk}\circ \psi_{ij}$. But, on ![]() $U_\tau=U_{\sigma_i} \cap U_{\sigma_j} \cap U_{\sigma_k}$, ψik sends
$U_\tau=U_{\sigma_i} \cap U_{\sigma_j} \cap U_{\sigma_k}$, ψik sends ![]() $(s_{\sigma_i})\mid_{U_\tau}$ to
$(s_{\sigma_i})\mid_{U_\tau}$ to  $u_{\sigma_i}^{-1}u_{\sigma_k}(s_{\sigma_k})\mid_{U_\tau}$, whereas we have
$u_{\sigma_i}^{-1}u_{\sigma_k}(s_{\sigma_k})\mid_{U_\tau}$, whereas we have
 \begin{equation*}
\psi_{jk}(\psi_{ij}((s_{\sigma_i})\mid_{U_\tau}) =\psi_{jk}(u_{\sigma_i}^{-1}u_{\sigma_j}(s_{\sigma_j})\mid_{U_\tau}) =u_{\sigma_i}^{-1}u_{\sigma_j} u_{\sigma_j}^{-1}u_{\sigma_k}(s_{\sigma_k})\mid_{U_\tau},
\end{equation*}
\begin{equation*}
\psi_{jk}(\psi_{ij}((s_{\sigma_i})\mid_{U_\tau}) =\psi_{jk}(u_{\sigma_i}^{-1}u_{\sigma_j}(s_{\sigma_j})\mid_{U_\tau}) =u_{\sigma_i}^{-1}u_{\sigma_j} u_{\sigma_j}^{-1}u_{\sigma_k}(s_{\sigma_k})\mid_{U_\tau},
\end{equation*}showing the cocycle condition.
Now, we show that L is a G-equivariant line bundle. Let A be an ![]() $\mathbb{F}_1$-algebra. We view uσ as a morphism
$\mathbb{F}_1$-algebra. We view uσ as a morphism ![]() $G \to \text{GL}_1$. For the notational convenience, we simply write uσ instead of the following:
$G \to \text{GL}_1$. For the notational convenience, we simply write uσ instead of the following: ![]() $u_{\sigma}(A):G(A) \to \text{GL}_1(A)$. Let
$u_{\sigma}(A):G(A) \to \text{GL}_1(A)$. Let ![]() $g\in G(A)$ and
$g\in G(A)$ and ![]() $x\in U_\tau(A)$. By proposition 6.15, we know that the G-action on Lσ satisfies the following
$x\in U_\tau(A)$. By proposition 6.15, we know that the G-action on Lσ satisfies the following
On the other hand, the G-action on Lτ satisfies
 \begin{align}
g (\phi_{\sigma\tau}(x)(s_\tau)_x)& = \phi_{\sigma\tau}(x) u_\tau(g) (s_{\tau})_{gx} \nonumber\\
&= (\phi_{\sigma\tau}(x) u_\tau(g) \phi_{\sigma\tau}(gx)^{-1})(\phi_{\sigma\tau}(gx)(s_\tau)_{gx}).
\end{align}
\begin{align}
g (\phi_{\sigma\tau}(x)(s_\tau)_x)& = \phi_{\sigma\tau}(x) u_\tau(g) (s_{\tau})_{gx} \nonumber\\
&= (\phi_{\sigma\tau}(x) u_\tau(g) \phi_{\sigma\tau}(gx)^{-1})(\phi_{\sigma\tau}(gx)(s_\tau)_{gx}).
\end{align}We claim
In fact, from lemma 8.1, we have ![]() $\phi_{\sigma\tau}(gx)=\phi_{\sigma\tau}(g)\phi_{\sigma\tau}(x)$. Hence, (37) becomes the following
$\phi_{\sigma\tau}(gx)=\phi_{\sigma\tau}(g)\phi_{\sigma\tau}(x)$. Hence, (37) becomes the following
which is clear from the definition of ![]() $\phi_{\sigma\tau}$.
$\phi_{\sigma\tau}$.
Thus the G-action on Lτ satisfies
 \begin{align}g (s_{\sigma}\mid_{U_\tau})_x& = g (\phi_{\sigma\tau}(x)(s_\tau)_x) = (\phi_{\sigma\tau}(x) u_\tau(g) \phi_{\sigma\tau}(gx)^{-1}) (s_{\sigma}\mid_{U_\tau})_{gx} \nonumber\\
&= u_{\sigma}(g) (s_{\sigma}\mid_{U_\tau})_{gx}
\end{align}
\begin{align}g (s_{\sigma}\mid_{U_\tau})_x& = g (\phi_{\sigma\tau}(x)(s_\tau)_x) = (\phi_{\sigma\tau}(x) u_\tau(g) \phi_{\sigma\tau}(gx)^{-1}) (s_{\sigma}\mid_{U_\tau})_{gx} \nonumber\\
&= u_{\sigma}(g) (s_{\sigma}\mid_{U_\tau})_{gx}
\end{align} and clearly the action on ![]() $(L_{\sigma})_{U_\tau}$ satisfies
$(L_{\sigma})_{U_\tau}$ satisfies ![]() $g (s_{\sigma}\mid_{U_\tau})_x = u_{\sigma}(g) (s_{\sigma}\mid_{U_\tau})_{gx}$ as well. Thus the actions agree.
$g (s_{\sigma}\mid_{U_\tau})_x = u_{\sigma}(g) (s_{\sigma}\mid_{U_\tau})_{gx}$ as well. Thus the actions agree.
By proposition 7.2, the actions on Lσ glue together to make L into an equivariant vector bundle. For surjectivity, we observe that any equivariant vector bundle L can be obtained by gluing together the vector bundles ![]() $L_{U_{\sigma}}$ and the actions on them. The remaining claims are clear from examining the above construction.
$L_{U_{\sigma}}$ and the actions on them. The remaining claims are clear from examining the above construction.
We are now in a position to give a classification of toric line bundles, which does not require knowledge of ![]() $\mathrm{Pic}(X)$.
$\mathrm{Pic}(X)$.
Remark 8.3. One can easily observe that ![]() $(\Lambda \cap \sigma^\vee)^\perp = \Lambda \cap \sigma^\perp$. In particular, proposition 8.4 and corollary 8.7 are precisely the same as toric line bundles on affine toric varieties over a field.
$(\Lambda \cap \sigma^\vee)^\perp = \Lambda \cap \sigma^\perp$. In particular, proposition 8.4 and corollary 8.7 are precisely the same as toric line bundles on affine toric varieties over a field.
Proposition 8.4. Let X be a toric scheme over ![]() $\mathbb{F}_1$ with fan Δ and dual lattice Λ. Then isomorphism classes of toric line bundles on X are in one-to-one correspondence with families of elements
$\mathbb{F}_1$ with fan Δ and dual lattice Λ. Then isomorphism classes of toric line bundles on X are in one-to-one correspondence with families of elements ![]() $[u_{\sigma}]\in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$ indexed by cones, which satisfy the compatibility condition that for
$[u_{\sigma}]\in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$ indexed by cones, which satisfy the compatibility condition that for ![]() $\tau\subseteq\sigma$,
$\tau\subseteq\sigma$, ![]() $[u_\tau]$ is the image of
$[u_\tau]$ is the image of ![]() $[u_{\sigma}]$ under the quotient map
$[u_{\sigma}]$ under the quotient map ![]() $\pi_{\sigma\tau}:\Lambda / (\Lambda \cap \sigma^\vee)^\perp \rightarrow \Lambda / (\Lambda \cap \tau^\vee)^\perp$.
$\pi_{\sigma\tau}:\Lambda / (\Lambda \cap \sigma^\vee)^\perp \rightarrow \Lambda / (\Lambda \cap \tau^\vee)^\perp$.
Proof. Given a family of ![]() $[u_{\sigma}]$ as above, we pick representatives and observe they satisfy the compatibility condition of lemma 8.2. So there is a unique toric line bundle L which locally possesses a basis consisting of a section
$[u_{\sigma}]$ as above, we pick representatives and observe they satisfy the compatibility condition of lemma 8.2. So there is a unique toric line bundle L which locally possesses a basis consisting of a section ![]() $s_{\sigma} \in \Gamma(U_{\sigma}, L)$ with the action given by
$s_{\sigma} \in \Gamma(U_{\sigma}, L)$ with the action given by
under the functor of points and with ![]() $s_{\sigma} = u_{\sigma}^{-1} u_\tau s_\tau$. The desired bijective correspondence f will send
$s_{\sigma} = u_{\sigma}^{-1} u_\tau s_\tau$. The desired bijective correspondence f will send ![]() $\{[u_{\sigma}] \}_{\sigma\in\Delta}\}$ to L.
$\{[u_{\sigma}] \}_{\sigma\in\Delta}\}$ to L.
First we check this is well-defined. Choose representatives uσ of ![]() $[u_{\sigma}]$ and let L and sσ be as above. Let
$[u_{\sigma}]$ and let L and sσ be as above. Let ![]() $v_{\sigma} \in [u_{\sigma_0}]$ be another representative. Then, we have
$v_{\sigma} \in [u_{\sigma_0}]$ be another representative. Then, we have
 \begin{equation*}
u_{\sigma} v_{\sigma}^{-1}\in (\Lambda \cap \sigma^\vee)^\perp = \Gamma(U_{\sigma}, \mathcal{O}_X^\times).
\end{equation*}
\begin{equation*}
u_{\sigma} v_{\sigma}^{-1}\in (\Lambda \cap \sigma^\vee)^\perp = \Gamma(U_{\sigma}, \mathcal{O}_X^\times).
\end{equation*} Thus it makes sense to define sections ![]() $t_{\sigma} = (u_{\sigma} v_{\sigma}^{-1}) s_{\sigma}$. We claim that for each σ, one has the following:
$t_{\sigma} = (u_{\sigma} v_{\sigma}^{-1}) s_{\sigma}$. We claim that for each σ, one has the following:
In fact, with ![]() $\varphi_{\sigma}=u_{\sigma} v_{\sigma}^{-1} $, we have
$\varphi_{\sigma}=u_{\sigma} v_{\sigma}^{-1} $, we have
Hence, we have
 \begin{align*}
g(t_{\sigma})_x &= g (\varphi_{\sigma}(x)(s_{\sigma})_x) = \varphi_{\sigma}(x) u_{\sigma}(g)(s_{\sigma})_{gx} = \varphi_{\sigma}(g^{-1})\varphi_{\sigma}(gx)u_{\sigma}(g)(s_{\sigma})_{gx}\\
&=u_{\sigma}(g^{-1})v_{\sigma}^{-1}(g^{-1})u_{\sigma}(g)\varphi_{\sigma}(gx)(s_{\sigma})_{gx}=v_{\sigma}(g)\varphi_{\sigma}(gx)(s_{\sigma})_{gx}=v_{\sigma}(g)(t_{\sigma})_{gx}.
\end{align*}
\begin{align*}
g(t_{\sigma})_x &= g (\varphi_{\sigma}(x)(s_{\sigma})_x) = \varphi_{\sigma}(x) u_{\sigma}(g)(s_{\sigma})_{gx} = \varphi_{\sigma}(g^{-1})\varphi_{\sigma}(gx)u_{\sigma}(g)(s_{\sigma})_{gx}\\
&=u_{\sigma}(g^{-1})v_{\sigma}^{-1}(g^{-1})u_{\sigma}(g)\varphi_{\sigma}(gx)(s_{\sigma})_{gx}=v_{\sigma}(g)\varphi_{\sigma}(gx)(s_{\sigma})_{gx}=v_{\sigma}(g)(t_{\sigma})_{gx}.
\end{align*}In addition,
Thus L with the sections tσ satisfies the defining property of the line bundle L that is the image of the family of ![]() $[v_{\sigma}]$ under f. Since the families of
$[v_{\sigma}]$ under f. Since the families of ![]() $[u_{\sigma}]$ and
$[u_{\sigma}]$ and ![]() $[v_{\sigma}]$ map the same place under f, f is well-defined.
$[v_{\sigma}]$ map the same place under f, f is well-defined.
Surjectivity follows from the surjectivity in lemma 8.2.
Let ![]() $L, L'$ correspond to
$L, L'$ correspond to ![]() $\{[u_{\sigma}] \}$ and
$\{[u_{\sigma}] \}$ and ![]() $\{[v_{\sigma} ] \}$ respectively. To prove injectivity of f, we suppose
$\{[v_{\sigma} ] \}$ respectively. To prove injectivity of f, we suppose ![]() $L\cong L'$. Then
$L\cong L'$. Then ![]() $L_{U_{\sigma}} \cong L'_{U_{\sigma}}$ for all cones σ. Any line bundle on Uσ is trivial, and
$L_{U_{\sigma}} \cong L'_{U_{\sigma}}$ for all cones σ. Any line bundle on Uσ is trivial, and ![]() $L_{U_{\sigma}}$ has a basis sσ satisfying
$L_{U_{\sigma}}$ has a basis sσ satisfying ![]() $g(s_{\sigma})_x = u_{\sigma}(g) (s_{\sigma})_{gx}$. Thus it corresponds under proposition 6.15 and lemma 7.11 to
$g(s_{\sigma})_x = u_{\sigma}(g) (s_{\sigma})_{gx}$. Thus it corresponds under proposition 6.15 and lemma 7.11 to ![]() $u_{\sigma} \in \Lambda$. The same holds for
$u_{\sigma} \in \Lambda$. The same holds for ![]() $L'_{U_{\sigma}}$ and vσ. By proposition 7.13,
$L'_{U_{\sigma}}$ and vσ. By proposition 7.13, ![]() $u_{\sigma} \cong v_{\sigma}^{-1} \;\mathrm{mod}\, (\Lambda \cap \sigma^\vee)^\perp$. So
$u_{\sigma} \cong v_{\sigma}^{-1} \;\mathrm{mod}\, (\Lambda \cap \sigma^\vee)^\perp$. So ![]() $[u_{\sigma}] = [v_{\sigma}]$, establishing injectivity.
$[u_{\sigma}] = [v_{\sigma}]$, establishing injectivity.
Lemma 8.5. Let Δ be a fan and Λ be the dual lattice. For each cone ![]() $\sigma\in\Delta$, let
$\sigma\in\Delta$, let ![]() $u_{\sigma}\in\Lambda$. The following are equivalent:
$u_{\sigma}\in\Lambda$. The following are equivalent:
(1) For each inclusion of cones
 $\tau\subseteq\sigma$, uσ is congruent to uτ modulo
$\tau\subseteq\sigma$, uσ is congruent to uτ modulo  $(\Lambda \cap \tau^\vee)^\perp$.
$(\Lambda \cap \tau^\vee)^\perp$.(2) For each inclusion of cones
 $\tau\subseteq\sigma$ and each
$\tau\subseteq\sigma$ and each  $x\in \tau$,
$x\in \tau$,  $\langle u_{\sigma}, x\rangle = \langle u_\tau, x\rangle$.
$\langle u_{\sigma}, x\rangle = \langle u_\tau, x\rangle$.(3) For each cone
 $\sigma\in\Delta$ and each ray
$\sigma\in\Delta$ and each ray  $\rho\in\Delta$ with
$\rho\in\Delta$ with  $\rho\subseteq\sigma$,
$\rho\subseteq\sigma$,  $\langle u_{\sigma}, x\rangle = \langle u_\rho, x\rangle$ for all
$\langle u_{\sigma}, x\rangle = \langle u_\rho, x\rangle$ for all  $x \in \rho$.
$x \in \rho$.
Proof. For the proof, we will use the additive notation for Λ.
Suppose uσ is congruent to uτ modulo ![]() $(\Lambda \cap \tau^\vee)^\perp$. Then
$(\Lambda \cap \tau^\vee)^\perp$. Then ![]() $u_{\sigma} - u_\tau\in \tau^\vee$ as is
$u_{\sigma} - u_\tau\in \tau^\vee$ as is ![]() $u_\tau - u_{\sigma}$. So for any
$u_\tau - u_{\sigma}$. So for any ![]() $x\in \tau$, we have both
$x\in \tau$, we have both ![]() $\langle u_{\sigma} - u_\tau, x\rangle \geq 0$ and the reverse inequality. Thus
$\langle u_{\sigma} - u_\tau, x\rangle \geq 0$ and the reverse inequality. Thus ![]() $\langle u_{\sigma}, x\rangle = \langle u_\tau, x\rangle$.
$\langle u_{\sigma}, x\rangle = \langle u_\tau, x\rangle$.
Conversely suppose ![]() $\langle u_{\sigma}, x\rangle = \langle u_\tau, x\rangle$ for all
$\langle u_{\sigma}, x\rangle = \langle u_\tau, x\rangle$ for all ![]() $x\in\tau$. Then
$x\in\tau$. Then ![]() $\langle u_{\sigma} - u_\tau, x\rangle = 0$, so
$\langle u_{\sigma} - u_\tau, x\rangle = 0$, so ![]() $(u_{\sigma} - u_\tau), (u_\tau - u_{\sigma}) \in \tau^\vee$. Since both also belong to Λ,
$(u_{\sigma} - u_\tau), (u_\tau - u_{\sigma}) \in \tau^\vee$. Since both also belong to Λ, ![]() $u_{\sigma} - u_\tau \in (\Lambda \cap \tau^\vee)^\perp$.
$u_{\sigma} - u_\tau \in (\Lambda \cap \tau^\vee)^\perp$.
The second condition trivially implies the third, by taking τ to be a ray and x to be the spanning vector of the ray. Conversely suppose that for each cone σ and each ray ![]() $\rho\subseteq\sigma$, we have
$\rho\subseteq\sigma$, we have ![]() $\langle u_{\sigma}, x\rangle = \langle u_\rho, x\rangle$ for all
$\langle u_{\sigma}, x\rangle = \langle u_\rho, x\rangle$ for all ![]() $x \in \rho$. Let
$x \in \rho$. Let ![]() $\tau\in\Delta$ be such that
$\tau\in\Delta$ be such that ![]() $\tau\subseteq\sigma$. For any ray ρ contained in τ and
$\tau\subseteq\sigma$. For any ray ρ contained in τ and ![]() $x \in \rho$, we have
$x \in \rho$, we have ![]() $\langle u_{\sigma}, x\rangle = \langle u_\rho, x\rangle = \langle u_\tau, x\rangle$. Thus uσ and uτ have the same inner product with any vector in the span of such rays. But each cone in Δ is the span of the rays contained within it, so
$\langle u_{\sigma}, x\rangle = \langle u_\rho, x\rangle = \langle u_\tau, x\rangle$. Thus uσ and uτ have the same inner product with any vector in the span of such rays. But each cone in Δ is the span of the rays contained within it, so ![]() $\langle u_{\sigma}, x\rangle = \langle u_\tau, x\rangle$ for all
$\langle u_{\sigma}, x\rangle = \langle u_\tau, x\rangle$ for all ![]() $x\in\tau$.
$x\in\tau$.
We can recast the classification of line bundles in a form that looks more like Klyachko’s classification.
Corollary 8.6. Let X be a toric scheme over ![]() $\mathbb{F}_1$ with fan Δ and dual lattice Λ. Then isomorphism classes of toric line bundles on X are in one-to-one correspondence with families of elements
$\mathbb{F}_1$ with fan Δ and dual lattice Λ. Then isomorphism classes of toric line bundles on X are in one-to-one correspondence with families of elements ![]() $[u_{\sigma}]\in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$ indexed by cones, which satisfy the compatibility condition that for every ray
$[u_{\sigma}]\in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$ indexed by cones, which satisfy the compatibility condition that for every ray ![]() $\rho\in\Delta$ that is a face of σ,
$\rho\in\Delta$ that is a face of σ, ![]() $\langle u_{\sigma}, x\rangle$ depends only on ρ and not on σ for all
$\langle u_{\sigma}, x\rangle$ depends only on ρ and not on σ for all ![]() $x \in \rho$.
$x \in \rho$.
Corollary 8.7. Let XR be a toric scheme over an idempotent semifield R with fan Δ and dual lattice Λ. Then isomorphism classes of toric line bundles on XR are in one-to-one correspondence with families of elements ![]() $[u_{\sigma}]\in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$ indexed by cones, which satisfy the compatibility condition that for every ray
$[u_{\sigma}]\in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$ indexed by cones, which satisfy the compatibility condition that for every ray ![]() $\rho\in\Delta$ that is a face of σ,
$\rho\in\Delta$ that is a face of σ, ![]() $\langle u_{\sigma}, x \rangle$ depends only on ρ and not on σ for all
$\langle u_{\sigma}, x \rangle$ depends only on ρ and not on σ for all ![]() $x \in \rho$.
$x \in \rho$.
Proof. One may check that lemma 8.2 and proposition 8.4 are still valid with ![]() $X_R=X\otimes R$, where X is the toric scheme over
$X_R=X\otimes R$, where X is the toric scheme over ![]() $\mathbb{F}_1$ associated with Δ.
$\mathbb{F}_1$ associated with Δ.
Definition 8.8. A Klyachko family is a family of elements ![]() $[u_{\sigma}]\in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$ indexed by cones, which satisfy the compatibility condition that for every ray
$[u_{\sigma}]\in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$ indexed by cones, which satisfy the compatibility condition that for every ray ![]() $\rho\in\Delta$ that is a face of σ,
$\rho\in\Delta$ that is a face of σ, ![]() $\langle u_{\sigma}, x \rangle$ for
$\langle u_{\sigma}, x \rangle$ for ![]() $x \in \rho$ depends only on ρ and not on σ.
$x \in \rho$ depends only on ρ and not on σ.
Remark 8.9. A Kylachko family carries the same data as torus-invariant Cartier divisors in toric varieties.
Since equivariant vector bundles decompose uniquely as direct sums of equivariant line bundles, we obtain a classification of equivariant vector bundles.
Corollary 8.10. There is a one-to-one correspondence between isomorphism classes of equivariant vector bundles and Sn-orbits of n-tuples of Klyachko families.
It remains to recast this in a way that looks more like Klyachko’s theorem.
Definition 8.11. A filtration ![]() $E_i\subseteq M$ on a module M over a semiring R indexed by
$E_i\subseteq M$ on a module M over a semiring R indexed by ![]() $\mathbb{Z}$ is called exhaustive if
$\mathbb{Z}$ is called exhaustive if
 \begin{equation*}
\bigcap_{i\in\mathbb{Z}} E_i = 0 \textrm{and } \bigcup_{i\in\mathbb{Z}} E_i = M.
\end{equation*}
\begin{equation*}
\bigcap_{i\in\mathbb{Z}} E_i = 0 \textrm{and } \bigcup_{i\in\mathbb{Z}} E_i = M.
\end{equation*}Definition 8.12. Fix fan Δ and dual lattice Λ. An n-dimensional Δ-Klyachko space over an idempotent semifield K is a free K-module E of rank n with collections of decreasing exhaustive filtrations ![]() $\{E^\rho(n)\}$ indexed by the rays of Δ, satisfying the following compatibility condition: for each cone
$\{E^\rho(n)\}$ indexed by the rays of Δ, satisfying the following compatibility condition: for each cone ![]() $\sigma \in \Delta$, there exists a decomposition
$\sigma \in \Delta$, there exists a decomposition  $E=\bigoplus \limits_{[u] \in \Lambda / (\Lambda \cap \sigma^\vee)^\perp} E_{[u]}$ such that
$E=\bigoplus \limits_{[u] \in \Lambda / (\Lambda \cap \sigma^\vee)^\perp} E_{[u]}$ such that
 \begin{equation*}
E^\rho(i) = \sum_{\left \lt [u],v_\rho\right \gt \geq i}E_{[u]},
\end{equation*}
\begin{equation*}
E^\rho(i) = \sum_{\left \lt [u],v_\rho\right \gt \geq i}E_{[u]},
\end{equation*} for every ![]() $\rho \preceq \sigma$ and
$\rho \preceq \sigma$ and ![]() $i \in \mathbb{Z}$, where vρ is the primitive generator of ρ.
$i \in \mathbb{Z}$, where vρ is the primitive generator of ρ.
Let E and F be Δ-Klyachko spaces over an idempotent semifield K. By a morphism from E to F, we mean a K-linear map ![]() $\phi:E \to F$ such that
$\phi:E \to F$ such that ![]() $\phi(E^\rho(i)) \subseteq F^\rho(i)$ for every ray
$\phi(E^\rho(i)) \subseteq F^\rho(i)$ for every ray ![]() $\rho \in \Delta$ and
$\rho \in \Delta$ and ![]() $i \in \mathbb{Z}$.
$i \in \mathbb{Z}$.
Lemma 8.13. Let E and F be Δ-Klyachko spaces over an idempotent semifield K. Let ![]() $\phi: E \rightarrow F$ be an isomorphism of Δ-Klyachko spaces. Let
$\phi: E \rightarrow F$ be an isomorphism of Δ-Klyachko spaces. Let ![]() $[u]\in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$ for some cone σ. Then
$[u]\in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$ for some cone σ. Then ![]() $\phi(E_{[u]}) = F_{[u]}$.
$\phi(E_{[u]}) = F_{[u]}$.
Proof. Since  $F = \bigoplus\limits_{[v]\in \Lambda / (\Lambda \cap \sigma^\vee)^\perp} F_{[v]}$, and since direct summands of free modules over K are free, there is a basis of F such that every element lies in
$F = \bigoplus\limits_{[v]\in \Lambda / (\Lambda \cap \sigma^\vee)^\perp} F_{[v]}$, and since direct summands of free modules over K are free, there is a basis of F such that every element lies in ![]() $F_{[v]}$ for some v (the basis is a disjoint union of the bases of the summands). Since the basis is unique up to rescaling and permutation, this is in fact true for any basis.
$F_{[v]}$ for some v (the basis is a disjoint union of the bases of the summands). Since the basis is unique up to rescaling and permutation, this is in fact true for any basis.
Fix ![]() $[u]\in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$. Similar to the above observation
$[u]\in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$. Similar to the above observation ![]() $E_{[u]}$ is free with a basis that is a subset of some basis of E. Let
$E_{[u]}$ is free with a basis that is a subset of some basis of E. Let ![]() $e\in E_{[u]}$ be an element of such a basis. Then
$e\in E_{[u]}$ be an element of such a basis. Then ![]() $\phi(e)$ belongs to some basis of F so
$\phi(e)$ belongs to some basis of F so ![]() $\phi(e)\in F_{[v]}$ for some v. It remains to show
$\phi(e)\in F_{[v]}$ for some v. It remains to show ![]() $[v] = [u]$.
$[v] = [u]$.
For any ray ρ that is a face of σ, the minimum i such that ![]() $e \in E^\rho(i)$ is
$e \in E^\rho(i)$ is ![]() $\langle u, v_\rho \rangle$, where vρ is the primitive generator of ρ. Because ϕ is an isomorphism, this must be identical to the minimum i such that
$\langle u, v_\rho \rangle$, where vρ is the primitive generator of ρ. Because ϕ is an isomorphism, this must be identical to the minimum i such that ![]() $\phi(e) \in F^{\rho}(i)$, which is
$\phi(e) \in F^{\rho}(i)$, which is ![]() $\langle v, v_\rho \rangle$. Thus we have
$\langle v, v_\rho \rangle$. Thus we have ![]() $\langle u, v_\rho \rangle = \langle v, v_\rho \rangle$, i.e
$\langle u, v_\rho \rangle = \langle v, v_\rho \rangle$, i.e ![]() $\langle u - v, v_\rho \rangle = 0$. For any
$\langle u - v, v_\rho \rangle = 0$. For any ![]() $w\in \sigma$, w lies in the subspace spanned by such rays, so
$w\in \sigma$, w lies in the subspace spanned by such rays, so ![]() $\langle u - v, w\rangle = 0$. In particular, because u − v and v − u have nonnegative inner product with any
$\langle u - v, w\rangle = 0$. In particular, because u − v and v − u have nonnegative inner product with any ![]() $w\in \sigma$, and since they are elements of Λ,
$w\in \sigma$, and since they are elements of Λ, ![]() $u - v \in (\Lambda \cap \sigma^\vee)^\perp$. So
$u - v \in (\Lambda \cap \sigma^\vee)^\perp$. So ![]() $[u] = [v]$ and hence
$[u] = [v]$ and hence ![]() $\phi(E_{[u]})\subseteq F_{[u]}$. The reverse inclusion follows by applying this result to ϕ −1.
$\phi(E_{[u]})\subseteq F_{[u]}$. The reverse inclusion follows by applying this result to ϕ −1.
Lemma 8.14. There is a one-to-one correspondence between isomorphism classes of n-dimensional Δ-Klyachko spaces over an idempotent semifield K and Sn-orbits of n-tuples of Klyachko families.
Proof. Suppose we are given an n-tuple of Klyachko families, the k-th of which is denoted ![]() $[u_{\sigma, k}] \in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$. For each ray ρ, we let
$[u_{\sigma, k}] \in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$. For each ray ρ, we let
where σ is some cone containing ρ as a face and vρ is the primitive generator of ρ. By the compatibility condition in the definition of Klyachko families, the choice of σ is irrelevant. Now let ![]() $E = K^n$. Let
$E = K^n$. Let ![]() $E^\rho(i)$ be spanned by the standard basis vectors ek such that
$E^\rho(i)$ be spanned by the standard basis vectors ek such that ![]() $i \geq i_{\rho, k}$. One can easily see that this is an exhaustive filtration. For a cone σ, and an element
$i \geq i_{\rho, k}$. One can easily see that this is an exhaustive filtration. For a cone σ, and an element ![]() $[u]\in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$, let
$[u]\in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$, let
Clearly for each k, this latter condition is true for exactly one ![]() $[u]$, so the
$[u]$, so the ![]() $E_{[u]}$ yield a partition of the standard basis and hence
$E_{[u]}$ yield a partition of the standard basis and hence
 \begin{equation}
E=\bigoplus \limits_{[u] \in \Lambda / (\Lambda \cap \sigma^\vee)^\perp} E_{[u]}.
\end{equation}
\begin{equation}
E=\bigoplus \limits_{[u] \in \Lambda / (\Lambda \cap \sigma^\vee)^\perp} E_{[u]}.
\end{equation}For the compatibility condition, recall that
This basis is the disjoint union over ![]() $[u] \in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$ satisfying
$[u] \in \Lambda / (\Lambda \cap \sigma^\vee)^\perp$ satisfying ![]() $i \geq \langle[u],v_\rho\rangle$ of the set of ek such that
$i \geq \langle[u],v_\rho\rangle$ of the set of ek such that ![]() $[u_{\sigma, k}] = [u]$ or equivalently such that ek is an element of the basis of
$[u_{\sigma, k}] = [u]$ or equivalently such that ek is an element of the basis of ![]() $E_{[u]}$. Since the basis of
$E_{[u]}$. Since the basis of ![]() $E^\rho(i)$ is the disjoint union of the bases of such
$E^\rho(i)$ is the disjoint union of the bases of such ![]() $E_{[u]}$,
$E_{[u]}$, ![]() $E^\rho(i)$ is the direct sum of such modules, i.e.,
$E^\rho(i)$ is the direct sum of such modules, i.e.,
 \begin{equation}
E^\rho(i) = \sum_{\left \lt [u],v_\rho\right \gt \geq i}E_{[u]}.
\end{equation}
\begin{equation}
E^\rho(i) = \sum_{\left \lt [u],v_\rho\right \gt \geq i}E_{[u]}.
\end{equation} If we started with a different n-tuple of Klyachko families that belongs to this Sn-orbit, they are related by some permutation ![]() $p \in S_n$, and it is clear that
$p \in S_n$, and it is clear that ![]() $e_k \mapsto e_{p(k)}$ defines an isomorphism between the resulting Δ-Klyachko spaces. So we have a well-defined map from Sn-orbits of n-tuples of Klyachko families to isomorphism classes of Δ-Klyachko spaces.
$e_k \mapsto e_{p(k)}$ defines an isomorphism between the resulting Δ-Klyachko spaces. So we have a well-defined map from Sn-orbits of n-tuples of Klyachko families to isomorphism classes of Δ-Klyachko spaces.
For surjectivity, let E be an n-dimensional Δ-Klyachko space. Write E as a direct sum of 1-dimensional-free modules ![]() $E = L_1 \oplus\ldots\oplus L_n$. Each Li is spanned by a single basis vector of E, and by lemma 2.12, any direct summand of E is spanned by a subset of the basis. So in the direct sum decomposition
$E = L_1 \oplus\ldots\oplus L_n$. Each Li is spanned by a single basis vector of E, and by lemma 2.12, any direct summand of E is spanned by a subset of the basis. So in the direct sum decomposition  $E=\bigoplus \limits_{[u] \in \Lambda / (\Lambda \cap \sigma^\vee)^\perp} E_{[u]}$ corresponding to a cone σ, exactly one
$E=\bigoplus \limits_{[u] \in \Lambda / (\Lambda \cap \sigma^\vee)^\perp} E_{[u]}$ corresponding to a cone σ, exactly one ![]() $E_{[u]}$ contains Lk. Call this
$E_{[u]}$ contains Lk. Call this ![]() $[u_{\sigma, k}]$.
$[u_{\sigma, k}]$.
We claim that ![]() $\{[u_{\sigma,k}]\}_{\sigma \in \Delta,~k=1,\dots,n}$ is an n-tuple of Klyachko family which maps to E under the above construction. In fact, one can easily see that
$\{[u_{\sigma,k}]\}_{\sigma \in \Delta,~k=1,\dots,n}$ is an n-tuple of Klyachko family which maps to E under the above construction. In fact, one can easily see that ![]() $\{[u_{\sigma,k}]\}_{\sigma \in \Delta,~k=1,\dots,n}$ corresponds to E from the above construction, and hence we only have to check that
$\{[u_{\sigma,k}]\}_{\sigma \in \Delta,~k=1,\dots,n}$ corresponds to E from the above construction, and hence we only have to check that ![]() $\langle [u_{\sigma,k}],v_\rho\rangle$ for a ray
$\langle [u_{\sigma,k}],v_\rho\rangle$ for a ray ![]() $\rho \preceq \sigma$ only depends on ρ (not σ). To see this, observe that since
$\rho \preceq \sigma$ only depends on ρ (not σ). To see this, observe that since ![]() $E^\rho(i)$ is a direct sum of isotypical components as in (43), we have the following:
$E^\rho(i)$ is a direct sum of isotypical components as in (43), we have the following:
Since the condition ![]() $L_k \subseteq E^\rho(i)$ does not depend on a choice of σ, the condition
$L_k \subseteq E^\rho(i)$ does not depend on a choice of σ, the condition ![]() $\langle [u_{\sigma,k}],v_\rho\rangle \geq i$ does not depend on a choice of σ either. It follows that the minimum i for which (44) holds, which is
$\langle [u_{\sigma,k}],v_\rho\rangle \geq i$ does not depend on a choice of σ either. It follows that the minimum i for which (44) holds, which is ![]() $\langle [u_{\sigma,k}], v_\rho \rangle$, does not depend on σ. In particular, we have
$\langle [u_{\sigma,k}], v_\rho \rangle$, does not depend on σ. In particular, we have
This shows the compatibility condition, and hence ![]() $\{[u_{\sigma,k}]\}_{\sigma \in \Delta,~k=1,\dots,n}$ is an n-tuple of Klyachko family which maps to E under the above construction.
$\{[u_{\sigma,k}]\}_{\sigma \in \Delta,~k=1,\dots,n}$ is an n-tuple of Klyachko family which maps to E under the above construction.
Now, we prove injectivity. Suppose that we have two n-tuples of Klyachko families ![]() $\{[u_{\sigma}]\}$ and
$\{[u_{\sigma}]\}$ and ![]() $\{[v_{\sigma}]\}$ which give rise to isomorphic Δ-Klyachko spaces E and F. In other words, we have an isomorphism
$\{[v_{\sigma}]\}$ which give rise to isomorphic Δ-Klyachko spaces E and F. In other words, we have an isomorphism ![]() $\varphi:E=K^n \to F=K^n$ of free K-modules such that
$\varphi:E=K^n \to F=K^n$ of free K-modules such that
for every ray ![]() $\rho \in \Delta$ and
$\rho \in \Delta$ and ![]() $i \in \mathbb{Z}$. From proposition 2.13, φ is obtained by permutation of standard basis vectors and their rescaling. Since permuting the standard basis vectors results in another representative in an Sn-orbit of n-tuple of Klyachko families, we may assume that φ is obtained by rescaling the standard basis vectors.
$i \in \mathbb{Z}$. From proposition 2.13, φ is obtained by permutation of standard basis vectors and their rescaling. Since permuting the standard basis vectors results in another representative in an Sn-orbit of n-tuple of Klyachko families, we may assume that φ is obtained by rescaling the standard basis vectors.
Fix a cone ![]() $\sigma \in \Delta$. Let
$\sigma \in \Delta$. Let ![]() $\{[u_{\sigma,k}]\}_{k=1,\dots,n}$ and
$\{[u_{\sigma,k}]\}_{k=1,\dots,n}$ and ![]() $\{[v_{\sigma,k}]\}_{k=1,\dots,n}$ be the elements in the Klyachko families indexed by the cone σ. Now, observe that
$\{[v_{\sigma,k}]\}_{k=1,\dots,n}$ be the elements in the Klyachko families indexed by the cone σ. Now, observe that ![]() $[u_{\sigma,k}]$ is
$[u_{\sigma,k}]$ is ![]() $[u]$ in (41) if
$[u]$ in (41) if ![]() $E_{[u]}$ contains ek, which is true if and only if
$E_{[u]}$ contains ek, which is true if and only if ![]() $F_{[u]}$ contains
$F_{[u]}$ contains ![]() $a_ke_k$ for some
$a_ke_k$ for some ![]() $a_k \in K^*$. This in turn holds if and only if
$a_k \in K^*$. This in turn holds if and only if ![]() $e_k \in F[u]$, which is equivalent to
$e_k \in F[u]$, which is equivalent to ![]() $[u]=[v_{\sigma,k}]$. This proves injectivity.
$[u]=[v_{\sigma,k}]$. This proves injectivity.
We thus have proved the following version of tropical Klyachko theorem from corollary 8.6 and lemma 8.14.
Theorem 8.15 Let K be an idempotent semifield. Let XK be the toric scheme over K associated with a fain Δ. The set of isomorphism classes of toric vector bundles on XK is in one-to-one correspondence with the set of isomorphism classes of Δ-Klyachko spaces over K.
Remark 8.16. A Δ-Klyachko space over ![]() $\mathbb{T}$ naturally determines a tropical toric reflexive sheaf as in [Reference Khan and Maclagan22, Definition 1.1 (Definition 5.1)] as follows: Let
$\mathbb{T}$ naturally determines a tropical toric reflexive sheaf as in [Reference Khan and Maclagan22, Definition 1.1 (Definition 5.1)] as follows: Let ![]() $E=\mathbb{T}^n$ be a Δ-Klyachko space of rank n, for some fan Δ. E gives rise to a simple valuated matroid
$E=\mathbb{T}^n$ be a Δ-Klyachko space of rank n, for some fan Δ. E gives rise to a simple valuated matroid ![]() $\mathcal{M}$ with ground set
$\mathcal{M}$ with ground set ![]() $\{1,2,\dots,n\}$. For each ray
$\{1,2,\dots,n\}$. For each ray ![]() $\rho \in \Delta$, we have the collection
$\rho \in \Delta$, we have the collection ![]() $\{E^\rho(i)\}_{i \in \mathbb{Z}}$. Now, from (42), we can confirm that each
$\{E^\rho(i)\}_{i \in \mathbb{Z}}$. Now, from (42), we can confirm that each ![]() $E^\rho(i)$ is a flat of the underlying matroid
$E^\rho(i)$ is a flat of the underlying matroid ![]() $\underline{\mathcal{M}}$; note that
$\underline{\mathcal{M}}$; note that ![]() $\underline{\mathcal{M}}$ is the free matroid of rank n on
$\underline{\mathcal{M}}$ is the free matroid of rank n on ![]() $\{1,\dots,n\}$. The conditions that
$\{1,\dots,n\}$. The conditions that
(1)
 $E^\rho(j)\leq E^\rho(i)$ if j > i;
$E^\rho(j)\leq E^\rho(i)$ if j > i;(2)
 $E^\rho(i) = \emptyset$ for
$E^\rho(i) = \emptyset$ for  $i \gg 0$;
$i \gg 0$;(3)
 $E^\rho(i) = \{1,\dots,n\}$ for
$E^\rho(i) = \{1,\dots,n\}$ for  $i \ll 0$;
$i \ll 0$;
are clear from the definition (with the order reversed). Now the definition of tropical toric vector bundle [Reference Khan and Maclagan22, Definition 5.4] is a tropical toric reflexive sheaf together with a compatibility condition which is precisely (42).
Acknowledgements
J.J. acknowledges the support of a AMS-Simons Research Enhancement Grant for Primarily Undergraduate Institution (PUI) Faculty during the writing of this paper. K.M. acknowledges the support of Simons Travel Support for Mathematicians. J.J. is grateful to Alex Borisov for helpful discussions. The authors thank Diane Maclagan for her comments and suggestions on the paper.
Appendix A. Toric varieties, toric monoid schemes, and toric schemes over  $\mathbb{T}$
$\mathbb{T}$
We recall how toric varieties, toric monoid schemes and toric schemes over ![]() $\mathbb{T}$ spaces are related and what the ‘torus action’ is in the latter cases. We proceed to define toric vector bundles in each case. This section is largely expository.
$\mathbb{T}$ spaces are related and what the ‘torus action’ is in the latter cases. We proceed to define toric vector bundles in each case. This section is largely expository.
We start with the connection between toric monoid schemes and toric varieties. This correspondence has been observed in [Reference Kato19], [Reference Deitmar11], and [Reference Cortiñas, Haesemeyer, Walker and Weibel8]. The following theorem is well known (For instance, see [Reference Cortiñas, Haesemeyer, Walker and Weibel8, Example 5.8]).
We note that each toric monoid scheme has a unique generic point [Reference Cortiñas, Haesemeyer, Walker and Weibel8, Lemma 2.3 and Theorem 4.4].
Theorem A.1 A.1 Let X be a toric monoid scheme and k a field. Then Xk is a toric variety.
Remark A.2. Theorem A.1 also holds when Xk is reducible. Then the group ![]() $G \cong \mathbb{Z}^r \times F$ for a finite Abelian group F. We denote by
$G \cong \mathbb{Z}^r \times F$ for a finite Abelian group F. We denote by ![]() $\mathcal{G} = \operatorname{Spec} G$ the torus. It is easy to see that
$\mathcal{G} = \operatorname{Spec} G$ the torus. It is easy to see that ![]() $\mathcal{G} = \operatorname{Spec} G$ is dense in X and note that
$\mathcal{G} = \operatorname{Spec} G$ is dense in X and note that ![]() $\mathcal{G}(k) \cong (k^{\times})^{r} \times F$. Since the torus
$\mathcal{G}(k) \cong (k^{\times})^{r} \times F$. Since the torus ![]() $\mathcal{G}_k$ is dense in Xk, it meets every irreducible component of Xk, and F permutes the irreducible components.
$\mathcal{G}_k$ is dense in Xk, it meets every irreducible component of Xk, and F permutes the irreducible components.
In order to understand the torus action ![]() $\mathcal G$ on X, it is enough to do so in the case when X is affine, i.e.,
$\mathcal G$ on X, it is enough to do so in the case when X is affine, i.e., ![]() $X=\operatorname{Spec} A$ for a toric monoid A. Let k be a field and let
$X=\operatorname{Spec} A$ for a toric monoid A. Let k be a field and let ![]() $X_{k} = \operatorname{Spec} k[A]$ and
$X_{k} = \operatorname{Spec} k[A]$ and ![]() $\mathcal{G}_k = \operatorname{Spec} k[G]$. Here Xk is a toric variety with torus
$\mathcal{G}_k = \operatorname{Spec} k[G]$. Here Xk is a toric variety with torus ![]() $\mathcal{G}_k$. By definition, the action of the (dense) torus on itself extends to an action on Xk. The following proposition explains the relation between the points of the toric variety Xk and the monoid scheme X and the actions of the corresponding tori on them.
$\mathcal{G}_k$. By definition, the action of the (dense) torus on itself extends to an action on Xk. The following proposition explains the relation between the points of the toric variety Xk and the monoid scheme X and the actions of the corresponding tori on them.
Proposition A.3. There is an injection from the points of the toric monoid scheme ![]() $X = \operatorname{Spec} A$ to the points of the affine toric variety
$X = \operatorname{Spec} A$ to the points of the affine toric variety ![]() $X_k = \operatorname{Spec} k[A]$. The coaction of the torus on
$X_k = \operatorname{Spec} k[A]$. The coaction of the torus on ![]() $k[A]$ gives rise to a coaction on A, which is constant on the points of X. In particular, there is a one-to-one correspondence between the points of X and the orbits of the torus action.
$k[A]$ gives rise to a coaction on A, which is constant on the points of X. In particular, there is a one-to-one correspondence between the points of X and the orbits of the torus action.
Proof. Consider the map ![]() $\phi: A \rightarrow k[A]$ sending a monomial
$\phi: A \rightarrow k[A]$ sending a monomial ![]() $g \in A$ to
$g \in A$ to ![]() $g \in k[A]$. Let
$g \in k[A]$. Let ![]() $\mathfrak{p} \subset A$ be a prime ideal, then let
$\mathfrak{p} \subset A$ be a prime ideal, then let ![]() $\mathfrak{q}$ be the monomial ideal generated by
$\mathfrak{q}$ be the monomial ideal generated by ![]() $\phi(\mathfrak{p})$. The ideal
$\phi(\mathfrak{p})$. The ideal ![]() $\mathfrak{q}$ is prime. To see this argue by contradiction, assume
$\mathfrak{q}$ is prime. To see this argue by contradiction, assume ![]() $g,h \not\in \mathfrak{q}$ but
$g,h \not\in \mathfrak{q}$ but ![]() $gh \in \mathfrak{q}$. Write g and h as sums of monomials
$gh \in \mathfrak{q}$. Write g and h as sums of monomials  $g = \sum_{i=1}^{k} m_i$ and
$g = \sum_{i=1}^{k} m_i$ and ![]() $h = \sum_{i=1}^{s} n_i$, then
$h = \sum_{i=1}^{s} n_i$, then  $gh = \sum_{i,j} m_i n_j$. Since
$gh = \sum_{i,j} m_i n_j$. Since ![]() $\mathfrak{q}$ is a monomial ideal, if
$\mathfrak{q}$ is a monomial ideal, if ![]() $f \in \mathfrak{q}$ is a polynomial, then each monomial of f are in
$f \in \mathfrak{q}$ is a polynomial, then each monomial of f are in ![]() $\mathfrak{q}$. Thus every monomial
$\mathfrak{q}$. Thus every monomial ![]() $m_i n_j$ of gh is in
$m_i n_j$ of gh is in ![]() $\mathfrak{q}$. Since
$\mathfrak{q}$. Since ![]() $\mathfrak{p}$ is prime, it follows that either mi or nj are in
$\mathfrak{p}$ is prime, it follows that either mi or nj are in ![]() $\mathfrak{p}$ and
$\mathfrak{p}$ and ![]() $\mathfrak{q}$ for every pair
$\mathfrak{q}$ for every pair ![]() $i,j$. Thus we conclude that
$i,j$. Thus we conclude that ![]() $\mathfrak{q}$ is prime.
$\mathfrak{q}$ is prime.
Thus the map ϕ is injective and sends prime ideals in A to monomial prime ideals in ![]() $k[A]$ which are in turn in one-to-one correspondence with orbits of the torus action on the toric variety. The second part follows for the well-known lemma below.
$k[A]$ which are in turn in one-to-one correspondence with orbits of the torus action on the toric variety. The second part follows for the well-known lemma below.
This lemma is a summary of the construction from [Reference Cox, Little and Schenck9, Section 5].
Lemma A.4. Let k be a field, then the ideal ![]() $\mathfrak{a} \subseteq k[A]$ corresponds to a torus invariant irreducible subvariety if and only if
$\mathfrak{a} \subseteq k[A]$ corresponds to a torus invariant irreducible subvariety if and only if ![]() $\mathfrak{a}$ is a monomial ideal.
$\mathfrak{a}$ is a monomial ideal.
Now we look closer at toric schemes as defined in definition 2.5. Toric schemes arise from toric monoid schemes which in turn correspond to fans as shown in [Reference Cortiñas, Haesemeyer, Walker and Weibel8]. In particular, if Δ is a fan, then a toric scheme over a semiring R is covered by open sets isomorphic to ![]() $\operatorname{Spec} R[S_{\sigma}]$, where σ are the cones of Δ and
$\operatorname{Spec} R[S_{\sigma}]$, where σ are the cones of Δ and ![]() $S_{\sigma}:=\sigma^\vee \cap \Lambda$.
$S_{\sigma}:=\sigma^\vee \cap \Lambda$.
Theorem A.5 A.5 Let X be a toric monoid scheme. Via base change to an idempotent semifield K we obtain a toric scheme XK over K with dense torus ![]() $\mathcal{G}_K$ whose action on itself extends to an action on XK.
$\mathcal{G}_K$ whose action on itself extends to an action on XK.
Proof. Let X be toric monoid scheme, and let ![]() $U = \operatorname{Spec} M$ be an affine open subset of X, where M is a cancellative monoid. Each affine open set of X has a unique generic point η. Let G be
$U = \operatorname{Spec} M$ be an affine open subset of X, where M is a cancellative monoid. Each affine open set of X has a unique generic point η. Let G be ![]() $\operatorname{Frac}(M)=\mathcal{O}_{\operatorname{Spec} M, \eta}$. Since G is also the stalk
$\operatorname{Frac}(M)=\mathcal{O}_{\operatorname{Spec} M, \eta}$. Since G is also the stalk ![]() $\mathcal{O}_{X,\eta}$, G does not depend on the choice of U. Since M is cancellative, the quotient map
$\mathcal{O}_{X,\eta}$, G does not depend on the choice of U. Since M is cancellative, the quotient map ![]() $\varphi : M \rightarrow G$ is injective and induces the maps
$\varphi : M \rightarrow G$ is injective and induces the maps ![]() $\varphi_K : K[M] \rightarrow K[G]$ and
$\varphi_K : K[M] \rightarrow K[G]$ and
The last map induces an action of the algebraic group ![]() $\mathcal{G}_K = \operatorname{Spec}\ K[G]$ on
$\mathcal{G}_K = \operatorname{Spec}\ K[G]$ on ![]() $\operatorname{Spec}\ K[M]$ which extends to an action of
$\operatorname{Spec}\ K[M]$ which extends to an action of ![]() $\mathcal{G}_K$ on XK (as this is compatible with the restriction maps of the structure sheaf). To see that that
$\mathcal{G}_K$ on XK (as this is compatible with the restriction maps of the structure sheaf). To see that that ![]() $\mathcal{G}_K$ is dense in UK, and hence it is dense in XK we refer to the next lemma.
$\mathcal{G}_K$ is dense in UK, and hence it is dense in XK we refer to the next lemma.
Lemma A.6. Let K be an idempotent semifield. Let X be a toric monoid scheme with a dense torus ![]() $\mathcal{G}$. Then
$\mathcal{G}$. Then ![]() $\mathcal{G}_K$ is dense in XK.
$\mathcal{G}_K$ is dense in XK.
Proof. We may assume that X is affine. Since X is a toric monoid scheme, X is irreducible. In particular, XK is irreducible (See the proof of proposition 2.20 in [Reference Jun, Mincheva and Tolliver18]). On the other hand, since ![]() $\mathcal{G}$ is dense in X,
$\mathcal{G}$ is dense in X, ![]() $\mathcal{G}$ contains a generic point of X. It follows that
$\mathcal{G}$ contains a generic point of X. It follows that ![]() $\mathcal{G}_K$ contains a generic point of XK, and hence is dense in XK.
$\mathcal{G}_K$ contains a generic point of XK, and hence is dense in XK.
When toric schemes are defined over the tropical semifield ![]() $\mathbb{T}$, the relationship between toric monoid schemes and toric schemes over
$\mathbb{T}$, the relationship between toric monoid schemes and toric schemes over ![]() $\mathbb{T}$ in the affine case is depicted in the following diagrams in a view of tropicalization.
$\mathbb{T}$ in the affine case is depicted in the following diagrams in a view of tropicalization.

The vertical map on the right is the scheme-theoretic tropicalization of [Reference Giansiracusa and Giansiracusa13]. Whether we are working over a field k or the tropical semifield ![]() $\mathbb{T}$, the torus action of
$\mathbb{T}$, the torus action of ![]() $\mathcal{G}_k$ or
$\mathcal{G}_k$ or ![]() $\mathcal{G}_{\mathbb{T}}$ arises from the monoid scheme as explained in [Reference Cortiñas, Haesemeyer, Walker and Weibel8, Construction 4.2 and Example 5.8] and the proof of theorem A.5. Therefore, the action of the torus commutes with tropicalization on affine open sets. But since localization also commutes with tropicalization (we are localizing at a monomial) the affine pictures glue over the fan. In particular, we have the following commutative diagram.
$\mathcal{G}_{\mathbb{T}}$ arises from the monoid scheme as explained in [Reference Cortiñas, Haesemeyer, Walker and Weibel8, Construction 4.2 and Example 5.8] and the proof of theorem A.5. Therefore, the action of the torus commutes with tropicalization on affine open sets. But since localization also commutes with tropicalization (we are localizing at a monomial) the affine pictures glue over the fan. In particular, we have the following commutative diagram.

Appendix B. Sn as a functor
In this section, we prove that Sn can be seen as a group scheme defined over ![]() $\mathbb{N}$.
$\mathbb{N}$.
Let n be a positive integer and Sn be the symmetric group on n letters. We define the following semiring Rn:
 \begin{equation}
R_n=\frac{\mathbb{N}[e_{\sigma}]_{\sigma \in S_n}}{\left\langle \{e_{\sigma} \cdot e_\tau = 0\}_{\sigma \neq \tau},\sum_{\sigma \in S_n} e_{\sigma} =1 \right\rangle}.
\end{equation}
\begin{equation}
R_n=\frac{\mathbb{N}[e_{\sigma}]_{\sigma \in S_n}}{\left\langle \{e_{\sigma} \cdot e_\tau = 0\}_{\sigma \neq \tau},\sum_{\sigma \in S_n} e_{\sigma} =1 \right\rangle}.
\end{equation} In other words, Rn is generated by elements ![]() $\{e_{\sigma}\}_{\sigma \in S_n}$ with relations
$\{e_{\sigma}\}_{\sigma \in S_n}$ with relations ![]() $e_{\sigma} \cdot e_\tau =0$ for
$e_{\sigma} \cdot e_\tau =0$ for ![]() $\sigma \neq \tau$ and
$\sigma \neq \tau$ and  $\sum\limits_{\sigma \in S_n} e_{\sigma} =1$. Note that with the relations given, one has that
$\sum\limits_{\sigma \in S_n} e_{\sigma} =1$. Note that with the relations given, one has that
We define a comultiplication on Rn as follows:
 \begin{equation}
\Delta(e_{\sigma}) = \sum_\tau e_\tau \otimes e_{\tau^{-1}\sigma}.
\end{equation}
\begin{equation}
\Delta(e_{\sigma}) = \sum_\tau e_\tau \otimes e_{\tau^{-1}\sigma}.
\end{equation}The counit is defined as follows:
 \begin{equation}
\varepsilon: R_n \to \mathbb{N}, \quad e_{\sigma} \mapsto \begin{cases}
1 & \text{if } \sigma= \text{id}, \\
0 & \text{otherwise.}
\end{cases}
\end{equation}
\begin{equation}
\varepsilon: R_n \to \mathbb{N}, \quad e_{\sigma} \mapsto \begin{cases}
1 & \text{if } \sigma= \text{id}, \\
0 & \text{otherwise.}
\end{cases}
\end{equation}The antipode is defined as follows:
Lemma A.1. With the same notation as above, for any semiring A, ![]() $R_n(A):=\operatorname{Hom}(R_n,A)$ is equipped with a natural group structure.
$R_n(A):=\operatorname{Hom}(R_n,A)$ is equipped with a natural group structure.
Proof. For ![]() $f, g \in R_n(A)$, the group multiplication is defined as follows:
$f, g \in R_n(A)$, the group multiplication is defined as follows:
where ![]() $\mu:R_n \otimes_{\mathbb{N}} R_n \to R_n$ is the multiplication.
$\mu:R_n \otimes_{\mathbb{N}} R_n \to R_n$ is the multiplication.
The inverse is given as follows:
The unit is given as follows:
Now, we check the group axioms. To show that e is the identity, we only have to check that ![]() $e*f(e_{\sigma})=f*e(e_{\sigma})=f(e_{\sigma})$ as follows:
$e*f(e_{\sigma})=f*e(e_{\sigma})=f(e_{\sigma})$ as follows:
 \begin{equation*}
f*e(e_{\sigma}) = \mu\circ (f\otimes e)\circ\Delta(e_{\sigma})=\mu\circ (f\otimes e)(\sum_\tau e_\tau \otimes e_{\tau^{-1}\sigma})
\end{equation*}
\begin{equation*}
f*e(e_{\sigma}) = \mu\circ (f\otimes e)\circ\Delta(e_{\sigma})=\mu\circ (f\otimes e)(\sum_\tau e_\tau \otimes e_{\tau^{-1}\sigma})
\end{equation*} \begin{equation*}= \sum_\tau f(e_\tau)e(e_{\tau^{-1}\sigma})=f(e_{\sigma})e(1)=f(e_{\sigma}).
\end{equation*}
\begin{equation*}= \sum_\tau f(e_\tau)e(e_{\tau^{-1}\sigma})=f(e_{\sigma})e(1)=f(e_{\sigma}).
\end{equation*}Likewise,
 \begin{equation*}
e*f(e_{\sigma}) = \mu\circ (e\otimes f)\circ \Delta(e_{\sigma})=\sum_\tau e(e_\tau)f(e_{\tau^{-1}\sigma}) = e(1)f(e_{\sigma})=f(e_{\sigma}).
\end{equation*}
\begin{equation*}
e*f(e_{\sigma}) = \mu\circ (e\otimes f)\circ \Delta(e_{\sigma})=\sum_\tau e(e_\tau)f(e_{\tau^{-1}\sigma}) = e(1)f(e_{\sigma})=f(e_{\sigma}).
\end{equation*} For the existence of inverses, we check ![]() $f*f^{-1}=e$ as follows:
$f*f^{-1}=e$ as follows:
 \begin{equation*}
f*f^{-1}(e_{\sigma})=\sum_\tau f(e_\tau)f(S(e_{\tau^{-1}\sigma}))=\sum_\tau f(e_\tau)f(e_{\sigma^{-1}\tau})
\end{equation*}
\begin{equation*}
f*f^{-1}(e_{\sigma})=\sum_\tau f(e_\tau)f(S(e_{\tau^{-1}\sigma}))=\sum_\tau f(e_\tau)f(e_{\sigma^{-1}\tau})
\end{equation*} \begin{equation*}
=\sum_\tau f(e_\tau e_{\sigma^{-1}\tau}) = \begin{cases}
\sum_\tau f(e_\tau)=1 & \text{if } \sigma=\text{id}, \\
0 & \text{otherwise.}
\end{cases}
\end{equation*}
\begin{equation*}
=\sum_\tau f(e_\tau e_{\sigma^{-1}\tau}) = \begin{cases}
\sum_\tau f(e_\tau)=1 & \text{if } \sigma=\text{id}, \\
0 & \text{otherwise.}
\end{cases}
\end{equation*} In particular, ![]() $f*f^{-1}(e_{\sigma})=e(e_{\sigma})$. Similarly,
$f*f^{-1}(e_{\sigma})=e(e_{\sigma})$. Similarly, ![]() $f^{-1}*f=e$.
$f^{-1}*f=e$.
Finally, we check the associativity: let ![]() $f,g,h \in R_n(A)$,
$f,g,h \in R_n(A)$,
 \begin{equation*}
((f*g)*h)(e_{\sigma})=\sum_\tau (f*g)(e_\tau)h(e_{\tau^{-1}\sigma}) = \sum_\tau \sum_{\delta} f(e_\delta)g(e_{\delta^{-1}\tau}) h(e_{\tau^{-1}\sigma}).
\end{equation*}
\begin{equation*}
((f*g)*h)(e_{\sigma})=\sum_\tau (f*g)(e_\tau)h(e_{\tau^{-1}\sigma}) = \sum_\tau \sum_{\delta} f(e_\delta)g(e_{\delta^{-1}\tau}) h(e_{\tau^{-1}\sigma}).
\end{equation*}On the other hand:
 \begin{equation*}
(f*(g*h))(e_{\sigma})=\sum_{\alpha} f(e_\alpha) (g*h)(e_{\alpha^{-1}\sigma}) = \sum_\alpha \sum_\beta f(e_\alpha)g(e_\beta)h(e_{\beta^{-1}\alpha^{-1}\sigma} ),
\end{equation*}
\begin{equation*}
(f*(g*h))(e_{\sigma})=\sum_{\alpha} f(e_\alpha) (g*h)(e_{\alpha^{-1}\sigma}) = \sum_\alpha \sum_\beta f(e_\alpha)g(e_\beta)h(e_{\beta^{-1}\alpha^{-1}\sigma} ),
\end{equation*} and one can easily see that the two expressions are identical with ![]() $\delta = \alpha$ and
$\delta = \alpha$ and ![]() $\tau = \delta \beta$.
$\tau = \delta \beta$.
Define an element fσ in Rn by
 \begin{equation*}
f_{\sigma} := \sum_{\tau \neq \sigma} e_\tau.
\end{equation*}
\begin{equation*}
f_{\sigma} := \sum_{\tau \neq \sigma} e_\tau.
\end{equation*} Observe that for each σ, ![]() $(e_{\sigma}, f_{\sigma})$ is an idempotent pair. For instance, if n = 2, this is equivalent to the notion of idempotent pairs as in definition 2.10, i.e.,
$(e_{\sigma}, f_{\sigma})$ is an idempotent pair. For instance, if n = 2, this is equivalent to the notion of idempotent pairs as in definition 2.10, i.e.,
In fact, one can observe that Rn is just a direct sum of copies of ![]() $\mathbb{N}$, labelled by elements of Sn.
$\mathbb{N}$, labelled by elements of Sn.
Let ![]() $S_n(A)$ be the group of functions from the set of connected components of
$S_n(A)$ be the group of functions from the set of connected components of ![]() $\operatorname{Spec} A$ to Sn. Then, we have the following.
$\operatorname{Spec} A$ to Sn. Then, we have the following.
Lemma A.2. With the same notation as above, ![]() $\operatorname{Hom}(\operatorname{Spec} A, \operatorname{Spec} R_n)=R_n(A)$ is isomorphic to Sn as a group if
$\operatorname{Hom}(\operatorname{Spec} A, \operatorname{Spec} R_n)=R_n(A)$ is isomorphic to Sn as a group if ![]() $\operatorname{Spec} A$ is connected.
$\operatorname{Spec} A$ is connected.
Proof. Let A be a semiring. A map from ![]() $\operatorname{Spec} A$ to
$\operatorname{Spec} A$ to ![]() $\operatorname{Spec} R_n$ is equivalent to a homomorphism
$\operatorname{Spec} R_n$ is equivalent to a homomorphism ![]() $\varphi:R_n \to A$, which is determined by the elements
$\varphi:R_n \to A$, which is determined by the elements ![]() $\varphi(e_{\sigma})$, for
$\varphi(e_{\sigma})$, for ![]() $e_{\sigma} \in R_n$. Since
$e_{\sigma} \in R_n$. Since ![]() $\operatorname{Spec} A$ is connected, it follows from lemma 2.11 that A has only trivial idempotent pairs. In other words, if (e, f) is an idempotent pair of A, then
$\operatorname{Spec} A$ is connected, it follows from lemma 2.11 that A has only trivial idempotent pairs. In other words, if (e, f) is an idempotent pair of A, then ![]() $\{e,f\} = \{0,1\}$.
$\{e,f\} = \{0,1\}$.
We claim that each ![]() $\varphi \in R_n(A)$ determines a unique element
$\varphi \in R_n(A)$ determines a unique element ![]() $\sigma \in S_n$, giving us a bijection between
$\sigma \in S_n$, giving us a bijection between ![]() $R_n(A)$ and Sn. In fact, for each
$R_n(A)$ and Sn. In fact, for each ![]() $\sigma \in S_n$, the pair
$\sigma \in S_n$, the pair ![]() $(\varphi(e_{\sigma}),\varphi(f_{\sigma}))$ should be a trivial idempotent pair, i.e.,
$(\varphi(e_{\sigma}),\varphi(f_{\sigma}))$ should be a trivial idempotent pair, i.e., ![]() $\varphi(e_{\sigma})$ is either 0 or 1 for each
$\varphi(e_{\sigma})$ is either 0 or 1 for each ![]() $\sigma \in S_n$. It is easy to see from the identity
$\sigma \in S_n$. It is easy to see from the identity ![]() $\sum_{\sigma \in S_n} e_{\sigma} =1$ that
$\sum_{\sigma \in S_n} e_{\sigma} =1$ that ![]() $\varphi(e_{\sigma})=1$ for at least one choice of σ, and from the identities
$\varphi(e_{\sigma})=1$ for at least one choice of σ, and from the identities ![]() $e_{\sigma}\cdot e_\tau=0$ that
$e_{\sigma}\cdot e_\tau=0$ that ![]() $\varphi(e_{\sigma})$ cannot be equal to 1 for two choices of σ. So we have obtained an element of Sn, specifically the unique element such that
$\varphi(e_{\sigma})$ cannot be equal to 1 for two choices of σ. So we have obtained an element of Sn, specifically the unique element such that ![]() $\varphi(e_{\sigma})=1$.
$\varphi(e_{\sigma})=1$.
On the other hand, for a given element σ in Sn, note that there is a unique homomorphism ![]() $\varphi:R_n \to A$ with
$\varphi:R_n \to A$ with ![]() $\varphi(e_{\sigma})=1$ and
$\varphi(e_{\sigma})=1$ and ![]() $\varphi(e_\tau)=0$ for all other τ, since this choice of
$\varphi(e_\tau)=0$ for all other τ, since this choice of ![]() $\varphi(e_\tau)$ satisfies the relation defining Rn. This gives us a desired bijection between
$\varphi(e_\tau)$ satisfies the relation defining Rn. This gives us a desired bijection between ![]() $R_n(A)$ and Sn.
$R_n(A)$ and Sn.
Finally, we need to check the comultiplication in (A.2) is right one to give a canonical isomorphism ![]() $R_n(A) \simeq S_n$ as groups with the above bijection. But, it is a straightforward calculation that
$R_n(A) \simeq S_n$ as groups with the above bijection. But, it is a straightforward calculation that
where we abuse notation by identifying elements of Sn with elements of ![]() $R_n(A)$ via the bijection. Also, the unit
$R_n(A)$ via the bijection. Also, the unit ![]() $e \in R_n(A)$, as in (A.7), maps to the unit in Sn via the bijection.
$e \in R_n(A)$, as in (A.7), maps to the unit in Sn via the bijection.
Showing that this representing object has the correct A-valued points for disconnected A should require an extra condition. Even in the ring-theoretic case, one may need some finiteness condition in order to describe a scheme as the disjoint union of connected components. For example, this is not necessarily true for the spectrum of an infinite Boolean algebra, which is totally disconnected, but in general is not discrete.
Suppose ![]() $\operatorname{Spec} A$ has finitely many connected components but is not connected. Then we can find a non-trivial idempotent pair (e, f). Using the idempotence of e, it is easy to see that eA is a semiring (with identity element e), and similarly for fA. Note that any a in A can be written as ea + fa. Furthermore, if
$\operatorname{Spec} A$ has finitely many connected components but is not connected. Then we can find a non-trivial idempotent pair (e, f). Using the idempotence of e, it is easy to see that eA is a semiring (with identity element e), and similarly for fA. Note that any a in A can be written as ea + fa. Furthermore, if ![]() $a = eb + fc$ then multiplying by f gives fa = fc and similarly ea = eb, so the decomposition as a sum of an element of eA and an element of fA is unique, so we get a bijection between eA × fA and A. One can check that this is a homomorphism. So A is a product of nontrivial semirings, and
$a = eb + fc$ then multiplying by f gives fa = fc and similarly ea = eb, so the decomposition as a sum of an element of eA and an element of fA is unique, so we get a bijection between eA × fA and A. One can check that this is a homomorphism. So A is a product of nontrivial semirings, and ![]() $\operatorname{Spec} A$ is the coproduct
$\operatorname{Spec} A$ is the coproduct ![]() $\operatorname{Spec} eA \bigsqcup \operatorname{Spec} fA$. In particular, if Sn denotes the functor represented by Rn, then we have
$\operatorname{Spec} eA \bigsqcup \operatorname{Spec} fA$. In particular, if Sn denotes the functor represented by Rn, then we have
As in the case for rings, the following holds.
Lemma A.3. With the same notation as above, ![]() $\operatorname{Spec} A$ is homeomorphic to
$\operatorname{Spec} A$ is homeomorphic to ![]() $\operatorname{Spec} eA \bigsqcup \operatorname{Spec} fA$.
$\operatorname{Spec} eA \bigsqcup \operatorname{Spec} fA$.
In particular, ![]() $\operatorname{Spec} eA$ and
$\operatorname{Spec} eA$ and ![]() $\operatorname{Spec} fA$ have fewer connected components. Hence, by inductive hypothesis, elements of
$\operatorname{Spec} fA$ have fewer connected components. Hence, by inductive hypothesis, elements of ![]() $S_n(eA)$ correspond to maps from the connected components of eA to the discrete set Sn, and similarly for fA. By the disjoint union property, a map from the connected components of
$S_n(eA)$ correspond to maps from the connected components of eA to the discrete set Sn, and similarly for fA. By the disjoint union property, a map from the connected components of ![]() $\operatorname{Spec} A$ to Sn is the same as a pair of maps from the connected components of
$\operatorname{Spec} A$ to Sn is the same as a pair of maps from the connected components of ![]() $\operatorname{Spec} eA$ and
$\operatorname{Spec} eA$ and ![]() $\operatorname{Spec} fA$ to Sn, and such pairs correspond to elements of
$\operatorname{Spec} fA$ to Sn, and such pairs correspond to elements of ![]() $S_n(eA) \times S_n(fA) = S_n(A)$. Hence we have the following.
$S_n(eA) \times S_n(fA) = S_n(A)$. Hence we have the following.
Proposition A.4. With the same notation as above, ![]() $R_n(A)$ is isomorphic to Sn if
$R_n(A)$ is isomorphic to Sn if ![]() $\operatorname{Spec} A$ has finitely many connected components.
$\operatorname{Spec} A$ has finitely many connected components.
Remark A.5. In proposition 2.13, we prove that there exists an exact sequence as follows, when A is zero-sum free and has only trivial idempotent pairs:
From proposition A.4, if ![]() $\operatorname{Spec} A$ is the coproduct of connected components, one can obtain an exact sequence (A.8) as a product of copies of the exact sequences in the connected case. A scheme-theoretic version of the above exact sequence is in [Reference Borger and Jun6, Theorem 15.4].
$\operatorname{Spec} A$ is the coproduct of connected components, one can obtain an exact sequence (A.8) as a product of copies of the exact sequences in the connected case. A scheme-theoretic version of the above exact sequence is in [Reference Borger and Jun6, Theorem 15.4].