Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cicalese, Marco
Spadaro, Emanuele Nunzio
and
Zeppieri, Caterina Ida
2011.
Asymptotic analysis of a second-order singular perturbation model for phase transitions.
Calculus of Variations and Partial Differential Equations,
Vol. 41,
Issue. 1-2,
p.
127.
You, Honglian
Yuan, Rong
and
Zhang, Ziheng
2013.
Attractor Bifurcation for Extended Fisher-Kolmogorov Equation.
Abstract and Applied Analysis,
Vol. 2013,
Issue. ,
p.
1.
Baía, Margarida
Barroso, Ana Cristina
Chermisi, Milena
and
Matias, José
2013.
Coupled second order singular perturbations for phase transitions.
Nonlinearity,
Vol. 26,
Issue. 5,
p.
1271.
Burger, M.
Esposito, T.
and
Zeppieri, C. I.
2015.
Second-Order Edge-Penalization in the Ambrosio--Tortorelli functional.
Multiscale Modeling & Simulation,
Vol. 13,
Issue. 4,
p.
1354.
Bonheure, Denis
Földes, Juraj
and
Saldaña, Alberto
2016.
Qualitative properties of solutions to mixed-diffusion bistable equations.
Calculus of Variations and Partial Differential Equations,
Vol. 55,
Issue. 3,
Fonseca, Irene
Hayrapetyan, Gurgen
Leoni, Giovanni
and
Zwicknagl, Barbara
2016.
Domain Formation in Membranes Near the Onset of Instability.
Journal of Nonlinear Science,
Vol. 26,
Issue. 5,
p.
1191.
DUAN, NING
2016.
Optimal control problem for the extended Fisher–Kolmogorov equation.
Proceedings - Mathematical Sciences,
Vol. 126,
Issue. 1,
p.
109.
Dal Maso, Gianni
Fonseca, Irene
and
Leoni, Giovanni
2017.
Asymptotic analysis of second order nonlocal Cahn-Hilliard-type functionals.
Transactions of the American Mathematical Society,
Vol. 370,
Issue. 4,
p.
2785.
Bonheure, Denis
and
Hamel, François
2017.
One-dimensional symmetry and Liouville type results for the fourth order Allen-Cahn equation in ℝ N.
Chinese Annals of Mathematics, Series B,
Vol. 38,
Issue. 1,
p.
149.
Dunbar, Oliver R A
and
Elliott, Charles M
2019.
Binary recovery via phase field regularization for first-arrival traveltime tomography.
Inverse Problems,
Vol. 35,
Issue. 9,
p.
095004.
Ignat, Radu
and
Zorgati, Hamdi
2020.
Dimension Reduction and Optimality of the Uniform State in a Phase-Field-Crystal Model Involving a Higher-Order Functional.
Journal of Nonlinear Science,
Vol. 30,
Issue. 1,
p.
261.
Dunbar, Oliver R. A.
Dunlop, Matthew M.
Elliott, Charles M.
Hoang, Viet Ha
and
Stuart, Andrew M.
2020.
Reconciling Bayesian and Perimeter Regularization for Binary Inversion.
SIAM Journal on Scientific Computing,
Vol. 42,
Issue. 4,
p.
A1984.
Smyrnelis, Panayotis
2021.
Double layered solutions to the extended Fisher–Kolmogorov P.D.E..
Nonlinear Differential Equations and Applications NoDEA,
Vol. 28,
Issue. 5,
Pešić, Anastasija
2023.
Variational models for pattern formation in biomembranes—A Γ‐convergence result.
PAMM,
Vol. 23,
Issue. 4,
Ginster, Janusz
Hayrapetyan, Gurgen
Pešić, Anastasija
and
Zwicknagl, Barbara
2024.
A Sharp Interface Limit of a Nonlocal Variational Model for Pattern Formation in Biomembranes.
SIAM Journal on Mathematical Analysis,
Vol. 56,
Issue. 3,
p.
2818.
Coclite, Giuseppe Maria
and
di Ruvo, Lorenzo
2025.
On Classical Solutions for a Swift–Hohenberg Type Equation.
Mediterranean Journal of Mathematics,
Vol. 22,
Issue. 1,

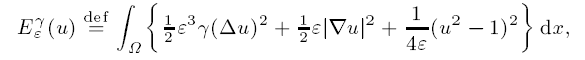
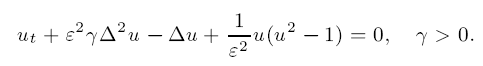
 tends to the area functional in the sense of Γ-limits, where the transition energy is given by the one-dimensional kink of the Extended Fisher–Kolmogorov equation.
tends to the area functional in the sense of Γ-limits, where the transition energy is given by the one-dimensional kink of the Extended Fisher–Kolmogorov equation.