1. Introduction
A recent construction of Dmitry Vaintrob [Reference Vaintrob26, Reference Vaintrob27], shows that the framed little 2-dimensional disks (pseudo)-operad can be modeled as the analytification of a pseudo-operad in log schemes whose underlying schemes are ![]() $\overline{\mathcal M}_{0,n+1}$, the moduli spaces of stable
$\overline{\mathcal M}_{0,n+1}$, the moduli spaces of stable ![]() $(n+1)$-pointed rational curves of genus 0. See also the expositions of Vaintrob’s construction in [Reference Bergström, Diaconu, Petersen and Westerland4] and [Reference Dupont, Panzer and Pym8].
$(n+1)$-pointed rational curves of genus 0. See also the expositions of Vaintrob’s construction in [Reference Bergström, Diaconu, Petersen and Westerland4] and [Reference Dupont, Panzer and Pym8].
This article gives a generalization of Vaintrob’s construction to arbitrary even dimension. For every positive integer d, we construct a pseudo-operad in the category of log varieties whose analytification is weakly equivalent to the 2d-dimensional ![]() $S^1$-framed little disks. We write
$S^1$-framed little disks. We write ![]() $S^1$ for the group
$S^1$ for the group ![]() $U(1)\cong~\text{SO}(2)$ and when we refer to an operad
$U(1)\cong~\text{SO}(2)$ and when we refer to an operad ![]() $\text{\textbf{O}}$ framed by some group G which acts on
$\text{\textbf{O}}$ framed by some group G which acts on ![]() $\textbf{O}$, what is meant is the semidirect operadic product
$\textbf{O}$, what is meant is the semidirect operadic product ![]() $\text{\textbf{O}} \rtimes G$ [Reference Salvatore and Wahl24]. The underlying spaces of the log varieties in
$\text{\textbf{O}} \rtimes G$ [Reference Salvatore and Wahl24]. The underlying spaces of the log varieties in  $\text{\textbf{CGK}}^{\log}_d$ are the moduli spaces for stable n-pointed rooted trees of d-dimensional projective spaces, introduced by Chen, Gibney, and Krashen in [Reference Chen, Gibney and Krashen5] and denoted
$\text{\textbf{CGK}}^{\log}_d$ are the moduli spaces for stable n-pointed rooted trees of d-dimensional projective spaces, introduced by Chen, Gibney, and Krashen in [Reference Chen, Gibney and Krashen5] and denoted ![]() $T_{d,n}$. The connection to Vaintrob’s result is that these moduli spaces are higher dimensional analogs of
$T_{d,n}$. The connection to Vaintrob’s result is that these moduli spaces are higher dimensional analogs of ![]() $\overline{\mathcal M}_{0,n+1}$ and in particular we have that
$\overline{\mathcal M}_{0,n+1}$ and in particular we have that ![]() $T_{1,n} \cong \overline{\mathcal M}_{0,n+1}$. Specifically, we show that the analytification
$T_{1,n} \cong \overline{\mathcal M}_{0,n+1}$. Specifically, we show that the analytification  $\text{\textbf{CGK}}^{\log}_d$ is homeomorphic to
$\text{\textbf{CGK}}^{\log}_d$ is homeomorphic to ![]() $\text{\textbf{FM}}_{2d} \rtimes S^1$, the
$\text{\textbf{FM}}_{2d} \rtimes S^1$, the ![]() $S^1$-framed Fulton–MacPherson operad. By a result of Salvatore [Reference Salvatore23]
$S^1$-framed Fulton–MacPherson operad. By a result of Salvatore [Reference Salvatore23] ![]() $\text{\textbf{FM}}_n$ is
$\text{\textbf{FM}}_n$ is ![]() $\text{SO}(n)$-equivariantly weakly equivalent to
$\text{SO}(n)$-equivariantly weakly equivalent to ![]() $\text{\textbf{LD}}_n$, the classical little disks operad in dimension n. Thus, this homeomorphism gives a weak equivalence between the analytification of
$\text{\textbf{LD}}_n$, the classical little disks operad in dimension n. Thus, this homeomorphism gives a weak equivalence between the analytification of  $\text{\textbf{CGK}}^{\log}_d$ and
$\text{\textbf{CGK}}^{\log}_d$ and ![]() $\text{\textbf{LD}}_{2d}\rtimes S^1$.
$\text{\textbf{LD}}_{2d}\rtimes S^1$.
Theorem 5.12. The Kato–Nakayama analytification of  $\text{\textbf{CGK}}^{\log}_d$ is homeomorphic to
$\text{\textbf{CGK}}^{\log}_d$ is homeomorphic to ![]() $\text{\textbf{FM}}_{2d}\rtimes S^1$.
$\text{\textbf{FM}}_{2d}\rtimes S^1$.
We will also show that the individual spaces ![]() $\text{\textbf{FM}}_{2d}(n)$ are analytifications of log varieties; however, it will not be possible to construct an operad of log schemes with these as objects whose analytification is
$\text{\textbf{FM}}_{2d}(n)$ are analytifications of log varieties; however, it will not be possible to construct an operad of log schemes with these as objects whose analytification is ![]() $\text{\textbf{FM}}_{2d}$. Nevertheless, an operad with this property, which we denote
$\text{\textbf{FM}}_{2d}$. Nevertheless, an operad with this property, which we denote  $\text{\textbf{CGK}}^{\text{V-log}}_d$, can be constructed in the category of log schemes with virtual morphisms. Virtual morphisms of log schemes were introduced by Howell [Reference Howell12] and further studied by Dupont, Panzer, and Pym in a recent article [Reference Dupont, Panzer and Pym8], in which they also show that
$\text{\textbf{CGK}}^{\text{V-log}}_d$, can be constructed in the category of log schemes with virtual morphisms. Virtual morphisms of log schemes were introduced by Howell [Reference Howell12] and further studied by Dupont, Panzer, and Pym in a recent article [Reference Dupont, Panzer and Pym8], in which they also show that ![]() $\text{\textbf{FM}}_2$ is homeomorphic to the analytification of an operad in log schemes with virtual morphisms.
$\text{\textbf{FM}}_2$ is homeomorphic to the analytification of an operad in log schemes with virtual morphisms.
Theorem 5.13. The Kato–Nakayama analytification of  $\text{\textbf{CGK}}^{\text{V-log}}_d$ is homeomorphic to
$\text{\textbf{CGK}}^{\text{V-log}}_d$ is homeomorphic to ![]() $\text{\textbf{FM}}_{2d}$.
$\text{\textbf{FM}}_{2d}$.
This has interesting consequences for the cohomology of ![]() $\text{\textbf{LD}}_{2d}\rtimes S^1$ and
$\text{\textbf{LD}}_{2d}\rtimes S^1$ and ![]() $\text{\textbf{LD}}_{2d}$. First,
$\text{\textbf{LD}}_{2d}$. First,  $\text{\textbf{CGK}}^{\log}_d$ and
$\text{\textbf{CGK}}^{\log}_d$ and  $\text{\textbf{CGK}}^{\text{V-log}}_d$ are defined over
$\text{\textbf{CGK}}^{\text{V-log}}_d$ are defined over ![]() $\mathbb Q$ (and even over
$\mathbb Q$ (and even over ![]() $\mathbb Z$). This induces a Galois action on the corresponding étale cohomology cooperads which lifts to an action on the level of étale cochains. If the weights of cohomology are pure in a suitable sense the existence of such lifts implies formality of the corresponding operad. See for example Petersen [Reference Petersen22]. Additionally, using the log geometric structure of these operads one can define mixed Hodge structures on the respective cohomology cooperads. Such mixed Hodge structures can also be tools for proving operad formality. In fact, Dupont, Panzer, and Pym use the fact that the Hodge structure on the kth cohomology of
$\mathbb Z$). This induces a Galois action on the corresponding étale cohomology cooperads which lifts to an action on the level of étale cochains. If the weights of cohomology are pure in a suitable sense the existence of such lifts implies formality of the corresponding operad. See for example Petersen [Reference Petersen22]. Additionally, using the log geometric structure of these operads one can define mixed Hodge structures on the respective cohomology cooperads. Such mixed Hodge structures can also be tools for proving operad formality. In fact, Dupont, Panzer, and Pym use the fact that the Hodge structure on the kth cohomology of  $\text{\textbf{CGK}}^{\text{V-log}}_1$ is pure of weight 2k to re-prove that
$\text{\textbf{CGK}}^{\text{V-log}}_1$ is pure of weight 2k to re-prove that ![]() $\text{\textbf{LD}}_2$ is formal. It should be noted that all log varieties studied in this article are either smooth varieties with log structure associated to a smooth strict normal crossings divisor or smooth, closed, strong deformation retracts thereof with pulled back log structures. Therefore, it is known how one should define mixed Hodge structures for the log varieties studied in this article but in general the theory of Hodge structures in logarithmic geometry is still under development and there is, to the authors knowledge, no explicit construction of a mixed Hodge structure functor on fs log varieties, even if we restrict to the case of Deligne–Faltings log varieties. Naturally, there is even less material on the matter for log varieties with virtual morphisms. Considering this, it is debatable if the results of this article alone proves that there is a mixed Hodge structure on the cohomologies of
$\text{\textbf{LD}}_2$ is formal. It should be noted that all log varieties studied in this article are either smooth varieties with log structure associated to a smooth strict normal crossings divisor or smooth, closed, strong deformation retracts thereof with pulled back log structures. Therefore, it is known how one should define mixed Hodge structures for the log varieties studied in this article but in general the theory of Hodge structures in logarithmic geometry is still under development and there is, to the authors knowledge, no explicit construction of a mixed Hodge structure functor on fs log varieties, even if we restrict to the case of Deligne–Faltings log varieties. Naturally, there is even less material on the matter for log varieties with virtual morphisms. Considering this, it is debatable if the results of this article alone proves that there is a mixed Hodge structure on the cohomologies of ![]() $\text{\textbf{LD}}_{2d}$ and
$\text{\textbf{LD}}_{2d}$ and ![]() $\text{\textbf{LD}}_{2d} \rtimes S^1$ but hopefully it will be clear to the familiar reader how one can define such a structure using our constructions.
$\text{\textbf{LD}}_{2d} \rtimes S^1$ but hopefully it will be clear to the familiar reader how one can define such a structure using our constructions.
From this one may expect that the construction of this article would imply that either of these formality arguments could be used to prove that the S 1-framed little disks are formal in arbitrary even dimension. However, the argument requires, in some sense, that the weights of cohomology are pure and this is no longer the case for  $\text{\textbf{CGK}}^{\log}_d$ when
$\text{\textbf{CGK}}^{\log}_d$ when ![]() $d\geq 2$. For example, we can create a zig-zag of homotopy equivalences coming from morphisms of log-schemes from
$d\geq 2$. For example, we can create a zig-zag of homotopy equivalences coming from morphisms of log-schemes from  $\text{\textbf{CGK}}^{\log}_d(n)$ to
$\text{\textbf{CGK}}^{\log}_d(n)$ to ![]() $\text{Conf} _n(\mathbb A_{\mathbb{C}}^d)\times \mathbb{G}_m^{n}$ and thus the MHS (mixed Hodge structures) on both these spaces are isomorphic. We know that the MHS on
$\text{Conf} _n(\mathbb A_{\mathbb{C}}^d)\times \mathbb{G}_m^{n}$ and thus the MHS (mixed Hodge structures) on both these spaces are isomorphic. We know that the MHS on ![]() $H^1(\mathbb G_m, \mathbb Q)$ is pure of weight 2 and similarly, the MHS on
$H^1(\mathbb G_m, \mathbb Q)$ is pure of weight 2 and similarly, the MHS on ![]() $H^{2d-1}(\text{Conf} _n(\mathbb A^d_{\mathbb{C}}), \mathbb Q)$ is pure of weight 2d. For d = 2 this implies that the MHS on
$H^{2d-1}(\text{Conf} _n(\mathbb A^d_{\mathbb{C}}), \mathbb Q)$ is pure of weight 2d. For d = 2 this implies that the MHS on ![]() $H^3(\text{Conf} _3(\mathbb A_{\mathbb{C}}^2)\times \mathbb{G}_m^{3},\mathbb Q)\cong \mathbb Q(-2)\oplus \mathbb Q(-3)$ is mixed with weights 4 and 6. In fact, the real model for
$H^3(\text{Conf} _3(\mathbb A_{\mathbb{C}}^2)\times \mathbb{G}_m^{3},\mathbb Q)\cong \mathbb Q(-2)\oplus \mathbb Q(-3)$ is mixed with weights 4 and 6. In fact, the real model for ![]() $\text{\textbf{LD}}_n\rtimes~\text{SO}(n)$ by Khoroshkin and Willwacher in [Reference Khoroshkin and Willwacher14] can be used to construct a real model for
$\text{\textbf{LD}}_n\rtimes~\text{SO}(n)$ by Khoroshkin and Willwacher in [Reference Khoroshkin and Willwacher14] can be used to construct a real model for ![]() $\text{\textbf{LD}}_{2m}\rtimes S^1$ and using this model one can show that
$\text{\textbf{LD}}_{2m}\rtimes S^1$ and using this model one can show that ![]() $\text{\textbf{LD}}_{2m}\rtimes S^1$ is not formal.Footnote 1 On the other hand, the (unframed) little disks are famously known to be formal in every dimension [Reference Kontsevich16, Reference Lambrechts and Volić17].
$\text{\textbf{LD}}_{2m}\rtimes S^1$ is not formal.Footnote 1 On the other hand, the (unframed) little disks are famously known to be formal in every dimension [Reference Kontsevich16, Reference Lambrechts and Volić17].
Even before Vaintrob’s article it had long been expected that the little disks, and the framed little disks are in some sense motivic, or algebro-geometric. A first clue towards this expectation was the Galois action on ![]() $C_*(\text{\textbf{LD}}_2)$ via Grothendieck-Teichmüller theory [Reference Bar-Natan3, Reference Drinfeld7]. This circle of ideas has been developed by a large number of people, including [Reference de Brito, Horel and Kosanović6, Reference Kontsevich16, Reference Morava21, Reference Petersen22].
$C_*(\text{\textbf{LD}}_2)$ via Grothendieck-Teichmüller theory [Reference Bar-Natan3, Reference Drinfeld7]. This circle of ideas has been developed by a large number of people, including [Reference de Brito, Horel and Kosanović6, Reference Kontsevich16, Reference Morava21, Reference Petersen22].
1.1. Structure and results
Section 2 gives a short introduction of logarithmic geometry and in particular we give a definition of Deligne–Faltings, or DF, log schemes and describe their relationship with “normal” log schemes. We also define the real oriented blow-up of a topological space in a section of a vector bundle and we explain how this can be used to give an equivalent definition of the so called Kato–Nakayama analytification [Reference Kato and Nakayama13] of a DF log scheme. Finally, we use the notion of virtual morphisms of log schemes [Reference Dupont, Panzer and Pym8, Reference Howell12] to give a definition of a virtual morphism of DF log schemes and explain why this is interesting.
In section 3 we recall the definition of the topological Fulton–MacPherson compactification and the Fulton–MacPherson model of the little ![]() $D$-dimensional disks operad, denoted
$D$-dimensional disks operad, denoted ![]() $\text{\textbf{FM}}_D$ [Reference Axelrod and Singer2, Reference Getzler and Jones10, Reference Kontsevich15, Reference Sinha25]. We describe an action by
$\text{\textbf{FM}}_D$ [Reference Axelrod and Singer2, Reference Getzler and Jones10, Reference Kontsevich15, Reference Sinha25]. We describe an action by ![]() $\text{SO}(D)$ on
$\text{SO}(D)$ on ![]() $\text{\textbf{FM}}_D$ which is compatible with the corresponding action on
$\text{\textbf{FM}}_D$ which is compatible with the corresponding action on ![]() $\text{\textbf{LD}}_D$, the
$\text{\textbf{LD}}_D$, the ![]() $D$-dimensional little disks operad. In the case where
$D$-dimensional little disks operad. In the case where ![]() $D =2d$ is even this gives an induced action by
$D =2d$ is even this gives an induced action by ![]() $S^1 \cong~\text{SO}(2)$ via the diagonal embedding
$S^1 \cong~\text{SO}(2)$ via the diagonal embedding ![]() $\text{SO}(2) \hookrightarrow~\text{SO}(d)$. This action allows us to define the
$\text{SO}(2) \hookrightarrow~\text{SO}(d)$. This action allows us to define the ![]() $S^1$-framed Fulton–MacPherson operad
$S^1$-framed Fulton–MacPherson operad ![]() $\text{\textbf{FM}}_{2d}\rtimes S^1$ which is weakly equivalent to the
$\text{\textbf{FM}}_{2d}\rtimes S^1$ which is weakly equivalent to the ![]() $S^1$-framed little disks operad.
$S^1$-framed little disks operad.
In section 4 we recall the definition of the schemes ![]() $T_{d,n}$ introduced by Chen, Gibney, and Krashen [Reference Chen, Gibney and Krashen5]. We use a functor of points description of these schemes to define an operad in schemes with objects
$T_{d,n}$ introduced by Chen, Gibney, and Krashen [Reference Chen, Gibney and Krashen5]. We use a functor of points description of these schemes to define an operad in schemes with objects ![]() $T_{d,n}$ for each fixed d. We call this operad the Chen, Gibney, Krashen operad, denoted
$T_{d,n}$ for each fixed d. We call this operad the Chen, Gibney, Krashen operad, denoted ![]() $\text{\textbf{CGK}}_d$.
$\text{\textbf{CGK}}_d$.
Building on this, in section 5 we define Deligne–Faltings log varieties ![]() $\mathsf T_{d,n}$ whose underlying varieties are
$\mathsf T_{d,n}$ whose underlying varieties are ![]() $T_{d,n}$ and we extend the symmetry and composition morphisms (but not the unit morphism) of
$T_{d,n}$ and we extend the symmetry and composition morphisms (but not the unit morphism) of ![]() $\text{\textbf{CGK}}_d$ to maps of these log varieties. This defines a pseudo-operad of log schemes,
$\text{\textbf{CGK}}_d$ to maps of these log varieties. This defines a pseudo-operad of log schemes,  $\text{\textbf{CGK}}^{\log}_d$. We then show that the analytification of
$\text{\textbf{CGK}}^{\log}_d$. We then show that the analytification of  $\text{\textbf{CGK}}^{\log}_d$ is
$\text{\textbf{CGK}}^{\log}_d$ is ![]() $\text{\textbf{FM}}_{2d}\rtimes S^1$. We describe how to define the unit morphism of
$\text{\textbf{FM}}_{2d}\rtimes S^1$. We describe how to define the unit morphism of  $\text{\textbf{CGK}}^{\log}_d$ as a virtual morphism of log schemes and furthermore we show that with virtual morphisms of log schemes we can also define an operad
$\text{\textbf{CGK}}^{\log}_d$ as a virtual morphism of log schemes and furthermore we show that with virtual morphisms of log schemes we can also define an operad  $\text{\textbf{CGK}}^{\text{V-log}}_d$ whose analytification is
$\text{\textbf{CGK}}^{\text{V-log}}_d$ whose analytification is ![]() $\text{\textbf{FM}}_{2d}$.
$\text{\textbf{FM}}_{2d}$.
2. Deligne–Faltings log schemes
We will give all definitions and results relating to logarithmic geometry in this article in terms of Deligne–Faltings log structures. The main reasons for this are that some definitions and results are easier to state using this terminology and, perhaps more importantly, the Kato–Nakayama analytification of a Deligne–Faltings log scheme can be explicitly described in terms of real oriented blow-ups which will turn out to be very useful for the purposes of this article. The precise definition of a DF log scheme may vary between articles but we will use that of Bergström, Diaconu, Petersen, and Westerland [Reference Bergström, Diaconu, Petersen and Westerland4]. In this section we will on some occasions reference “normal” log structures and therefore we will spell out the prefix “DF”. This will not be the case in remaining sections and therefore “log scheme” should be taken to mean “DF log scheme” outside of section 2.
Definition 2.1. A Deligne–Faltings (or DF) log structure on a scheme ![]() $X$ is a finite tuple
$X$ is a finite tuple ![]() $\mathfrak L = (s_i\colon \mathcal O_X \to \mathcal L_i) _{1\leq i \leq n}$ of invertible sheaves with sections. A morphism of log structures on
$\mathfrak L = (s_i\colon \mathcal O_X \to \mathcal L_i) _{1\leq i \leq n}$ of invertible sheaves with sections. A morphism of log structures on ![]() $X$,
$X$,
is a collection ![]() $\{e_{ij}\}$ of non-negative integers together with n isomorphisms of line bundles
$\{e_{ij}\}$ of non-negative integers together with n isomorphisms of line bundles
 \begin{equation*}\mathcal L_i \xrightarrow{\cong} \bigotimes_{1\leq j \leq m}\mathcal M_j^{\otimes e_{ij}}\end{equation*}
\begin{equation*}\mathcal L_i \xrightarrow{\cong} \bigotimes_{1\leq j \leq m}\mathcal M_j^{\otimes e_{ij}}\end{equation*} which also identify the sections si to the corresponding sections  $\bigotimes_{1\leq j \leq m}t_j^{\otimes e_{ij}}$.
$\bigotimes_{1\leq j \leq m}t_j^{\otimes e_{ij}}$.
Remark. For those with a sufficient background in log geometry: A DF log structure ![]() $\mathfrak L = (s_i\colon \mathcal O_X \to \mathcal L_i) _{1\leq i \leq n}$ on some scheme
$\mathfrak L = (s_i\colon \mathcal O_X \to \mathcal L_i) _{1\leq i \leq n}$ on some scheme ![]() $X$ induces a log structure
$X$ induces a log structure ![]() $M(\mathfrak L) = \mathcal M^{\log} \to \mathcal O_X$ where
$M(\mathfrak L) = \mathcal M^{\log} \to \mathcal O_X$ where ![]() $\mathcal M^{\log}$ is the logification of the pre-log structure
$\mathcal M^{\log}$ is the logification of the pre-log structure
 \begin{equation*}\mathcal M(U) = \bigsqcup_{\alpha_i \geq 0} ((\mathcal L_1^\vee)^{\otimes \alpha_1})^* \otimes \dots \otimes \mathcal ((\mathcal L_n^{\vee})^{\otimes \alpha_n})^*\end{equation*}
\begin{equation*}\mathcal M(U) = \bigsqcup_{\alpha_i \geq 0} ((\mathcal L_1^\vee)^{\otimes \alpha_1})^* \otimes \dots \otimes \mathcal ((\mathcal L_n^{\vee})^{\otimes \alpha_n})^*\end{equation*} with the obvious monoid structure and with the map to ![]() $\mathcal O_X$ induced by
$\mathcal O_X$ induced by ![]() $s_i^\vee\colon \mathcal L_i^\vee \to \mathcal O_X$. The superscript
$s_i^\vee\colon \mathcal L_i^\vee \to \mathcal O_X$. The superscript ![]() $*$ here indicates the subsheaf of invertible sections. A morphism of DF log structures induces a map of corresponding log structures in the obvious, functorial, way.
$*$ here indicates the subsheaf of invertible sections. A morphism of DF log structures induces a map of corresponding log structures in the obvious, functorial, way.
Definition 2.2. A DF log scheme ![]() $\mathsf X = (X,\mathfrak L)$ is a scheme
$\mathsf X = (X,\mathfrak L)$ is a scheme ![]() $X$ with a DF log structure
$X$ with a DF log structure ![]() $\mathfrak L$. We call
$\mathfrak L$. We call ![]() $X$ the underlying scheme of
$X$ the underlying scheme of ![]() $\mathsf X$, sometimes denoted
$\mathsf X$, sometimes denoted ![]() $\underline{\mathsf X}$. A morphism of DF log schemes
$\underline{\mathsf X}$. A morphism of DF log schemes ![]() $(X,\mathfrak L) \to (Y,\mathfrak M)$ is a morphism of schemes
$(X,\mathfrak L) \to (Y,\mathfrak M)$ is a morphism of schemes ![]() $f\colon X\to Y$ and a morphism of DF log structures
$f\colon X\to Y$ and a morphism of DF log structures ![]() $f^*\mathfrak M \to \mathfrak L$. Such a morphism is said to be strict if
$f^*\mathfrak M \to \mathfrak L$. Such a morphism is said to be strict if ![]() $f^*\mathfrak M\to \mathfrak L$ is an isomorphism of DF log structures.
$f^*\mathfrak M\to \mathfrak L$ is an isomorphism of DF log structures.
An important special case of a DF log scheme is a scheme with the trivial DF log structure, i.e. no line bundles. For a scheme ![]() $X$ we call
$X$ we call ![]() $(X, \emptyset)$ the log scheme associated to
$(X, \emptyset)$ the log scheme associated to ![]() $X$ and we will, by abuse of notation, simply denote this by
$X$ and we will, by abuse of notation, simply denote this by ![]() $X$. If
$X$. If ![]() $\mathsf Y$ is a log scheme and
$\mathsf Y$ is a log scheme and ![]() $f\colon \underline{\mathsf Y} \to X$ is a map of schemes then there is a unique morphism of log schemes
$f\colon \underline{\mathsf Y} \to X$ is a map of schemes then there is a unique morphism of log schemes ![]() $\mathsf Y \to X$ with underlying map
$\mathsf Y \to X$ with underlying map ![]() $f$. Similarly a morphism
$f$. Similarly a morphism ![]() $f\colon X \to \underline{\mathsf Y}$ gives a morphism of log schemes
$f\colon X \to \underline{\mathsf Y}$ gives a morphism of log schemes ![]() $X \to \mathsf Y$ if and only if the pullbacks via
$X \to \mathsf Y$ if and only if the pullbacks via ![]() $f$ of all line bundles with sections in the log structure of
$f$ of all line bundles with sections in the log structure of ![]() $\mathsf Y$ are trivial with a unit section and if this is the case then this morphism of log schemes is unique.
$\mathsf Y$ are trivial with a unit section and if this is the case then this morphism of log schemes is unique.
2.1. Blow-Ups
In this section we define real oriented blow-ups in sections of line bundles and prove some results relating to these. These will be used to define the Kato–Nakayama analytification of a log scheme.
First, let ![]() $X$ be a topological space, let
$X$ be a topological space, let ![]() $\eta\colon E \to X$ be a rank n vector bundle and let
$\eta\colon E \to X$ be a rank n vector bundle and let ![]() $s\colon X\to E$ be a section. Furthermore, let
$s\colon X\to E$ be a section. Furthermore, let ![]() $E_0$ denote the image of the zero section and let
$E_0$ denote the image of the zero section and let ![]() $E' := E\setminus E_0$. Note that the action by
$E' := E\setminus E_0$. Note that the action by ![]() $\mathbb R_{ \gt 0}$ (and in fact the action by
$\mathbb R_{ \gt 0}$ (and in fact the action by ![]() $\mathbb R^*$) on
$\mathbb R^*$) on ![]() $E$ restricts to a free action on
$E$ restricts to a free action on ![]() $\textstyle E$'. We define the real oriented blow-up of
$\textstyle E$'. We define the real oriented blow-up of ![]() $X$ in s, denoted
$X$ in s, denoted ![]() $\mathrm{Bl}^{\mathbb{R}}_{s}\ X$ as the space
$\mathrm{Bl}^{\mathbb{R}}_{s}\ X$ as the space
and we define the blow-down map ![]() $\rho\colon~\mathrm{Bl}^{\mathbb{R}}_{s}\ X \to X$ as the map induced by passing
$\rho\colon~\mathrm{Bl}^{\mathbb{R}}_{s}\ X \to X$ as the map induced by passing ![]() $p\colon E\to X$ to the quotient. Note that ρ has an inverse away from the zero locus of s and for any x in the zero locus of s we have that
$p\colon E\to X$ to the quotient. Note that ρ has an inverse away from the zero locus of s and for any x in the zero locus of s we have that ![]() $\rho^{-1}(x) \cong S^{n-1}$.
$\rho^{-1}(x) \cong S^{n-1}$.
The “usual” definition of the real oriented blow-up of a smooth manifold ![]() $X$ in a smooth closed sub manifold
$X$ in a smooth closed sub manifold ![]() $Y$, denoted
$Y$, denoted ![]() $\mathrm{Bl}^{\mathbb{R}}_{Y}\ X$ is that it is the complement of a tubular neighbourhood of
$\mathrm{Bl}^{\mathbb{R}}_{Y}\ X$ is that it is the complement of a tubular neighbourhood of ![]() $Y$ in
$Y$ in ![]() $X$ and the blow-down map is then taken to be a retraction of this neighbourhood onto
$X$ and the blow-down map is then taken to be a retraction of this neighbourhood onto ![]() $Y$. It is also possible to give a functorial definition as in [Reference Arone and Kankaanrinta1]. The following result, whose proof I will omit, relates this construction to the usual notion of a blow-up in a smooth closed submanifold.
$Y$. It is also possible to give a functorial definition as in [Reference Arone and Kankaanrinta1]. The following result, whose proof I will omit, relates this construction to the usual notion of a blow-up in a smooth closed submanifold.
Proposition 2.3. Let ![]() $M$ be a (smooth) manifold, let
$M$ be a (smooth) manifold, let ![]() $E$ be a vector bundle, let
$E$ be a vector bundle, let ![]() $s\colon M\to E$ be a smooth section whose image intersects
$s\colon M\to E$ be a smooth section whose image intersects ![]() $E_0$ transversally, and let
$E_0$ transversally, and let ![]() $Y = s^{-1}(E_0)$ be the zero locus of s. Then there is a unique isomorphism of spaces over
$Y = s^{-1}(E_0)$ be the zero locus of s. Then there is a unique isomorphism of spaces over ![]() $M$,
$M$,
Remark. Note that a necessary, but not sufficient, condition here is that the codimension of ![]() $Y$ is the rank of the vector bundle. This resembles the algebraic situation where if
$Y$ is the rank of the vector bundle. This resembles the algebraic situation where if ![]() $X$ is smooth and
$X$ is smooth and ![]() $Y$ is a locally complete intersection the blow-up
$Y$ is a locally complete intersection the blow-up ![]() $\mathrm{Bl}_{Y}\ X$ is locally a closed subscheme of a projective bundle over
$\mathrm{Bl}_{Y}\ X$ is locally a closed subscheme of a projective bundle over ![]() $X$.
$X$.
Despite these properties one should be aware that ![]() $\mathrm{Bl}^{\mathbb{R}}_{s}\ X$ does not always resemble the “usual” definition of a blow-up. For example if we take the blow-up in the zero section of
$\mathrm{Bl}^{\mathbb{R}}_{s}\ X$ does not always resemble the “usual” definition of a blow-up. For example if we take the blow-up in the zero section of ![]() $E$ the result is (up to canonical isomorphism) the sphere bundle of
$E$ the result is (up to canonical isomorphism) the sphere bundle of ![]() $E$ which, in the case where
$E$ which, in the case where ![]() $X$ is a manifold, has higher dimension than
$X$ is a manifold, has higher dimension than ![]() $X$. Even stranger situations are also possible and the blow-up of a manifold is not even necessarily a manifold with corners. For example let
$X$. Even stranger situations are also possible and the blow-up of a manifold is not even necessarily a manifold with corners. For example let ![]() $s\colon S^2\to \mathbb R^2$, considered as a section of a trivial bundle on
$s\colon S^2\to \mathbb R^2$, considered as a section of a trivial bundle on ![]() $S^2$, be defined by
$S^2$, be defined by ![]() $s(x,y,z) = (x-1,0)$. The real oriented blow-up
$s(x,y,z) = (x-1,0)$. The real oriented blow-up ![]() $\mathrm{Bl}^{\mathbb{R}}_{s}\ S^2$ is the wedge sum
$\mathrm{Bl}^{\mathbb{R}}_{s}\ S^2$ is the wedge sum ![]() $S^1\vee S^2$.
$S^1\vee S^2$.
Lemma 2.4. Let ![]() $X$ be a topological space, let
$X$ be a topological space, let ![]() $\pi\colon E\to X$ be a complex line bundle, and let
$\pi\colon E\to X$ be a complex line bundle, and let ![]() $\textstyle E$' be the complement of the zero section in
$\textstyle E$' be the complement of the zero section in ![]() $E$. Then
$E$. Then ![]() $\pi\vert_{E'}^* E \to E'$ is trivial.
$\pi\vert_{E'}^* E \to E'$ is trivial.
Proof. The diagonal map ![]() $E\to E\times_X E$ restricts to a nowhere 0 section,
$E\to E\times_X E$ restricts to a nowhere 0 section, ![]() $E'\to \pi\vert_{E'}^* E$. Thus
$E'\to \pi\vert_{E'}^* E$. Thus ![]() $\pi\vert_{E'}^* E$ is a line bundle with a nowhere 0 section and is hence trivial.
$\pi\vert_{E'}^* E$ is a line bundle with a nowhere 0 section and is hence trivial.
Remark. If ![]() $X$ is a smooth manifold and
$X$ is a smooth manifold and ![]() $E$ is a smooth bundle then
$E$ is a smooth bundle then ![]() $\pi\vert_{E'}^* E \to E'$ is trivial as a smooth bundle by the same argument.
$\pi\vert_{E'}^* E \to E'$ is trivial as a smooth bundle by the same argument.
Corollary 2.5. Let ![]() $s\colon X\to E$ be any section. The pullback of
$s\colon X\to E$ be any section. The pullback of ![]() $E \rightarrow X$ to the blow-up
$E \rightarrow X$ to the blow-up ![]() $\mathrm{Bl}^{\mathbb{R}}_{s}\ X$ is a trivial bundle.
$\mathrm{Bl}^{\mathbb{R}}_{s}\ X$ is a trivial bundle.
Proof. By introducing a Hermitian metric, the blow-up can be embedded into ![]() $E$ʹ and the blow-down map factors via this embedding. Thus, the pullback of
$E$ʹ and the blow-down map factors via this embedding. Thus, the pullback of ![]() $E$ to this blow-up is trivial by lemma 2.4.
$E$ to this blow-up is trivial by lemma 2.4.
Corollary 2.6. Let ![]() $L_1,L_2,\dots, L_n$ be complex line bundles on a manifold
$L_1,L_2,\dots, L_n$ be complex line bundles on a manifold ![]() $X$ and let
$X$ and let  $L=\bigotimes_{i=1}^nL_i^{\otimes e_i}$ where
$L=\bigotimes_{i=1}^nL_i^{\otimes e_i}$ where ![]() $e_i$ are integers and
$e_i$ are integers and ![]() $\otimes$ is the complex tensor product. Let
$\otimes$ is the complex tensor product. Let ![]() $\sigma_1,\dots, \sigma_n$ be sections
$\sigma_1,\dots, \sigma_n$ be sections ![]() $\sigma_i\colon X \to L_i$. Then, there is an isomorphism
$\sigma_i\colon X \to L_i$. Then, there is an isomorphism
 \begin{equation*}\mathrm{Bl}^{\mathbb{R}}_{\tilde \sigma_0}~\mathrm{Bl}^{\mathbb{R}}_{\tilde \sigma_n}\ \dots~\mathrm{Bl}^{\mathbb{R}}_{\sigma_1}\ X \xrightarrow{\cong} \left (\mathrm{Bl}^{\mathbb{R}}_{\tilde \sigma_n}\ \dots~\mathrm{Bl}^{\mathbb{R}}_{\sigma_1}\ X \right )\times S^1\end{equation*}
\begin{equation*}\mathrm{Bl}^{\mathbb{R}}_{\tilde \sigma_0}~\mathrm{Bl}^{\mathbb{R}}_{\tilde \sigma_n}\ \dots~\mathrm{Bl}^{\mathbb{R}}_{\sigma_1}\ X \xrightarrow{\cong} \left (\mathrm{Bl}^{\mathbb{R}}_{\tilde \sigma_n}\ \dots~\mathrm{Bl}^{\mathbb{R}}_{\sigma_1}\ X \right )\times S^1\end{equation*} where ![]() $\tilde \sigma_i$ denotes the pullback of σi through all previous morphisms and
$\tilde \sigma_i$ denotes the pullback of σi through all previous morphisms and ![]() $\sigma_0\colon X\to L$ is the zero section.
$\sigma_0\colon X\to L$ is the zero section.
Proof. This is immediate from the previous corollary.
2.2. Kato–Nakayama analytification
For a DF log scheme ![]() $\mathsf X =(X, (s_i\colon \mathcal O_X \to \mathcal L_i) _{1\leq i \leq n})$ such that
$\mathsf X =(X, (s_i\colon \mathcal O_X \to \mathcal L_i) _{1\leq i \leq n})$ such that ![]() $X$ is of finite type over
$X$ is of finite type over ![]() $\mathbb C$ one can construct an associated topological space
$\mathbb C$ one can construct an associated topological space ![]() $\mathsf X^\text{KN}$ called its Kato–Nakayama analytification. This space is defined as the sequence of real oriented blow-ups
$\mathsf X^\text{KN}$ called its Kato–Nakayama analytification. This space is defined as the sequence of real oriented blow-ups
 \begin{equation*}\mathrm{Bl}^{\mathbb{R}}_{\tilde s_n}~\mathrm{Bl}^{\mathbb{R}}_{\tilde s_{n-1}}\ \dots~\mathrm{Bl}^{\mathbb{R}}_{s_1}\ X^{\text{an}}\end{equation*}
\begin{equation*}\mathrm{Bl}^{\mathbb{R}}_{\tilde s_n}~\mathrm{Bl}^{\mathbb{R}}_{\tilde s_{n-1}}\ \dots~\mathrm{Bl}^{\mathbb{R}}_{s_1}\ X^{\text{an}}\end{equation*} where ![]() $\tilde s_i$ is the section si of the vector bundle
$\tilde s_i$ is the section si of the vector bundle ![]() $\mathcal L_i$ pulled back via all previous blow-ups. This is order independent up to canonical isomorphism since, at each step, we are blowing up in the pullback (i.e. total, not strict, transform) of the corresponding line bundle with section. Regardless of order we let
$\mathcal L_i$ pulled back via all previous blow-ups. This is order independent up to canonical isomorphism since, at each step, we are blowing up in the pullback (i.e. total, not strict, transform) of the corresponding line bundle with section. Regardless of order we let ![]() $\rho_{\mathsf X}\colon \mathsf X^\text{KN} \to X^\text{an}$ denote the corresponding blow-down map. This construction can be made functorial in the following way.
$\rho_{\mathsf X}\colon \mathsf X^\text{KN} \to X^\text{an}$ denote the corresponding blow-down map. This construction can be made functorial in the following way.
First, if ![]() $f\colon (X,(s_i\colon \mathcal O_X \to \mathcal L_i) _{1\leq i \leq n}) \to (Y,(t_i\colon \mathcal O_X \to \mathcal M_i) _{1\leq i \leq n})$ is a strict morphism of log-schemes, i.e a morphism such that the log structure morphism is given by isomorphisms
$f\colon (X,(s_i\colon \mathcal O_X \to \mathcal L_i) _{1\leq i \leq n}) \to (Y,(t_i\colon \mathcal O_X \to \mathcal M_i) _{1\leq i \leq n})$ is a strict morphism of log-schemes, i.e a morphism such that the log structure morphism is given by isomorphisms  $f^*\mathcal M_i \to \mathcal L_i^{\otimes 1}$ for each i, then we can form the following commutative and cartesian (with respect to the downward vertical arrows) diagram
$f^*\mathcal M_i \to \mathcal L_i^{\otimes 1}$ for each i, then we can form the following commutative and cartesian (with respect to the downward vertical arrows) diagram

where we have ![]() $E_X^1 = \mathcal L_1^\text{an}$ and
$E_X^1 = \mathcal L_1^\text{an}$ and ![]() $E_Y^1 = \mathcal M_1^\text{an}$ and where
$E_Y^1 = \mathcal M_1^\text{an}$ and where ![]() $s,t$ are the corresponding sections. The blow-ups
$s,t$ are the corresponding sections. The blow-ups  $\mathrm{Bl}^{\mathbb{R}}_{s_1}\ X(\mathbb C)$ and
$\mathrm{Bl}^{\mathbb{R}}_{s_1}\ X(\mathbb C)$ and  $\mathrm{Bl}^{\mathbb{R}}_{t_1}\ Y(\mathbb C)$ are subspaces of the quotients by an equivalence relation ∼ on
$\mathrm{Bl}^{\mathbb{R}}_{t_1}\ Y(\mathbb C)$ are subspaces of the quotients by an equivalence relation ∼ on ![]() $E_X^1$ and
$E_X^1$ and ![]() $E_Y^1$ respectively where two vectors in a fibre are identified if they are equal up to positive scalar multiplication. By commutativity of the diagram, the subspace corresponding to the blow-up of
$E_Y^1$ respectively where two vectors in a fibre are identified if they are equal up to positive scalar multiplication. By commutativity of the diagram, the subspace corresponding to the blow-up of ![]() $X(\mathbb C)$ is mapped to the blow-up of
$X(\mathbb C)$ is mapped to the blow-up of ![]() $Y(\mathbb C)$ as subspaces of
$Y(\mathbb C)$ as subspaces of ![]() $E_X^1/\sim$ and
$E_X^1/\sim$ and ![]() $E_X^1/\sim$ by the induced quotient space map. Thus, we get an induced subspace map
$E_X^1/\sim$ by the induced quotient space map. Thus, we get an induced subspace map  $\mathrm{Bl}^{\mathbb{R}}_{s_1}\ X(\mathbb C) \to~\mathrm{Bl}^{\mathbb{R}}_{t_1}\ Y(\mathbb C)$. Iterating this gives the desired map of the entire sequence of blow-ups.
$\mathrm{Bl}^{\mathbb{R}}_{s_1}\ X(\mathbb C) \to~\mathrm{Bl}^{\mathbb{R}}_{t_1}\ Y(\mathbb C)$. Iterating this gives the desired map of the entire sequence of blow-ups.
Next, let ![]() $\phi \colon \mathfrak M =(t_j\colon \mathcal O_X \to \mathcal M_j) _{1\leq j \leq m} \to \mathfrak L = (s_i\colon \mathcal O_X \to \mathcal L_i) _{1\leq i \leq n}$ be a morphism of DF log structures on X given by integers
$\phi \colon \mathfrak M =(t_j\colon \mathcal O_X \to \mathcal M_j) _{1\leq j \leq m} \to \mathfrak L = (s_i\colon \mathcal O_X \to \mathcal L_i) _{1\leq i \leq n}$ be a morphism of DF log structures on X given by integers ![]() $\{e_{ij}\}$ and isomorphisms
$\{e_{ij}\}$ and isomorphisms  $\phi_i \colon \mathcal M_i \to \bigotimes_{j}\mathcal L^{\otimes e_{ij}}$. For simplicity assume that all line bundles are trivial. The general case can be constructed from this by gluing. Furthermore, let
$\phi_i \colon \mathcal M_i \to \bigotimes_{j}\mathcal L^{\otimes e_{ij}}$. For simplicity assume that all line bundles are trivial. The general case can be constructed from this by gluing. Furthermore, let ![]() $\pi\colon (X, \mathfrak L)^\text{KN} \to X(\mathbb C)$ and
$\pi\colon (X, \mathfrak L)^\text{KN} \to X(\mathbb C)$ and ![]() $\rho \colon (X,\mathfrak M)^\text{KN} \to X(\mathbb C)$ denote the corresponding blow-down maps. Then, by composing with the trivializing isomorphisms, we obtain a unique invertible algebraic function
$\rho \colon (X,\mathfrak M)^\text{KN} \to X(\mathbb C)$ denote the corresponding blow-down maps. Then, by composing with the trivializing isomorphisms, we obtain a unique invertible algebraic function ![]() $\lambda_i\colon X \to \mathbb C$ such that we can identify the analytification of
$\lambda_i\colon X \to \mathbb C$ such that we can identify the analytification of ![]() $\phi_i$ with a map
$\phi_i$ with a map  $\tilde{\phi_i}\colon X(\mathbb C)\times\mathbb C \to X(\mathbb C)\times\bigotimes_{1\leq j\leq n} \mathbb C^{\otimes e_{ij}}$ which sends
$\tilde{\phi_i}\colon X(\mathbb C)\times\mathbb C \to X(\mathbb C)\times\bigotimes_{1\leq j\leq n} \mathbb C^{\otimes e_{ij}}$ which sends
 \begin{equation*}(x,z) \mapsto (x, \lambda_i(x) z\bigotimes_{1\leq j\leq n} 1^{\otimes e_{ij}}).\end{equation*}
\begin{equation*}(x,z) \mapsto (x, \lambda_i(x) z\bigotimes_{1\leq j\leq n} 1^{\otimes e_{ij}}).\end{equation*} This gives a map of spaces over ![]() $X(\mathbb C)$,
$X(\mathbb C)$, ![]() $X(\mathbb C)\times (\mathbb C^*)^n \to X(\mathbb C)\times (\mathbb C^*)^m$ given by
$X(\mathbb C)\times (\mathbb C^*)^n \to X(\mathbb C)\times (\mathbb C^*)^m$ given by
 \begin{equation*}(x,(z_1,\dots, z_n)) \mapsto (x,(\lambda_1(x)\prod_{j} z_j^{e_{1j}}, \dots, \lambda_n(x)\prod_{j} z_j^{e_{nj}})).\end{equation*}
\begin{equation*}(x,(z_1,\dots, z_n)) \mapsto (x,(\lambda_1(x)\prod_{j} z_j^{e_{1j}}, \dots, \lambda_n(x)\prod_{j} z_j^{e_{nj}})).\end{equation*}By definition of λi this map sends
and hence induces a morphism of blow-ups as quotients of subspaces of these bundles.
Since any morphism of log schemes is the composition of a strict morphism and a morphism given by the identity on underlying spaces these two cases are enough to define the analytification of an arbitrary map of log schemes.
One can verify that this definition of the analytification functor for DF log scheme agrees with the analytification of its associated log scheme originally introduced by Kato and Nakayama in [Reference Kato and Nakayama13]. This can be checked through direct computation but for a less tedious argument see [Reference Bergström, Diaconu, Petersen and Westerland4]. From section 3 onward we will drop the “DF” prefix and let “log scheme” mean “DF log scheme”. All log schemes referenced in this article will indeed be DF log schemes but because of the above the distinction is not important for our purposes anyway.
Remark. In [Reference Kato and Nakayama13], ![]() $\mathsf X^{\text{KN}}$ is also given an associated sheaf of rings which, provided that
$\mathsf X^{\text{KN}}$ is also given an associated sheaf of rings which, provided that ![]() $\underline{\mathsf X}$ is smooth and that the divisor associated to all non zero sections of line bundles is a smooth normal crossings divisor, gives
$\underline{\mathsf X}$ is smooth and that the divisor associated to all non zero sections of line bundles is a smooth normal crossings divisor, gives ![]() $X^{\text{KN}}$ the structure of a smooth real manifold with corners. This motivates the name “analytification”. These conditions are all satisfied for the log schemes we consider in this article and we could, with a little more work, replace the word “homeomorphism” with “diffeomorphism” in theorems 5.12 and 5.13.
$X^{\text{KN}}$ the structure of a smooth real manifold with corners. This motivates the name “analytification”. These conditions are all satisfied for the log schemes we consider in this article and we could, with a little more work, replace the word “homeomorphism” with “diffeomorphism” in theorems 5.12 and 5.13.
We will not need to use this explicit definition of the analytification of a morphism at any point in this article. Instead, all we will need is that the analytification of a map exists, is functorial, and satisfies the following properties:
• For a log scheme
 $\mathsf X$ with log structure
$\mathsf X$ with log structure  $\mathfrak L = (s_i\colon \mathcal O_{\underline{\mathsf X}} \to \mathcal L_i) _{1\leq i \leq n}$ the analytification of the map
$\mathfrak L = (s_i\colon \mathcal O_{\underline{\mathsf X}} \to \mathcal L_i) _{1\leq i \leq n}$ the analytification of the map  $\mathsf X \to \underline{\mathsf X}$ given by the identity on underlying schemes is the blow-down map
$\mathsf X \to \underline{\mathsf X}$ given by the identity on underlying schemes is the blow-down map
 \begin{equation*}\mathsf X^\text{KN} =~\mathrm{Bl}^{\mathbb{R}}_{\tilde s_n}~\mathrm{Bl}^{\mathbb{R}}_{\tilde s_{n-1}}\ \dots~\mathrm{Bl}^{\mathbb{R}}_{s_1}\ \underline{\mathsf X}(\mathbb C) \to \underline{\mathsf X}(\mathbb C).\end{equation*}
\begin{equation*}\mathsf X^\text{KN} =~\mathrm{Bl}^{\mathbb{R}}_{\tilde s_n}~\mathrm{Bl}^{\mathbb{R}}_{\tilde s_{n-1}}\ \dots~\mathrm{Bl}^{\mathbb{R}}_{s_1}\ \underline{\mathsf X}(\mathbb C) \to \underline{\mathsf X}(\mathbb C).\end{equation*}• For a strict morphism of log schemes
 $f\colon \mathsf X \to \mathsf Y$ the following is a Cartesian diagram:
$f\colon \mathsf X \to \mathsf Y$ the following is a Cartesian diagram:
Both of these properties are standard and easy to verify so we omit a proof and will use them freely without reference.
2.3. Virtual logarithmic geometry
In this section we will give a short introduction to virtual morphisms of log schemes which were introduced by Howell [Reference Howell12] and further studied by Dupont, Panzer, and Pym [Reference Dupont, Panzer and Pym8]. Such virtual morphisms will be irrelevant for most sections of this article but in section 5.4 we include a discussion on how one can generalize some of our results using virtual morphisms in ways that are not possible otherwise. In the language of normal, i.e. non DF, logarithmic geometry a log structure on a scheme ![]() $X$ is a sheaf of monoids
$X$ is a sheaf of monoids ![]() $\mathcal M$ with a morphism of sheaves of monoids
$\mathcal M$ with a morphism of sheaves of monoids ![]() $\alpha\colon \mathcal M \to \mathcal O_X$ which restricts to an isomorphism
$\alpha\colon \mathcal M \to \mathcal O_X$ which restricts to an isomorphism ![]() $\alpha^{-1}(\mathcal O_X^\times) \to \mathcal O_X^\times$. A map of log structures is then a map of sheaves of monoids over
$\alpha^{-1}(\mathcal O_X^\times) \to \mathcal O_X^\times$. A map of log structures is then a map of sheaves of monoids over ![]() $\mathcal O_X$,
$\mathcal O_X$, ![]() $\mathcal M_1 \to \mathcal M_2$. Note that such a map commutes with the maps from
$\mathcal M_1 \to \mathcal M_2$. Note that such a map commutes with the maps from ![]() $\mathcal O^\times$ by definition.
$\mathcal O^\times$ by definition.
A virtual morphism of log structures is a morphism of the groupifications ![]() $\mathcal M_1^{\text{gp}} \to \mathcal M_2^{\text{gp}}$ which makes the diagram
$\mathcal M_1^{\text{gp}} \to \mathcal M_2^{\text{gp}}$ which makes the diagram

commute. Note that the groupifications ![]() $\mathcal M_1^{\text{gp}}, \mathcal M_2^{\text{gp}}$ do not have maps to
$\mathcal M_1^{\text{gp}}, \mathcal M_2^{\text{gp}}$ do not have maps to ![]() $\mathcal O_X$ which is why we use this weaker condition. Also note that the category of virtual log structures has more morphisms but we define it to have the same objects as the category of log structures. For a short motivation regarding why it makes sense to introduce such virtual morphisms it is worth mentioning that the log Betti and log de Rham cohomology functors are well defined for log schemes with virtual morphisms and the same is also true for the Kato–Nakayama analytification functor.
$\mathcal O_X$ which is why we use this weaker condition. Also note that the category of virtual log structures has more morphisms but we define it to have the same objects as the category of log structures. For a short motivation regarding why it makes sense to introduce such virtual morphisms it is worth mentioning that the log Betti and log de Rham cohomology functors are well defined for log schemes with virtual morphisms and the same is also true for the Kato–Nakayama analytification functor.
Although Dupont, Panzer, and Pym do define virtual morphisms of DF log structures their definition of a DF log structure is different from ours. Thus, we give a somewhat different definition here.
Definition 2.7. A virtual morphism of DF log structures on a scheme ![]() $X$
$X$
is a collection ![]() $\{e_{ij}\}$ of integers together with isomorphisms of line bundles
$\{e_{ij}\}$ of integers together with isomorphisms of line bundles
 \begin{equation*}\mathcal L_i \xrightarrow{\cong} \bigotimes_{1\leq j \leq m}\mathcal M_j^{\otimes e_{ij}}\end{equation*}
\begin{equation*}\mathcal L_i \xrightarrow{\cong} \bigotimes_{1\leq j \leq m}\mathcal M_j^{\otimes e_{ij}}\end{equation*} for each ![]() $1\leq i \leq n$ satisfying the following if
$1\leq i \leq n$ satisfying the following if ![]() $s_i \neq 0$
$s_i \neq 0$
•
 $e_{ij}\geq 0$ for every j.
$e_{ij}\geq 0$ for every j.• the sections si are mapped to the corresponding sections
 $\bigotimes_{1\leq j \leq m}t_j^{\otimes e_{ij}}$
$\bigotimes_{1\leq j \leq m}t_j^{\otimes e_{ij}}$
Remark. Although the constructions are closely related, our category of DF log schemes and the category of log schemes in [Reference Dupont, Panzer and Pym8] are not equivalent categories nor are they subcategories of each other and thus this definition cannot be “derived” from that of Dupont, Panzer, and Pym in any meaningful way.
Remark. For non connected schemes this definition must be appropriately modified for sections that are identically zero on some, but not all, components.
The category of DF log schemes with virtual morphisms, ![]() ${}^{\text{\textbf{V}}}~\text{\textbf{DF-Log}}$ fits into a commutative diagram of categories:
${}^{\text{\textbf{V}}}~\text{\textbf{DF-Log}}$ fits into a commutative diagram of categories:

We will omit the construction of the functor ![]() ${}^{\text{\textbf{V}}}~\text{\textbf{DF-Log}}_X \to ^{\text{\textbf{V}}}~\text{\textbf{Log}}_X$ but the interested reader is encouraged to construct it themselves and/or verify that our definition of the Kato–Nakayama analytification functor is still well defined for virtual morphisms. Doing this hopefully sheds some light on why this definition is a reasonable one.
${}^{\text{\textbf{V}}}~\text{\textbf{DF-Log}}_X \to ^{\text{\textbf{V}}}~\text{\textbf{Log}}_X$ but the interested reader is encouraged to construct it themselves and/or verify that our definition of the Kato–Nakayama analytification functor is still well defined for virtual morphisms. Doing this hopefully sheds some light on why this definition is a reasonable one.
Example 2.8. There is no morphism of log schemes ![]() $\text{Spec } \mathbb{k} \to (\text{Spec } \mathbb{k} , 0\colon \mathcal O_{\mathbb{k}} \to \mathcal O_{\mathbb{k}})$ but there is such a morphism of virtual log schemes (one for each automorphism
$\text{Spec } \mathbb{k} \to (\text{Spec } \mathbb{k} , 0\colon \mathcal O_{\mathbb{k}} \to \mathcal O_{\mathbb{k}})$ but there is such a morphism of virtual log schemes (one for each automorphism ![]() $\mathcal O_{\mathbb{k}} \to \mathcal O_{\mathbb{k}}$). For
$\mathcal O_{\mathbb{k}} \to \mathcal O_{\mathbb{k}}$). For ![]() $\mathbb{k} = \mathbb C$, the Kato–Nakayama analytification of these maps are the inclusions of a point in
$\mathbb{k} = \mathbb C$, the Kato–Nakayama analytification of these maps are the inclusions of a point in ![]() $S^1$. Similarly, the group inverse map
$S^1$. Similarly, the group inverse map ![]() $i\colon S^1 \to S^1$ is not the analytification of any map of log schemes
$i\colon S^1 \to S^1$ is not the analytification of any map of log schemes ![]() $(\text{Spec } \mathbb C , 0\colon \mathcal O_{\mathbb{C}} \to \mathcal O_{\mathbb{C}}) \to (\text{Spec } \mathbb{k} , 0\colon \mathcal O_{\mathbb{C}} \to \mathcal O_{\mathbb{C}})$ but it is a virtual map of log schemes corresponding to the isomorphism
$(\text{Spec } \mathbb C , 0\colon \mathcal O_{\mathbb{C}} \to \mathcal O_{\mathbb{C}}) \to (\text{Spec } \mathbb{k} , 0\colon \mathcal O_{\mathbb{C}} \to \mathcal O_{\mathbb{C}})$ but it is a virtual map of log schemes corresponding to the isomorphism  $\mathcal O_{\mathbb{C}} \cong \mathcal O^{\otimes (-1)}_{\mathbb{C}}$.
$\mathcal O_{\mathbb{C}} \cong \mathcal O^{\otimes (-1)}_{\mathbb{C}}$.
Example 2.9. Let ![]() $X$ be a smooth scheme and let
$X$ be a smooth scheme and let ![]() $D$ be a smooth effective Cartier divisor. By definition
$D$ be a smooth effective Cartier divisor. By definition
 \begin{equation*}(X, s_D\colon \mathcal O_X \to \mathcal O_X(D))^\text{KN} =~\mathrm{Bl}^{\mathbb{R}}_{D(\mathbb C)}\ X(\mathbb C).\end{equation*}
\begin{equation*}(X, s_D\colon \mathcal O_X \to \mathcal O_X(D))^\text{KN} =~\mathrm{Bl}^{\mathbb{R}}_{D(\mathbb C)}\ X(\mathbb C).\end{equation*} By our definition of the real oriented blow-up there is an embedding of  $\mathrm{Bl}^{\mathbb{R}}_{D(\mathbb C)}\ X(\mathbb C)$, into the unit circle bundle of (the analytification of)
$\mathrm{Bl}^{\mathbb{R}}_{D(\mathbb C)}\ X(\mathbb C)$, into the unit circle bundle of (the analytification of) ![]() $\mathcal O_X(D)$ with some arbitrarily chosen metric. This unit circle bundle is, again by definition, the KN analytification of
$\mathcal O_X(D)$ with some arbitrarily chosen metric. This unit circle bundle is, again by definition, the KN analytification of ![]() $(X, 0\colon \mathcal O_X \to \mathcal O_X(D))$. The inclusion
$(X, 0\colon \mathcal O_X \to \mathcal O_X(D))$. The inclusion
is not the analytification of any map of log schemes since the zero section cannot be pulled back to a non zero section. It is however the analytification of a virtual map given by the identity on both underlying spaces and ![]() $\mathcal O_X(D) \to \mathcal O_X(D)^{\otimes 1}$.
$\mathcal O_X(D) \to \mathcal O_X(D)^{\otimes 1}$.
3. Topological Fulton–MacPherson and Kontsevich spaces
In this section we recall the topological Fulton–MacPherson spaces, ![]() $\text{FM}^\text{top}_n(\mathbb R^D)$, and the closely related Kontsevich spaces,
$\text{FM}^\text{top}_n(\mathbb R^D)$, and the closely related Kontsevich spaces, ![]() $\text{K}_{D,n} \cong~\text{FM}^\text{top}_n(\mathbb R^D)\big /\mathbb R_{ \gt 0} \lt imes \mathbb R^D$.
$\text{K}_{D,n} \cong~\text{FM}^\text{top}_n(\mathbb R^D)\big /\mathbb R_{ \gt 0} \lt imes \mathbb R^D$.
3.1. The Fulton–MacPherson compactification of a manifold
Let ![]() $X$ be a smooth manifold, let n be a positive integer and let
$X$ be a smooth manifold, let n be a positive integer and let ![]() $P_2({n})$, denote the set of subsets of
$P_2({n})$, denote the set of subsets of ![]() $[n]$ with at least 2 elements. For a set
$[n]$ with at least 2 elements. For a set ![]() $I\in P_2({n})$ let
$I\in P_2({n})$ let ![]() $\Delta_I$ denote the corresponding diagonal in
$\Delta_I$ denote the corresponding diagonal in ![]() $X^n$, i.e.
$X^n$, i.e.
By abuse of notation we will also use ![]() $\Delta_I$ to denote the (small) diagonal in
$\Delta_I$ to denote the (small) diagonal in ![]() $X^I$.
$X^I$.
Definition 3.1. The Fulton–MacPherson compactification, ![]() $\text{FM}^\text{top}_n(X)$ is the closure of the image of the map
$\text{FM}^\text{top}_n(X)$ is the closure of the image of the map
 \begin{equation*}\text{Conf} _n(X) \hookrightarrow \prod_{I\in P_2({n})}~\mathrm{Bl}^{\mathbb{R}}_{\Delta_I}\ X^I.\end{equation*}
\begin{equation*}\text{Conf} _n(X) \hookrightarrow \prod_{I\in P_2({n})}~\mathrm{Bl}^{\mathbb{R}}_{\Delta_I}\ X^I.\end{equation*} We let  $f_I\colon~\text{FM}^\text{top}_n(X) \to~\mathrm{Bl}^{\mathbb{R}}_{\Delta_I}\ (X)$ denote the restrictionof the corresponding projection to
$f_I\colon~\text{FM}^\text{top}_n(X) \to~\mathrm{Bl}^{\mathbb{R}}_{\Delta_I}\ (X)$ denote the restrictionof the corresponding projection to ![]() $\text{FM}^\text{top}_n(X)$ and we let
$\text{FM}^\text{top}_n(X)$ and we let ![]() $\rho\colon~\text{FM}^\text{top}_n(X) \to X^n$ denote the surjective extension of the embedding
$\rho\colon~\text{FM}^\text{top}_n(X) \to X^n$ denote the surjective extension of the embedding ![]() $\text{Conf} _n(X) \hookrightarrow X^n$ to
$\text{Conf} _n(X) \hookrightarrow X^n$ to ![]() $\text{FM}^\text{top}_n(X)$.
$\text{FM}^\text{top}_n(X)$.
Remark. This definition is the one used by Axelrod and Singer in [Reference Axelrod and Singer2] but many sources use a different definition of the topological Fulton–MacPherson compactification introduced by Sinha [Reference Sinha25]. These can easily be shown to be equivalent.
Definition 3.2. The Kontsevich space of n points in dimension d, ![]() $\text{K}_{D,n}$, is defined as the fibre
$\text{K}_{D,n}$, is defined as the fibre ![]() $\rho^{-1}((0,0,\dots,0)) \subseteq~\text{FM}^\text{top}_n(\mathbb R^D)$.
$\rho^{-1}((0,0,\dots,0)) \subseteq~\text{FM}^\text{top}_n(\mathbb R^D)$.
Remark. It is more common to define ![]() $\text{K}_{D,n}$ as
$\text{K}_{D,n}$ as ![]() $\text{FM}^\text{top}_m(\mathbb R^D)\big / \mathbb R_{ \gt 0} \lt imes \mathbb R^D$ but one can show that the composition
$\text{FM}^\text{top}_m(\mathbb R^D)\big / \mathbb R_{ \gt 0} \lt imes \mathbb R^D$ but one can show that the composition ![]() $\rho^{-1}((0,0,\dots,0)) \hookrightarrow~\text{FM}^\text{top}_n(\mathbb R^D) \to~\text{FM}^\text{top}_m(\mathbb R^D)\big / \mathbb R_{ \gt 0} \lt imes \mathbb R^D$ is an isomorphism and this equivalent definition will be more useful for our purposes.
$\rho^{-1}((0,0,\dots,0)) \hookrightarrow~\text{FM}^\text{top}_n(\mathbb R^D) \to~\text{FM}^\text{top}_m(\mathbb R^D)\big / \mathbb R_{ \gt 0} \lt imes \mathbb R^D$ is an isomorphism and this equivalent definition will be more useful for our purposes.
The fibre over the origin of  $\mathrm{Bl}^{\mathbb{R}}_{\Delta_I}\ (\mathbb R^D)^I$ is
$\mathrm{Bl}^{\mathbb{R}}_{\Delta_I}\ (\mathbb R^D)^I$ is ![]() $S^{D(\vert I \vert-1)-1}$. Thus,
$S^{D(\vert I \vert-1)-1}$. Thus,  $f_I\colon~\text{FM}^\text{top}_n(\mathbb R^D) \to~\mathrm{Bl}^{\mathbb{R}}_{\Delta_I}\ (\mathbb R^D)^I$ restricts to a map
$f_I\colon~\text{FM}^\text{top}_n(\mathbb R^D) \to~\mathrm{Bl}^{\mathbb{R}}_{\Delta_I}\ (\mathbb R^D)^I$ restricts to a map  $\pi_I\colon~\text{K}_{D,n} \to S^{D(\vert I \vert-1)-1}$. These maps give a closed embedding
$\pi_I\colon~\text{K}_{D,n} \to S^{D(\vert I \vert-1)-1}$. These maps give a closed embedding
 \begin{equation*}\text{K}_{D,n} \hookrightarrow \prod_{I\in P_2({n})}S^{D(\vert I \vert-1)-1},\end{equation*}
\begin{equation*}\text{K}_{D,n} \hookrightarrow \prod_{I\in P_2({n})}S^{D(\vert I \vert-1)-1},\end{equation*} i.e. an element ![]() $x\in~\text{K}_{D,n}$ is uniquely determined by its components
$x\in~\text{K}_{D,n}$ is uniquely determined by its components ![]() $x_I = \pi_I(x)$.
$x_I = \pi_I(x)$.
Note that while we have chosen to use ![]() $[n] = \{1,\dots,n\}$ as coordinate indices in the definitions above we could have used any (finite) index set N instead. We can thus define
$[n] = \{1,\dots,n\}$ as coordinate indices in the definitions above we could have used any (finite) index set N instead. We can thus define  $\text{FM}^\text{top}_N(X)$ and
$\text{FM}^\text{top}_N(X)$ and ![]() $\text{K}_{d,N}$ with maps
$\text{K}_{d,N}$ with maps  $\rho\colon~\text{FM}^\text{top}_N(X)\to X^N$,
$\rho\colon~\text{FM}^\text{top}_N(X)\to X^N$,  $f_{I}\colon~\text{FM}^\text{top}_N(X) \to~\mathrm{Bl}^{\mathbb{R}}_{\Delta_I}\ (X)^I$, and
$f_{I}\colon~\text{FM}^\text{top}_N(X) \to~\mathrm{Bl}^{\mathbb{R}}_{\Delta_I}\ (X)^I$, and  $\pi_{I}\colon~\text{K}_{D,N} \to S^{D(\vert I \vert-1)-1}$ in the analogous way. Here
$\pi_{I}\colon~\text{K}_{D,N} \to S^{D(\vert I \vert-1)-1}$ in the analogous way. Here ![]() $I$ is a subset of
$I$ is a subset of ![]() $N$.
$N$.
3.2. The Fulton–MacPherson operad
For a fixed dimension D the collection ![]() $ \{\text{K}_{D,n}\} _{n\in \mathbb N}$ can be given the structure of a topological operad as follows.
$ \{\text{K}_{D,n}\} _{n\in \mathbb N}$ can be given the structure of a topological operad as follows.
The permutation action of ![]() $\Sigma_n$ on
$\Sigma_n$ on ![]() $\text{Conf} _n(\mathbb R^D)$ extends to a free action on
$\text{Conf} _n(\mathbb R^D)$ extends to a free action on ![]() $\text{FM}^\text{top}_n(\mathbb R^D)$ which gives an induced action on the fibre over the origin,
$\text{FM}^\text{top}_n(\mathbb R^D)$ which gives an induced action on the fibre over the origin, ![]() $\text{K}_{D,n}$. This is the symmetry action of the operad.
$\text{K}_{D,n}$. This is the symmetry action of the operad.
Next, any surjection ![]() $\varphi \colon I\twoheadrightarrow J$ of sets induces a monomorphism
$\varphi \colon I\twoheadrightarrow J$ of sets induces a monomorphism ![]() $(\mathbb R^D)^J \hookrightarrow (\mathbb R^D)^I$ such that the inverse image of
$(\mathbb R^D)^J \hookrightarrow (\mathbb R^D)^I$ such that the inverse image of ![]() $\Delta_I$ is
$\Delta_I$ is ![]() $\Delta_J$. This gives a map
$\Delta_J$. This gives a map  $\mathrm{Bl}^{\mathbb{R}}_{\Delta_J}\ (\mathbb R^D)^J\to~\mathrm{Bl}^{\mathbb{R}}_{\Delta_I}\ (\mathbb R^D)^I$ which restricts to a map of fibres over the origin
$\mathrm{Bl}^{\mathbb{R}}_{\Delta_J}\ (\mathbb R^D)^J\to~\mathrm{Bl}^{\mathbb{R}}_{\Delta_I}\ (\mathbb R^D)^I$ which restricts to a map of fibres over the origin
 \begin{equation*}g_\varphi\colon S^{D(\vert J \vert-1)-1} \to S^{D(\vert I \vert-1)-1}.\end{equation*}
\begin{equation*}g_\varphi\colon S^{D(\vert J \vert-1)-1} \to S^{D(\vert I \vert-1)-1}.\end{equation*} Let ![]() $q\colon M\twoheadrightarrow [n]$ be a surjection of finite sets. By abuse of notation we will also let q denote the restriction of this function
$q\colon M\twoheadrightarrow [n]$ be a surjection of finite sets. By abuse of notation we will also let q denote the restriction of this function ![]() $I\twoheadrightarrow q(I)$ for any
$I\twoheadrightarrow q(I)$ for any ![]() $I \subseteq M$. The above construction allows us to define a map
$I \subseteq M$. The above construction allows us to define a map
 \begin{equation*}\gamma\colon~\text{K}_{D,[n]} \times \prod_{i\in [n]}~\text{K}_{D,q^{-1}(i)} \to~\text{K}_{d,M}\end{equation*}
\begin{equation*}\gamma\colon~\text{K}_{D,[n]} \times \prod_{i\in [n]}~\text{K}_{D,q^{-1}(i)} \to~\text{K}_{d,M}\end{equation*}by
 \begin{equation*}\gamma(x,y^1,\dots,y^n)_I = \begin{cases}
y^i_I & I \subseteq q^{-1}(i)\\
g_q(x_{q(I)}) &~\text{else}
\end{cases}.\end{equation*}
\begin{equation*}\gamma(x,y^1,\dots,y^n)_I = \begin{cases}
y^i_I & I \subseteq q^{-1}(i)\\
g_q(x_{q(I)}) &~\text{else}
\end{cases}.\end{equation*}This defines the composition maps of the operad.
Remark. We use the standard notation for an operad defined in terms of finite sets here. See for example [Reference Markl, Stasheff and Shnider20, Part II, section 1.7] for an introduction to the notation.
Finally, ![]() $\text{K}_{d,1}$ is the one point space so there is only one choice for the identity map,
$\text{K}_{d,1}$ is the one point space so there is only one choice for the identity map, ![]() $\eta\colon * \to~\text{K}_{d,1}$. The operad axioms can be verified manually for this collection of maps.
$\eta\colon * \to~\text{K}_{d,1}$. The operad axioms can be verified manually for this collection of maps.
Definition 3.3. We call the operad with spaces ![]() $ \{\text{K}_{D,n}\} $ (for a fixed D) and the above composition, symmetry, and identity maps the Fulton–MacPherson operad in dimension D, denoted
$ \{\text{K}_{D,n}\} $ (for a fixed D) and the above composition, symmetry, and identity maps the Fulton–MacPherson operad in dimension D, denoted ![]() $\text{\textbf{FM}}_D$.
$\text{\textbf{FM}}_D$.
By a result of Salvatore, the Fulton–MacPherson operad is weakly equivalent to the operad of little d-dimensional disks [Reference Salvatore23, proposition 3.9].
The action of ![]() $\text{SO}(D)$ on
$\text{SO}(D)$ on ![]() $\mathbb R^D$ induces an action on
$\mathbb R^D$ induces an action on ![]() $\text{Conf} _n(\mathbb R^D)$ which extends to
$\text{Conf} _n(\mathbb R^D)$ which extends to ![]() $\text{FM}^\text{top}_n(\mathbb R^D)$. Since all rotations map the zero vector to itself this restricts to an action on the fibre
$\text{FM}^\text{top}_n(\mathbb R^D)$. Since all rotations map the zero vector to itself this restricts to an action on the fibre ![]() $\text{K}_{D,n}$. One can check that this gives an action by
$\text{K}_{D,n}$. One can check that this gives an action by ![]() $\text{SO}(D)$ on the
$\text{SO}(D)$ on the ![]() $\text{\textbf{FM}}_D$ operad in the sense of [Reference Salvatore and Wahl24]. Furthermore the weak equivalence
$\text{\textbf{FM}}_D$ operad in the sense of [Reference Salvatore and Wahl24]. Furthermore the weak equivalence ![]() $\text{\textbf{FM}}_D \sim~\text{\textbf{LD}}_D$ can be shown to commute with this action which gives a weak equivalence between
$\text{\textbf{FM}}_D \sim~\text{\textbf{LD}}_D$ can be shown to commute with this action which gives a weak equivalence between ![]() $\text{\textbf{FM}}_D\rtimes~\text{SO}(D)$ and
$\text{\textbf{FM}}_D\rtimes~\text{SO}(D)$ and ![]() $\text{\textbf{LD}}_D \rtimes~\text{SO}(D)$, the framed little disks operad.
$\text{\textbf{LD}}_D \rtimes~\text{SO}(D)$, the framed little disks operad.
With the notable exception of the case D = 2, the framed little disks operad is, however, not the operad studied in this article. Instead we are interested in the following construction. When the dimension is an even number ![]() $D = 2d$ there is an embedding of topological groups
$D = 2d$ there is an embedding of topological groups
 \begin{equation*}S^1\cong U(1)\stackrel{diag.}{\hookrightarrow}U(d)\hookrightarrow \text{SO}(2d)\end{equation*}
\begin{equation*}S^1\cong U(1)\stackrel{diag.}{\hookrightarrow}U(d)\hookrightarrow \text{SO}(2d)\end{equation*} This induces an action of S 1 on the ![]() $\text{\textbf{FM}}_{2d}$ operad and we can form the semidirect product
$\text{\textbf{FM}}_{2d}$ operad and we can form the semidirect product ![]() $\text{\textbf{FM}}_{2d} \rtimes S^1$.
$\text{\textbf{FM}}_{2d} \rtimes S^1$.
The main goal of this article is to construct a (non-unital) operad of log schemes whose Kato–Nakayama analytification is ![]() $\text{\textbf{FM}}_{2d}\rtimes S^1$ which is weakly equivalent to the S 1-framed little disks operad.
$\text{\textbf{FM}}_{2d}\rtimes S^1$ which is weakly equivalent to the S 1-framed little disks operad.
4. The Chen, Gibney, Krashen operad
Fix a base field ![]() $\mathbb{k}$ for the remainder of the article. In this section we recall the definition of the moduli spaces of stable n-pointed rooted trees of d-dimensional projective spaces,
$\mathbb{k}$ for the remainder of the article. In this section we recall the definition of the moduli spaces of stable n-pointed rooted trees of d-dimensional projective spaces, ![]() $T_{d,n}$, and describe an operad of (smooth)
$T_{d,n}$, and describe an operad of (smooth) ![]() $\mathbb{k}$-varieties with spaces
$\mathbb{k}$-varieties with spaces ![]() $T_{d,n}$ for a fixed d which generalizes the operad of pointed stable curves of genus 0. For a more in depth description of the spaces
$T_{d,n}$ for a fixed d which generalizes the operad of pointed stable curves of genus 0. For a more in depth description of the spaces ![]() $T_{d,n}$, including a definition of a rooted tree of projective spaces, see [Reference Chen, Gibney and Krashen5].
$T_{d,n}$, including a definition of a rooted tree of projective spaces, see [Reference Chen, Gibney and Krashen5].
4.1. Fulton–MacPherson compactifications
Let us recall some important aspects of the Fulton–MacPherson compactification [Reference Fulton and MacPherson9]. Let ![]() $X$ be a smooth
$X$ be a smooth ![]() $\mathbb{k}$-variety. For an integer n and a subset
$\mathbb{k}$-variety. For an integer n and a subset ![]() $I \subseteq [n]$ with
$I \subseteq [n]$ with ![]() $\vert I \vert\geq 2$ let
$\vert I \vert\geq 2$ let ![]() $\mathcal I_I$ denote the sheaf of ideals on
$\mathcal I_I$ denote the sheaf of ideals on ![]() $X^n$ corresponding to the
$X^n$ corresponding to the ![]() $I$-diagonal,
$I$-diagonal, ![]() $\Delta_I \subseteq X^n$. Recall that we denote the set of subsets of
$\Delta_I \subseteq X^n$. Recall that we denote the set of subsets of ![]() $[n]$ with at least 2 elements by
$[n]$ with at least 2 elements by ![]() $P_2({n})$.
$P_2({n})$.
Let ![]() $\rho\colon~\text{FM}^{\text{alg}}_n(X) \to X^n$ denote the Fulton–MacPherson compactification of
$\rho\colon~\text{FM}^{\text{alg}}_n(X) \to X^n$ denote the Fulton–MacPherson compactification of ![]() $\text{Conf} _n(X)$. We call this a “compactification” of
$\text{Conf} _n(X)$. We call this a “compactification” of ![]() $\text{Conf} _n(X)$ since ρ restricted to
$\text{Conf} _n(X)$ since ρ restricted to ![]() $\rho^{-1}(\text{Conf} _n(X))$ is an isomorphism and
$\rho^{-1}(\text{Conf} _n(X))$ is an isomorphism and ![]() $\text{FM}^{\text{alg}}_n(X)$ is compact provided that
$\text{FM}^{\text{alg}}_n(X)$ is compact provided that ![]() $X$ is. The remainder of this section will be dedicated to recalling some important results relating to the Fulton–MacPherson compactification. First, we just state the following facts, all of which can be found with proofs in [Reference Fulton and MacPherson9].
$X$ is. The remainder of this section will be dedicated to recalling some important results relating to the Fulton–MacPherson compactification. First, we just state the following facts, all of which can be found with proofs in [Reference Fulton and MacPherson9].
• The scheme
 $\text{FM}^{\text{alg}}_n(X)$ is a smooth variety.
$\text{FM}^{\text{alg}}_n(X)$ is a smooth variety.• There is an ordering of the elements in
 $P_2({n})$, such that
$P_2({n})$, such that  $\rho \colon~\text{FM}^{\text{alg}}_n(X) \to X^n$ is given by a sequence of blow-ups where we start with
$\rho \colon~\text{FM}^{\text{alg}}_n(X) \to X^n$ is given by a sequence of blow-ups where we start with  $X^n$ and at step t of the sequence we blow-up in the dominant transform of the tth diagonal through all previous blow-ups.
$X^n$ and at step t of the sequence we blow-up in the dominant transform of the tth diagonal through all previous blow-ups.• The closed subset
 $D(I) \subseteq~\text{FM}^{\text{alg}}_n(X)$ given by the dominant transform of
$D(I) \subseteq~\text{FM}^{\text{alg}}_n(X)$ given by the dominant transform of  $\Delta(X)$ through all these blow-ups is a smooth, effective Cartier divisor.
$\Delta(X)$ through all these blow-ups is a smooth, effective Cartier divisor.• The divisors
 $D(I)$ form a strict normal crossings divisor, i.e. any set of the divisors meets transversely.
$D(I)$ form a strict normal crossings divisor, i.e. any set of the divisors meets transversely.• The intersection
 $D(I_1,\dots, I_k):= D(I_1) \cap \dots \cap D(I_k)$ is non-empty if and only if the sets
$D(I_1,\dots, I_k):= D(I_1) \cap \dots \cap D(I_k)$ is non-empty if and only if the sets  $I_1, \dots, I_k$ are nested i.e. for each
$I_1, \dots, I_k$ are nested i.e. for each  $i,j$ we have
$i,j$ we have  $I_i \subseteq I_j$,
$I_i \subseteq I_j$,  $I_j \subseteq I_i$ or
$I_j \subseteq I_i$ or  $I_i\cap I_j = \emptyset$.
$I_i\cap I_j = \emptyset$.• We have
 $\text{FM}^{\text{alg}}_n(X) \setminus~\text{Conf} _n(X) = \bigcup_{I \in P_2({n})} D(I)$.
$\text{FM}^{\text{alg}}_n(X) \setminus~\text{Conf} _n(X) = \bigcup_{I \in P_2({n})} D(I)$.• We have that
 $\rho^{-1}(\Delta(I)) = \bigcup_{I \subseteq I'} D(I')$, i.e. the pullback of the ideal inclusion
$\rho^{-1}(\Delta(I)) = \bigcup_{I \subseteq I'} D(I')$, i.e. the pullback of the ideal inclusion  $\mathcal I_I \hookrightarrow \mathcal O_{X^n}$ factors via a quotient
$\mathcal I_I \hookrightarrow \mathcal O_{X^n}$ factors via a quotient
 \begin{equation*}\rho^* \mathcal I_I \twoheadrightarrow \prod_{I \subseteq I'} \mathcal I_{D(I')} \cong \bigotimes_{I \subseteq I'} \mathcal O_{\text{FM}^{\text{alg}}_n(X)}(-D(I')).\end{equation*}
\begin{equation*}\rho^* \mathcal I_I \twoheadrightarrow \prod_{I \subseteq I'} \mathcal I_{D(I')} \cong \bigotimes_{I \subseteq I'} \mathcal O_{\text{FM}^{\text{alg}}_n(X)}(-D(I')).\end{equation*}• The composition
 $\text{FM}^{\text{alg}}_n(X) \to X^n \to X^I$ factors as
$\text{FM}^{\text{alg}}_n(X) \to X^n \to X^I$ factors as  $\text{FM}^{\text{alg}}_n(X) \xrightarrow{f_I}~\mathrm{Bl}_{\Delta_I}\ X^I \xrightarrow{\rho_I} X^I,$ where ρI is the blow-down map.
$\text{FM}^{\text{alg}}_n(X) \xrightarrow{f_I}~\mathrm{Bl}_{\Delta_I}\ X^I \xrightarrow{\rho_I} X^I,$ where ρI is the blow-down map.
Remark. Recall that for a blow-up ![]() $\mathrm{Bl}_{Y}\ X \to X$ the dominant transform of a closed subscheme
$\mathrm{Bl}_{Y}\ X \to X$ the dominant transform of a closed subscheme ![]() $Z\subseteq X$ is defined as the strict transform of
$Z\subseteq X$ is defined as the strict transform of ![]() $Z$ if
$Z$ if ![]() $Z\not\subseteq Y$ and the pullback of
$Z\not\subseteq Y$ and the pullback of ![]() $Z$ to
$Z$ to ![]() $\mathrm{Bl}_{Y}\ X$ if
$\mathrm{Bl}_{Y}\ X$ if ![]() $Z\subseteq Y$.
$Z\subseteq Y$.
Note that by the last two points we have that if ![]() $E_{\Delta_I} \subseteq~\mathrm{Bl}_{\Delta_I}\ X^I$ denotes the exceptional divisor then there is an isomorphism
$E_{\Delta_I} \subseteq~\mathrm{Bl}_{\Delta_I}\ X^I$ denotes the exceptional divisor then there is an isomorphism
 \begin{equation*}f_I^* \mathcal O(E_{\Delta_I}) \cong \bigotimes_{I \subseteq I'} \mathcal O_{\text{FM}^{\text{alg}}_n(X)}(D(I'))\end{equation*}
\begin{equation*}f_I^* \mathcal O(E_{\Delta_I}) \cong \bigotimes_{I \subseteq I'} \mathcal O_{\text{FM}^{\text{alg}}_n(X)}(D(I'))\end{equation*}which sends corresponding sections to each other.
In addition to this geometric description of ![]() $\text{FM}^{\text{alg}}_n(X)$ there is also a functorial description which we will make great use of in this article.
$\text{FM}^{\text{alg}}_n(X)$ there is also a functorial description which we will make great use of in this article.
Definition 4.1. A screen on a scheme ![]() $H$ is a map
$H$ is a map ![]() $f\colon H \to X^n$ together with the following data
$f\colon H \to X^n$ together with the following data
• an invertible quotient
 $f^* \mathcal I_{I} \twoheadrightarrow \mathcal L_I$ for each
$f^* \mathcal I_{I} \twoheadrightarrow \mathcal L_I$ for each  $I\in P_2({n})$
$I\in P_2({n})$• a map
 $\mathcal L_I \to \mathcal L_J$ for each
$\mathcal L_I \to \mathcal L_J$ for each  $I \subseteq J$
$I \subseteq J$
such that the following diagram commutes for every ![]() $I \subseteq J$
$I \subseteq J$

where ![]() $f^*\mathcal I_I \to f^* \mathcal I_J$ is the pullback of the corresponding inclusion.
$f^*\mathcal I_I \to f^* \mathcal I_J$ is the pullback of the corresponding inclusion.
We say a screen satisfies the ![]() $I$-vanishing property for some
$I$-vanishing property for some ![]() $I\in P_2({n})$ if
$I\in P_2({n})$ if ![]() $\text{pr}_i\circ f\colon H \to X =~\text{pr}_j\circ f\colon H \to X$ for each
$\text{pr}_i\circ f\colon H \to X =~\text{pr}_j\circ f\colon H \to X$ for each ![]() $i,j\in I$ and, for every
$i,j\in I$ and, for every ![]() $J\in P_2({n})$, if
$J\in P_2({n})$, if ![]() $J\not \subseteq I$ and
$J\not \subseteq I$ and ![]() $\vert I\cap J \vert \geq 2$ then
$\vert I\cap J \vert \geq 2$ then ![]() $\mathcal L_{I\cap J}\to \mathcal L_J$ is the zero morphism.
$\mathcal L_{I\cap J}\to \mathcal L_J$ is the zero morphism.
We can define a screen on ![]() $\text{FM}^{\text{alg}}_n(X)$ by taking
$\text{FM}^{\text{alg}}_n(X)$ by taking ![]() $f=\rho$,
$f=\rho$,  $\mathcal L_I = \bigotimes_{I \subseteq I'}\mathcal O_{\text{FM}^{\text{alg}}_n(X)}(-D(I'))$ and letting the invertible quotients be the maps
$\mathcal L_I = \bigotimes_{I \subseteq I'}\mathcal O_{\text{FM}^{\text{alg}}_n(X)}(-D(I'))$ and letting the invertible quotients be the maps
 \begin{equation*}\rho^*\mathcal I_I \twoheadrightarrow \bigotimes_{I \subseteq I'}\mathcal O_{\text{FM}^{\text{alg}}_n(X)}(-D(I')).\end{equation*}
\begin{equation*}\rho^*\mathcal I_I \twoheadrightarrow \bigotimes_{I \subseteq I'}\mathcal O_{\text{FM}^{\text{alg}}_n(X)}(-D(I')).\end{equation*} The maps ![]() $\mathcal L_{I} \to \mathcal L_J$ here are induced by the ideal inclusions
$\mathcal L_{I} \to \mathcal L_J$ here are induced by the ideal inclusions  $\mathcal O_{\text{FM}^{\text{alg}}_n(X)}(-D(I))\hookrightarrow \mathcal O_{\text{FM}^{\text{alg}}_n(X)}$. We call this screen the universal screen on
$\mathcal O_{\text{FM}^{\text{alg}}_n(X)}(-D(I))\hookrightarrow \mathcal O_{\text{FM}^{\text{alg}}_n(X)}$. We call this screen the universal screen on ![]() $\text{FM}^{\text{alg}}_n(X)$.
$\text{FM}^{\text{alg}}_n(X)$.
Definition 4.2. Let ![]() $\mathcal{X}_n\colon~\text{\textbf{{Sch}}}^{op} \to ~\text{\textbf{Set}}$ be the functor which sends a scheme
$\mathcal{X}_n\colon~\text{\textbf{{Sch}}}^{op} \to ~\text{\textbf{Set}}$ be the functor which sends a scheme ![]() $H$ to the set of screens on
$H$ to the set of screens on ![]() $H$ up to isomorphism of the screen data.
$H$ up to isomorphism of the screen data.
Similarly let ![]() $\mathcal{X}(I_1,\dots,I_k)$ denote the subfunctor sending
$\mathcal{X}(I_1,\dots,I_k)$ denote the subfunctor sending ![]() $H$ to the set of screens on
$H$ to the set of screens on ![]() $H$ up to isomorphism which satisfy the Ir-vanishing property for each
$H$ up to isomorphism which satisfy the Ir-vanishing property for each ![]() $1\leq r \leq k$.
$1\leq r \leq k$.
Proposition 4.3. The Fulton–MacPherson compactification ![]() $\text{FM}^{\text{alg}}_n(X)$ represents the functor
$\text{FM}^{\text{alg}}_n(X)$ represents the functor ![]() $\mathcal{X}_n$. Furthermore, the natural isomorphism
$\mathcal{X}_n$. Furthermore, the natural isomorphism ![]() $\hom(-,\text{FM}^{\text{alg}}_n(X)) \to \mathcal{X}_n$ is given by sending the element
$\hom(-,\text{FM}^{\text{alg}}_n(X)) \to \mathcal{X}_n$ is given by sending the element ![]() $f\colon H \to~\text{FM}^{\text{alg}}_n(X)$ to the pullback to
$f\colon H \to~\text{FM}^{\text{alg}}_n(X)$ to the pullback to ![]() $H$ of the universal screen on
$H$ of the universal screen on ![]() $\text{FM}^{\text{alg}}_n(X)$ described above.
$\text{FM}^{\text{alg}}_n(X)$ described above.
Similarly ![]() $D(I_1,\dots, I_k) \subseteq~\text{FM}^{\text{alg}}_n(X)$ represents
$D(I_1,\dots, I_k) \subseteq~\text{FM}^{\text{alg}}_n(X)$ represents ![]() $\mathcal{X}(I_1,\dots, I_k)$. The natural isomorphism is given in the same way here as above.
$\mathcal{X}(I_1,\dots, I_k)$. The natural isomorphism is given in the same way here as above.
Proof. This is theorem 4 in [Reference Fulton and MacPherson9].
4.2. Pointed rooted trees of projective spaces
Chen, Gibney, and Krashen [Reference Chen, Gibney and Krashen5] introduced stable pointed rooted trees of projective spaces as a higher-dimensional analogue of stable pointed rational curves, and showed that ![]() $T_{d,n}$ (defined in section 4.3) is the moduli space of stable rooted n-pointed trees of d-dimensional projective spaces. Here we recall the definition and describe the morphisms in the operad
$T_{d,n}$ (defined in section 4.3) is the moduli space of stable rooted n-pointed trees of d-dimensional projective spaces. Here we recall the definition and describe the morphisms in the operad ![]() $\text{\textbf{CGK}}_d$ (defined in section 4.3), with
$\text{\textbf{CGK}}_d$ (defined in section 4.3), with ![]() $\text{\textbf{CGK}}_d(n) =T_{d,n}$ in terms of natural operations on such trees. The discussion is intended to convey geometric intuition for section 4.3, and we therefore suppress most proofs and technical details.
$\text{\textbf{CGK}}_d(n) =T_{d,n}$ in terms of natural operations on such trees. The discussion is intended to convey geometric intuition for section 4.3, and we therefore suppress most proofs and technical details.
Definition 4.4. A rooted tree of d-dimensional projective spaces is a connected, reduced, projective scheme ![]() $T$ with a closed embedding
$T$ with a closed embedding ![]() $r_0\colon \mathbb P^{d-1} \hookrightarrow T$, called the root hyperplane, obtained by the following finite inductive process:
$r_0\colon \mathbb P^{d-1} \hookrightarrow T$, called the root hyperplane, obtained by the following finite inductive process:
1. Start with
 $T \cong \mathbb{P}^d$ and choose a hyperplane embedding
$T \cong \mathbb{P}^d$ and choose a hyperplane embedding
 \begin{equation*}r_0 \colon \mathbb{P}^{d-1} \hookrightarrow T.\end{equation*}
\begin{equation*}r_0 \colon \mathbb{P}^{d-1} \hookrightarrow T.\end{equation*}This embedding is the root hyperplane.
2. Given a tree of d-dimensional projective spaces T produced in a previous step, choose a smooth point
 $x \in T$ disjoint from the singular locus and the root hyperplane
$x \in T$ disjoint from the singular locus and the root hyperplane  $r_0\colon \mathbb P^{d-1} \hookrightarrow T$. The next iteration
$r_0\colon \mathbb P^{d-1} \hookrightarrow T$. The next iteration  $T$ʹ is defined by forming the blow-up
$T$ʹ is defined by forming the blow-up  $\mathrm{Bl}_{x}\ T$ and gluing along its exceptional divisor
$\mathrm{Bl}_{x}\ T$ and gluing along its exceptional divisor  $\mathbb{P}^{d-1}$ a new copy of
$\mathbb{P}^{d-1}$ a new copy of  $\mathbb{P}^d$ along some hyperplane
$\mathbb{P}^d$ along some hyperplane  $\mathbb{P}^{d-1} \subseteq \mathbb{P}^d.$ Since x was chosen to be disjoint from the root hyperplane r 0 induces an embedding
$\mathbb{P}^{d-1} \subseteq \mathbb{P}^d.$ Since x was chosen to be disjoint from the root hyperplane r 0 induces an embedding  $r_0'\colon \mathbb P^{d-1} \hookrightarrow T'$, which we take to be the new root hyperplane. Repeat finitely many times.
$r_0'\colon \mathbb P^{d-1} \hookrightarrow T'$, which we take to be the new root hyperplane. Repeat finitely many times.
An n-pointed rooted tree is such a rooted tree of projective spaces ![]() $T$ together with n distinct points
$T$ together with n distinct points
lying outside the singular locus ![]() $\text{Sing}(T)$ and outside the root hyperplane.
$\text{Sing}(T)$ and outside the root hyperplane.
Remark. When d = 1, blowing up in a smooth point does nothing and hyperplanes are points so an n-pointed rooted tree of 1-dimensional projective spaces is just an n + 1-pointed genus 0 curve with at worst nodal singularities.
Decompose ![]() $T=\bigcup_i T_i$ into irreducible components and let
$T=\bigcup_i T_i$ into irreducible components and let ![]() $T_0$ denote the root component, i.e. the component containing the root hyperplane. Each
$T_0$ denote the root component, i.e. the component containing the root hyperplane. Each ![]() $T_i$ is isomorphic to
$T_i$ is isomorphic to ![]() $\mathbb{P}^d$ blown up at a closed subscheme Qi consisting of finitely many disjoint
$\mathbb{P}^d$ blown up at a closed subscheme Qi consisting of finitely many disjoint ![]() $\mathbb{k}$-points, hence admits a canonical blow-down map
$\mathbb{k}$-points, hence admits a canonical blow-down map
Furthermore, there is an embedding ![]() $r_i\colon \mathbb P^{d-1}\hookrightarrow T_i$ for each Ti such that
$r_i\colon \mathbb P^{d-1}\hookrightarrow T_i$ for each Ti such that ![]() $b_i\circ r_i\colon \mathbb P^{d-1} \to \mathbb P^d$ is the inclusion of a hyperplane. For the root component r 0 is the root hyperplane and for other components
$b_i\circ r_i\colon \mathbb P^{d-1} \to \mathbb P^d$ is the inclusion of a hyperplane. For the root component r 0 is the root hyperplane and for other components ![]() $r_i$ is the embedding of the hyperplane along which the component was attached. Note that the disjoint union of
$r_i$ is the embedding of the hyperplane along which the component was attached. Note that the disjoint union of ![]() $r_i$ and the exceptional divisor
$r_i$ and the exceptional divisor ![]() $E_i$ of the blow-up
$E_i$ of the blow-up ![]() $T_i \to \mathbb P^d$ is precisely the intersection
$T_i \to \mathbb P^d$ is precisely the intersection ![]() $T_i\cap~\text{Sing}(T)$.
$T_i\cap~\text{Sing}(T)$.
Definition 4.5. With notation as above, the n-pointed rooted tree ![]() $T$ is stable if, for every component
$T$ is stable if, for every component ![]() $T_i$, there are at least two corresponding special points, meaning the marked points
$T_i$, there are at least two corresponding special points, meaning the marked points ![]() $\{p_1,\dots, p_n\}\cap T_i$ and the blown-up points Qi.
$\{p_1,\dots, p_n\}\cap T_i$ and the blown-up points Qi.
Remark. This condition is equivalent to ![]() $T$ having no non-trivial automorphisms restricting to the identity on the marked points and the root hyperplane.
$T$ having no non-trivial automorphisms restricting to the identity on the marked points and the root hyperplane.
Remark. When d = 1, the above condition is equivalent to there being three special points on each component if we think of the corresponding hyperplanes as special points as well. This is the usual stability condition for pointed genus 0 curves with at worst nodal singularities.
By theorem 3.4.4. in [Reference Chen, Gibney and Krashen5] the smooth varieties ![]() $T_{d,n}$ are moduli spaces of stable n-pointed rooted trees of d-dimensional projective spaces. There are no stable 1-pointed trees but in this case we define
$T_{d,n}$ are moduli spaces of stable n-pointed rooted trees of d-dimensional projective spaces. There are no stable 1-pointed trees but in this case we define ![]() $T_{d,1}=~\text{Spec } \mathbb{k}$. As mentioned before, a hyperplane in
$T_{d,1}=~\text{Spec } \mathbb{k}$. As mentioned before, a hyperplane in ![]() $\mathbb P^1$ is just a point and thus we have
$\mathbb P^1$ is just a point and thus we have ![]() $T_{1,n} \cong \overline{M}_{0,n+1}$, the moduli space of stable n + 1-pointed rational curves where the additional point is the root hyperplane.
$T_{1,n} \cong \overline{M}_{0,n+1}$, the moduli space of stable n + 1-pointed rational curves where the additional point is the root hyperplane.
Each variety ![]() $T_{d,n}$ comes with a canonical action by the symmetric group
$T_{d,n}$ comes with a canonical action by the symmetric group ![]() $\Sigma_n$ corresponding to permutation of the marked points. Furthermore, for each
$\Sigma_n$ corresponding to permutation of the marked points. Furthermore, for each ![]() $1\leq i \leq n$ there is a morphism
$1\leq i \leq n$ there is a morphism
 \begin{equation*}T_{d,n}\times T_{d,m}\xrightarrow{\circ_i} T_{d,n+m-1}\end{equation*}
\begin{equation*}T_{d,n}\times T_{d,m}\xrightarrow{\circ_i} T_{d,n+m-1}\end{equation*} which takes an n-pointed tree ![]() $T$ and an m-pointed tree
$T$ and an m-pointed tree ![]() $T$ʹ and maps them to the
$T$ʹ and maps them to the ![]() $n+m-1$ pointed tree formed by blowing-up
$n+m-1$ pointed tree formed by blowing-up ![]() $T$ in the ith marked point and gluing the resulting exceptional divisor to the root hyperplane in
$T$ in the ith marked point and gluing the resulting exceptional divisor to the root hyperplane in ![]() $T$ʹ. It is clear from definitions that these maps give rise to an operad of varieties, which we denote
$T$ʹ. It is clear from definitions that these maps give rise to an operad of varieties, which we denote ![]() $\text{\textbf{CGK}}_d$, with spaces
$\text{\textbf{CGK}}_d$, with spaces ![]() $\text{\textbf{CGK}}_d(n) = T_{d,n}$. In the case d = 1 this construction is classical, see for example [Reference Getzler and Kapranov11].
$\text{\textbf{CGK}}_d(n) = T_{d,n}$. In the case d = 1 this construction is classical, see for example [Reference Getzler and Kapranov11].
4.3. Definition and properties of  $T_{d,n}$
$T_{d,n}$
In this section we recall the definition and some important properties of the ![]() $T_{d,n}$ spaces from [Reference Chen, Gibney and Krashen5]. We also introduce a functor of points for these spaces and use this to define the operad
$T_{d,n}$ spaces from [Reference Chen, Gibney and Krashen5]. We also introduce a functor of points for these spaces and use this to define the operad ![]() $\text{\textbf{CGK}}_d$ with spaces
$\text{\textbf{CGK}}_d$ with spaces ![]() $\text{\textbf{CGK}}_d(n) = T_{d,n}$ which was informally described in section 4.2. We will not explicitly prove that
$\text{\textbf{CGK}}_d(n) = T_{d,n}$ which was informally described in section 4.2. We will not explicitly prove that ![]() $\text{\textbf{CGK}}_d$ is isomorphic to the operad described in section 4.2 but it is not hard to show using theorem 3.4.4. in [Reference Chen, Gibney and Krashen5].
$\text{\textbf{CGK}}_d$ is isomorphic to the operad described in section 4.2 but it is not hard to show using theorem 3.4.4. in [Reference Chen, Gibney and Krashen5].
If ![]() $\text{pr}_i\colon X^n \to X$ denotes the projection to the ith component it is clear from definitions that the composition
$\text{pr}_i\colon X^n \to X$ denotes the projection to the ith component it is clear from definitions that the composition
 \begin{equation*}D([n])\hookrightarrow~\text{FM}^{\text{alg}}_n(X) \xrightarrow{\rho} X^n \xrightarrow{\text{pr}_i} X\end{equation*}
\begin{equation*}D([n])\hookrightarrow~\text{FM}^{\text{alg}}_n(X) \xrightarrow{\rho} X^n \xrightarrow{\text{pr}_i} X\end{equation*} is independent of the integer i. We denote this morphism by ![]() $\pi \colon D([n]) \to X$. In [Reference Chen, Gibney and Krashen5], Chen, Gibney, and Krashen show that for any
$\pi \colon D([n]) \to X$. In [Reference Chen, Gibney and Krashen5], Chen, Gibney, and Krashen show that for any ![]() $\mathbb{k}$-valued point
$\mathbb{k}$-valued point ![]() $x\in X$ the fibre
$x\in X$ the fibre ![]() $\pi^{-1}(x)$, depends only on n and
$\pi^{-1}(x)$, depends only on n and ![]() $\dim X$ up to (non-canonical) isomorphism provided that X is smooth. We define
$\dim X$ up to (non-canonical) isomorphism provided that X is smooth. We define ![]() $T_{d,n}$ as
$T_{d,n}$ as ![]() $\pi^{-1}(0)$ for the map
$\pi^{-1}(0)$ for the map ![]() $\pi\colon D([n]) \to \mathbb A^d$ but by the above we could equally well have taken any other smooth variety instead of
$\pi\colon D([n]) \to \mathbb A^d$ but by the above we could equally well have taken any other smooth variety instead of ![]() $X= \mathbb A^d$.
$X= \mathbb A^d$.
Remark. Just like the topological case notice that while we have up until this point indexed coordinates with ![]() $[n]$ we are free to use any finite index set
$[n]$ we are free to use any finite index set ![]() $I$ and
$I$ and  $\text{FM}^{\text{alg}}_I(X)$ and
$\text{FM}^{\text{alg}}_I(X)$ and ![]() $T_{d,I}$ together with all related maps and divisors are defined in the analogous way.
$T_{d,I}$ together with all related maps and divisors are defined in the analogous way.
The variety ![]() $T_{d,n}$ is smooth and comes equipped with a smooth closed subscheme
$T_{d,n}$ is smooth and comes equipped with a smooth closed subscheme ![]() $T_{d,n}(I)$ for every non empty
$T_{d,n}(I)$ for every non empty ![]() $I \subseteq [n]$. For
$I \subseteq [n]$. For ![]() $I \in P_2({n})$, i.e.
$I \in P_2({n})$, i.e. ![]() $I\neq [n]$ and
$I\neq [n]$ and ![]() $\vert I \vert\geq 2$, we define
$\vert I \vert\geq 2$, we define ![]() $T_{d,n}(I)$ as the pullback of
$T_{d,n}(I)$ as the pullback of ![]() $D(I)\subseteq~\text{FM}^{\text{alg}}_n(X)$ to
$D(I)\subseteq~\text{FM}^{\text{alg}}_n(X)$ to ![]() $T_{d,n}$. For other
$T_{d,n}$. For other ![]() $I$ (i.e.
$I$ (i.e. ![]() $I$ is
$I$ is ![]() $[n]$ or a one point set) we take
$[n]$ or a one point set) we take ![]() $T_{d,n}(I) := T_{d,n}$. Similarly, for a collection of (distinct) subsets
$T_{d,n}(I) := T_{d,n}$. Similarly, for a collection of (distinct) subsets ![]() $I_1,\dots, I_k \subseteq [n]$ we define
$I_1,\dots, I_k \subseteq [n]$ we define ![]() $T_{d,n}(I_1,\dots, I_k) := \bigcap_{i}T_{d,n}(I_i)$. For
$T_{d,n}(I_1,\dots, I_k) := \bigcap_{i}T_{d,n}(I_i)$. For ![]() $I\neq [n]$ and
$I\neq [n]$ and ![]() $\vert I \vert\geq 2$ the subscheme
$\vert I \vert\geq 2$ the subscheme ![]() $T_{d,n}(I)$ is a smooth divisor of
$T_{d,n}(I)$ is a smooth divisor of ![]() $T_{d,n}$ and the union of all these divisors is a normal crossings divisor. Additionally, the intersection
$T_{d,n}$ and the union of all these divisors is a normal crossings divisor. Additionally, the intersection ![]() $T_{d,n}(I_1,\dots, I_k)$ is non empty if and only if
$T_{d,n}(I_1,\dots, I_k)$ is non empty if and only if ![]() $(I_1,\dots, I_k)$ is nested. All this essentially follows from the analogous results for
$(I_1,\dots, I_k)$ is nested. All this essentially follows from the analogous results for ![]() $\text{FM}^{\text{alg}}_n(X)$ recalled in section 4.1. Details can be found in [Reference Chen, Gibney and Krashen5].
$\text{FM}^{\text{alg}}_n(X)$ recalled in section 4.1. Details can be found in [Reference Chen, Gibney and Krashen5].
Remark. In terms of pointed trees ![]() $T_{d,n}(I)$, where
$T_{d,n}(I)$, where ![]() $I\in P_2({[n]})$, parameterizes trees which have two (not necessarily irreducible) components such that the component which does not contain the root hyperplane contains exactly those marked points indexed by
$I\in P_2({[n]})$, parameterizes trees which have two (not necessarily irreducible) components such that the component which does not contain the root hyperplane contains exactly those marked points indexed by ![]() $I$.
$I$.
The first goal of this section will be to give a functor of points description of the schemes ![]() $T_{d,n}(I_1,\dots, I_k)$. For this we introduce the following.
$T_{d,n}(I_1,\dots, I_k)$. For this we introduce the following.
Definition 4.6. For a scheme ![]() $H$, an integer d, and a finite, non-empty, set
$H$, an integer d, and a finite, non-empty, set ![]() $I$ with at least two element we let
$I$ with at least two element we let  $\mathcal F^{H,d}_I$ denote the quasi-coherent sheaf of modules defined by
$\mathcal F^{H,d}_I$ denote the quasi-coherent sheaf of modules defined by
 \begin{equation*}\mathcal F^{H,d}_I := \left\langle \{t_{ij}^k\}_{i,j \in I}^{1\leq k\leq d}\right \rangle \Bigm / \sim.\end{equation*}
\begin{equation*}\mathcal F^{H,d}_I := \left\langle \{t_{ij}^k\}_{i,j \in I}^{1\leq k\leq d}\right \rangle \Bigm / \sim.\end{equation*} Here  $\left\langle \{t_{ij}^k\}_{i,j \in I}^{1\leq k\leq d}\right \rangle$ denotes the free module with generators
$\left\langle \{t_{ij}^k\}_{i,j \in I}^{1\leq k\leq d}\right \rangle$ denotes the free module with generators ![]() $t_{ij}^k$ and ∼ is generated by sections of the form
$t_{ij}^k$ and ∼ is generated by sections of the form  $t_{ij}^k +t_{jl}^k-t_{il}^k$. We will also denote this by
$t_{ij}^k +t_{jl}^k-t_{il}^k$. We will also denote this by ![]() $\mathcal F_I^d$ or
$\mathcal F_I^d$ or ![]() $\mathcal F_I$ if H or
$\mathcal F_I$ if H or ![]() $H,d$ are clear from context.
$H,d$ are clear from context.
For every function of sets ![]() $\varphi\colon I\to J$ we let
$\varphi\colon I\to J$ we let  $F_{\varphi}\colon \mathcal F_{I}^{H,d} \hookrightarrow \mathcal F_J^{H,d}$ denote the sheaf morphism defined by sending
$F_{\varphi}\colon \mathcal F_{I}^{H,d} \hookrightarrow \mathcal F_J^{H,d}$ denote the sheaf morphism defined by sending  $t_{ij}^k \mapsto t_{\varphi(i)\varphi(j)}^k.$
$t_{ij}^k \mapsto t_{\varphi(i)\varphi(j)}^k.$
Remark. Note that  $\mathcal F^{H,d}_I$ is free of rank
$\mathcal F^{H,d}_I$ is free of rank ![]() $d(\vert I \vert-1)$. Furthermore, note that the sheaves
$d(\vert I \vert-1)$. Furthermore, note that the sheaves  $\mathcal F^{H,d}_I$ and the maps
$\mathcal F^{H,d}_I$ and the maps ![]() $F_{\varphi}$ are pullbacks of corresponding vector bundles with morphisms on
$F_{\varphi}$ are pullbacks of corresponding vector bundles with morphisms on ![]() $\text{Spec } \mathbb{k}$. For all
$\text{Spec } \mathbb{k}$. For all ![]() $I \in P_2({n})$ these are in turn isomorphic to the pullbacks of the ideal sheaves
$I \in P_2({n})$ these are in turn isomorphic to the pullbacks of the ideal sheaves ![]() $\mathcal I_{\Delta_I}$ on
$\mathcal I_{\Delta_I}$ on  $(\mathbb A^d)^n \cong~\text{Spec } \mathbb{k}[x^k_i]_{1\leq i \leq n}^{1\leq k \leq d}$ via the inclusion of the origin
$(\mathbb A^d)^n \cong~\text{Spec } \mathbb{k}[x^k_i]_{1\leq i \leq n}^{1\leq k \leq d}$ via the inclusion of the origin ![]() $\text{Spec } \mathbb{k} \hookrightarrow (\mathbb A^d)^n$. Here we identify the section
$\text{Spec } \mathbb{k} \hookrightarrow (\mathbb A^d)^n$. Here we identify the section ![]() $t_{ij}^k$ of
$t_{ij}^k$ of ![]() $\mathcal F^{d}_I$ with the pullback of the global section
$\mathcal F^{d}_I$ with the pullback of the global section  $x_i^k-x^k_j \in I_{\Delta_I} \subseteq \mathbb{k}[x^k_i]$. Additionally, if
$x_i^k-x^k_j \in I_{\Delta_I} \subseteq \mathbb{k}[x^k_i]$. Additionally, if ![]() $I\subseteq J \subseteq [n]$ the map
$I\subseteq J \subseteq [n]$ the map ![]() $F_{I\hookrightarrow J}$ of sheaves on
$F_{I\hookrightarrow J}$ of sheaves on ![]() $\text{Spec } \mathbb{k}$ is the pullback of the ideal inclusion map
$\text{Spec } \mathbb{k}$ is the pullback of the ideal inclusion map ![]() $\mathcal I_{\Delta_I} \hookrightarrow \mathcal I_{\Delta_J}$.
$\mathcal I_{\Delta_I} \hookrightarrow \mathcal I_{\Delta_J}$.
Definition 4.7. Let ![]() $\mathcal T_{d,n}\colon Sch^{op}\to Set$ be the functor which sends
$\mathcal T_{d,n}\colon Sch^{op}\to Set$ be the functor which sends ![]() $H$ to the set of collections of invertible quotients,
$H$ to the set of collections of invertible quotients,
 \begin{equation*} \{\phi_I\colon \mathcal F^{H,d}_I \twoheadrightarrow \mathcal L_I\} _{I \in P_2({n})},\end{equation*}
\begin{equation*} \{\phi_I\colon \mathcal F^{H,d}_I \twoheadrightarrow \mathcal L_I\} _{I \in P_2({n})},\end{equation*} such that for every ![]() $I \subseteq J$ there is a morphism
$I \subseteq J$ there is a morphism ![]() $\mathcal L_I \to \mathcal L_J$ making the following diagram commute.
$\mathcal L_I \to \mathcal L_J$ making the following diagram commute.

Such a collection will sometimes be referred to as a simple screen. Similarly let ![]() $\mathcal T_{d,n}(I_1,\dots, I_k)$ denote the subfunctor of
$\mathcal T_{d,n}(I_1,\dots, I_k)$ denote the subfunctor of ![]() $\mathcal T_{d,n}$ with the added condition that for every
$\mathcal T_{d,n}$ with the added condition that for every ![]() $I_r$, the simple screens satisfy the
$I_r$, the simple screens satisfy the ![]() $I_r$-vanishing property, i.e. if
$I_r$-vanishing property, i.e. if ![]() $J\nsubseteq I_r$ and
$J\nsubseteq I_r$ and ![]() $\vert J\cap I_r\vert \geq 2$ then
$\vert J\cap I_r\vert \geq 2$ then ![]() $\mathcal L_{J\cap I_r} \to \mathcal L_J$ is the zero morphism.
$\mathcal L_{J\cap I_r} \to \mathcal L_J$ is the zero morphism.
Remark. Note that ![]() $\mathcal T_{d,n}([n]) = \mathcal T_{d,n}( \{i\} ) = \mathcal T_{d,n}$.
$\mathcal T_{d,n}([n]) = \mathcal T_{d,n}( \{i\} ) = \mathcal T_{d,n}$.
There is a natural simple screen on ![]() $T_{d,n}$ which can be constructed as follows. Let
$T_{d,n}$ which can be constructed as follows. Let  $i\colon T_{d,n}\hookrightarrow~\text{FM}^{\text{alg}}_n(\mathbb A^d)$ denote the inclusion of the fibre over the origin in
$i\colon T_{d,n}\hookrightarrow~\text{FM}^{\text{alg}}_n(\mathbb A^d)$ denote the inclusion of the fibre over the origin in ![]() $(\mathbb A^d)^n$. The ideal sheaves
$(\mathbb A^d)^n$. The ideal sheaves ![]() $\mathcal I_I$ pull back to
$\mathcal I_I$ pull back to ![]() $i^* \mathcal I_I \cong \mathcal F_I^d$ and for
$i^* \mathcal I_I \cong \mathcal F_I^d$ and for ![]() $I\subseteq J$ the inclusion
$I\subseteq J$ the inclusion ![]() $\mathcal I_I \hookrightarrow \mathcal I_J$ pulls back to the map
$\mathcal I_I \hookrightarrow \mathcal I_J$ pulls back to the map ![]() $F_{I\subseteq J}\colon \mathcal F_I^d\to \mathcal F_J^d$. Thus, the universal screen on
$F_{I\subseteq J}\colon \mathcal F_I^d\to \mathcal F_J^d$. Thus, the universal screen on  $\text{FM}^{\text{alg}}_n(\mathbb A^d)$ pulls back to a simple screen on
$\text{FM}^{\text{alg}}_n(\mathbb A^d)$ pulls back to a simple screen on ![]() $T_{d,n}$ via i. We will refer to this as the universal simple screen on
$T_{d,n}$ via i. We will refer to this as the universal simple screen on ![]() $T_{d,n}$. Let
$T_{d,n}$. Let  $\mathcal F_I\twoheadrightarrow \mathcal M_I^{d,n}$ denote the invertible quotient corresponding to
$\mathcal F_I\twoheadrightarrow \mathcal M_I^{d,n}$ denote the invertible quotient corresponding to ![]() $I \in P_2({n})$ of the universal simple screen on
$I \in P_2({n})$ of the universal simple screen on ![]() $T_{d,n}$. We will also denote this by
$T_{d,n}$. We will also denote this by ![]() $\mathcal M_I$ if
$\mathcal M_I$ if ![]() $d,n$ are clear from context.
$d,n$ are clear from context.
Lemma 4.8. Let  $i\colon T_{d,n} \to~\text{FM}^{\text{alg}}_n(\mathbb A^d)$ denote the inclusion of the fibre over the origin. There are unique isomorphisms
$i\colon T_{d,n} \to~\text{FM}^{\text{alg}}_n(\mathbb A^d)$ denote the inclusion of the fibre over the origin. There are unique isomorphisms
 \begin{equation*}\bigotimes_{I \subseteq I'} i^* \mathcal O(-D(I')) \xrightarrow{\cong} \mathcal M_I\end{equation*}
\begin{equation*}\bigotimes_{I \subseteq I'} i^* \mathcal O(-D(I')) \xrightarrow{\cong} \mathcal M_I\end{equation*} such that for ![]() $I \subseteq R$ the following diagram commutes
$I \subseteq R$ the following diagram commutes

where ![]() $t_{R'}\colon O(-D(R')) \hookrightarrow \mathcal O$ denotes the ideal inclusion.
$t_{R'}\colon O(-D(R')) \hookrightarrow \mathcal O$ denotes the ideal inclusion.
Proof. This follows from the analogous result for the universal screen on ![]() $\text{FM}^{\text{alg}}_n(X)$.
$\text{FM}^{\text{alg}}_n(X)$.
Proposition 4.9. The functor ![]() $\mathcal T_{d,n}$ is represented by
$\mathcal T_{d,n}$ is represented by ![]() $T_{d,n}$ and similarly
$T_{d,n}$ and similarly ![]() $\mathcal T_{d,n}(I_1,\dots, I_k)$ is represented by
$\mathcal T_{d,n}(I_1,\dots, I_k)$ is represented by ![]() $T_{d,n}(I_1,\dots, I_k)$. Furthermore, the natural isomorphism
$T_{d,n}(I_1,\dots, I_k)$. Furthermore, the natural isomorphism ![]() $\hom(-,T_{d,n}) \to \mathcal T_{d,n}$ is given by sending a map
$\hom(-,T_{d,n}) \to \mathcal T_{d,n}$ is given by sending a map ![]() $f\colon H \to T_{d,n}$ to the pullback of the universal simple screen on
$f\colon H \to T_{d,n}$ to the pullback of the universal simple screen on ![]() $T_{d,n}$ to
$T_{d,n}$ to ![]() $H$. The analogous result holds for
$H$. The analogous result holds for ![]() $\hom(-,T_{d,n}(I_1,\dots,I_k)) \to \mathcal T_{d,n}(I_1,\dots,I_k)$.
$\hom(-,T_{d,n}(I_1,\dots,I_k)) \to \mathcal T_{d,n}(I_1,\dots,I_k)$.
Proof. First note that if ![]() $i_0\colon~\text{Spec } \mathbb{k} \to (\mathbb A^d)^n$ denotes the inclusion of the origin then we have seen that
$i_0\colon~\text{Spec } \mathbb{k} \to (\mathbb A^d)^n$ denotes the inclusion of the origin then we have seen that ![]() $i_0^*\mathcal I_I = \mathcal F_I$ for every
$i_0^*\mathcal I_I = \mathcal F_I$ for every ![]() $I \in P_2({n})$, where
$I \in P_2({n})$, where ![]() $\mathcal I_I$ is the ideal sheaf corresponding to the I-diagonal in
$\mathcal I_I$ is the ideal sheaf corresponding to the I-diagonal in ![]() $(\mathbb A^d)^n$. Since
$(\mathbb A^d)^n$. Since
 \begin{equation*}T_{d,n} = \pi^{-1}(0) = D([n])\times_{\mathbb A^d}~\text{Spec } \mathbb{k} \cong D([n])\times_{(\mathbb A^d)^n}~\text{Spec } \mathbb{k}\end{equation*}
\begin{equation*}T_{d,n} = \pi^{-1}(0) = D([n])\times_{\mathbb A^d}~\text{Spec } \mathbb{k} \cong D([n])\times_{(\mathbb A^d)^n}~\text{Spec } \mathbb{k}\end{equation*} the result follows immediately from proposition 4.3. The same argument also gives the ![]() $T_{d,n}(I_1,\dots, I_k)$ case.
$T_{d,n}(I_1,\dots, I_k)$ case.
This functorial description simplifies the proof of many of the following results greatly. Let n be a positive integer, and let ![]() $q\colon [n]\twoheadrightarrow M$ be a surjection of sets. We also let q to denote the restriction of this map
$q\colon [n]\twoheadrightarrow M$ be a surjection of sets. We also let q to denote the restriction of this map ![]() $J \to q(J)$ for any
$J \to q(J)$ for any ![]() $J\subseteq M$.
$J\subseteq M$.
Proposition 4.10. The composition map described in section 4.2 is well defined and gives an isomorphism
 \begin{equation*}T_{d,n}\times \prod_{r=1}^n T_{d,q^{-1}(r)} \cong T_{d,M}(q^{-1}(1),\dots, q^{-1}(n)).\end{equation*}
\begin{equation*}T_{d,n}\times \prod_{r=1}^n T_{d,q^{-1}(r)} \cong T_{d,M}(q^{-1}(1),\dots, q^{-1}(n)).\end{equation*}Proof. We will construct an explicit natural isomorphism between the functors represented by the left and the right side. Identifying the induced isomorphism of schemes with the map described in section 4.2 is left as an unimportant exercise for the reader.
We define this natural transformation
 \begin{equation*}\mathcal T_{d,n}\times \prod_{r=1}^n \mathcal T_{d,q^{-1}(r)}\to \mathcal T_{d,M}(q^{-1}(1),\dots,q^{-1}(n))\end{equation*}
\begin{equation*}\mathcal T_{d,n}\times \prod_{r=1}^n \mathcal T_{d,q^{-1}(r)}\to \mathcal T_{d,M}(q^{-1}(1),\dots,q^{-1}(n))\end{equation*} by sending simple screens (on some ![]() $\mathbb{k}$-scheme
$\mathbb{k}$-scheme ![]() $H$)
$H$)
 \begin{equation*} \{\phi_I\colon \mathcal F_{I}\!\to\! \mathcal L^0_I\} _{I\in P_2({n})} \times \prod_{r=1}^{n} \{\psi^r_{J}\colon \mathcal F_{J}\!\to\! \mathcal L^r_{J}\} _{J\in P_2({q^{-1}(r)})} \!\to\! \{\rho_K\colon \mathcal F_K\to \mathcal L_K\} _{K\in P_2({M})},\end{equation*}
\begin{equation*} \{\phi_I\colon \mathcal F_{I}\!\to\! \mathcal L^0_I\} _{I\in P_2({n})} \times \prod_{r=1}^{n} \{\psi^r_{J}\colon \mathcal F_{J}\!\to\! \mathcal L^r_{J}\} _{J\in P_2({q^{-1}(r)})} \!\to\! \{\rho_K\colon \mathcal F_K\to \mathcal L_K\} _{K\in P_2({M})},\end{equation*} where ![]() $ \{\rho_K\colon \mathcal F_K\to \mathcal L_K\} _{K\in P_2({M})}$ is defined as follows. We define the line bundles
$ \{\rho_K\colon \mathcal F_K\to \mathcal L_K\} _{K\in P_2({M})}$ is defined as follows. We define the line bundles ![]() $\mathcal L_K$ as
$\mathcal L_K$ as
 \begin{equation*}\mathcal L_K = \begin{cases}
\mathcal L^r_{K} & K \subseteq q^{-1}(r)~\text{some } r\\
\mathcal L^0_{q(K)}&~\text{else}
\end{cases}\end{equation*}
\begin{equation*}\mathcal L_K = \begin{cases}
\mathcal L^r_{K} & K \subseteq q^{-1}(r)~\text{some } r\\
\mathcal L^0_{q(K)}&~\text{else}
\end{cases}\end{equation*}and the corresponding quotients as
 \begin{equation*}\rho_K = \begin{cases}
\psi^r_{K} & K \subseteq q^{-1}(r),~\text{some } r\\
\phi_{q(K)} \circ F_{q} &~\text{else}
\end{cases}.\end{equation*}
\begin{equation*}\rho_K = \begin{cases}
\psi^r_{K} & K \subseteq q^{-1}(r),~\text{some } r\\
\phi_{q(K)} \circ F_{q} &~\text{else}
\end{cases}.\end{equation*} For the definition of ![]() $F_q\colon \mathcal F_{K}\to \mathcal F_{q(K)}$, see definition 4.6. We define the maps
$F_q\colon \mathcal F_{K}\to \mathcal F_{q(K)}$, see definition 4.6. We define the maps ![]() $\mathcal L_{K_1} \to \mathcal L_{K_2}$, for
$\mathcal L_{K_1} \to \mathcal L_{K_2}$, for ![]() $K_1 \subseteq K_2$, to be
$K_1 \subseteq K_2$, to be
 \begin{equation*}\begin{cases}
\mathcal L^r_{K_1} \to \mathcal L^r_{K_2} & K_2 \subseteq q^{-1}(r)~\text{some } r\\
\mathcal L^0_{q(K_1)} \to \mathcal L^0_{q (K_2)} & K_1 \not\subseteq q^{-1}(r)~\text{any } r\\
0 & K_1 \subseteq q^{-1}(r)~\text{and } K_2 \not \subseteq q^{-1}(r)
\end{cases}.\end{equation*}
\begin{equation*}\begin{cases}
\mathcal L^r_{K_1} \to \mathcal L^r_{K_2} & K_2 \subseteq q^{-1}(r)~\text{some } r\\
\mathcal L^0_{q(K_1)} \to \mathcal L^0_{q (K_2)} & K_1 \not\subseteq q^{-1}(r)~\text{any } r\\
0 & K_1 \subseteq q^{-1}(r)~\text{and } K_2 \not \subseteq q^{-1}(r)
\end{cases}.\end{equation*} It is easy to check that ![]() $ \{\rho_K\} _{K\in P_2({M})}$ with the maps
$ \{\rho_K\} _{K\in P_2({M})}$ with the maps ![]() $\mathcal L_{K_1} \to \mathcal L_{K_2}$ above is a simple screen with the
$\mathcal L_{K_1} \to \mathcal L_{K_2}$ above is a simple screen with the ![]() $q^{-1}(r)$-vanishing property for every
$q^{-1}(r)$-vanishing property for every ![]() $r$ and so this transformation is well defined on the level of sets. Furthermore, the map is clearly natural and so we have defined a natural transformation as desired.
$r$ and so this transformation is well defined on the level of sets. Furthermore, the map is clearly natural and so we have defined a natural transformation as desired.
To show that this gives a natural isomorphism first note that that this map is clearly injective. Surjectivity follows from the fact that if ![]() $ \{\rho_K\colon \mathcal F_K\to \mathcal L_K\} _{K\in P_2({M})}$ is a simple screen satisfying the
$ \{\rho_K\colon \mathcal F_K\to \mathcal L_K\} _{K\in P_2({M})}$ is a simple screen satisfying the ![]() $q^{-1}(r)$-vanishing property for every r then, for every K not contained in any
$q^{-1}(r)$-vanishing property for every r then, for every K not contained in any ![]() $q^{-1}(r)$ the map
$q^{-1}(r)$ the map ![]() $\rho_K\colon \mathcal F_K\to \mathcal L_K$ factorizes uniquely as
$\rho_K\colon \mathcal F_K\to \mathcal L_K$ factorizes uniquely as

by the universal property of the quotient.
Remark. Since we defined ![]() $T_{d,n}( \{i\} ) = T_{d,n}([n]) = T_{d,n}$ this statement is true even in the case n = 1 or
$T_{d,n}( \{i\} ) = T_{d,n}([n]) = T_{d,n}$ this statement is true even in the case n = 1 or ![]() $\vert q^{-1}(r) \vert =1$.
$\vert q^{-1}(r) \vert =1$.
Corollary 4.11. For any ![]() $I \in P_2({n})$, the isomorphism of the proposition restricts to an isomorphism of closed subvarieties
$I \in P_2({n})$, the isomorphism of the proposition restricts to an isomorphism of closed subvarieties
 \begin{equation*}T_{d,n}(I)\times \prod_{r=1}^nT_{d,q^{-1}(r)}\cong T_{d,M}(q^{-1}(1), \dots, q^{-1}(n), q^{-1}(I)).\end{equation*}
\begin{equation*}T_{d,n}(I)\times \prod_{r=1}^nT_{d,q^{-1}(r)}\cong T_{d,M}(q^{-1}(1), \dots, q^{-1}(n), q^{-1}(I)).\end{equation*} Similarly, for any ![]() $I_r\in P_2({q^{-1}(r)})$, the isomorphism of the proposition restricts to an isomorphism of closed subschemes
$I_r\in P_2({q^{-1}(r)})$, the isomorphism of the proposition restricts to an isomorphism of closed subschemes
 \begin{equation*}T_{d,n}\times T_{d,q^{-1}(1)}\times\dots\times T_{d,q^{-1}(r)}(I_r)\times \dots\times T_{d,q^{-1}(n)} \cong T_{d,M}(q^{-1}(1), \dots, q^{-1}(n), I_r).\end{equation*}
\begin{equation*}T_{d,n}\times T_{d,q^{-1}(1)}\times\dots\times T_{d,q^{-1}(r)}(I_r)\times \dots\times T_{d,q^{-1}(n)} \cong T_{d,M}(q^{-1}(1), \dots, q^{-1}(n), I_r).\end{equation*}Proof. The proof is analogous.
Corollary 4.12. Let ![]() $\gamma\colon T_{d,n} \times \prod_{i=1}^n T_{d,q^{-1}(i)} \to T_{d,M}$ be the composition of the isomorphism above with the inclusion into
$\gamma\colon T_{d,n} \times \prod_{i=1}^n T_{d,q^{-1}(i)} \to T_{d,M}$ be the composition of the isomorphism above with the inclusion into ![]() $T_{d,M}$ and let
$T_{d,M}$ and let ![]() $\pi_0\colon T_{d,n} \times \prod_{i=1}^n T_{d,q^{-1}(i)} \to T_{d,n}$ and
$\pi_0\colon T_{d,n} \times \prod_{i=1}^n T_{d,q^{-1}(i)} \to T_{d,n}$ and ![]() $\pi_r \colon T_{d,n} \times \prod_{i=1}^n T_{d,q^{-1}(i)} \to T_{d,q^{-1}(r)}$ denote the corresponding projections. There are unique isomorphisms relating the elements of the corresponding universal screens
$\pi_r \colon T_{d,n} \times \prod_{i=1}^n T_{d,q^{-1}(i)} \to T_{d,q^{-1}(r)}$ denote the corresponding projections. There are unique isomorphisms relating the elements of the corresponding universal screens
 \begin{equation*}\gamma^*\mathcal M_I^{d,M} \xrightarrow{\cong} \begin{cases}
\pi_r^* \mathcal M^{d,q^{-1}(r)}_{I} & I \subseteq q^{-1}(r)~\text{some } r\\
\pi^*_0\mathcal M^{d,n}_{q(I)}&~\text{else}
\end{cases}.\end{equation*}
\begin{equation*}\gamma^*\mathcal M_I^{d,M} \xrightarrow{\cong} \begin{cases}
\pi_r^* \mathcal M^{d,q^{-1}(r)}_{I} & I \subseteq q^{-1}(r)~\text{some } r\\
\pi^*_0\mathcal M^{d,n}_{q(I)}&~\text{else}
\end{cases}.\end{equation*}making (one of) the following diagrams commute:

Proof. This follows immediately from the construction and the definition of the universal screen on ![]() $T_{d,n}$.
$T_{d,n}$.
The next relevant property of the ![]() $T_{d,n}$ spaces is that the
$T_{d,n}$ spaces is that the ![]() $\Sigma_n$ action informally described in section 4.2 is well defined. Indeed, this action is precisely the restriction to
$\Sigma_n$ action informally described in section 4.2 is well defined. Indeed, this action is precisely the restriction to ![]() $T_{d,n}$ of the
$T_{d,n}$ of the ![]() $\Sigma_n$ action on the Fulton–MacPherson compactification
$\Sigma_n$ action on the Fulton–MacPherson compactification  $\text{FM}^{\text{alg}}_n(\mathbb A^d)$. For each
$\text{FM}^{\text{alg}}_n(\mathbb A^d)$. For each ![]() $\sigma \in \Sigma_n$, it is easy to verify that this action corresponds to the action on
$\sigma \in \Sigma_n$, it is easy to verify that this action corresponds to the action on ![]() $\mathcal T_{d,n}$ given by
$\mathcal T_{d,n}$ given by
 \begin{equation*} \{\phi_I\colon \mathcal F_I \!\twoheadrightarrow\! \mathcal L_I\} _{I \in P_2({n})} \!\in\! \mathcal T_{d,n}(H) \mapsto \{\phi_{\sigma^{-1}(I)} \circ\sigma^{-1}_I \!\colon\! \mathcal F_I \!\twoheadrightarrow\! \mathcal L_{\sigma^{-1}(I)}\} _{I \in P_2({n})} \!\in\! \mathcal T_{d,n}(H),\end{equation*}
\begin{equation*} \{\phi_I\colon \mathcal F_I \!\twoheadrightarrow\! \mathcal L_I\} _{I \in P_2({n})} \!\in\! \mathcal T_{d,n}(H) \mapsto \{\phi_{\sigma^{-1}(I)} \circ\sigma^{-1}_I \!\colon\! \mathcal F_I \!\twoheadrightarrow\! \mathcal L_{\sigma^{-1}(I)}\} _{I \in P_2({n})} \!\in\! \mathcal T_{d,n}(H),\end{equation*}where
is defined by sending  $t_{ij}^k \mapsto t^k_{\sigma(i)\sigma(j)}$.
$t_{ij}^k \mapsto t^k_{\sigma(i)\sigma(j)}$.
With the maps we have constructed so far we can define the operad of schemes ![]() $\text{\textbf{CGK}}_d$ which was informally described in section 4.2. Its objects are
$\text{\textbf{CGK}}_d$ which was informally described in section 4.2. Its objects are ![]() $\text{\textbf{CGK}}_d(n) = T_{d,n}$, its composition maps are the morphisms of proposition 4.10 (composed with the inclusion
$\text{\textbf{CGK}}_d(n) = T_{d,n}$, its composition maps are the morphisms of proposition 4.10 (composed with the inclusion ![]() $T_{d,M}(q^{-1}(1),\dots, q^{-1}(n)) \hookrightarrow T_{d,M}$), and its symmetry action is the one described above. There is only one candidate for the unit morphism of the operad since
$T_{d,M}(q^{-1}(1),\dots, q^{-1}(n)) \hookrightarrow T_{d,M}$), and its symmetry action is the one described above. There is only one candidate for the unit morphism of the operad since ![]() $T_{d,1}\cong~\text{Spec } \mathbb{k}$. It is easy to, at least intuitively, see why these maps satisfy the operad axioms using their n-pointed rooted tree descriptions from section 4.2. Verifying that the axioms hold using the functorial descriptions of all relevant maps here is a more tedious, but easy, exercise.
$T_{d,1}\cong~\text{Spec } \mathbb{k}$. It is easy to, at least intuitively, see why these maps satisfy the operad axioms using their n-pointed rooted tree descriptions from section 4.2. Verifying that the axioms hold using the functorial descriptions of all relevant maps here is a more tedious, but easy, exercise.
Definition 4.13. The Chen, Gibney, Crashen operad, ![]() $\text{\textbf{CGK}}_d$ is the operad with objects
$\text{\textbf{CGK}}_d$ is the operad with objects ![]() $\text{\textbf{CGK}}_d(n) = T_{d,n}$ and with morphisms as described above.
$\text{\textbf{CGK}}_d(n) = T_{d,n}$ and with morphisms as described above.
Remark. This is an operad of smooth ![]() $\mathbb{k}$-varieties where all composition morphisms are closed embeddings and the unit map is the identity.
$\mathbb{k}$-varieties where all composition morphisms are closed embeddings and the unit map is the identity.
The case d = 1 here is of special interest. The operad ![]() $\text{\textbf{CGK}}_1$ is isomorphic to the “Deligne–Mumford”-operad whose objects are the moduli spaces of stable n + 1-pointed curves of genus 0,
$\text{\textbf{CGK}}_1$ is isomorphic to the “Deligne–Mumford”-operad whose objects are the moduli spaces of stable n + 1-pointed curves of genus 0, ![]() $\overline{\mathcal M}_{0,n+1}$. Indeed, as mentioned earlier, Chen, Gibney, and Krashen show that there are isomorphisms
$\overline{\mathcal M}_{0,n+1}$. Indeed, as mentioned earlier, Chen, Gibney, and Krashen show that there are isomorphisms ![]() $T_{1,n} \cong \overline{\mathcal M}_{0,n+1}$ and one can verify that these isomorphisms can be chosen such that they commute with the respective operad morphisms.
$T_{1,n} \cong \overline{\mathcal M}_{0,n+1}$ and one can verify that these isomorphisms can be chosen such that they commute with the respective operad morphisms.
5. Log geometric constructions
In this section we define log structures on the smooth varieties encountered in section 4 and extend the various morphisms to morphisms of log schemes. To this end the following lemma will be used repeatedly.
Lemma 5.1. Let ![]() $f\colon X\to Y$ be a map of schemes and let
$f\colon X\to Y$ be a map of schemes and let ![]() $D\subseteq X$,
$D\subseteq X$, ![]() $E\subseteq Y$ be effective Cartier divisors such that
$E\subseteq Y$ be effective Cartier divisors such that ![]() $f^{-1}(E) =D$ (scheme theoretically). Then there is a unique isomorphism
$f^{-1}(E) =D$ (scheme theoretically). Then there is a unique isomorphism
 \begin{equation*}f^*\mathcal O_Y(E) \xrightarrow{\cong} \mathcal O_X(D)\end{equation*}
\begin{equation*}f^*\mathcal O_Y(E) \xrightarrow{\cong} \mathcal O_X(D)\end{equation*} taking ![]() $f^*s_E \mapsto s_D$.
$f^*s_E \mapsto s_D$.
Proof. First note that since ![]() $f^{-1}(E) = D$ there is an epimorphism
$f^{-1}(E) = D$ there is an epimorphism ![]() $f^*\mathcal I_E \twoheadrightarrow \mathcal I_D$ commuting with the corresponding maps to
$f^*\mathcal I_E \twoheadrightarrow \mathcal I_D$ commuting with the corresponding maps to ![]() $\mathcal O_X$. Since
$\mathcal O_X$. Since ![]() $\mathcal I_E$ and
$\mathcal I_E$ and ![]() $ \mathcal I_D$ are ideal sheaves of divisors they are line bundles and since any quotient map of line bundles is an isomorphism this is an isomorphism. Taking duals now yields the result. Uniqueness is clear since an isomorphism of line bundles is uniquely determined by its value for a single generically non-zero section.
$ \mathcal I_D$ are ideal sheaves of divisors they are line bundles and since any quotient map of line bundles is an isomorphism this is an isomorphism. Taking duals now yields the result. Uniqueness is clear since an isomorphism of line bundles is uniquely determined by its value for a single generically non-zero section.
5.1. The log schemes  $\text{FM}^{\text{log}}_n(X)$,
$\text{FM}^{\text{log}}_n(X)$,  $\mathsf K_{d,n}$ and
$\mathsf K_{d,n}$ and  $\mathsf T_{d,n}$
$\mathsf T_{d,n}$
First, let us define the log geometric Fulton–MacPherson compactification which has the nice property that its analytification is the topological Fulton–MacPherson compactification of ![]() $\text{Conf} _n(\mathbb C^d)$,
$\text{Conf} _n(\mathbb C^d)$, ![]() $\text{FM}^\text{top}_n(\mathbb C^d)$.
$\text{FM}^\text{top}_n(\mathbb C^d)$.
Definition 5.2. For a smooth variety ![]() $X$, the log geometric Fulton–MacPherson compactification (of
$X$, the log geometric Fulton–MacPherson compactification (of ![]() $\text{Conf} _n(X)$), denoted
$\text{Conf} _n(X)$), denoted ![]() $\text{FM}^{\text{log}}_n(X)$, is the log variety with underlying scheme
$\text{FM}^{\text{log}}_n(X)$, is the log variety with underlying scheme ![]() $\text{FM}^{\text{alg}}_n(X)$ together with the line bundles with sections corresponding to the divisors
$\text{FM}^{\text{alg}}_n(X)$ together with the line bundles with sections corresponding to the divisors ![]() $D(I)$ for every
$D(I)$ for every ![]() $I \in P_2({n})$.
$I \in P_2({n})$.
Note that all of the line bundles with sections  $\mathcal O_{\text{FM}^{\text{alg}}_n(X)}(D(I))$ pull back to the trivial line bundle with a nowhere-vanishing section on
$\mathcal O_{\text{FM}^{\text{alg}}_n(X)}(D(I))$ pull back to the trivial line bundle with a nowhere-vanishing section on ![]() $\text{Conf} _n(X)$. This induces a morphism of log schemes
$\text{Conf} _n(X)$. This induces a morphism of log schemes ![]() $\text{Conf} _n(X) \to~\text{FM}^{\text{log}}_n(X)$. Furthermore, the following diagram commutes:
$\text{Conf} _n(X) \to~\text{FM}^{\text{log}}_n(X)$. Furthermore, the following diagram commutes:

Similarly, we can define a log geometric analog of ![]() $T_{d,n}$, denoted
$T_{d,n}$, denoted ![]() $\mathsf K_{d,n}$, by taking the underlying scheme to be
$\mathsf K_{d,n}$, by taking the underlying scheme to be ![]() $T_{d,n}$ and the log structure given by the pullback of this log structure on
$T_{d,n}$ and the log structure given by the pullback of this log structure on  $\text{FM}^{\text{alg}}_n(\mathbb A^d)$ via the inclusion
$\text{FM}^{\text{alg}}_n(\mathbb A^d)$ via the inclusion  $T_{d,n} \hookrightarrow~\text{FM}^{\text{alg}}_n(\mathbb A^d)$. Note that for each
$T_{d,n} \hookrightarrow~\text{FM}^{\text{alg}}_n(\mathbb A^d)$. Note that for each ![]() $I \in P_2({n})$ with
$I \in P_2({n})$ with ![]() $I \neq [n]$ the line bundle with section corresponding to the divisor
$I \neq [n]$ the line bundle with section corresponding to the divisor ![]() $D(I)$ pulls back to the line bundle with section corresponding to
$D(I)$ pulls back to the line bundle with section corresponding to ![]() $T_{d,n}(I)$ and for
$T_{d,n}(I)$ and for ![]() $I = [n]$ the pullback of the corresponding line bundle has the zero section. We will let
$I = [n]$ the pullback of the corresponding line bundle has the zero section. We will let ![]() $s_I\colon \mathcal O_{T_{d,n}}\to \mathcal O_{T_{d,n}}(I)$ denote the pullback of
$s_I\colon \mathcal O_{T_{d,n}}\to \mathcal O_{T_{d,n}}(I)$ denote the pullback of  $s_I\colon \mathcal O_{\text{FM}^{\text{alg}}_n(\mathbb A^d)} \to \mathcal O_{\text{FM}^{\text{alg}}_n(\mathbb A^d)}(D(I))$ for each
$s_I\colon \mathcal O_{\text{FM}^{\text{alg}}_n(\mathbb A^d)} \to \mathcal O_{\text{FM}^{\text{alg}}_n(\mathbb A^d)}(D(I))$ for each ![]() $I \in P_2({n})$.
$I \in P_2({n})$.
The operad composition morphisms of the ![]() $\text{\textbf{CGK}}_d$ operad do not extend to maps of log-schemes for the objects
$\text{\textbf{CGK}}_d$ operad do not extend to maps of log-schemes for the objects ![]() $\mathsf K_{d,n}$. Instead, in order to extend
$\mathsf K_{d,n}$. Instead, in order to extend ![]() $\text{\textbf{CGK}}_d$ to a (pseudo)-operad of log-schemes we must let its objects be the log-schemes
$\text{\textbf{CGK}}_d$ to a (pseudo)-operad of log-schemes we must let its objects be the log-schemes ![]() $\mathsf T_{d,n}$, whose log structures are given by one line bundle with section
$\mathsf T_{d,n}$, whose log structures are given by one line bundle with section ![]() $s_I\colon \mathcal O_{T_{d,n}}\to \mathcal O_{T_{d,n}}(I)$ for each non-empty
$s_I\colon \mathcal O_{T_{d,n}}\to \mathcal O_{T_{d,n}}(I)$ for each non-empty ![]() $I \subseteq [n]$ defined as above for
$I \subseteq [n]$ defined as above for ![]() $\vert I \vert\geq 2$ and defined by
$\vert I \vert\geq 2$ and defined by
 \begin{equation*}\mathcal O_{T_{d,n}}(\{i\}) := \bigotimes_{I \ni i} \mathcal O_{T_{d,n}}(I)^\vee,\end{equation*}
\begin{equation*}\mathcal O_{T_{d,n}}(\{i\}) := \bigotimes_{I \ni i} \mathcal O_{T_{d,n}}(I)^\vee,\end{equation*} with ![]() $s_{\{i\}} = 0$ for one element sets. For n = 1 we define
$s_{\{i\}} = 0$ for one element sets. For n = 1 we define ![]() $\mathcal O_{T_{d,1}}(\{1\}) := \mathcal O_{T_{d,1}}$ with the zero section.
$\mathcal O_{T_{d,1}}(\{1\}) := \mathcal O_{T_{d,1}}$ with the zero section.
5.2. The log geometric CGK operad
As mentioned, the symmetry and composition morphisms of the ![]() $\text{\textbf{CGK}}_d$ operad can be extended to morphisms of log schemes
$\text{\textbf{CGK}}_d$ operad can be extended to morphisms of log schemes ![]() $\mathsf T_{d,n}$. To see this for the symmetry morphisms note that, for
$\mathsf T_{d,n}$. To see this for the symmetry morphisms note that, for ![]() $\sigma \in \Sigma_n$ we have that the corresponding automorphism on
$\sigma \in \Sigma_n$ we have that the corresponding automorphism on ![]() $\text{FM}^{\text{alg}}_n(X)$, sends each divisor
$\text{FM}^{\text{alg}}_n(X)$, sends each divisor ![]() $D(I)$ isomorphically to
$D(I)$ isomorphically to ![]() $D(\sigma(I))$. This induces isomorphisms of line bundles (with sections)
$D(\sigma(I))$. This induces isomorphisms of line bundles (with sections)  $\sigma^*\mathcal O_{\text{FM}^{\text{alg}}_n(X)}(D(I)) \to \mathcal O_{\text{FM}^{\text{alg}}_n(X)}(D(\sigma^{-1}(I)))$. These maps extend the symmetry action on
$\sigma^*\mathcal O_{\text{FM}^{\text{alg}}_n(X)}(D(I)) \to \mathcal O_{\text{FM}^{\text{alg}}_n(X)}(D(\sigma^{-1}(I)))$. These maps extend the symmetry action on ![]() $\text{FM}^{\text{alg}}_n(X)$ to a symmetry action on
$\text{FM}^{\text{alg}}_n(X)$ to a symmetry action on ![]() $\text{FM}^{\text{log}}_n(X)$. This in turn gives symmetry actions on
$\text{FM}^{\text{log}}_n(X)$. This in turn gives symmetry actions on ![]() $\mathsf K_{d,n}$ and
$\mathsf K_{d,n}$ and ![]() $\mathsf T_{d,n}$ in the same way.
$\mathsf T_{d,n}$ in the same way.
Extending the composition morphisms is slightly trickier. Again, let n be a positive integer and let ![]() $q\colon M\twoheadrightarrow [n]$ be a surjection of sets. As before, let
$q\colon M\twoheadrightarrow [n]$ be a surjection of sets. As before, let ![]() $\pi_0\colon T_{d,n}\times \prod_{i=1}^n T_{d,q^{-1}(i)} \to T_{d,n}$ and
$\pi_0\colon T_{d,n}\times \prod_{i=1}^n T_{d,q^{-1}(i)} \to T_{d,n}$ and ![]() $\pi_r \colon T_{d,n}\times \prod_{i=1}^n T_{d,q^{-1}(i)} \to T_{d,q^{-1}(r)}$ denote the corresponding projections, and let
$\pi_r \colon T_{d,n}\times \prod_{i=1}^n T_{d,q^{-1}(i)} \to T_{d,q^{-1}(r)}$ denote the corresponding projections, and let
 \begin{equation*}\gamma \colon T_{d,n}\times \prod_{i=1}^n T_{d,q^{-1}(i)} \to T_{d,M}\end{equation*}
\begin{equation*}\gamma \colon T_{d,n}\times \prod_{i=1}^n T_{d,q^{-1}(i)} \to T_{d,M}\end{equation*} be the composition morphism of ![]() $\text{\textbf{CGK}}_d$. We can immediately show the following.
$\text{\textbf{CGK}}_d$. We can immediately show the following.
Lemma 5.3. Let ![]() $I \subsetneq M$ with
$I \subsetneq M$ with ![]() $\vert I \vert \geq 2$. Then there is a unique isomorphism of line bundles with sections
$\vert I \vert \geq 2$. Then there is a unique isomorphism of line bundles with sections
(a)
 $\gamma^*\mathcal O_{T_{d,M}}(I) \xrightarrow{\cong} \pi_r^*\mathcal O_{T_{d,q^{-1}(r)}}(I)$ if
$\gamma^*\mathcal O_{T_{d,M}}(I) \xrightarrow{\cong} \pi_r^*\mathcal O_{T_{d,q^{-1}(r)}}(I)$ if  $I \subsetneq q^{-1}(r)$.
$I \subsetneq q^{-1}(r)$.(b)
 $\gamma^*\mathcal O_{T_{d,M}}(I) \xrightarrow{\cong} \pi_0^*\mathcal O_{T_{d,n}}(q(I))$ if
$\gamma^*\mathcal O_{T_{d,M}}(I) \xrightarrow{\cong} \pi_0^*\mathcal O_{T_{d,n}}(q(I))$ if  $I = \bigsqcup_{i\in q(I)} q^{-1}(r)$ and
$I = \bigsqcup_{i\in q(I)} q^{-1}(r)$ and  $q(I)\geq 2$.
$q(I)\geq 2$.(c)
 $\gamma^*\mathcal O_{T_{d,M}}(I) \xrightarrow{\cong} \mathcal O_{T_{d,n}\times \prod T_{d,q^{-1}(i)}}$, where the right hand side is taken with the unit section, if
$\gamma^*\mathcal O_{T_{d,M}}(I) \xrightarrow{\cong} \mathcal O_{T_{d,n}\times \prod T_{d,q^{-1}(i)}}$, where the right hand side is taken with the unit section, if  $(I,q^{-1}(1),\dots,q^{-1}(n))$ are not nested, i.e.
$(I,q^{-1}(1),\dots,q^{-1}(n))$ are not nested, i.e.  $I$ is not contained in any
$I$ is not contained in any  $q^{-1}(r)$ and also not equal to a union of any collection of
$q^{-1}(r)$ and also not equal to a union of any collection of  $q^{-1}(r)$.
$q^{-1}(r)$.
Proof. Cases (a) and (b) follow directly from corollary 4.11 and lemma 5.1. Case (c) follows from the fact that the image of ![]() $\gamma$ is
$\gamma$ is ![]() $T_{d,M}(q^{-1}(1), \dots, q^{-1}(n))$ (proposition 4.10) which is disjoint with
$T_{d,M}(q^{-1}(1), \dots, q^{-1}(n))$ (proposition 4.10) which is disjoint with ![]() $T_{d,M}(I)$ since
$T_{d,M}(I)$ since ![]() $T_{d,M}(I,q^{-1}(1),\dots,q^{-1}(n))$ is empty by the nestedness criterion.
$T_{d,M}(I,q^{-1}(1),\dots,q^{-1}(n))$ is empty by the nestedness criterion.
This alone is almost enough to extend the operad composition morphisms to maps of corresponding log-schemes but we must also express ![]() $\gamma^* \mathcal O_{T_{d,M}}(I)$ as a tensor product of the line bundles on
$\gamma^* \mathcal O_{T_{d,M}}(I)$ as a tensor product of the line bundles on ![]() $T_{d,n}\times \prod_{i=1}^n T_{d,q^{-1}(i)}$ for
$T_{d,n}\times \prod_{i=1}^n T_{d,q^{-1}(i)}$ for ![]() $I=M$,
$I=M$, ![]() $I= q^{-1}(r)$, and
$I= q^{-1}(r)$, and ![]() $\vert I \vert = 1$. Note that in all of these cases the pullback of the sections of these corresponding line bundles are all 0. To this end, recall that that lemma 4.8 gives isomorphisms of line bundles on
$\vert I \vert = 1$. Note that in all of these cases the pullback of the sections of these corresponding line bundles are all 0. To this end, recall that that lemma 4.8 gives isomorphisms of line bundles on ![]() $T_{d,n}$
$T_{d,n}$
 \begin{equation*}\mathcal M_I \xrightarrow{\cong} \bigotimes_{I \subseteq I'} \mathcal O_{T_{d,n}}(I')^\vee,\end{equation*}
\begin{equation*}\mathcal M_I \xrightarrow{\cong} \bigotimes_{I \subseteq I'} \mathcal O_{T_{d,n}}(I')^\vee,\end{equation*} where ![]() $\mathcal M_I$ are the line bundles of the universal simple screen on
$\mathcal M_I$ are the line bundles of the universal simple screen on ![]() $T_{d,n}$ (section 4.3), such that the following diagram commutes for every
$T_{d,n}$ (section 4.3), such that the following diagram commutes for every ![]() $I\subseteq J$,
$I\subseteq J$,

where the bottom arrow is the map
 \begin{equation*}\bigotimes_{I\subseteq I',\ J\not \subseteq I'} s_{I'}^\vee.\end{equation*}
\begin{equation*}\bigotimes_{I\subseteq I',\ J\not \subseteq I'} s_{I'}^\vee.\end{equation*}In particular, this means that we have isomorphisms
 \begin{equation*}\mathcal O_{T_{d,n}}(I) \cong \mathcal M_I^\vee \bigotimes_{I \subsetneq I'} \mathcal O_{T_{d,n}}(I)^\vee.\end{equation*}
\begin{equation*}\mathcal O_{T_{d,n}}(I) \cong \mathcal M_I^\vee \bigotimes_{I \subsetneq I'} \mathcal O_{T_{d,n}}(I)^\vee.\end{equation*}Lemma 5.4. There are canonical isomorphisms of line bundles
(a)
 $\gamma^*\mathcal O_{T_{d,M}}(M) \xrightarrow{\cong} \pi_0^*\mathcal O_{T_{d,n}}([n])$.
$\gamma^*\mathcal O_{T_{d,M}}(M) \xrightarrow{\cong} \pi_0^*\mathcal O_{T_{d,n}}([n])$.(b)
 $\gamma^*\mathcal O_{T_{d,M}}(q^{-1}(r)) \xrightarrow{\cong} \pi_0^*\mathcal O_{T_{d,n}}(\{r\}) \otimes \pi_r^*\mathcal O_{T_{d,q^{-1}(r)}}(q^{-1}(r))$.
$\gamma^*\mathcal O_{T_{d,M}}(q^{-1}(r)) \xrightarrow{\cong} \pi_0^*\mathcal O_{T_{d,n}}(\{r\}) \otimes \pi_r^*\mathcal O_{T_{d,q^{-1}(r)}}(q^{-1}(r))$.(c)
 $\gamma^*\mathcal O_{T_{d,M}}(\{i\}) \xrightarrow{\cong} \pi_r^*\mathcal O_{T_{d,q^{-1}(r)}}(\{i\})$, if
$\gamma^*\mathcal O_{T_{d,M}}(\{i\}) \xrightarrow{\cong} \pi_r^*\mathcal O_{T_{d,q^{-1}(r)}}(\{i\})$, if  $i\in q^{-1}(r)$.
$i\in q^{-1}(r)$.
Proof. First note that by the above we have  $\mathcal O_{T_{d,M}}(M) \cong \mathcal (M_{M}^{d,M})^\vee$. By Corollary 4.12 we have
$\mathcal O_{T_{d,M}}(M) \cong \mathcal (M_{M}^{d,M})^\vee$. By Corollary 4.12 we have  $\gamma^*\mathcal M_{M}^{d,M} \cong \pi_0^*\mathcal M_{[n]}^{d,n}$. From this part (a) follows. For part (b) note that lemma 5.3 gives an isomorphism
$\gamma^*\mathcal M_{M}^{d,M} \cong \pi_0^*\mathcal M_{[n]}^{d,n}$. From this part (a) follows. For part (b) note that lemma 5.3 gives an isomorphism
 \begin{equation*}\bigotimes_{q^{-1}(r)\subsetneq S} \gamma^*\mathcal O_{T_{d,M}}(I) \cong \gamma^*\mathcal O_{T_{d,M}}(M)\bigotimes_{r\in J \subsetneq [n]} \pi_0^*\mathcal O_{T_{d,n}}(J) \cong \bigotimes_{r\in J \subseteq [n]} \pi_0^*\mathcal O_{T_{d,n}}(J)\end{equation*}
\begin{equation*}\bigotimes_{q^{-1}(r)\subsetneq S} \gamma^*\mathcal O_{T_{d,M}}(I) \cong \gamma^*\mathcal O_{T_{d,M}}(M)\bigotimes_{r\in J \subsetneq [n]} \pi_0^*\mathcal O_{T_{d,n}}(J) \cong \bigotimes_{r\in J \subseteq [n]} \pi_0^*\mathcal O_{T_{d,n}}(J)\end{equation*} where the last isomorphism follows from part (a). By definition, this is just ![]() $\pi_0^*\mathcal O_{T_{d,n}}(\{r\})^\vee$ and so we get an isomorphism
$\pi_0^*\mathcal O_{T_{d,n}}(\{r\})^\vee$ and so we get an isomorphism
 \begin{align*}\gamma^* \mathcal O_{T_{d,M}}(q^{-1}(r)) &\xrightarrow{\cong} \gamma^*(\mathcal M_{q^{-1}(r)}^{d,M})^\vee \bigotimes_{q^{-1}(r)\subsetneq I'} \mathcal \gamma^*O_{T_{d,M}}(I')^\vee\\ &\xrightarrow{\cong}\pi_r^*\mathcal O_{T_{d,q^{-1}(r)}}(q^{-1}(r))\otimes \pi_0^*\mathcal O_{T_{d,q^{-1}(r)}}(\{r\}).\end{align*}
\begin{align*}\gamma^* \mathcal O_{T_{d,M}}(q^{-1}(r)) &\xrightarrow{\cong} \gamma^*(\mathcal M_{q^{-1}(r)}^{d,M})^\vee \bigotimes_{q^{-1}(r)\subsetneq I'} \mathcal \gamma^*O_{T_{d,M}}(I')^\vee\\ &\xrightarrow{\cong}\pi_r^*\mathcal O_{T_{d,q^{-1}(r)}}(q^{-1}(r))\otimes \pi_0^*\mathcal O_{T_{d,q^{-1}(r)}}(\{r\}).\end{align*}This gives part (b). Part (c) follows from a similar argument.
Remark. If n = 1 the left hand sides of (a) and (b) are equal. In this case, both statements are true but we must choose (b) to be the isomorphism defining our map of log schemes for the operad axioms to be satisfied. Similarly, if ![]() $\vert q^{-1}(r) \vert = 1$ we must also choose the map in (b).
$\vert q^{-1}(r) \vert = 1$ we must also choose the map in (b).
With this we have defined isomorphisms of line bundles extending the operad composition maps of ![]() $\text{\textbf{CGK}}_d$ to morphisms of log-schemes
$\text{\textbf{CGK}}_d$ to morphisms of log-schemes
 \begin{equation*}\gamma^{\log} \colon \mathsf T_{d,n}\times \prod_{i=1}^n \mathsf T_{d,q^{-1}(i)} \to \mathsf T_{d,M}.\end{equation*}
\begin{equation*}\gamma^{\log} \colon \mathsf T_{d,n}\times \prod_{i=1}^n \mathsf T_{d,q^{-1}(i)} \to \mathsf T_{d,M}.\end{equation*}Unfortunately, there are no maps of log schemes
 \begin{equation*}\text{Spec } \mathbb{k} \to (\text{Spec } \mathbb{k} ,\mathcal O_{\mathbb{k}} \xrightarrow{0} \mathcal O_{\mathbb{k}})\end{equation*}
\begin{equation*}\text{Spec } \mathbb{k} \to (\text{Spec } \mathbb{k} ,\mathcal O_{\mathbb{k}} \xrightarrow{0} \mathcal O_{\mathbb{k}})\end{equation*} and therefore we cannot extend our unit map to a map of log schemes. However, it is easy to verify that despite this the ![]() $\circ_i$-operations,
$\circ_i$-operations,  $T_{d,n}\times T_{d,m} \xrightarrow{\circ_i} T_{d,m+n-1}$, do extend to maps of log schemes
$T_{d,n}\times T_{d,m} \xrightarrow{\circ_i} T_{d,m+n-1}$, do extend to maps of log schemes  $\mathsf T_{d,n}\times \mathsf T_{d,m} \xrightarrow{\circ_i} \mathsf T_{d,m+n-1}$. One can verify that these maps, together with the symmetry morphisms satisfy the pseudo-operad axioms.
$\mathsf T_{d,n}\times \mathsf T_{d,m} \xrightarrow{\circ_i} \mathsf T_{d,m+n-1}$. One can verify that these maps, together with the symmetry morphisms satisfy the pseudo-operad axioms.
Definition 5.5. The log-geometric Chen, Gibney, Krashen pseudo-operad,  $\text{\textbf{CGK}}^{\log}_d$ is the pseudo-operad with objects
$\text{\textbf{CGK}}^{\log}_d$ is the pseudo-operad with objects ![]() $\mathsf T_{d,n}$ and with morphisms as described above.
$\mathsf T_{d,n}$ and with morphisms as described above.
Remark. In the case d = 1 this is isomorphic to the framed little curves pseudo-operad constructed by Vaintrob in [Reference Vaintrob27].
5.3. Kato–Nakayama analytifications
In this section we show that the Kato–Nakayama Analytification of  $\text{\textbf{CGK}}^{\log}_d$ is homeomorphic to the
$\text{\textbf{CGK}}^{\log}_d$ is homeomorphic to the ![]() $S^1$-framed Fulton–MacPherson operad in dimension 2d,
$S^1$-framed Fulton–MacPherson operad in dimension 2d, ![]() $\text{\textbf{FM}}_{2d}\rtimes S^1$, which in turn is a model for the
$\text{\textbf{FM}}_{2d}\rtimes S^1$, which in turn is a model for the ![]() $S^1$-framed little 2d-disks operad
$S^1$-framed little 2d-disks operad ![]() $\text{\textbf{LD}}_{2d} \rtimes S^1$ as mentioned in section 3.
$\text{\textbf{LD}}_{2d} \rtimes S^1$ as mentioned in section 3.
We begin by showing that there is a homeomorphism of spaces over ![]() $X^n(\mathbb C)$,
$X^n(\mathbb C)$,
 \begin{equation*}\text{FM}^{\text{log}}_n(X)^\text{KN} \cong~\text{FM}^\text{top}_n(X(\mathbb C)),\end{equation*}
\begin{equation*}\text{FM}^{\text{log}}_n(X)^\text{KN} \cong~\text{FM}^\text{top}_n(X(\mathbb C)),\end{equation*} which commutes with the corresponding inclusions of ![]() $\text{Conf} _n(X(\mathbb C))$. The rough idea behind our proof of this statement is that the left hand side is the Kato–Nakayama space of a sequence of logarithmic blow-ups of
$\text{Conf} _n(X(\mathbb C))$. The rough idea behind our proof of this statement is that the left hand side is the Kato–Nakayama space of a sequence of logarithmic blow-ups of ![]() $X^n$ and the right hand side is a sequence of real blow-ups of
$X^n$ and the right hand side is a sequence of real blow-ups of ![]() $X(\mathbb C)^n$ and under sufficiently nice circumstances these two agree.
$X(\mathbb C)^n$ and under sufficiently nice circumstances these two agree.
Definition 5.6. Let ![]() $\mathsf X = (X, \mathfrak L)$ be a log scheme and let
$\mathsf X = (X, \mathfrak L)$ be a log scheme and let ![]() $Y$ be a closed subscheme of
$Y$ be a closed subscheme of ![]() $X$. Then we let
$X$. Then we let  $\mathrm{Bl}^{\log}_{Y} \mathsf X$ denote the log scheme with underlying scheme
$\mathrm{Bl}^{\log}_{Y} \mathsf X$ denote the log scheme with underlying scheme ![]() $\mathrm{Bl}_{Y}\ X$ and log structure given by the log structure
$\mathrm{Bl}_{Y}\ X$ and log structure given by the log structure ![]() $\mathfrak L$ pulled back to
$\mathfrak L$ pulled back to ![]() $\mathrm{Bl}_{Y}\ X$ and the line bundle with section corresponding to the exceptional divisor of the blow-up. We also define the blow-down map,
$\mathrm{Bl}_{Y}\ X$ and the line bundle with section corresponding to the exceptional divisor of the blow-up. We also define the blow-down map,  $\mathrm{Bl}^{\log}_{Y} \mathsf X \to X$ to be given by the normal blow-down map on underlying schemes and by “forgetting” the added line bundle with section.
$\mathrm{Bl}^{\log}_{Y} \mathsf X \to X$ to be given by the normal blow-down map on underlying schemes and by “forgetting” the added line bundle with section.
Proposition 5.7. Let ![]() $X$ be a smooth
$X$ be a smooth ![]() $\mathbb C$-variety and let
$\mathbb C$-variety and let ![]() $Y$ be a smooth subvariety of codimension k. If Y is the zero locus of a section of a rank k vector bundle on X then there is an isomorphism of spaces over
$Y$ be a smooth subvariety of codimension k. If Y is the zero locus of a section of a rank k vector bundle on X then there is an isomorphism of spaces over ![]() $X(\mathbb C)$
$X(\mathbb C)$
 \begin{equation*}(\mathrm{Bl}^{\log}_{Y}X)^{\text{KN}}\cong~\mathrm{Bl}^{\mathbb{R}}_{Y(\mathbb C)}\ X(\mathbb C).\end{equation*}
\begin{equation*}(\mathrm{Bl}^{\log}_{Y}X)^{\text{KN}}\cong~\mathrm{Bl}^{\mathbb{R}}_{Y(\mathbb C)}\ X(\mathbb C).\end{equation*}Proof. This isomorphism is easy to construct when ![]() $Y$ is a complete intersection, i.e. the zero locus of a section of
$Y$ is a complete intersection, i.e. the zero locus of a section of  $\mathcal O^{\oplus k}_X$. The general case follows by gluing.
$\mathcal O^{\oplus k}_X$. The general case follows by gluing.
Corollary 5.8. Let ![]() $\mathsf X = (X,\mathfrak L)$ be a log-scheme whose log structure is given by line bundles with sections cutting out smooth divisors
$\mathsf X = (X,\mathfrak L)$ be a log-scheme whose log structure is given by line bundles with sections cutting out smooth divisors ![]() $D_1,\dots, D_n$ such that
$D_1,\dots, D_n$ such that ![]() $D_1\cup \dots \cup D_n$ is a strict normal crossings divisor and let
$D_1\cup \dots \cup D_n$ is a strict normal crossings divisor and let ![]() $Y$ be as in the proposition with the additional constraint that
$Y$ be as in the proposition with the additional constraint that ![]() $Y$ intersects all intersections
$Y$ intersects all intersections ![]() $D_{i_1}\cap \dots D_{i_k}$ transversally. Then there is an isomorphism of spaces over
$D_{i_1}\cap \dots D_{i_k}$ transversally. Then there is an isomorphism of spaces over ![]() $\mathsf X^{\text{KN}}$
$\mathsf X^{\text{KN}}$
 \begin{equation*}(\mathrm{Bl}^{\log}_{Y}X)^{\text{KN}}\cong~\mathrm{Bl}^{\mathbb{R}}_{\tilde Y}\ \mathsf X^{\text{KN}}\end{equation*}
\begin{equation*}(\mathrm{Bl}^{\log}_{Y}X)^{\text{KN}}\cong~\mathrm{Bl}^{\mathbb{R}}_{\tilde Y}\ \mathsf X^{\text{KN}}\end{equation*} where ![]() $\tilde Y$ denotes the strict transform of
$\tilde Y$ denotes the strict transform of ![]() $Y(\mathbb C)$ under the sequence of blow-down maps
$Y(\mathbb C)$ under the sequence of blow-down maps
Proof. Let ![]() $t\colon \mathcal O_X \to \mathcal V$ denote the vector bundle section cutting out
$t\colon \mathcal O_X \to \mathcal V$ denote the vector bundle section cutting out ![]() $Y$. It is clear from the proposition that there is an isomorphism
$Y$. It is clear from the proposition that there is an isomorphism
 \begin{equation*}(\mathrm{Bl}^{\log}_{Y}X)^{\text{KN}}\cong~\mathrm{Bl}^{\mathbb{R}}_{\tilde t}\ \mathsf X^{\text{KN}}\end{equation*}
\begin{equation*}(\mathrm{Bl}^{\log}_{Y}X)^{\text{KN}}\cong~\mathrm{Bl}^{\mathbb{R}}_{\tilde t}\ \mathsf X^{\text{KN}}\end{equation*} where ![]() $\tilde t$ denotes the pullback (i.e. total transform) to
$\tilde t$ denotes the pullback (i.e. total transform) to ![]() $\mathsf X^\text{KN}$ of the vector bundle section t seen as a section of a topological vector bundle
$\mathsf X^\text{KN}$ of the vector bundle section t seen as a section of a topological vector bundle ![]() $t \in \Gamma(X(\mathbb C),{\mathcal V})$. The transversallity conditions for intersections with
$t \in \Gamma(X(\mathbb C),{\mathcal V})$. The transversallity conditions for intersections with ![]() $Y$ imply that
$Y$ imply that ![]() $\tilde Y$ is the zero locus of the section
$\tilde Y$ is the zero locus of the section ![]() $\tilde t$. This completes the proof.
$\tilde t$. This completes the proof.
Proposition 5.9. There is a unique homeomorphism of spaces over ![]() $X^n(\mathbb C)$,
$X^n(\mathbb C)$,
 \begin{equation*}\text{FM}^{\text{log}}_n(X)^\text{KN} \cong~\text{FM}^\text{top}_n(X(\mathbb C)),\end{equation*}
\begin{equation*}\text{FM}^{\text{log}}_n(X)^\text{KN} \cong~\text{FM}^\text{top}_n(X(\mathbb C)),\end{equation*} which commutes with the corresponding inclusions of ![]() $\text{Conf} _n(X(\mathbb C))$.
$\text{Conf} _n(X(\mathbb C))$.
Proof. First, recall from [Reference Li18] that the Fulton–MacPherson space ![]() $\text{FM}^{\text{alg}}_n(X)$ is isomorphic to the sequence of blow-ups
$\text{FM}^{\text{alg}}_n(X)$ is isomorphic to the sequence of blow-ups
 \begin{equation*}\mathrm{Bl}_{\tilde \Delta_{I_N}}\ \dots~\mathrm{Bl}_{\tilde \Delta_{I_1}}\ X^n\end{equation*}
\begin{equation*}\mathrm{Bl}_{\tilde \Delta_{I_N}}\ \dots~\mathrm{Bl}_{\tilde \Delta_{I_1}}\ X^n\end{equation*} where ![]() $I_1, \dots, I_N$ are the sets in
$I_1, \dots, I_N$ are the sets in ![]() $P_2({[n]})$ in any order satisfying the conditions of theorem 1.3 in [Reference Li18] and
$P_2({[n]})$ in any order satisfying the conditions of theorem 1.3 in [Reference Li18] and ![]() $\tilde \Delta_{I_i}$ denotes the dominant transform of the diagonal
$\tilde \Delta_{I_i}$ denotes the dominant transform of the diagonal ![]() $\Delta_{I_i} \subseteq X^n$ under all previous blow-ups. Furthermore, recall that the divisors
$\Delta_{I_i} \subseteq X^n$ under all previous blow-ups. Furthermore, recall that the divisors ![]() $D(I_i)$ are the dominant transforms of the exceptional divisor
$D(I_i)$ are the dominant transforms of the exceptional divisor ![]() $\tilde D(I_i)$ from the blow-up
$\tilde D(I_i)$ from the blow-up
 \begin{equation*}\mathrm{Bl}_{\tilde \Delta_{I_i}}~\mathrm{Bl}_{\tilde \Delta_{I_{i-1}}}\ \dots~\mathrm{Bl}_{\tilde \Delta_{I_1}}\ X^n \to~\mathrm{Bl}_{\tilde \Delta_{I_{i-1}}}\ \dots~\mathrm{Bl}_{\tilde \Delta_{I_1}}\ X^n\end{equation*}
\begin{equation*}\mathrm{Bl}_{\tilde \Delta_{I_i}}~\mathrm{Bl}_{\tilde \Delta_{I_{i-1}}}\ \dots~\mathrm{Bl}_{\tilde \Delta_{I_1}}\ X^n \to~\mathrm{Bl}_{\tilde \Delta_{I_{i-1}}}\ \dots~\mathrm{Bl}_{\tilde \Delta_{I_1}}\ X^n\end{equation*} taken under all subsequent blow-ups  $\mathrm{Bl}_{\tilde \Delta_{I_N}}\ \dots\mathrm{Bl}_{\tilde \Delta_{I_{i+1}}}\ $. Additionally, the topological Fulton–MacPherson space
$\mathrm{Bl}_{\tilde \Delta_{I_N}}\ \dots\mathrm{Bl}_{\tilde \Delta_{I_{i+1}}}\ $. Additionally, the topological Fulton–MacPherson space ![]() $\text{FM}^\text{top}_n(X(\mathbb C))$ can also be written as a sequence of real oriented blow-ups of
$\text{FM}^\text{top}_n(X(\mathbb C))$ can also be written as a sequence of real oriented blow-ups of ![]() $X^n(\mathbb C)$ in its diagonals in a similar manner.
$X^n(\mathbb C)$ in its diagonals in a similar manner.
The proposition would now follow from corollary 5.8 by induction if there was an ordering ![]() $I_1, \dots, I_N$ of the sets in
$I_1, \dots, I_N$ of the sets in ![]() $P_2({[n]})$ satisfying the aforementioned conditions such that for every
$P_2({[n]})$ satisfying the aforementioned conditions such that for every ![]() $1\leq i \leq n$
$1\leq i \leq n$
 \begin{equation*}\tilde \Delta_{I_{i+1}} \subseteq~\mathrm{Bl}_{\tilde \Delta_{I_i}}~\mathrm{Bl}_{\tilde \Delta_{I_{i-1}}}\ \dots~\mathrm{Bl}_{\tilde \Delta_{I_1}}\ X^n\end{equation*}
\begin{equation*}\tilde \Delta_{I_{i+1}} \subseteq~\mathrm{Bl}_{\tilde \Delta_{I_i}}~\mathrm{Bl}_{\tilde \Delta_{I_{i-1}}}\ \dots~\mathrm{Bl}_{\tilde \Delta_{I_1}}\ X^n\end{equation*} meets any intersection of the divisors ![]() $\tilde D(I_1) \dots \tilde D(I_i)$ transversally. It is not hard to show that any ordering where the sets
$\tilde D(I_1) \dots \tilde D(I_i)$ transversally. It is not hard to show that any ordering where the sets ![]() $I\in P_2({[n]})$ appear in decreasing order of size, i.e.
$I\in P_2({[n]})$ appear in decreasing order of size, i.e. ![]() $\vert I_i \vert\geq \vert I_{i+1} \vert$, satisfies all criteria and thus we are done.
$\vert I_i \vert\geq \vert I_{i+1} \vert$, satisfies all criteria and thus we are done.
Remark. Note that the transversality conditions here are not implied by the arrangement conditions in theorem 1.3 of [Reference Li18]. Hence, there is no obvious analogue of the above proposition for general wonderful compactifications.
Corollary 5.10. There are isomorphisms
•
 $\text{FM}^{\text{log}}_n(X)^\text{KN} \cong~\text{FM}^\text{top}_n(X(\mathbb C))$
$\text{FM}^{\text{log}}_n(X)^\text{KN} \cong~\text{FM}^\text{top}_n(X(\mathbb C))$•
 $\mathsf K_{d,n}^\text{KN} \cong~\text{K}_{2d,n}$
$\mathsf K_{d,n}^\text{KN} \cong~\text{K}_{2d,n}$•
 $\mathsf T_{d,n} \cong (S^1)^n\times~\text{K}_{2d,n}$
$\mathsf T_{d,n} \cong (S^1)^n\times~\text{K}_{2d,n}$
which commute with all relevant maps, i.e. inclusions of ![]() $\text{Conf} _n(X(\mathbb C))$, maps to
$\text{Conf} _n(X(\mathbb C))$, maps to ![]() $X^n(\mathbb C)$, inclusions of fibres, etc.
$X^n(\mathbb C)$, inclusions of fibres, etc.
Proof. We have already constructed the isomorphism  $\text{FM}^{\text{log}}_n(X)^\text{KN} \cong~\text{FM}^\text{top}_n(X(\mathbb C))$. Since the morphism
$\text{FM}^{\text{log}}_n(X)^\text{KN} \cong~\text{FM}^\text{top}_n(X(\mathbb C))$. Since the morphism  $\mathsf K_{d,n} \hookrightarrow~\text{FM}^{\text{log}}_n(\mathbb A^d)$ is strict, the top square in the following diagram is Cartesian.
$\mathsf K_{d,n} \hookrightarrow~\text{FM}^{\text{log}}_n(\mathbb A^d)$ is strict, the top square in the following diagram is Cartesian.

We already know that the bottom square is Cartesian and thus the entire diagram is Cartesian, i.e.  $\mathsf K_{d,n}^\text{KN} \to (\text{FM}^{\text{log}}_n(\mathbb A^d))^{\text{KN}}$ is the inclusion of the fibre over the origin in
$\mathsf K_{d,n}^\text{KN} \to (\text{FM}^{\text{log}}_n(\mathbb A^d))^{\text{KN}}$ is the inclusion of the fibre over the origin in ![]() $(\mathbb C^d)^n$ and thus
$(\mathbb C^d)^n$ and thus  $(\text{FM}^{\text{log}}_n(\mathbb A^d))^\text{KN} \cong~\text{FM}^\text{top}_n(\mathbb C^d)$ restricts to an isomorphism
$(\text{FM}^{\text{log}}_n(\mathbb A^d))^\text{KN} \cong~\text{FM}^\text{top}_n(\mathbb C^d)$ restricts to an isomorphism  $\mathsf K_{d,n}^\text{KN} \cong~\text{K}_{2d,n}.$ Notice that we get 2d on the right hand side since
$\mathsf K_{d,n}^\text{KN} \cong~\text{K}_{2d,n}.$ Notice that we get 2d on the right hand side since ![]() $\mathbb C\cong \mathbb R^2$. Furthermore, we know that
$\mathbb C\cong \mathbb R^2$. Furthermore, we know that
 \begin{equation*}\mathsf T_{d,n}^\text{KN} =~\mathrm{Bl}^{\mathbb{R}}_{0\in \mathcal O(\{1\})}\ \dots\mathrm{Bl}^{\mathbb{R}}_{0\in \mathcal O(\{n\})}\ \mathsf K_{d,n}^\text{KN}.\end{equation*}
\begin{equation*}\mathsf T_{d,n}^\text{KN} =~\mathrm{Bl}^{\mathbb{R}}_{0\in \mathcal O(\{1\})}\ \dots\mathrm{Bl}^{\mathbb{R}}_{0\in \mathcal O(\{n\})}\ \mathsf K_{d,n}^\text{KN}.\end{equation*} By corollary 2.6 this is homeomorphic to ![]() $(S^1)^n\times~\text{K}_{2d,n},$ i.e. the nth space in the
$(S^1)^n\times~\text{K}_{2d,n},$ i.e. the nth space in the ![]() $\text{\textbf{FM}}_{2d}\rtimes S^1$ operad. It is easy to show that these choices of isomorphisms make all relevant maps commute as claimed.
$\text{\textbf{FM}}_{2d}\rtimes S^1$ operad. It is easy to show that these choices of isomorphisms make all relevant maps commute as claimed.
Next, we will show that the maps  $f_I\colon~\text{FM}^\text{top}_n(X(\mathbb C)) \to~\mathrm{Bl}^{\mathbb{R}}_{\Delta_I}\ X^I$,
$f_I\colon~\text{FM}^\text{top}_n(X(\mathbb C)) \to~\mathrm{Bl}^{\mathbb{R}}_{\Delta_I}\ X^I$,  $\pi_I\colon~\text{K}_{2d,n} \to S^{2d(\vert I \vert-1)-1}$ (which were defined in section 3) and the projections to the
$\pi_I\colon~\text{K}_{2d,n} \to S^{2d(\vert I \vert-1)-1}$ (which were defined in section 3) and the projections to the ![]() $S^1$ components
$S^1$ components ![]() $\pi_i\colon (S^1)^n\times~\text{K}_{2d,n} \to S^1$ are all identified with analytifications of explicit maps of corresponding log schemes under the isomorphisms described in the proof of corollary 5.10.
$\pi_i\colon (S^1)^n\times~\text{K}_{2d,n} \to S^1$ are all identified with analytifications of explicit maps of corresponding log schemes under the isomorphisms described in the proof of corollary 5.10.
Let ![]() $\mathsf S_{m}$ denote the log scheme
$\mathsf S_{m}$ denote the log scheme ![]() $(\mathbb P^m, 0\colon \mathcal O \to \mathcal O(-1))$. Its Kato–Nakayama space
$(\mathbb P^m, 0\colon \mathcal O \to \mathcal O(-1))$. Its Kato–Nakayama space ![]() $\mathsf S_m^{\text{KN}}$ homeomorphic to
$\mathsf S_m^{\text{KN}}$ homeomorphic to ![]() $S^{2m+1}$ and the map
$S^{2m+1}$ and the map ![]() $S^{2m+1}\cong S_m^{\text{KN}} \to \mathbb P^m(\mathbb C)$ is the Hopf fibration (proving this using proposition 5.7 may provide some insight into the idea behind the arguments to come). Recall from section 4.1 that the composition
$S^{2m+1}\cong S_m^{\text{KN}} \to \mathbb P^m(\mathbb C)$ is the Hopf fibration (proving this using proposition 5.7 may provide some insight into the idea behind the arguments to come). Recall from section 4.1 that the composition
factors via a map ![]() $f_I \colon~\text{FM}^{\text{alg}}_n(X) \to~\mathrm{Bl}_{\Delta_I}\ X^I$ for any
$f_I \colon~\text{FM}^{\text{alg}}_n(X) \to~\mathrm{Bl}_{\Delta_I}\ X^I$ for any ![]() $I \in P_2({n})$, and furthermore that there is an isomorphism of line bundles with sections
$I \in P_2({n})$, and furthermore that there is an isomorphism of line bundles with sections
 \begin{equation*}f_I^*\mathcal O(E_{\Delta_I}) \cong \bigotimes_{I \subseteq I'}\mathcal O(D(I')).\end{equation*}
\begin{equation*}f_I^*\mathcal O(E_{\Delta_I}) \cong \bigotimes_{I \subseteq I'}\mathcal O(D(I')).\end{equation*}This isomorphism defines a map of log schemes
 \begin{equation*}f_I^{\log}\colon~\text{FM}^{\text{log}}_n(X) \to~\mathrm{Bl}^{\log}_{\Delta_I}X^I.\end{equation*}
\begin{equation*}f_I^{\log}\colon~\text{FM}^{\text{log}}_n(X) \to~\mathrm{Bl}^{\log}_{\Delta_I}X^I.\end{equation*} Also recall that the fibre over the origin for the blow-down map ![]() $\mathrm{Bl}_{\Delta_I}\ X^I \to X^I$ is
$\mathrm{Bl}_{\Delta_I}\ X^I \to X^I$ is ![]() $\mathbb P^{d(\vert I \vert-1)-1}$ and that, if i denotes the inclusion of this fibre, we have that
$\mathbb P^{d(\vert I \vert-1)-1}$ and that, if i denotes the inclusion of this fibre, we have that ![]() $i^* \mathcal O(E_{\Delta_I}) \cong \mathcal O(-1)$. This means that
$i^* \mathcal O(E_{\Delta_I}) \cong \mathcal O(-1)$. This means that  $\mathsf S_{d(\vert I \vert-1)-1} = (\mathbb P^{d(\vert I \vert-1)-1}, 0\colon \mathcal O \to \mathcal O(-1))$ is the fibre over the origin of the log blow-down map
$\mathsf S_{d(\vert I \vert-1)-1} = (\mathbb P^{d(\vert I \vert-1)-1}, 0\colon \mathcal O \to \mathcal O(-1))$ is the fibre over the origin of the log blow-down map  $\mathrm{Bl}^{\log}_{\Delta_I} X^I \to X^I$ and
$\mathrm{Bl}^{\log}_{\Delta_I} X^I \to X^I$ and 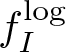 $f_I^{\log}$ restricts to a map
$f_I^{\log}$ restricts to a map  $\pi_I^{\log}\colon \mathsf K_{d,n} \to \mathsf S_{d(\vert I \vert-1)-1}$.
$\pi_I^{\log}\colon \mathsf K_{d,n} \to \mathsf S_{d(\vert I \vert-1)-1}$.
The maps we have described fit together in the following diagram:

The analytification of this diagram is:

Since ![]() $\text{Conf} _n(\mathbb R^{2d})$ is dense in
$\text{Conf} _n(\mathbb R^{2d})$ is dense in ![]() $\text{FM}^\text{top}_n(\mathbb R^{2d})$ and since the blow-down map
$\text{FM}^\text{top}_n(\mathbb R^{2d})$ and since the blow-down map  $\rho_I\colon~\mathrm{Bl}^{\mathbb{R}}_{\Delta_{I}}\ (\mathbb R^{2d})^{I} \to (\mathbb R^{2d})^I$ has an inverse on
$\rho_I\colon~\mathrm{Bl}^{\mathbb{R}}_{\Delta_{I}}\ (\mathbb R^{2d})^{I} \to (\mathbb R^{2d})^I$ has an inverse on ![]() $\text{Conf} _I(\mathbb R^{2d})$ there is only one possible set of maps
$\text{Conf} _I(\mathbb R^{2d})$ there is only one possible set of maps  $(f_I^{\log})^\text{KN}$ and
$(f_I^{\log})^\text{KN}$ and  $(\pi_I^{\log})^\text{KN}$ which can make this diagram commute. By definition, this diagram also commutes if we insert the maps
$(\pi_I^{\log})^\text{KN}$ which can make this diagram commute. By definition, this diagram also commutes if we insert the maps ![]() $f_I, \pi_I$ defined in section 3 and thus we must have
$f_I, \pi_I$ defined in section 3 and thus we must have  $(f_I^{\log})^\text{KN} = f_I$ and
$(f_I^{\log})^\text{KN} = f_I$ and  $(\pi_I^{\log})^\text{KN} = \pi_I$.
$(\pi_I^{\log})^\text{KN} = \pi_I$.
Finally, let  $\pi_i^{\log}$ be the map
$\pi_i^{\log}$ be the map
 \begin{equation*}\pi_i^{\log}\colon \mathsf T_{d,n} \to \mathsf S_0 = (\text{Spec } \mathbb C, 0\colon \mathcal O_{\mathbb{C}}\to \mathcal O_{\mathbb{C}})\end{equation*}
\begin{equation*}\pi_i^{\log}\colon \mathsf T_{d,n} \to \mathsf S_0 = (\text{Spec } \mathbb C, 0\colon \mathcal O_{\mathbb{C}}\to \mathcal O_{\mathbb{C}})\end{equation*}given by the only possible map on the level of schemes and the isomorphism of log structures
 \begin{equation*}(\pi_i^{\log})^* \mathcal O_{\mathbb C} \xrightarrow{\cong} \bigotimes_{i\in S} \mathcal O_{T_{d,n}}(I).\end{equation*}
\begin{equation*}(\pi_i^{\log})^* \mathcal O_{\mathbb C} \xrightarrow{\cong} \bigotimes_{i\in S} \mathcal O_{T_{d,n}}(I).\end{equation*} It is clear that the analytification of this map is the projection map ![]() $\pi_i\colon (S^1)^n\times~\text{K}_{2d,n} \to S^1$ as desired.
$\pi_i\colon (S^1)^n\times~\text{K}_{2d,n} \to S^1$ as desired.
We are now ready to show that the analytifications of the composition and symmetry maps in  $\text{\textbf{CGK}}^{\log}_d$ are the composition and symmetry maps of
$\text{\textbf{CGK}}^{\log}_d$ are the composition and symmetry maps of ![]() $\text{\textbf{FM}}_{2d}\rtimes S^1$. For the symmetry action this is trivial as we can again use that
$\text{\textbf{FM}}_{2d}\rtimes S^1$. For the symmetry action this is trivial as we can again use that ![]() $\text{Conf} _n(\mathbb C^d) \subseteq~\text{FM}^\text{top}_n(\mathbb C^d)$ is dense to conclude this using an argument similar to the one above.
$\text{Conf} _n(\mathbb C^d) \subseteq~\text{FM}^\text{top}_n(\mathbb C^d)$ is dense to conclude this using an argument similar to the one above.
A somewhat more complicated argument is needed to prove that the analytifications of the  $\text{\textbf{CGK}}^{\log}_n$ composition morphisms and
$\text{\textbf{CGK}}^{\log}_n$ composition morphisms and ![]() $\circ_i$-operations are the corresponding maps of the
$\circ_i$-operations are the corresponding maps of the ![]() $\text{\textbf{FM}}_{2d}\rtimes S^1$ operad. We merely give an outline of this argument. First note that for any surjection of finite sets
$\text{\textbf{FM}}_{2d}\rtimes S^1$ operad. We merely give an outline of this argument. First note that for any surjection of finite sets ![]() $\varphi\colon I\twoheadrightarrow J$ the induced map
$\varphi\colon I\twoheadrightarrow J$ the induced map ![]() $(\mathbb A^d)^J \to (\mathbb A^d)^I$ extends uniquely to a map
$(\mathbb A^d)^J \to (\mathbb A^d)^I$ extends uniquely to a map  $\mathrm{Bl}^{\log}_{\Delta_J}(\mathbb A^d)^J \to~\mathrm{Bl}^{\log}_{\Delta_I}(\mathbb A^d)^I$ which restricts to a map
$\mathrm{Bl}^{\log}_{\Delta_J}(\mathbb A^d)^J \to~\mathrm{Bl}^{\log}_{\Delta_I}(\mathbb A^d)^I$ which restricts to a map  $g_\varphi^{\log}\colon \mathsf S_{d(\vert J \vert-1)-1}\to \mathsf S_{d(\vert I \vert-1)-1}$. By the same argument as above the analytification of this map must be the map
$g_\varphi^{\log}\colon \mathsf S_{d(\vert J \vert-1)-1}\to \mathsf S_{d(\vert I \vert-1)-1}$. By the same argument as above the analytification of this map must be the map  $g_\varphi\colon S^{2d(\vert J \vert-1)-1} \to S^{2d(\vert I \vert-1)-1}$ defined in section 3. Using this one can verify that the analytification of
$g_\varphi\colon S^{2d(\vert J \vert-1)-1} \to S^{2d(\vert I \vert-1)-1}$ defined in section 3. Using this one can verify that the analytification of ![]() $\gamma^{\log}$ is the composition morphism of
$\gamma^{\log}$ is the composition morphism of ![]() $\text{\textbf{FM}}_{2d}\rtimes S^1$ componentwise. That is, if
$\text{\textbf{FM}}_{2d}\rtimes S^1$ componentwise. That is, if ![]() $\gamma$ denotes the composition map in
$\gamma$ denotes the composition map in ![]() $\text{\textbf{FM}}_{2d}\rtimes S^1$ we can verify that
$\text{\textbf{FM}}_{2d}\rtimes S^1$ we can verify that
 \begin{equation*}\pi_I \circ \gamma = \pi_I\circ (\gamma^{\log})^\text{KN} = (\pi_I^{\log}\circ\gamma^{\log})^\text{KN}\end{equation*}
\begin{equation*}\pi_I \circ \gamma = \pi_I\circ (\gamma^{\log})^\text{KN} = (\pi_I^{\log}\circ\gamma^{\log})^\text{KN}\end{equation*} for every ![]() $I \subseteq M$ and from this
$I \subseteq M$ and from this ![]() $\gamma = (\gamma^{\log})^\text{KN}$ immediately follows. The
$\gamma = (\gamma^{\log})^\text{KN}$ immediately follows. The ![]() $\circ_i$ case is analogous. We include the proof for one important step which hopefully also provides some insight into the methods used to fill in the remaining steps of the argument.
$\circ_i$ case is analogous. We include the proof for one important step which hopefully also provides some insight into the methods used to fill in the remaining steps of the argument.
Let ![]() $f\colon \mathsf S_0\times \mathsf S_n\to \mathsf S_n$ be the map given by the canonical isomorphism
$f\colon \mathsf S_0\times \mathsf S_n\to \mathsf S_n$ be the map given by the canonical isomorphism ![]() $f\colon~\text{Spec } \mathbb C\times \mathbb P^n\to \mathbb P^n$ on underlying schemes and by the obvious isomorphism
$f\colon~\text{Spec } \mathbb C\times \mathbb P^n\to \mathbb P^n$ on underlying schemes and by the obvious isomorphism  $f^*\mathcal O_{\mathbb P^n}(-1) \xrightarrow{\cong} \pi_1^*\mathcal O_{\text{Spec } \mathbb C}\otimes \pi_2^*\mathcal O_{\mathbb P^n}(-1)$ for the log structures. Here
$f^*\mathcal O_{\mathbb P^n}(-1) \xrightarrow{\cong} \pi_1^*\mathcal O_{\text{Spec } \mathbb C}\otimes \pi_2^*\mathcal O_{\mathbb P^n}(-1)$ for the log structures. Here ![]() $\pi_1,\pi_2$ denote the corresponding projection maps from the product
$\pi_1,\pi_2$ denote the corresponding projection maps from the product ![]() $\text{Spec } \mathbb C \times \mathbb P^n$.
$\text{Spec } \mathbb C \times \mathbb P^n$.
Proposition 5.11. The analytification ![]() $f^\text{KN}\colon S^1\times S^{2n-1} \to S^{2n-1}$ is the
$f^\text{KN}\colon S^1\times S^{2n-1} \to S^{2n-1}$ is the ![]() $S^1\cong~\text{SO}(2)$ action on
$S^1\cong~\text{SO}(2)$ action on ![]() $S^{2n-1}$ induced by the diagonal inclusion
$S^{2n-1}$ induced by the diagonal inclusion ![]() $\text{SO}(2) \hookrightarrow~\text{SO}(2n)$.
$\text{SO}(2) \hookrightarrow~\text{SO}(2n)$.
Proof. First, let ![]() $F\colon \mathbb A^1 \times \mathbb A^n \to \mathbb A^n$ be the map
$F\colon \mathbb A^1 \times \mathbb A^n \to \mathbb A^n$ be the map ![]() $(z,(x_1,\dots, x_n))\mapsto (zx_1,\dots, zx_n)$. By the universal property of the blow-up this induces a map
$(z,(x_1,\dots, x_n))\mapsto (zx_1,\dots, zx_n)$. By the universal property of the blow-up this induces a map  $\tilde F \colon \mathbb A^1\times~\mathrm{Bl}_{p}\ \mathbb A^n \to~\mathrm{Bl}_{p}\ \mathbb A^n$, where
$\tilde F \colon \mathbb A^1\times~\mathrm{Bl}_{p}\ \mathbb A^n \to~\mathrm{Bl}_{p}\ \mathbb A^n$, where ![]() $p$ denotes the origin in
$p$ denotes the origin in ![]() $\mathbb A^n$. Furthermore,
$\mathbb A^n$. Furthermore,  $\tilde F^{-1}(E_p)$, where
$\tilde F^{-1}(E_p)$, where ![]() $E_p$ is the exceptional divisor in
$E_p$ is the exceptional divisor in ![]() $\mathrm{Bl}_{p}\ \mathbb A^n$, is the scheme theoretic union
$\mathrm{Bl}_{p}\ \mathbb A^n$, is the scheme theoretic union ![]() $o\times\mathrm{Bl}_{p}\ \mathbb A^n \cup \mathbb A^1 \times E_p$. By lemma 5.1 this gives a commutative diagram of log varieties:
$o\times\mathrm{Bl}_{p}\ \mathbb A^n \cup \mathbb A^1 \times E_p$. By lemma 5.1 this gives a commutative diagram of log varieties:

where ![]() $\tilde F^{\log}$ denotes the map
$\tilde F^{\log}$ denotes the map ![]() $\tilde F$ extended to a map log varieties in the obvious way and where
$\tilde F$ extended to a map log varieties in the obvious way and where ![]() $i,j$ are the strict morphisms induced by the inclusions of fibres over the origin for the underlying schemes. The analytification of this diagram is of the following form:
$i,j$ are the strict morphisms induced by the inclusions of fibres over the origin for the underlying schemes. The analytification of this diagram is of the following form:

where ![]() $\tilde F' = \tilde F^\text{KN}$ and
$\tilde F' = \tilde F^\text{KN}$ and ![]() $f' = f^\text{KN}$. Since ρ is a homeomorphism on a dense subset there is only one pair
$f' = f^\text{KN}$. Since ρ is a homeomorphism on a dense subset there is only one pair ![]() $f',\tilde F'$ which can make the diagram commute by the same argument as above. It is easy to construct a function
$f',\tilde F'$ which can make the diagram commute by the same argument as above. It is easy to construct a function ![]() $\tilde F'$ such that the diagram commutes with
$\tilde F'$ such that the diagram commutes with ![]() $f$' equal to the group action morphism and from this the lemma follows.
$f$' equal to the group action morphism and from this the lemma follows.
The results of this section taken together give our main theorem.
Theorem 5.12. The Kato–Nakayama analytification of  $\text{\textbf{CGK}}^{\log}_d$ is homeomorphic to
$\text{\textbf{CGK}}^{\log}_d$ is homeomorphic to ![]() $\text{\textbf{FM}}_{2d}\rtimes S^1$.
$\text{\textbf{FM}}_{2d}\rtimes S^1$.
5.4. Virtual log geometric generalizations
We end this article by discussing some apparent generalizations of these results in the category of virtual log schemes. The most immediate improvement we get with virtual morphisms is that, by example 2.8, we there are virtual morphisms
It is not hard to show that we can choose such a morphism such that it satisfies the unit axiom for our operad. Hence, in the category of log schemes with virtual morphisms we can define  $\text{\textbf{CGK}}^{\log}_d$ to be an operad, not just a pseudo-operad. It is clear that theorem 5.12 still holds for this operad.
$\text{\textbf{CGK}}^{\log}_d$ to be an operad, not just a pseudo-operad. It is clear that theorem 5.12 still holds for this operad.
Virtual morphisms also allow us to construct the (unframed) Fulton–MacPherson operad ![]() $\text{\textbf{FM}}_{2d}$ as the analytification of an operad of log schemes with virtual morphisms. Indeed, the operad composition map
$\text{\textbf{FM}}_{2d}$ as the analytification of an operad of log schemes with virtual morphisms. Indeed, the operad composition map
 \begin{equation*}\gamma \colon T_{d,n}\times \prod_{i=1}^n T_{d,q^{-1}(i)} \to T_{d,M}\end{equation*}
\begin{equation*}\gamma \colon T_{d,n}\times \prod_{i=1}^n T_{d,q^{-1}(i)} \to T_{d,M}\end{equation*}extends to a virtual morphism of log schemes
 \begin{equation*}\mathsf K_{d,n}\times \prod_{i=1}^n \mathsf K_{d,q^{-1}(i)} \to \mathsf K_{d,M}.\end{equation*}
\begin{equation*}\mathsf K_{d,n}\times \prod_{i=1}^n \mathsf K_{d,q^{-1}(i)} \to \mathsf K_{d,M}.\end{equation*}This map is defined using lemmas 5.3 and 5.4 but this time we replace the isomorphism in lemma 5.4, (b) with the isomorphism
 \begin{equation*}\gamma^*\mathcal O_{T_{d,M}}(q^{-1}(r)) \xrightarrow{\cong} \left (\bigotimes_{r\in I}\pi_0^* \mathcal O_{T_{d,n}}(I)^{\otimes(-1)}\right ) \otimes \pi_r^* \mathcal O_{d, q^{-1}(r)}(q^{-1}(r)).\end{equation*}
\begin{equation*}\gamma^*\mathcal O_{T_{d,M}}(q^{-1}(r)) \xrightarrow{\cong} \left (\bigotimes_{r\in I}\pi_0^* \mathcal O_{T_{d,n}}(I)^{\otimes(-1)}\right ) \otimes \pi_r^* \mathcal O_{d, q^{-1}(r)}(q^{-1}(r)).\end{equation*} This gives a well defined virtual morphism of log structures by our definitions. These maps define an operad  $\text{\textbf{CGK}}^{\text{V-log}}_d$ in log schemes with virtual morphisms. Using the same methods as before one can show that the analytification of the resulting operad is
$\text{\textbf{CGK}}^{\text{V-log}}_d$ in log schemes with virtual morphisms. Using the same methods as before one can show that the analytification of the resulting operad is ![]() $\text{\textbf{FM}}_{2d}$.
$\text{\textbf{FM}}_{2d}$.
Theorem 5.13. The Kato–Nakayama analytification of  $\text{\textbf{CGK}}^{\text{V-log}}_d$ is homeomorphic to
$\text{\textbf{CGK}}^{\text{V-log}}_d$ is homeomorphic to ![]() $\text{\textbf{FM}}_{2d}$.
$\text{\textbf{FM}}_{2d}$.
Acknowledgements
This article is a reworked version of the authors master’s thesis [Reference Lindström19] and is written as a part of the author’s Ph.D. studies. The author would like to thank his Ph.D supervisor Dan Petersen for many helpful discussions and suggestions both during the writing of this article and the master’s thesis.


















