Hostname: page-component-7dd5485656-glrdx Total loading time: 0 Render date: 2025-10-29T18:36:36.289Z Has data issue: false hasContentIssue false
  • English
  • Français

Normalized positive solutions for Schrödinger equations with potentials in unbounded domains

Part of: Elliptic equations and systems

Published online by Cambridge University Press:  04 September 2023

Sergio Lancelotti  and
Riccardo Molle Open the ORCID record for Riccardo Molle [Opens in a new window]
Sergio Lancelotti
Affiliation:
Dipartimento di Scienze Matematiche, Politecnico di Torino, Corso Duca degli Abruzzi n. 24, 10129 Torino, Italy (sergio.lancelotti@polito.it)
Riccardo Molle
Affiliation:
Dipartimento di Matematica, Università di Roma “Tor Vergata”, Via della Ricerca Scientifica n. 1, 00133 Roma, Italy (molle@mat.uniroma2.it)
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper deals with the existence of positive solutions with prescribed $L^2$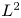 norm for the Schrödinger equation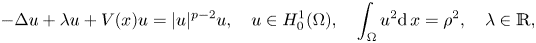

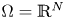$$-\Delta u+\lambda u+V(x)u=|u|^{p-2}u,\quad u\in H^1_0(\Omega),\quad\int_\Omega u^2{\rm d}\,x=\rho^2,\quad\lambda\in\mathbb{R},$$
where $\Omega =\mathbb {R}^N$ or $\mathbb {R}^N\setminus \Omega$ 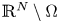is a compact set, $\rho >0$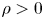, $V\ge 0$ 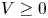(also $V\equiv 0$ 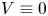is allowed), $p\in (2,2+\frac 4 N)$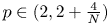. The existence of a positive solution $\bar u$ 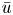is proved when $V$ 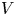verifies a suitable decay assumption (Dρ), or if $\|V\|_{L^q}$ 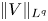is small, for some $q\ge \frac N2$ 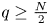($q>1$ 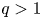if $N=2$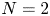). No smallness assumption on $V$ 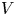is required if the decay assumption (Dρ) is fulfilled. There are no assumptions on the size of $\mathbb {R}^N\setminus \Omega$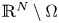. The solution $\bar u$ 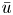is a bound state and no ground state solution exists, up to the autonomous case $V\equiv 0$ 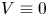and $\Omega =\mathbb {R}^N$.

Keywords

Nonlinear Schrödinger equationsnormalized solutionsexterior domainspositive solutions

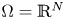MSC classification

Primary: 35J10: Schrödinger operator
Secondary: 35J60: Nonlinear elliptic equations 35J20: Variational methods for second-order elliptic equations

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 154 , Issue 5 , October 2024 , pp. 1518 - 1551
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alves, C. O. and Ji, C.. Normalized solutions for the Schrödinger equations with L2-subcritical growth and different types of potentials. J. Geom. Anal. 32 (2022), 165.CrossRefGoogle Scholar
Ambrosetti, A. and Malchiodi, A., Perturbation methods and semilinear elliptic problems on $R^n$, volume 240 of Progress in Mathematics (Birkhäuser Verlag, Basel, 2006).10.1007/3-7643-7396-2CrossRefGoogle Scholar
Bahri, A. and Li, Y. Y.. On a min-max procedure for the existence of a positive solution for certain scalar field equations in $R^N$. Rev. Mat. Iberoamericana 6 (1990), 1–15.CrossRefGoogle Scholar
Bahri, A. and Lions, P.-L.. On the existence of a positive solution of semilinear elliptic equations in unbounded domains. Ann. Inst. H. Poincaré C Anal. Non Linéaire 14 (1997), 365–413.CrossRefGoogle Scholar
Bartsch, T. and de Valeriola, S.. Normalized solutions of nonlinear Schrödinger equations. Arch. Math. (Basel) 100 (2013), 75–83.CrossRefGoogle Scholar
Bartsch, T., Molle, R., Rizzi, M. and Verzini, G.. Normalized solutions of mass supercritical Schrödinger equations with potential. Comm. Partial Differ. Equ. 46 (2021), 1729–1756.10.1080/03605302.2021.1893747CrossRefGoogle Scholar
Benci, V. and Cerami, G.. Positive solutions of some nonlinear elliptic problems in exterior domains. Arch. Rational Mech. Anal. 99 (1987), 283–300.10.1007/BF00282048CrossRefGoogle Scholar
Berestycki, H. and Lions, P.-L.. Nonlinear scalar field equations. I. Existence of a ground state. Arch. Rational Mech. Anal. 82 (1983), 313–345.CrossRefGoogle Scholar
Cazenave, T., Semilinear Schrödinger equations, volume 10 of Courant Lecture Notes in Mathematics (New York University, Courant Institute of Mathematical Sciences, New York; American Mathematical Society, Providence, RI, 2003).Google Scholar
Cazenave, T. and Lions, P.-L.. Orbital stability of standing waves for some nonlinear Schrödinger equations. Comm. Math. Phys. 85 (1982), 549–561.CrossRefGoogle Scholar
Cerami, G.. Some nonlinear elliptic problems in unbounded domains. Milan J. Math. 74 (2006), 47–77.10.1007/s00032-006-0059-zCrossRefGoogle Scholar
Cerami, G. and Molle, R.. On some Schrödinger equations with non regular potential at infinity. Discrete Contin. Dyn. Syst. 28 (2010), 827–844.CrossRefGoogle Scholar
Cerami, G. and Molle, R.. Positive bound state solutions for some Schrödinger-Poisson systems. Nonlinearity 29 (2016), 3103–3119.CrossRefGoogle Scholar
Cerami, G. and Passaseo, D.. Existence and multiplicity results for semilinear elliptic Dirichlet problems in exterior domains. Nonlinear Anal. 24 (1995), 1533–1547.10.1016/0362-546X(94)00116-YCrossRefGoogle Scholar
Cerami, G. and Passaseo, D.. The effect of concentrating potentials in some singularly perturbed problems. Calc. Var. Partial Differ. Equ. 17 (2003), 257–281.CrossRefGoogle Scholar
Devillanova, G. and Solimini, S.. The role of planar symmetry and of symmetry constraints in the proof of existence of solutions to some scalar field equations. Nonlinear Anal. 201 (2020), 112060.10.1016/j.na.2020.112060CrossRefGoogle Scholar
Dovetta, S., Serra, E. and Tilli, P.. Action versus energy ground states in nonlinear Schrödinger equations. Math. Ann. 385 (2023), 1545–1576.CrossRefGoogle Scholar
Ekeland, I.. On the variational principle. J. Math. Anal. Appl. 47 (1974), 324–353.CrossRefGoogle Scholar
Esteban, M. J. and Lions, P.-L.. Existence and nonexistence results for semilinear elliptic problems in unbounded domains. Proc. Roy. Soc. Edinburgh Sect. A 93 (1982/83), 1–14.10.1017/S0308210500031607CrossRefGoogle Scholar
Esteban, M. J. and Lions, P.-L.. Existence and nonexistence results for semilinear elliptic problems in unbounded domains. Proc. Roy. Soc. Edinburgh Sect. A 93 (1982/83), 1–14.10.1017/S0308210500031607CrossRefGoogle Scholar
Ghoussoub, N., Duality and perturbation methods in critical point theory, volume 107 of Cambridge Tracts in Mathematics (Cambridge University Press, Cambridge, 1993). With appendices by David Robinson.10.1017/CBO9780511551703CrossRefGoogle Scholar
Gidas, B., Ni, W. M. and Nirenberg, L., Symmetry of positive solutions of nonlinear elliptic equations in $R^n$. In Mathematical Analysis and Applications, Part A, volume 7 of Adv. in Math. Suppl. Stud. (Academic Press, New York-London, 1981), pp. 369–402.Google Scholar
Gilbarg, D. and Trudinger, N. S., Elliptic Partial Differential Equations of Second Order. Classics in Mathematics (Springer-Verlag, Berlin, 2001). Reprint of the 1998 edition.CrossRefGoogle Scholar
Ikoma, N. and Miyamoto, Y.. Stable standing waves of nonlinear Schrödinger equations with potentials and general nonlinearities. Calc. Var. Partial Differ. Eq. 59 (2020), 48.CrossRefGoogle Scholar
Jeanjean, L.. Existence of solutions with prescribed norm for semilinear elliptic equations. Nonlinear Anal. 28 (1997), 1633–1659.CrossRefGoogle Scholar
Jeanjean, L. and Lu, S.-S.. Nonradial normalized solutions for nonlinear scalar field equations. Nonlinearity 32 (2019), 4942–4966.CrossRefGoogle Scholar
Kwong, M. K.. Uniqueness of positive solutions of $\Delta u-u+u^p=0$ in $R^n$. Arch. Rational Mech. Anal. 105 (1989), 243–266.10.1007/BF00251502CrossRefGoogle Scholar
Lancelotti, S. and Molle, R.. Positive solutions for autonomous and non-autonomous nonlinear critical elliptic problems in unbounded domains. NoDEA Nonlinear Differ. Equ. Appl. 27 (2020), 8.CrossRefGoogle Scholar
Leoni, G., A first course in Sobolev spaces, volume 181 of Graduate Studies in Mathematics 2nd edition (American Mathematical Society, Providence, RI, 2017).CrossRefGoogle Scholar
Lieb, E. H. and Loss, M., Analysis, volume 14 of Graduate Studies in Mathematics. 2nd ed (American Mathematical Society, Providence, RI, 2001).10.1090/gsm/014CrossRefGoogle Scholar
Molle, R., Musso, M. and Passaseo, D.. Positive solutions for a class of nonlinear elliptic problems in $\mathbf {R}^N$. Proc. Roy. Soc. Edinburgh Sect. A 130 (2000), 141–166.CrossRefGoogle Scholar
Molle, R. and Passaseo, D.. On the behaviour of the solutions for a class of nonlinear elliptic problems in exterior domains. Discrete Contin. Dynam. Systems 4 (1998), 445–454.10.3934/dcds.1998.4.445CrossRefGoogle Scholar
Molle, R. and Passaseo, D.. Infinitely many positive solutions of nonlinear Schrödinger equations. Calc. Var. Partial Differ. Equ. 60 (2021), 79.CrossRefGoogle Scholar
Molle, R., Riey, G. and Verzini, G.. Normalized solutions to mass supercritical Schrödinger equations with negative potential. J. Differ. Equ. 333 (2022), 302–331.10.1016/j.jde.2022.06.012CrossRefGoogle Scholar
Noris, B., Tavares, H. and Verzini, G.. Existence and orbital stability of the ground states with prescribed mass for the $L^2$-critical and supercritical NLS on bounded domains. Anal. PDE 7 (2014), 1807–1838.CrossRefGoogle Scholar
Pucci, P. and Serrin, J., The maximum principle, volume 73 of Progress in Nonlinear Differential Equations and their Applications (Birkhäuser Verlag, Basel, 2007).10.1007/978-3-7643-8145-5CrossRefGoogle Scholar
Song, L.. Existence and orbital stability/instability of standing waves with prescribed mass for the $l^2$-supercritical nls in bounded domains and exterior domains. Calc. Var. Partial. Differ. Equ. 62 (2023), 176.CrossRefGoogle Scholar
Strauss, W. A.. Existence of solitary waves in higher dimensions. Comm. Math. Phys. 55 (1977), 149–162.CrossRefGoogle Scholar
Struwe, M., Variational methods, Vol. 34, 4th ed (Springer-Verlag, Berlin, 2008). Applications to nonlinear partial differential equations and Hamiltonian systems.Google Scholar
Yang, Z., Qi, S. and Zou, W.. Normalized solutions of nonlinear Schrödinger equations with potentials and non-autonomous nonlinearities. J. Geom. Anal. 32 (2022), 159.CrossRefGoogle Scholar
Zhang, Z. and Zhang, Z.. Normalized solutions of mass subcritical Schrödinger equations in exterior domains. NoDEA Nonlinear Differ. Eq. Appl. 29 (2022), 32.10.1007/s00030-022-00764-5CrossRefGoogle Scholar