Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Abdulla, Ugur G.
and
King, John R.
2000.
Interface Development and Local Solutions to Reaction-Diffusion Equations.
SIAM Journal on Mathematical Analysis,
Vol. 32,
Issue. 2,
p.
235.
Abdulla, Ugur G.
2002.
Evolution of interfaces and explicit asymptotics at infinity for the fast diffusion equation with absorption.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 50,
Issue. 4,
p.
541.
da Silva, João Vitor
Ochoa, Pablo
and
Silva, Analia
2018.
Regularity for degenerate evolution equations with strong absorption.
Journal of Differential Equations,
Vol. 264,
Issue. 12,
p.
7270.
Diaz, Jesus Ildefonso
Hilhorst, Danielle
and
Kyriazopoulos, Paris
2021.
parabolic system with strong absorption modeling dry-land vegetation.
Electronic Journal of Differential Equations,
Vol. 2021,
Issue. 01-104,
p.
08.
Aal-Rkhais, Habeeb A.
and
Qasim, Ruba H.
2021.
The Development of interfaces in a Parabolic p-Laplacian type diffusion equation with weak convection.
Journal of Physics: Conference Series,
Vol. 1963,
Issue. 1,
p.
012105.

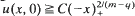 with
with 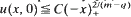 with C<C
with C<C