Hostname: page-component-65f69f4695-tzd6m Total loading time: 0 Render date: 2025-06-30T19:11:38.062Z Has data issue: false hasContentIssue false
  • English
  • Français

On the L∞-maximization of the solution of Poisson's equation: Brezis–Gallouet–Wainger type inequalities and applications

Part of: Elliptic equations and systems Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  20 February 2020

Davit Harutyunyan  and
Hayk Mikayelyan
Davit Harutyunyan
Affiliation:
Department of Mathematics, University of California, Santa Barbara, CA93106-3080, USA (harutyunyan@ucsb.edu)
Hayk Mikayelyan
Affiliation:
School of Mathematical Sciences, University of Nottingham Ningbo, 199 Taikang East Road, Ningbo315100, PR China (Hayk.Mikayelyan@nottingham.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

For the solution of the Poisson problem with an L∞ right hand side

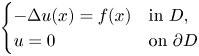\begin{cases} -\Delta u(x) = f (x) & {\rm in}\ D, \\ u=0 & {\rm on}\ \partial D \end{cases}
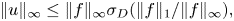we derive an optimal estimate of the form
\|u\|_\infty\leq \|f\|_\infty \sigma_D(\|f\|_1/\|f\|_\infty),
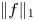 where σD is a modulus of continuity defined in the interval [0, |D|] and depends only on the domain D. The inequality is optimal for any domain D and for any values of $\|f\|_1$ and 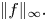$\|f\|_\infty .$ We also show that
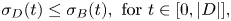\sigma_D(t)\leq\sigma_B(t),\text{ for }t\in[0,|D|],
 where B is a ball and |B| = |D|. Using this optimality property of σD, we derive Brezis–Galloute–Wainger type inequalities on the L∞ norm of u in terms of the L1 and L∞ norms of f. As an application we derive L∞ − L1 estimates on the k-th Laplace eigenfunction of the domain D.

Keywords

Optimal rearrangementsBrezis–Gallouet–Wainger inequalityBathtub principleLaplace eigenfunctions

MSC classification

Primary: 35R11: Fractional partial differential equations
Secondary: 35J60: Nonlinear elliptic equations

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 1 , February 2021 , pp. 79 - 92
Check for updates
Copyright
Copyright © The Author(s) 2020. Published by The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1Brezis, H. and Gallouet, T.. Nonlinear Schrödinger evolution equations. Nonlinear Anal. Theory Methods Appl. 4 (1980), 677–681.CrossRefGoogle Scholar
2Brezis, H. and Wainger, S.. A note on limiting cases of Sobolev embedding and convolution inequalities. Commun. Partial Differ. Equ. 5 (1987), 773–789.CrossRefGoogle Scholar
3Elliott, L. H. and Loss, M.. Analysis. Graduate Studies in Mathematics, vol. 14 (Providence, RI: American Mathematical Society, second edition, 2001).Google Scholar
4Engler, H.. An alternative proof of the Brezis—Wainger inequality. Commun. Partial Differ. Equ. 14 (1989), 541–544.Google Scholar
5Foias, C., Manley, O., Rosa, R. and Temam, R.. Navier-Stokes Equations and Turbulence (Cambridge: Cambridge University Press, 2001). ISBN 0-521-36032-3.CrossRefGoogle Scholar
6Gilbarg, D. and Trudinger, N. S.. Elliptic Partial Differential Equations of Second Order (Berlin-Heidelberg-New York-Tokyo: Springer-Verlag, 1983). XIII, 513 S. DM 128. ISBN 3-540-13025-X (Grundlehren der mathematischen Wissenschaften 224).Google Scholar
7Giga, M. H., Giga, Y. and Saal, J.. Nonlinear partial differential equations. Asymptotic behaviour of solutions and self-similar solutions. Progress in Nonlinear Differential Equations and Their Applications, vol. 79, ISBN: 978-0-8176-4173-3 (Boston, MA: Birkhäuser, Boston, Ltd., 2010).Google Scholar
8Górka, P.. Brezis–Waigner inequality in Riemannian manifolds. J. Inequal. Appl. 11 (2008), 1–6. Article ID 715961.CrossRefGoogle Scholar
9Kato, T. and Ponce, G.. Commutator estimates and the Euler and Navier–Stokes equations. Commun. Pure Appl. Math. 41 (1988), 891–907.CrossRefGoogle Scholar
10Kresin, G. and Maz'ya, V.. Maximum principles and sharp constants for solutions of elliptic and parabolic systems. Mathematical Surveys and Monographs, Vol. 183, pp. viii+317, ISBN: 978-0-8218-8981-7 (Providence, RI: American Mathematical Society, 2012).CrossRefGoogle Scholar
11Maz'ya, V. and Shaposhnikova, T.. Brézis–Gallouet–Wainger type inequality for irregular domains. Complex Variables and Elliptic Equations 56 (2011) 10–11, 991–1002. A tribute to Victor I. Burenkov; Guest Editors: Robert P. Gilbert, Massimo Lanza de Cristoforis and Alexander Pankov.CrossRefGoogle Scholar
12Morii, K., Sato, T. and Wadade, H.. Brézis–Gallouet–Wainger type inequality with a double logarithmic term in the Hölder space: Its sharp constants and extremal functions. Nonlinear Anal.: Theory Methods Appl. 73 (2010), 1747–1766.CrossRefGoogle Scholar
13Morii, K., Sato, T., Sawano, Y. and Wadade, H.. Sharp constants of Brézis–Gallout–Wainger type inequalities with a double logarithmic term on bounded domains in Besov and Triebel-Lizorkin spaces. Boundary Value Prob. (2010), 1–38. ID:584521.Google Scholar
14Sawano, Y.. Brezis–Gallouet–Wainger type inequality for Besov-Morrey spaces. Studia Math. 196 (2010), 91–101.CrossRefGoogle Scholar
15Talenti, G.. Elliptic equations and rearrangements. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 3 (1976), 697–718.Google Scholar
16Vishik, M.. Incompressible flows of an ideal liquid with unbounded vorticity. Commun. Math. Phys. 213 (2000), 697–731.CrossRefGoogle Scholar
17Weinberger, H. F.. Symmetrization in uniformly elliptic problems. In 1962 Studies in Mathematical Analysis and Related Topics, pp. 424–428 (Stanford, California: Stanford Univ. Press, 1962).Google Scholar