Hostname: page-component-76fb5796d-5g6vh Total loading time: 0 Render date: 2024-04-29T15:26:45.869Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Sobolev stability threshold for shear flows near Couette in 2D MHD equations

Part of: Hydrodynamic stability

Published online by Cambridge University Press:  12 February 2024

Ting Chen  and
Ruizhao Zi
Ting Chen
Affiliation:
School of Mathematics and Statistics, Central China Normal University, Wuhan, 430079, P. R. China (1255193542@qq.com)
Ruizhao Zi
Affiliation:
School of Mathematics and Statistics, and Key Laboratory of Nonlinear Analysis & Applications (Ministry of Education), Central China Normal University, Wuhan, 430079, P. R. China (rzz@ccnu.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work, we study the Sobolev stability of shear flows near Couette in the 2D incompressible magnetohydrodynamics (MHD) equations with background magnetic field $(\alpha,0 )^\top$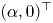 on $\mathbb {T}\times \mathbb {R}$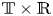. More precisely, for sufficiently large $\alpha$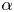, we show that when the initial datum of the shear flow satisfies $\left \| U(y)-y\right \|_{H^{N+6}}\ll 1$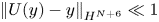, with $N>1$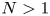, and the initial perturbations ${u}_{\mathrm {in}}$ 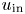and ${b}_{\mathrm {in}}$ 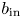satisfy $\left \| ( {u}_{\mathrm {in}},{b}_{\mathrm {in}}) \right \| _{H^{N+1}}=\epsilon \ll \nu ^{\frac 56+\tilde \delta }$ 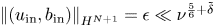for any fixed $\tilde \delta >0$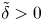, then the solution of the 2D MHD equations remains $\nu ^{-(\frac {1}{3}+\frac {\tilde \delta }{2})}\epsilon$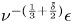-close to $( e^{\nu t \partial _{yy}}U(y),0)^\top$ 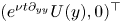for all $t>0$.

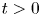Keywords

MHD equationsCouette flowstability

MSC classification

Primary: 76E05: Parallel shear flows
Secondary: 76E25: Stability and instability of magnetohydrodynamic and electrohydrodynamic flows
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 51
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonelli, P., Dolce, M. and Marcati, P., Linear stability analysis for 2d shear flows near Couette in the isentropic compressible euler equations, preprint arXiv:2003.01694, (2020).Google Scholar
Bardos, C., Sulem, C. and Sulem, P.-L.. Longtime dynamics of a conductive fluid in the presence of a strong magnetic field. Trans. Am. Math. Soc. 305 (1988), 175–191.Google Scholar
Bedrossian, J., Germain, P. and Masmoudi, N.. On the stability threshold for the 3D Couette flow in Sobolev regularity. Ann. Math. 185 (2017), 541–608.Google Scholar
Bedrossian, J., Germain, P. and Masmoudi, N.. Dynamics near the subcritical transition of the 3D Couette flow I: Below threshold case. Mem. Amer. Math. Soc. 266 (2020), v+158.Google Scholar
Bedrossian, J., Germain, P. and Masmoudi, N.. Dynamics near the subcritical transition of the 3D Couette flow II: Above threshold case. Mem. Amer. Math. Soc. 279 (2022), 135.Google Scholar
Bedrossian, J. and Masmoudi, N.. Inviscid damping and the asymptotic stability of planar shear flows in the 2D Euler equations. Publ. Math. Inst. Hautes Études Sci. 122 (2015), 195–300.CrossRefGoogle Scholar
Bedrossian, J., Masmoudi, N. and Vicol, V.. Enhanced dissipation and inviscid damping in the inviscid limit of the Navier–Stokes equations near the 2D Couette flow. Arch. Ration. Mech. Anal. 216 (2016), 1087–1159.Google Scholar
Bedrossian, J., Vicol, V. and Wang, F.. The Sobolev stability threshold for 2D shear flows near Couette. J. Nonlinear. Sci. 28 (2018), 2051–2075.CrossRefGoogle Scholar
Cai, Y. and Lei, Z.. Global well-posedness of the incompressible magnetohydrodynamics. Arch. Ration. Mech. Anal. 228 (2018), 969–993.Google Scholar
Case, K. M.. Stability of inviscid plane Couette flow. Phys. Fluids 3 (1960), 143–148.Google Scholar
Chandrasekhar, S.. The stability of viscous flow between rotating cylinders in the presence of a magnetic field. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 216 (1953), 293–309.Google Scholar
Chen, Q., Li, T., Wei, D. and Zhang, Z.. Transition threshold for the 2-D Couette flow in a finite channel. Arch. Ration. Mech. Anal. 238 (2020), 125–183.CrossRefGoogle Scholar
Chen, X. and Morrison, P. J.. A sufficient condition for the ideal instability of shear flow with parallel magnetic field. Physics of Fluids B: Plasma Phys. 3 (1991), 863–865.Google Scholar
Chen, Q., Wei, D. Y. and Zhang, Z., Transition threshold for the 3D Couette flow in a finite channel. arXiv:2006.00721 (2020).Google Scholar
Chen, Q., Wei, D. and Zhang, Z.. Linear inviscid damping and enhanced dissipation for monotone shear flows. Comm. Math. Phys. 400 (2023), 215–276.Google Scholar
Chen, Q., Wei, D., Zhang, P. and Zhang, Z., Nonlinear inviscid damping for 2-D inhomogeneous incompressible Euler equations, arXiv:2303.14858 (2023).Google Scholar
Davidson, P. A., An Introduction to Magnetohydrodynamics, Cambridge Texts in Applied Mathematics (Cambridge University Press, Cambridge, 2001).Google Scholar
Deng, Y. and Masmoudi, N., Long-time instability of the couette flow in low gevrey spaces. Comm. Pure Appl. Math. 2023).Google Scholar
He, L., Xu, L., Li, and Yu, P.. On global dynamics of three dimensional magnetohydrodynamics: nonlinear stability of Alfvén waves. Ann. PDE 4 (2018), 105.Google Scholar
Hirota, M., Tatsuno, T. and Yoshida, Z.. Resonance between continuous spectra: secular behavior of Alfvén waves in a flowing plasma. Phys. Plasmas 12 (2005), 012107.CrossRefGoogle Scholar
Inci, H., Kappeler, T. and Topalov, P.. On the regularity of the composition of diffeomorphism. Mem. Amer. Math. Soc. 226 (2013), 1–64.Google Scholar
Ionescu, A. D. and Jia, H.. Inviscid damping near the Couette flow in a channel. Comm. Math. Phys. 374 (2020), 2015–2096.Google Scholar
Ionescu, A. D. and Jia, H., Nonlinear inviscid damping near monotonic shear flows. arXiv:2001.03087, 2020, to appear in Acta Math.Google Scholar
Ionescu, A. D., Iyer, S. and Jia, H., Linear inviscid damping and vorticity depletion for non-monotonic shear flows. arXiv:2301.00288 (2023).Google Scholar
Jia, H.. Linear inviscid damping in Gevrey spaces. Arch. Ration. Mech. Anal. 235 (2020), 1327–1355.Google Scholar
Jia, H.. Linear inviscid damping near monotone shear flows. SIAM J. Math. Anal. 52 (2020), 623–652.Google Scholar
Kelvin, L.. Stability of fluid motion-rectilinear motion of viscous fluid between two parallel plates. Philos Mag. 24 (1887), 188.Google Scholar
Knobel, N. and Zillinger, C.. On echoes in magnetohydrodynamics with magnetic dissipation. arXiv:2301.06935 (2023).Google Scholar
Li, H., Masmoudi, N. and Zhao, W., Asymptotic stability of two-dimensional Couette flow in a viscous fluid, arXiv:2208.14898v1 (2022).Google Scholar
Lifschitz, A.. Magnetohydrodynamics and Spectral Theory (Kluwer Academic Publishers, Dordrecht, 1989).Google Scholar
Liss, K.. On the Sobolev stability threshold of 3D Couette flow in a uniform magnetic field. Commun. Math. Phys. 377 (2020), 859–908.Google Scholar
Liu, H., Masmoudi, N., Zhai, C. and Zhao, W.. Linear damping and depletion in flowing plasma with strong sheared magnetic fields. J. Math. Pures Appl. 158 (2022), 1–41.Google Scholar
Masmoudi, N. and Zhao, W.. Nonlinear inviscid damping for a class of monotone shear flows in finite channel. arXiv preprint arXiv: 2001. 08564 (2020).Google Scholar
Masmoudi, N. and Zhao, W.. Stability threshold of the 2D Couette flow in Sobolev spaces. Ann. Inst. H. Poincaré C Anal. Non Linéaire 39 (2022), 245–325.Google Scholar
Orr, W.. The stability or instability of steady motions of a perfect liquid and of a viscous liquid, Part I: a perfect liquid. Proc. R. Ir. Acad., A Math. Phys. Sci. 27 (1907), 9–68.Google Scholar
Reynolds, O.. An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Proc. R. Soc. Lond. 35 (1883), 84.Google Scholar
Ren, S., Wei, D. and Zhang, Z.. Long time behavior of Alfvén waves in flowing plasma: the destruction of magnetic island. SIAM J. Math. Anal. 53 (2021), 5548–5579.Google Scholar
Ren, S. and Zhao, W.. Linear damping of Alfvén waves by phase mixing. SIAM J. Math. Anal. 49 (2017), 2101–2137.Google Scholar
Schmid, P. J. and Henningson, D. S.. Stability and Transition in Shear Flows, Vol. 142 (Berlin: Springer, 2001).Google Scholar
Shivamoggi, B. K. and Debnath, L.. Stability of magnetohydrodynamic stratified shear flows. Acta Mech. 68 (1987), 33–42.Google Scholar
Tataronis, J. and Grossmann, W.. Decay of MHD wave by phase mixing I. The sheet-pinch in plane geometry. Z. Physik 261 (1973), 203–216.Google Scholar
Velikhov, E. P.. Stability of an ideally conducting liquid flowing between rotating cylinders in a magnetic field, Zhur. Eksptl. i Teoret. Fiz. 36 (1959), 1398–1404. (Russian); translated as Soviet Physics JETP, 9(1959), 995–998.Google Scholar
Wei, D. and Zhang, Z.. Global well-posedness of the MHD equations in a homogeneous magnetic field. Anal. PDE 10 (2017), 1361–1406.Google Scholar
Wei, D. and Zhang, Z.. Transition threshold for the 3D Couette flow in Sobolev space. Comm. Pure Appl. Math. 74 (2021), 2398–2479.Google Scholar
Wei, D., Zhang, Z. and Zhao, W.. Linear inviscid damping for a class of monotone shear flow in Sobolev spaces. Comm. Pure Appl. Math. 71 (2018), 617–687.Google Scholar
Wei, D., Zhang, Z. and Zhao, W.. Linear inviscid damping and vorticity depletion for shear flows. Ann. PDE 5 (2019), 101.Google Scholar
Wei, D., Zhang, Z. and Zhao, W.. Linear inviscid damping and enhanced dissipation for the Kolmogorov flow. Adv. Math. 362 (2020), 106963.Google Scholar
Yaglom, A. M.. Hydrodynamic Instability and Transition to Turbulence, Vol. 100 (Berlin: Springer, 2012).CrossRefGoogle Scholar
Zhai, C., Zhang, Z. and Zhao, W.. Long-time behavior of Alfvén waves in a flowing plasma: generation of the magnetic island. Arch. Ration. Mech. Anal. 242 (2021), 1317–1394.Google Scholar
Zhang, Z. and Zi, R.. Stability threshold of Couette flow for 2D Boussinesq equations in Sobolev spaces. J. Math. Pures Appl. 179 (2023), 123–182.Google Scholar
Zhao, W.. Inviscid damping of monotone shear flows for 2D inhomogeneous Euler equation with non-constant density in a finite channel. arXiv:2304.09841 (2023).Google Scholar
Zillinger, C.. Linear inviscid damping for monotone shear flows. Trans. Amer. Math. Soc. 369 (2017), 8799–8855.Google Scholar