Hostname: page-component-6bb9c88b65-bcq64 Total loading time: 0 Render date: 2025-07-25T06:41:24.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Regularity results for minimizers of non-autonomous integral functionals

Part of: Miscellaneous topics in calculus of variations and optimal control Elliptic equations and systems

Published online by Cambridge University Press:  25 July 2025

Antonio Giuseppe Grimaldi  and
Stefania Russo
Antonio Giuseppe Grimaldi*
Affiliation:
Dipartimento di Ingegneria, Università degli Studi di Napoli “Parthenope”, Centro Direzionale Isola C4, Napoli, 80143, Italy (antoniogiuseppe.grimaldi@collaboratore.uniparthenope.it)
Stefania Russo
Affiliation:
Dipartimento di Matematica e Applicazioni “R. Caccioppoli”, Università degli Studi di Napoli “Federico II”, Via Cintia, Napoli, 80126, Italy (stefania.russo3@unina.it)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish the higher fractional differentiability for the minimizers of non-autonomous integral functionals of the form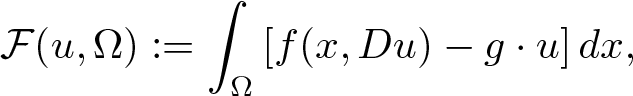

\begin{align*}\mathcal{F}(u,\Omega):=\int_\Omega \left[ f(x,Du)- g \cdot u \right] dx ,\end{align*}

under (p, q)-growth conditions. Besides a suitable differentiability assumption on the partial map $x \mapsto D_\xi f(x,\xi)$, we do not need to assume any differentiability assumption on the function g.

Keywords

Local minimizernon-standard growthhigher differentiabilityBesov spacesnon-unifom ellipticity

MSC classification

Primary: 49N60: Regularity of solutions
Secondary: 35J87: Nonlinear elliptic unilateral problems and nonlinear elliptic variational inequalities

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 28
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Baisón, A. L., Clop, A., Giova, R., Orbitg, J. and Passarelli di Napoli, A.. Fractional differentiability for solutions of nonlinear elliptic equations. Potential Anal. 46 (2017), 403–430.10.1007/s11118-016-9585-7CrossRefGoogle Scholar
Baisón, A. L., Clop, A. and Orobitg, J., Beltrami equations with coefficient in the fractional Sobolev space $W^{2,\frac{2}{\theta}}$, Proc. Amer. Math. Soc. 145 (2017), 1, 139–149.10.1090/proc/13204CrossRefGoogle Scholar
Baroni, P., Colombo, M. and Mingione, G.. Regularity for general functionals with double phase. Calc. Var. PDE. 57 (2018), 62.10.1007/s00526-018-1332-zCrossRefGoogle Scholar
Bergh, J. and Löfström, J.. Interpolation spaces, An introduction. (Springer-Verlag, Berlin Heidelberg New York, 1976).10.1007/978-3-642-66451-9CrossRefGoogle Scholar
Clop, A., Faraco, D. and Ruiz, A.. Stability of Calderón’s inverse conductivity problem in the plane for discontinuous conductivities. Inverse Probl. Imaging. 4 (2010), 49–91.10.3934/ipi.2010.4.49CrossRefGoogle Scholar
Clop, A., Giova, R. and Passarelli di Napoli, A.. Besov regularity for solutions of p-harmonic equations. Adv. Nonlinear Anal. 8 (2019), 762–778.10.1515/anona-2017-0030CrossRefGoogle Scholar
Cruz, V., Mateu, J. and Orobitg, J.. Beltrami equation with coefficient in Sobolev and Besov spaces. Canad. J. Math. 65 (2013), 1217–1235.10.4153/CJM-2013-001-7CrossRefGoogle Scholar
De Filippis, C. and Mingione, G., Nonuniformly elliptic Schauder theory. Invent. math. 234 (2023), 1109–1196.10.1007/s00222-023-01216-2CrossRefGoogle Scholar
De Filippis, C. and Mingione, G.. The sharp growth rate in nonuniformly elliptic. Schauder theory, preprint arXiv:2401.07160v2.Google Scholar
Eleuteri, M. and Passarelli di Napoli, A.. Higher differentiability for solutions to a class of obstacle problems. Calc. Var. 57 (2018), 115.10.1007/s00526-018-1387-xCrossRefGoogle Scholar
Eleuteri, M. and Passarelli di Napoli, A.. Regularity results for a class of non-differentiable obstacle problems. Nonlinear Analysis. 194 (2020), 111434.10.1016/j.na.2019.01.024CrossRefGoogle Scholar
Esposito, L., Leonetti, F. and Mingione, G.. Sharp regularity for functionals with (p, q) growth. J. Differ. Equ. 204 (2004), 5–55.10.1016/j.jde.2003.11.007CrossRefGoogle Scholar
Fonseca, I, Maly, J. and Mingione, G.. Scalar minimizers with fractal singular sets. Arch. Ration. Mech. Anal. 172 (2004), 295–307.10.1007/s00205-003-0301-6CrossRefGoogle Scholar
Gavioli, C.. Higher differentiability of solutions to a class of obstacle problems under non-standard growth conditions. Forum Math. 31 (2019), 1501–1516.10.1515/forum-2019-0148CrossRefGoogle Scholar
Gavioli, C.. A priori estimates for solutions to a class of obstacle problems under (p, q)-growth conditions. Journal of Elliptic and Parabolic Equations. 5 (2019), 325–347.10.1007/s41808-019-00043-yCrossRefGoogle Scholar
Gentile, A.. Higher differentiability results for solutions to a class of non-autonomous obstacle problems with sub-quadratic growth conditions. Forum Mathematicum. 33 (2021), 669–695.10.1515/forum-2020-0299CrossRefGoogle Scholar
Giaquinta, M.. Growth conditions and regularity, a counterexample. Manuscripta Math. 59 (1987), 245–248.10.1007/BF01158049CrossRefGoogle Scholar
Giova, R.. Higher differentiability for n-harmonic systems with Sobolev coefficients. J. Diff. Equ. 259 5667–5687.10.1016/j.jde.2015.07.004CrossRefGoogle Scholar
Giova, R. and Passarelli di Napoli, A.. Regularity results for a priori bounded minimizers of non-autonomous functionals with discontinuous coefficients. Adv. Calc. Var. 12 (2019), 85–110.10.1515/acv-2016-0059CrossRefGoogle Scholar
Giusti, E.. Direct methods in the calculus of variations. World scientific publishing Co., Singapore. (2003).10.1142/5002CrossRefGoogle Scholar
Grimaldi, A. G.. Regularity results for solutions to a class of obstacle problems. Nonlinear Analysis: Real World Applications. 62 (2021), 103377.Google Scholar
Grimaldi, A. G. and Ipocoana, E.. Higher differentiability results in the scale of Besov spaces to a class of double-phase obstacle problems. ESAIM: COCV. 28 (2022), 51.Google Scholar
Grimaldi, A. G. and Ipocoana, E.. Higher fractional differentiability for solutions to a class of obstacle problems with non-standard growth conditions. Advances in Calculus of Variations. 16 (2023), 935–960.10.1515/acv-2021-0074CrossRefGoogle Scholar
Grimaldi, A. G., and Ipocoana, E. (2024). Regularity results for Hölder minimizers to functionals with non-standard growth. Math. Nachr 297 (8), 3143–3164.10.1002/mana.202300412CrossRefGoogle Scholar
Hamburger, C.. Regularity of differential forms minimizing degenerate elliptic functionals. J. Reine Angew. Math. 431 (1992), 7–64.Google Scholar
Haroske, D.. Envelopes and sharp embeddings of function spaces. Chapman and Hall CRC, Boca Raton. (2006).Google Scholar
Koskela, P., Yang, D. and Zhou, Y.. Pointwise characterizations of Besov and Triebel-Lizorkin spaces and quasiconformal mappings. Adv. Math. 226 (2011), 3579–3621.10.1016/j.aim.2010.10.020CrossRefGoogle Scholar
Kristensen, J. and Mingione, G.. Boundary regularity in variational problems. Arch. Ration. Mech. Anal. 198 (2010), 369–455.10.1007/s00205-010-0294-xCrossRefGoogle Scholar
Marcellini, P.. Regularity of minimizers of integrals of the calculus of variations with non standard growth conditions. Arch. Rational Mech. Anal. 105 (1989), 267–284.10.1007/BF00251503CrossRefGoogle Scholar
Marcellini, P.. Regularity and existence of solutions of elliptic equations with (p, q)-growth conditions. J. Differential Equations. 90 (1991), 1–30.10.1016/0022-0396(91)90158-6CrossRefGoogle Scholar
Marcellini, P.. Regularity for elliptic equations with general growth conditions. J. Differential Equations. 105 (1993), 296–333.10.1006/jdeq.1993.1091CrossRefGoogle Scholar
Mingione, G. and Radulescu, V.. Recent developments in problems with nonstandard growth and nonuniform ellipticity Journal of Mathematical Analysis and Applications. 501 (2021), 125–197.10.1016/j.jmaa.2021.125197CrossRefGoogle Scholar
Passarelli di Napoli, A.. Higher differentiability of minimizers of variational integrals with sobolev coefficients. Adv. Calc. Var. 7 (2014), 59–89.10.1515/acv-2012-0006CrossRefGoogle Scholar
Passarelli di Napoli, A.. Higher differentiability of solutions of elliptic systems with Sobolev coefficients: The case $p = n =2$. Pot. Anal. 41 (2014), 715–735.10.1007/s11118-014-9390-0CrossRefGoogle Scholar
Russo, S.. Higher Differentiability of Minimizers for Non-Autonomous Orthotropic Functionals, Nonlinear Analysis: Real World Applications, 87 (2026) 104450.Google Scholar
Triebel, H.. Theory of Function Spaces. Monogr. Math., Vol. 78, Birkhäuser, Basel, 1983.Google Scholar
Zhikov, V. V.. Averaging of functionals of the calculus of variations and elasticity theory. Izv. Akad. Nauk SSSR Ser. Mat. 50 (1986), 675–710.Google Scholar
Zhikov, V. V.. On some variational problems. Russ. J. Math. Phys. 5 (1997), 105–116.Google Scholar