Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Carrillo, José
and
Wittbold, Petra
1999.
Uniqueness of Renormalized Solutions of Degenerate Elliptic–Parabolic Problems.
Journal of Differential Equations,
Vol. 156,
Issue. 1,
p.
93.
Porretta, Alessio
1999.
Existence results for nonlinear parabolic equations via strong convergence of truncations.
Annali di Matematica Pura ed Applicata,
Vol. 177,
Issue. 1,
p.
143.
Fontes, Magnus
2000.
A Monotone operator method for elliptic—parabolic equations.
Communications in Partial Differential Equations,
Vol. 25,
Issue. 3-4,
p.
681.
Andreu, F.
Ballester, C.
Caselles, V.
and
Mazón, J.M.
2001.
The Dirichlet Problem for the Total Variation Flow.
Journal of Functional Analysis,
Vol. 180,
Issue. 2,
p.
347.
Blanchard, Dominique
Murat, François
and
Redwane, Hicham
2001.
Existence and Uniqueness of a Renormalized Solution for a Fairly General Class of Nonlinear Parabolic Problems.
Journal of Differential Equations,
Vol. 177,
Issue. 2,
p.
331.
Villani, Cédric
2002.
Vol. 1,
Issue. ,
p.
141.
Villani, Cédric
2002.
Vol. 1,
Issue. ,
p.
189.
Carrillo, Jose
and
Wittbold, Petra
2002.
Renormalized Entropy Solutions of Scalar Conservation Laws with Boundary Condition.
Journal of Differential Equations,
Vol. 185,
Issue. 1,
p.
137.
Alexandre, R.
and
Villani, C.
2002.
On the Boltzmann equation for long‐range interactions.
Communications on Pure and Applied Mathematics,
Vol. 55,
Issue. 1,
p.
30.
Villani, Cédric
2002.
Vol. 1,
Issue. ,
p.
75.
Villani, Cédric
2002.
Vol. 1,
Issue. ,
p.
263.
Villani, Cédric
2002.
Vol. 1,
Issue. ,
p.
245.
García Vázquez, Concepción
and
Ortegón Gallego, Francisco
2003.
An Elliptic Equation with Blowing-Up Diffusion and Data in L1: Existence and Uniqueness.
Mathematical Models and Methods in Applied Sciences,
Vol. 13,
Issue. 09,
p.
1351.
Kobayasi, Kazuo
2003.
The equivalence of weak solutions and entropy solutions of nonlinear degenerate second-order equations.
Journal of Differential Equations,
Vol. 189,
Issue. 2,
p.
383.
Bendahmane, M.
and
Saad, M.
2003.
A predator–prey system with L1 data.
Journal of Mathematical Analysis and Applications,
Vol. 277,
Issue. 1,
p.
272.
Droniou, Jérôme
Porretta, Alessio
and
Prignet, Alain
2003.
Parabolic Capacity and Soft Measures for Nonlinear Equations.
Potential Analysis,
Vol. 19,
Issue. 2,
p.
99.
Zimmer, Johannes
2004.
Global existence for a nonlinear system in thermoviscoelasticity with nonconvex energy.
Journal of Mathematical Analysis and Applications,
Vol. 292,
Issue. 2,
p.
589.
Jakubowski, Volker G.
and
Wittbold, Petra
2004.
On a nonlinear elliptic–parabolic integro-differential equation with L1-data.
Journal of Differential Equations,
Vol. 197,
Issue. 2,
p.
427.
Montesinos, María Teresa González
and
Gallego, Francisco Ortegón
2005.
Renormalized Solutions to a Nonlinear Parabolic-Elliptic System.
SIAM Journal on Mathematical Analysis,
Vol. 36,
Issue. 6,
p.
1991.
Andreu, Fuensanta
Caselles, Vicent
and
Mazón, José M.
2005.
A Strongly Degenerate Quasilinear Equation: the Parabolic Case.
Archive for Rational Mechanics and Analysis,
Vol. 176,
Issue. 3,
p.
415.

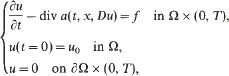
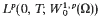 into its dual space. The renormalised solution is an element of
into its dual space. The renormalised solution is an element of 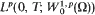 with
with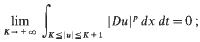
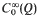 and where
and where